基于元认知理论的中考数学复习课实践研究—-“一题一课”简约课堂的教学尝试

广东省东莞市中堂镇实验中学

众所周知,中考数学复习课对学生系统地学好数学,发展思维能力,是极为重要的,对提高教学质量也是不可或缺的环节.复习课不像新授课一样有每节课的具体教学内容和任务,久而久之复习课便形成一套思维定势:概念、定理回忆、例题精讲、练习、测试反馈,这样会使学生感到枯燥无味从而影响复习效率.日前,依然存在不少教师在初三数学复习课的教学中,只注重学习的结果分数,而不是获得知识的过程.在解题教学中,教师常常讲的是自己的思维结果、即解题的思路是什么,怎样作铺助线,怎样推理得到结论,或是根据什么公式、法则计算,计算中要注意什么等等,很少讲自己分析寻找思路的过程,在分析、研究过程中走过什么弯路或是碰过壁,如何修正、调整的.其实,教师的这种经验对于学生来说,比得到这问题的解更加重要.

元认知理论是由弗拉维尔于20世纪70年代提出,元认知就是个体关于自己的认知过程的知识和调节的能力.当学生的元认知水平较高,他们就能有效地监控调节自己的数学学习行为,促进学习效率的提高,因此适当了解学生数学学习的元认知水平,对于数学教学的有效开展,并有针对性地指导学生的数学学习有重要的指导意义.研究发现:在数学思维活动中,思维监控系统处于支配地位,是数学思维活动的监控室.在元认知思想的指导下,即使思维受阻停滞,也能及时矫正思维方向,调整思维的策略,把思维活动拉回正轨,起到“北斗导航”精准带路的作用.我们老师平时上课都会依据自己的经验,提出一些很有价值的问题,但是很多学生并不能快速内化吸收,因而我们会发现刚刚学会的问题学生很快就忘记了,感觉学生从不曾留下深刻足迹.“一题一课”可很好地解决这个问题,利用问题变式反复追问,不仅记忆深刻烙下深刻痕迹,而且使学生思维更有系统性.下面我以“中考第二轮复习回归课本研读一题一课系列之——相似”一课为例来谈谈我的一点思考.

1 原题呈现,源自课本

题目源自人教版课本九下数学58页拓广探索的第11题,内容如下:

题目如图1,一块材料的形状是锐角三角形ABC,边BC =120 mm,高AD =80mm.把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB,AC 上,这个正方形零件的边长是多少?

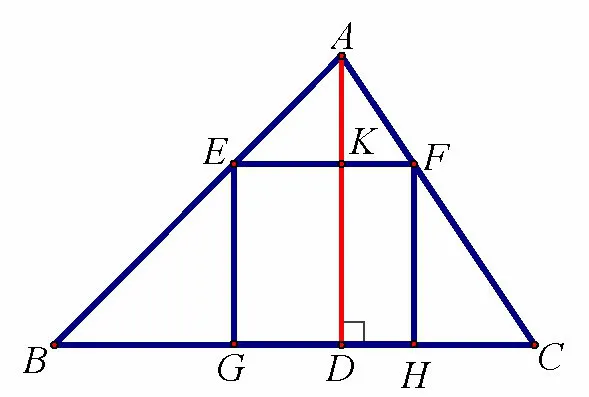
图1

首先利用课件PPT 呈现该题目,由学生说题,“说已知,说结论,说出已知可得的信息和结论”.需要的条件,说出已知与问题之间的联系.所谓说已知,说结论,即为说出已知条件是什么,有什么用处;说出结论是怎样的,要得到结论需要什么条件.而说出相关知识点及相似题型就避免了天马行空,使思维范围就大大缩小了.若有学生需要适当提示时,不要直接给出方法,要引导学生自己去思考.

师:正方形有哪些性质呢?

生1:四条边相等,四个角都是直角,对边互相平行.

师(追问):在三角形内有平行你想到了什么?

生1:两三角形相似.

师:题目知道哪些量?

生2:三角形的一边和一高.

师:相似三角形的性质里有没有涉及到边和高的?

生2:相似三角形对应边的比的对应高的比.

师:生2 讲得太好了,可是这ΔAEF的边和高都不知道,而这边EF 也就是题目要求解的,怎么办呢?

生3:它们之间有联系,可利用方程思想解决！

师:漂亮！马上动笔书写,5分钟后同学们成果展示.

设计意图回归课本,从教材的一道复习题出发,低起点,高立意,可激发学生探究兴趣.引导学生逐步揭示问题的本质,并挖掘隐藏的数量关系,再次巩固相似三角形对应高的比等于对应边的比的性质,了解该性质的用法.关注学生,启发学生,让解法自然生成.答题如下:

解设正方形零件的边长为x mm,则KD = EF =x,AK =80-x,因为EF//BC,所以ΔAEF ∽ΔABC,所以AD⊥BC,所以即解得x=48.

答:正方形零件的边长为48mm.

2 反思原题,自然过渡

再读原题,通过“图形确定性”分析法可知,这个正方形是确定的,确定就是唯一,唯一即是可求！那么,这个正方形零件面积是可求的,那这块三角形材料是否最大限度地使用了? 图形被唯一了,要变化面积需弱化条件,那么自然就把正方形弱化成矩形.

探索1 如果原题中所要加工的零件只是一个矩形,如下图2,问这个矩形的最大面积是多少?

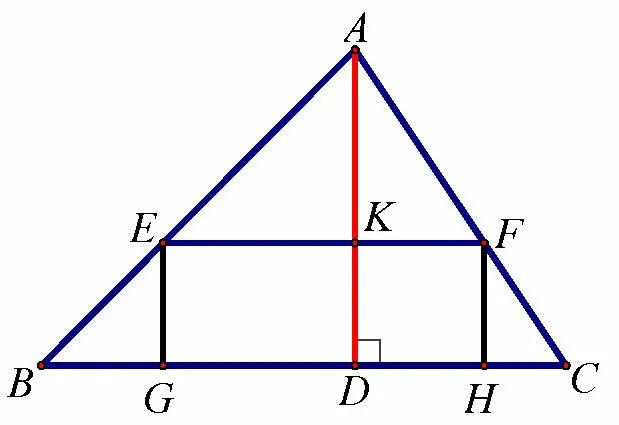
图2

审题可知,这矩形面积是随着EF的长度变化而变化的,则要求它的最大面积,先把面积表示出来,我们知道线段EF 与EG的乘积即为面积.

师:同学们在思考表示面积时有什么困惑吗?

生1:两条线段的长度都不知道,设一条线段为x,另一条又要设y的话,再加上面积S 就共有3个未知数了.

师:这两条线段之间有没有联系呢?

生2:前面的学习知道,可用方程思想来求解第二条线段的表示！

师:很好！那设哪一条线段为x 呢?

生2:都可以.

师:好的,同学们,实践出真知,请马上尝试解决一下.

接着学生分别尝试设EF 与EG为x 时的情况:

结果呈现,对比发现,情况二可直接写出AK的表达式,运算量比情况一少一点,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答即可,答案略.现矩形的两条边长都可表示出来了,若题目修改成问该矩形的周长与边的函数关系式也一样就解决了.剪切掉了矩形剩下三个三角形,我们也可如此设计问题:

探索2当EG 长度为多少时,ΔAEF的面积等于ΔBEG 与ΔCFH 之和?

有了前面的探究基础,这一问就相对容易解决,接下来就是引导学生表示出这三个三角形的面积,在表示ΔBEG与ΔCFH的面积的时候,单独表示发现多了参数BG 与CH,但是面积和时就变成从而可列出方程求解.

3 刨根问底,寻求本质

我们研究问题往往从特殊到一般化的探究思路,若是这块三角形材料的边BC =a,高AD =h.则矩形PQMN面积的最大值是多少呢? 也就是说把原来的数据120 与80分别换成a 与h,也就是说只要知道这个三角形的一边和该边上的高,矩形面积的最大值就是固定的呢? 因解法思路上是相通一致的,从而可求.

探索3 若边BC = a,高AD = h,则矩形PQMN面积的最大值是多少? (用含a,h的代数式表示.)

简解设EG=x,则解得所以所以当时,面积有最大值,

感悟观察结果我们可发现,一个给出一边和这边上的高的三角形,剪切出如上所述的矩形的最大面积就是该三角形面积的一半,而此时边EF 恰为三角形的中位线.而这一结论的得出,我们教师要适时地引导学生进行解后反思,归纳总结,升华思想.

4 拓展应用,融会贯通

有了上面这一般化的结论,如果就停止了前进的步伐的话就太可惜了,这样感觉功亏一篑.要想把这节课的知识达成目标真正落实,还需要及时的二次反馈这一环节步骤.题目可设计如下:

探索4如图3,现有一块四边形的木板余料ABCD,经测量AB= 60 cm,BC= 100cm,CD= 70 cm,且∠B= ∠C= 60°,木匠杨师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.

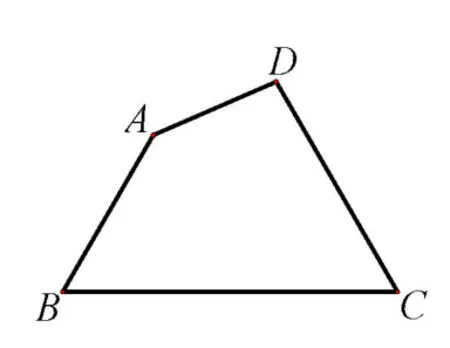
图3

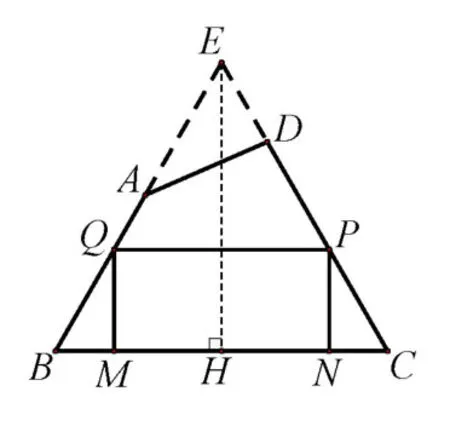
图4

如果是直接拿出这道题目来做的话,难度就很大了.但有了前面的学习,这题就相对容易,但是要让学生自行找到两者的关联,教师在必要时引导提醒学生.给足学生思考的时间,充分暴露思维的全过程,出声思维让思维可视化,这样教师就可以作精准的诊断,而不是学生简单说一句不会,老师就全盘告诉学生答案是什么,导致学生只知道原来是这样做的,不知道为什么这样做.

师:同学们,在解答过程中有哪些困惑吗?

生1:这个是四边形,和前面的不一样.

师:真的不一样吗? 能否联系起来呢?

生2:延长BA和CD,补充完整三角形,就联系起来了.

师:很好！马上动笔试试.

简解如图4,延长BA,CD交于点E,过点E作EH⊥BC于点H,因为∠B= ∠C,所以EB=EC,因为BC= 100,且EH=BC= 50,所以100,因为AE= 40,ED= 30,所以BE,CE的中点Q,P在线段AB,CD上,所以中位线PQ的两端点在线段AB,CD上,由前面的学习可知,矩形PQMN的最大面积为

反思为什么要先判断中位线PQ的两端点在AB、CD上呢? 因为前面的学习我们知道矩形取得最大面积时PQ恰为三角形的中位线,这是要检验取最值时的点存在在原图的线段上,若在虚线AE,DE上就不满足了.

问题解决后,学生自然会获得很大的成就感,从而再次激发了学生的学习兴趣,提升了学生的自我效能感.这里其实渗透了转化与化归的思想,在教学中渗透的基本思想,是学习数学知识的灵魂和精髓,是对数学问题的本质反映.教师在教学过程中不单是要“授人以鱼和授人以渔”,而且是要“授人以欲”,这是价值观对方法论的超越.所谓“欲”,就是根植于内心的理想、信念和为之而努力的激情,它时刻影响着人的行为.我们的大脑不是一个被填充的容器,而是一把需要被点燃的火把.一个掌握方法的人若没有一个积极追求精进的态度,他的方法也是毫无用处的.若是教学目标重点是转向面积类问题的函数表示的话,可以作如下设计:

探索5如图5,已知锐角ΔABC中,边BC= 8,高AD= 10,两动点M,N分别在边AB,AC上滑动,且MN//BC,以MN为边向下作正方形MPQN,设正方形的边长为x.

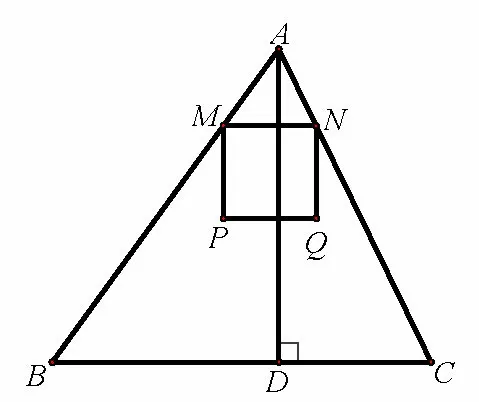
图5

(1)若正方形MPQN的顶点P,Q在边BC上,求MN的长;

(2)设正方形MPQN与ΔABC公共部分的面积为y,当x是多少时,公共部分的面积y最大,最大值是多少?

点评这题目就把前面加工成正方形和矩形的问题统一起来了,而且更系统完善.审题可知,这题考查到了分类讨论思想,它的公共部分分三种情况,在三角形内部、一边在BC上,正方形一部分在三角形的外部,而显然在内部的面积比刚好在边上时要小,所以比较后两种情形时的面积大小即可,不过在取面积二次函数最值时,对应的x要在取值范围内,如若不然就要根据函数的单调性来处理了,此题答案略.

若是教学目标重点是转向相似三角形线段比的等量变换问题的话,可以作如下设计:

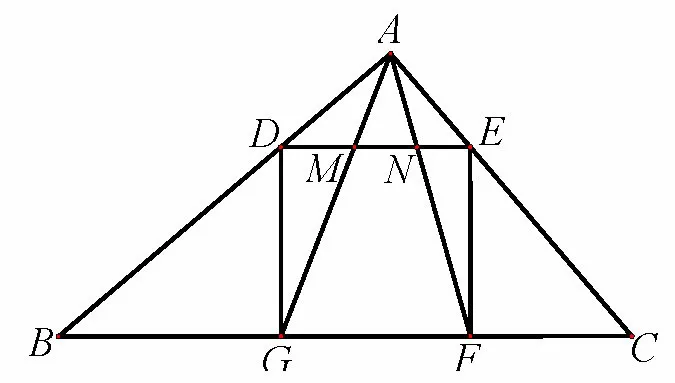
图6

探索6如图6,ΔABC中,∠BAC= 90°,正方形的一边GF在BC上,其余两个顶点D,E分别在AB,AC上.连接AG,AF分别交DE于M,N两点.

(1)求证:

(2)求证:MN2=DM ·EN.

(3)若AB=AC=4,求MN的长.

分析第1问的这类比例证明学生都知道用三角形相似来解决,但是它不属于直接利用一对相似三角形相似就能解决的问题.它需要两对相似,要利用这个来“搭桥过河”,因为那两对比值都与相等;在第2问中除了应用DE//BC,得到还得应用∠BAC= 90°和正方形的性质来推出ΔBGD∽ΔEFC,从而有再由DG=GF=EF推出即可; 有了前两问的结论第3问就较简单了,这里不再赘述.

如果是跳出向下作特殊四边形思路的话,可作如下设计:

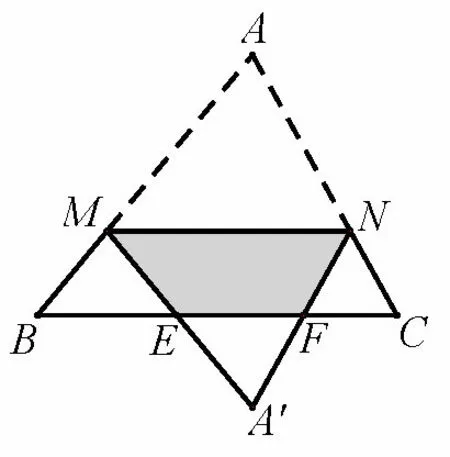
图7

探索7如图7,已知三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C 都为锐角,M为AB 边上一动点(M与点A,B 不重合),过点M作MN//BC,交AC于点N.将ΔAMN 沿MN 折叠,使点A落在BC的下方,设MN = x,ΔA′MN 与四边形BCNM重叠部分面积为y.

(1)试求出y 关于x的函数关系式,并写出自变量x的取值范围;

(2)当x为何值时,重叠部分的面积y最大,最大值是多少?

后话教师示范分析典型的数学例题,引导学生在简单模仿、反复训练、自发领悟的基础上,增加一个“自觉分析”的环节,解题后进行再思考,及时分析自己的解题过程,反思、联系、归纳,并考虑能否进一步归类引伸.题目获解后,回过头来进行解题过程的分析,正是“学会解题”的最好机会,通过解题过程的分析而学会解题,就是积极主动地去发展元认知能力.在解题过程中,对每个问题进行分析时,教师应引导学生,使注意力从指向问题本身转变为指向他们在分析问题时正在做什么、想什么,即是使学生始终监控调节自己的行为,清楚地了解自己思考问题的过程.

“一题一课”让课堂教学从形式上走向了简约,通过有意识地训练提高学生的数学元认知能力,就是提高他对自己学习过程的自我意识,从而增强学习的自觉性,及时调整和改进学习过程,这对学习效率和学习能力的提高是非常关键的.一题一课就是想达成“做一题,得一法,会一类,通一片”的教学目标,从而增强学生的数学核心素养.

总之,增强学生的数学元认知能力,不但让学生知道应该如何思维,更让学生学会如何时刻监控自己的思维,在思维受阻时可及时调整策略.学生是学习的主体,是学习的建构者,让学生学会如何思考,化被动为主动,不断提升学生主动探求的愿望和能力,我们的教育就会充满生机和活力.