初中数学概念教学中的问题与策略—-从广东省中考方向看数学概念教学

广东省佛山市顺德区龙江外国语学校

近五年广东省中考数学试卷紧扣考试大纲,能立足基础,着眼能力,加强数学概念及实际运用的考查,体现了数学新课程倡导的学习方式、教学方式和评价方式,有很强的导向作用,但从学生的卷面作答情况看,成绩不太理想,基础不扎实,知识条理混乱,作答不严谨,应变能力差,我经过反复研究近年广东省中考数学试题,发现广东省试题非常重视数学概念的理解及应用,而往往概念教学是我们教师最易忽略的一个过程.

教师们的培训越来越多,更多的是理论和通识性培训,数学专业技能的培训则少得多;课堂教学改革推动了学生的自主学习,但是在数学教学中弱化数学概念教学的趋势愈发严重,很多教师的概念教学课堂上仅仅是在学生自学的基础上的梳理和简单应用.殊不知,概念教学是数学教学的根本,数学概念是数学知识大厦的地基,基础不牢地动山摇！结合近五年广东省中考题,笔者谈谈概念教学时出现的问题及应该采取的策略.

1 出现的问题

1.1 忽视概念的生成过程

在学习新内容时,往往将一个新的概念直接给出来,让学生记住就这么一回事,其实这种概念教学是非常传统的教学,学生不但记不住,反而打击了创造性,没有真正理解数学知识,以后解题谈不上灵活应用.

例1(2016年广东省中考第2题)如图所示,a与b的大小关系是()

A.a ＜bB.a ＞bC.a=bD.b=2a

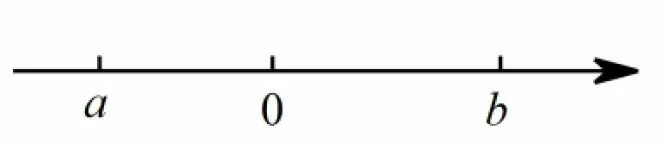
图1

这题属于容易的题目,但如果学生不清楚实数和数轴概念的话,就容易失分,有学生不分正负,将a,b表示的数搞错了,这反映出我们平时教学没有理解实数与数轴的概念.

例2(2017年广东省中考第13题)已知实数a,b在数轴上的对应点的位置如图所示,则a+b____0(填“＞”,“＜”或“=”)

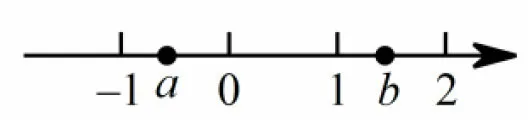
图2

这题是考查数轴与列代数式的概念,这要求我们平时要重视数轴的概念教学.

例3(广东省2017年第3题)已知∠A=70°,则∠A的补角为()

A.110°B.70°C.30°D.20°

这题是单纯考补角知识点,但教师在课堂上讲课时明白告诉学生补角的含义,而没有教补角的形成过程,因此时间一长,学生就容易和余角混淆了.

1.2 忽视概念间的相互联系许多本来有联系的概念,没有将它们串成线、连成片、结成网,概念间形成不了系统,学生解题时就不会有快速的思考,甚至会出现知识间的错误.

例4如图3,把其中的一个小正方形看成是基本图形,这个图形中不包含的变换的是()

图3

A.对称 B.平移 C.相似(相似比不为1)D.旋转

这道题考了图形变换知识点,难度应该不大,但教师如果在教学中没有将这几种变换让学生体会比较,没有总结比较这几种变换的异同点的话,就容易造成失分.

1.3 忽视概念的综合应用

在碰到综合题目时,学生往往是因为读不懂题,理解不了题意而没能将题目解答出来.

例5(广东省2018年中考第16题)如图4,已知等边ΔOA1B1,顶点A1在双曲线上,点B1的坐标为(2,0).过B1作B1A2//OA1交双曲线于点A2,过A2作A2B2//A1B1交x轴于点B2,得到第二个等边ΔB1A2B2; 过B2作B2A3//B1A2交双曲线于点A3,过A3作A3B3//A2B2交x轴于点B3,得到第三个等边ΔB2A3B3;以此类推,···,则点B6的坐标为___

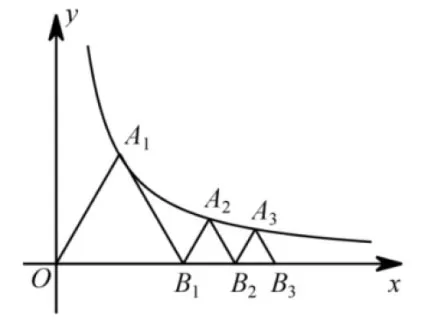
图4

从学生得分情况看,这题得分率较低,很多平时成绩较好的学生对这题也无所适从.当然,这题有一定的难度,首先,学生读不懂题,不知题目讲什么,其次,就算读懂了题目,想不到解题思路,不知道考什么知识点.只因教师平时没有创造条件,让学生在解决实际问题时灵活应用.

广东省近几年中考题目,如果老师不改变课堂模式,不注重概念教学,一味让学生钻入题海,事实证明是不利于学生能力的培养,不利于学生创造性的培养,也很难适应目前中考要求.

2 采取的策略

2.1 让探索的主动权交给学生,把“教”建立在“学”之中

还记得教研室专家远老师对我校进行了教学备考指导,听了我的一节新授课“弧长及扇形的面积”,当时我的教学流程是这样的:

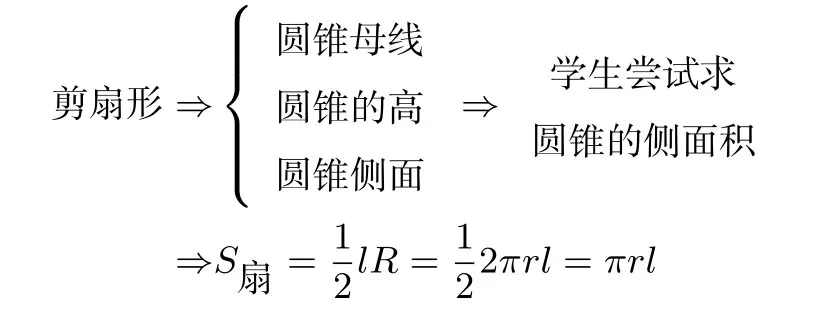
当学生动笔做练习时,好多学生根本代入公式都不懂,更不要说灵活应用了.听课后,远老师说了他的思路:

远老师处理方式的妙处明显使学生“活”起来了,学生是主动获得新知,而不是被动接受,当学生在探索过程中就对新知的形成过程有了深刻的理解和体会,做题也就水到渠成了.他的点评,让我恍然大悟,原来传统教学包办了学生探讨环节,忽视了概念的形成教学,如果教师包办学生的自主性,学生必然能力低下,不能适应中考试题.

2.2 让学生理解概念之间的联系

任何新知的形成都不是单一的,它必然要借助之前的知识,这就要求老师要作为一个引导者,引导学生将各类概念之间联系起来.如扇形面积的推导,一定要结合圆面积公式,因为圆面积是学生记得最牢的S圆=πr2,将圆分成360 份,每一份的面积怎么求呢? 学生自然会想到如果是n°的扇形呢? 学生很快就推出了公式

知识概念之间的联系非常重要,当学生忘了这一概念,他也能通过自身的能力回忆起另一个概念,当出现要区别各类型的概念的题目时,学生也能顺利答对,理解清楚各概念关系时,也不用进行大量重复的练习,学生只要做适量的题目就能掌握知识.大量重复的题目只能僵化学生思维,不利学生发展,也不利能力提升,跟中考方向相违背的.

2.3 概念的应用,要从模仿、变形上升到合情推理、创造

学生学习数学,不能简单停留在理解和掌握知识的层面上,必须学会运用,只有这样,才能真正实现数学价值.但是在运用概念过程中,不能重复机械模仿和简单变换,要进行合情合理的推理和创造.所选取的题目,要典型,要体现初中数学思想,比如转化思想,分类讨论思想,数型结合思想,方程思想等,必要时要进行变式练习.对概念的深刻理解,是提高解题能力的基础,应注重应用,加深理解,培养数学综合能力.

综上所述,数学概念是反映世界的空间形式和数量关系本质属性的思维形式,是数学知识的基础,是数学教材结构最基本的要素,是数学思想和方法的载体.作为一名数学教师,平时要重视数学概念教学,要让学生充分体验知识的形成过程,正确理解数学概念,理解数学公式、公理、定理、定义等,学生才能够利用所学知识解决应际问题,才能适应中考方向,才有利于学生成材.