基于滑模控制的分数阶神经网络的准一致同步性

陈茜瑶，张 海，马俊风

（安庆师范大学数学与计算科学学院，安徽安庆246133）

分数阶微积分是由分数阶导数和分数阶积分两部分组成。分数阶微分系统是一个非常有前景的研究课题，动力学分析、稳定性分析及控制理论都已成为热门的研究课题[1-7]。虽然经典控制方法广泛运用于工业上，但是因非线性系统的控制性能和控制方法不完善，所以经典控制方法并不理想，而滑模控制（SMC）可以保证具有不确定性的非线性系统的稳定性和鲁棒性[8-11]。文献[12]推导出基于忆阻器的具有时滞的分数阶神经网络的准一致同步性判据。文献[13]根据分数阶Lyapunov稳定性判据、线性矩阵不等式及Laplace变换，得出下列具有全/欠驱动的分数阶神经网络基于滑模控制的同步性：

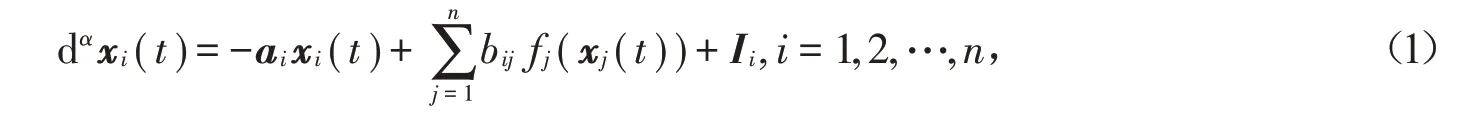
其中分数阶阶数α ∈(0,1)，对于非线性函数fj(xj(t))，n表示神经网络单元数，bij是在第i神经元中第j神经元的常数连接权重，xi(t)是t时刻第i单元的状态，ai为当第i神经元与网络未连接时，重置其电位至静态的速率，Ii为外部输入。

受文献[12-13]启发，本文利用分数阶微分方程、Volterra-integral等式和不等式技巧，讨论基于滑模控制的分数阶神经网络的准一致同步问题，推广了文献[12-13]中的相应结果。将(1)式作为驱动系统，令x(t)=[x1(t),x2(t),…,xn(t)]T，A=diag(a1,a2,…,an)，I=[I1,I2,…,In]T，B=(bij)n×n，则驱动系统(1)可表为

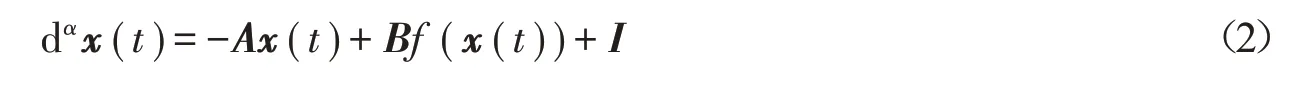
1 预备知识

为了更好地描述相关模型，这里给出相关重要的定义和引理。

定义1[2]对于函数f (t)∈C[[0,+∞),ℝ]，且α ＞0，则称d-α的α阶分数阶积分，其中Γ(α)=e-ttα-1dt。

定义2[2]对于在[0,+∞)上的所有n 阶连续可微函数的集合函数f (t)∈Cn+1[[0,+∞),ℝ]，则Caputo型分数阶导数表示为其中α ＞0，n 为一个正整数，且n-1＜α ＜n，特别有，当0 ＜α ＜1时，有

引理1[7]如果f (t)∈Cn[0,∞)，t ∈[0,T]且n-1＜α ＜n，n ∈ℤ+,则（i）d-αd-βf (t)=d-(α+β)f (t)，α，β ≥0；（ii）dαd-βf (t)=f (t)，α=β ≥0；（iii）d-αdβf (t)=f (t)-(0)，α=β ≥0。

为了考虑分数阶神经网络的准一致同步性，其响应系统为

其中G为控制增益矩阵，且为未知的。

同步误差为e(t)=x(t)-y(t)，则误差系统为定义3[12]对误差系统(4)，如果对∀ε ＞0，存在两个常数0 ＜δ ＜ε，T ＞0，当‖ ‖e(t0) ＜δ 时，有‖ ‖e(t) ＜ε，对∀t ∈J=[t0,t0+T]，其中t0为初始观测时间，则称分数阶神经网络的驱动系统（2）和响应系统(3)能实现准一致同步。

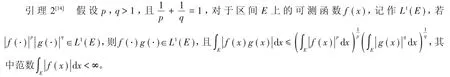
引理3[15]若x ≥-1，0 ＜α ＜1，则(1+x)α≤1+αx。

引理4[16]令z(t),a(t)和h(t)为ℝ+上的非负连续函数，又令1≤p ＜∞为一实数，若

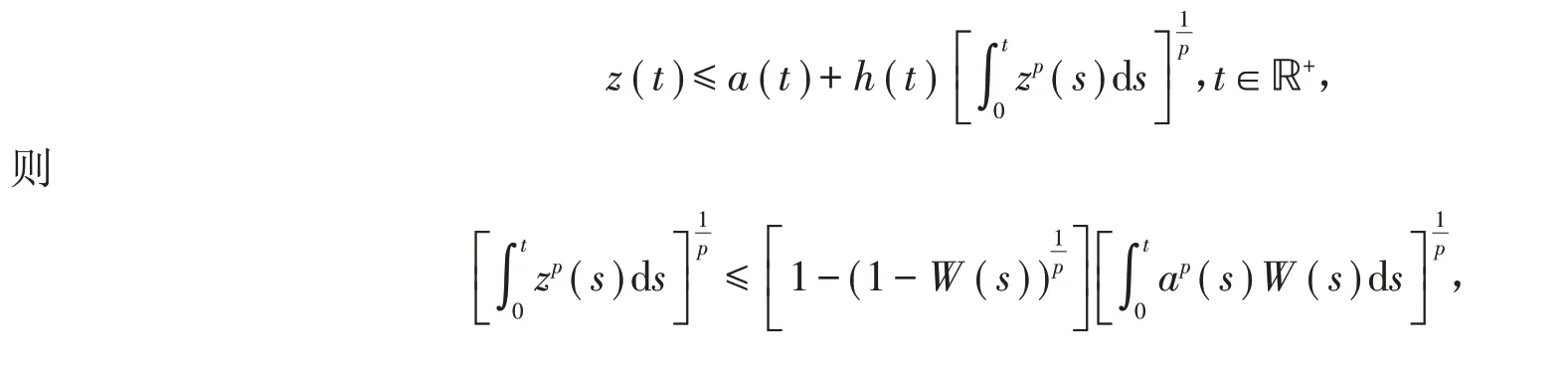
假设（H1）函数fj(·)满足Lipschitz条件，即对于所有的x，y ∈ℝ，存在正标量Fj，则

其中F=diag(F1,F2,…,Fn)。

2 主要结果

文献[13]设计出一个新的分数阶滑模表面，定义为

其中H ∈ℝm×n和G ∈ℝn×m是两个实矩阵，则HG为非奇异，K ∈ℝn×m为常数矩阵。

根据引理1可知，所提出的滑模表面(5)式的分数阶动力学方程定义为

若f (x(t))和f (y(t))是预先已知的，并且令dασ(t)=0，则等价控制信号ueq为

则滑动运动方程为

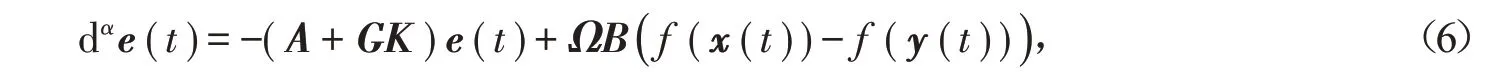
其中Ω=I-G(HG)-1H。

引理5[13]对于给定的Lipschitz常数l= ‖ ‖F ，如果存在一个正定的n×n增益矩阵E和一个m×n增益矩阵K，满足

则动力学方程(6)式是渐近稳定的，且Λ=-PA-AP-PGK -KTGTP。

根据引理1，可得

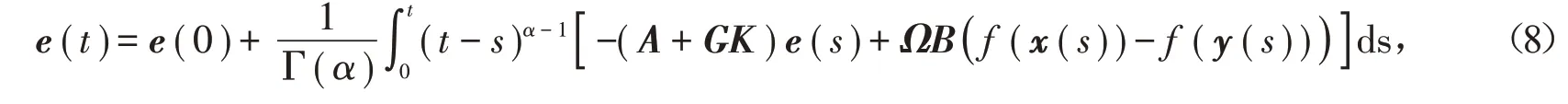
通过对(8)式运用假设(H1)，可得

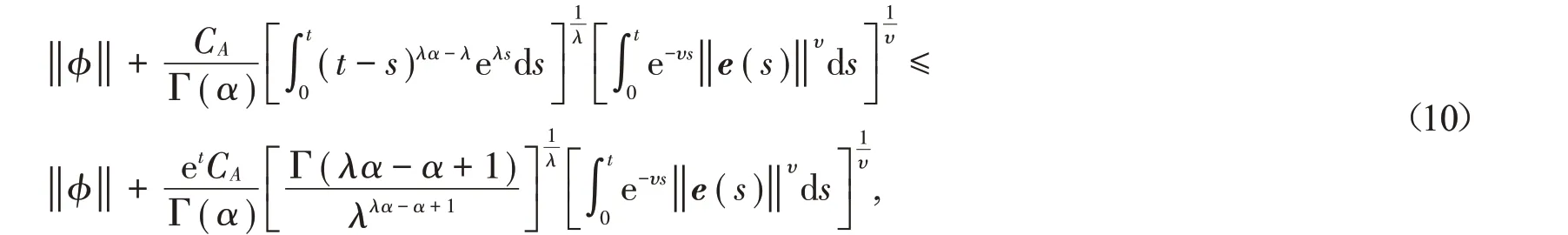
两边同时乘以e-t，得

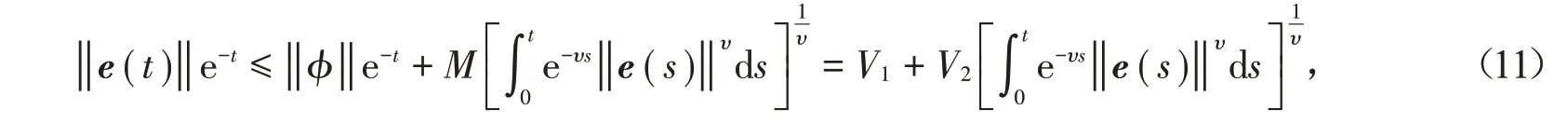
其中V1=e-t‖φ ，V2‖=M。

根据引理4和（10）式可得

因此，结合（11）～（13）式有

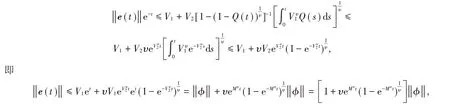
所以，根据定义3可知，如果‖ φ ‖＜δ，则‖ e(t) ‖＜ε，即分数阶神经网络的驱动系统（2）和响应系统（3）将实现准一致同步。

接下来，讨论分数阶滑模表面（5）式，K是矩阵不等式（7）的一个解，而分数阶滑模同步控制器为

时，驱动系统（2）和响应系统（3）的准一致同步问题，其中K1＞0为增益矩阵，‖ F^ (t) ‖是未知常数‖ F(t)‖的估算值，并且由分数阶自适应率确定：dαl^(t)=ω1‖ HB ‖‖ e(t)‖|σi(t) |-ω1ω2l^(t)，其中σ1，σ2为正设计参数。结合（4）式和（20）式，所得同步误差系统为

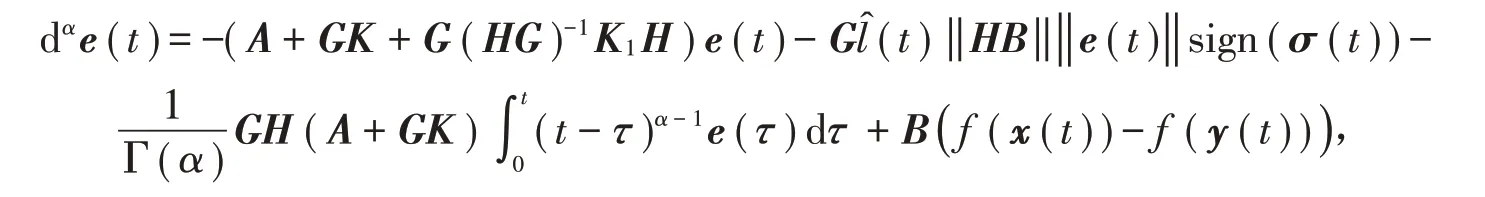
根据（8）式和（9）式，同理可得

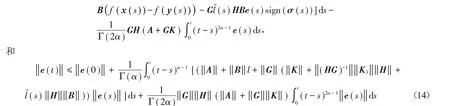
定理2 在假设（H1）和引理5的基础上，若0 ＜α ＜1，且1+

上式两边同时乘以e-t，得

根据引理4，结合（12）式、（13）式和（15）式，可得

即

‖ e(t) ‖≤Z1et+υZ1eteZ2υt(1-e-Z2υt)= ‖ φ ‖+υ‖ φ ‖e(SA+SB)υt(1-e-(SA+SB)υt)=[1+υe(SA+SB)υt(1-e-(SA+SB)υt)]‖ φ ‖，故而，由定义3可知，若‖ φ ‖＜δ，则‖ e(t) ‖＜ε，即分数阶神经网络的驱动系统（2）和响应系统（3）将实现准一致同步。

3 应用举例

为了验证所得定理的正确性以及可行性，现给出数值模拟。

例 讨论以下作为驱动系统的3维分数阶神经网络dαxi(t)=-aixi(t)+bijfj(xj(t)) +Ii，i=1,2,3，则矩阵形式为

图1、图2分别表示系统（16）和（17）、（16）和（18）之间的同步误差系统的状态轨迹，图3、图4分别表示系统（16）和（17）、（16）和（18）的同步误差的模。

图1 系统（16）和系统（17）同步误差状态轨迹

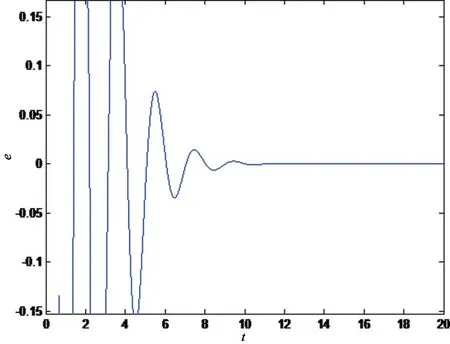
图2 系统（16）和（18）同步误差状态轨迹

图3 系统（16）和（17）的同步误差的模

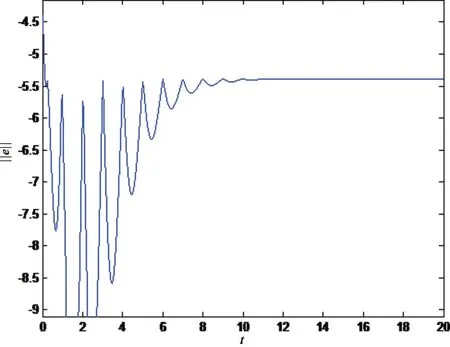
图4 系统（16）和（18）的同步误差的模

4 总 结

本文利用滑模控制策略、Volterra-integral等式和不等式技巧等,推导出分数阶神经网路系统的准一致同步性的充分性判据,并推广了先前工作，同时给出了仿真实例,以说明所探讨课题的可行性。接下来将进一步探讨基于滑模控制下的分数阶时滞神经网络的准一直同步问题、有限时间投影同步问题及全局Mittag-Leffler同步问题等。