Neuman平均关于算术和调和平均的精确不等式

王君丽，徐会作，李少云

（1.台州科技职业学院成人教育学院，浙江台州318020；2.温州广播电视大学教师教学发展中心，浙江温州325013；3.温州广播电视大学终身教育指导中心，浙江温州325013）

对 于p ∈ℝ 和a,b ＞0 且a ≠b，则p 阶 幂 平 均[1]=。对于固定a,b ＞0和a ≠b关于p ∈ℝ 是连续且严格单调上升的。调和平均、几何平均、算术平均和二次平均是幂平均的特殊情形：

分别是第一类Seiffert平均、Neuman-Sándor平均、第二类Seiffert平均、对数平均、第一类Yang平均和第二类Yang 平均[4]，并且有不等式L( a,b )＜V( a,b )＜P( a,b )＜U( a,b )＜NS( a,b )＜T( a,b )对所有a,b ＞0且a ≠b成立。

近年来，Schwab-Borchardt平均及其派生平均与不同阶幂平均的凸组合或各种特殊组合的序关系研究，得到国内外数学研究者的关注，有关Schwab-Borchardt平均的新派生平均被提出，一些重要平均值不等式被发现，Neuman平均就是其中一种。

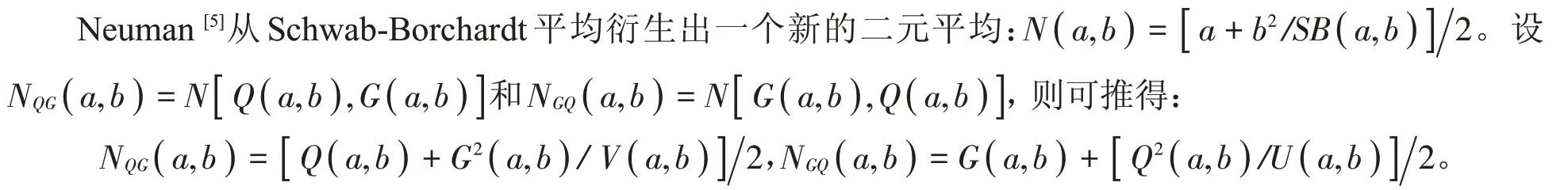
沈林昌等[6]证明了双向不等式

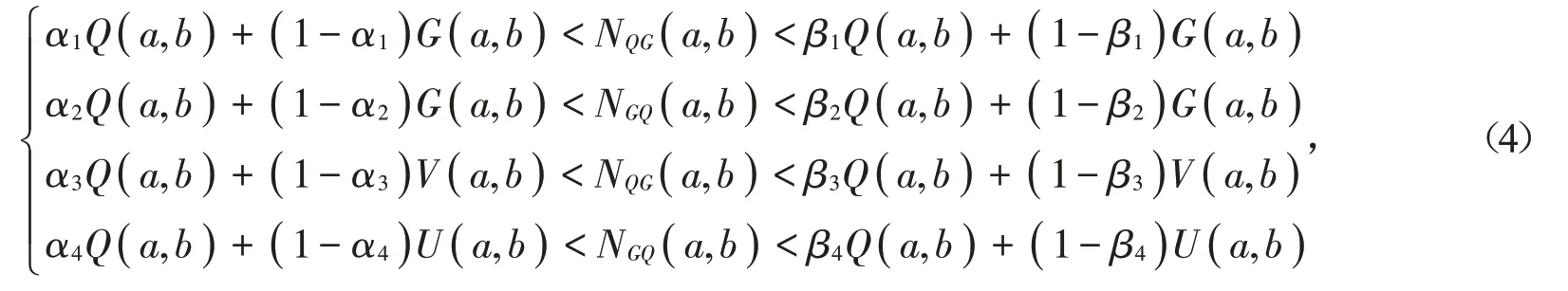
对所有a,b ＞0 且a ≠b 成立当且仅当α1≤1∕3，β1≥1∕2，α2≤2∕3，β2≥π∕4，α3≤0，β3≥1∕2，α4≤0 和β4≥( π2-8 )∕[ 4( π-2 )]=0.409 4…。

根据不等式（4），可推得

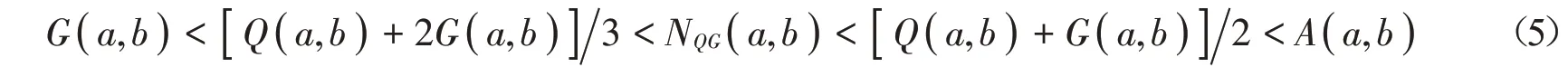
对所有a,b ＞0且a ≠b成立。

何 晓 红 等[7]证 明 了α ≤2log2=1.178 5… 和β ≥4∕3 是 双 向 不 等 式Mα(a,b)＜NGQ(a,b)＜Mβ(a,b)对所有a,b ＞0且a ≠b成立的最佳参数。受不等式(5)的启发，本文主要讨论是否存在最佳参数α1,α2,β1,β2∈( 0,1 )使得双向不等式

对所有a,b ＞0且a ≠b成立。

为了讨论上述问题，需要先介绍下面两个引理。

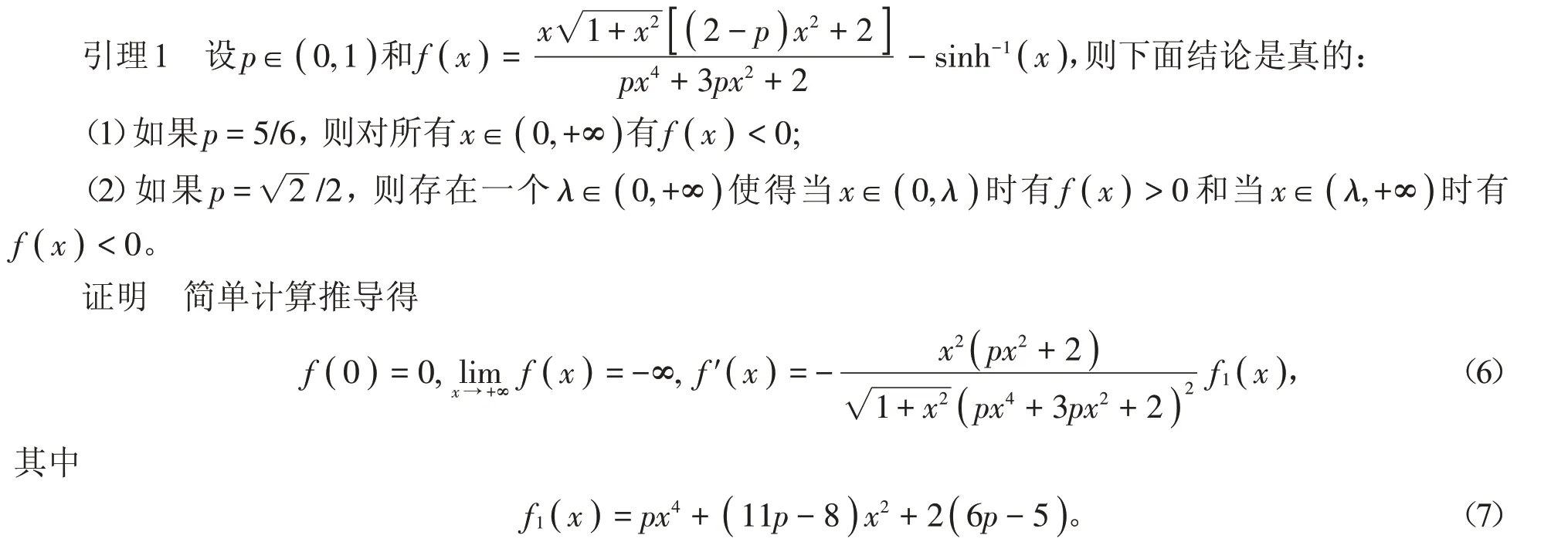
下面分两种情形讨论：

（1）当p=5∕6时，（7）式变为

对所有x ∈( 0,+∞ )成立，所以，由（6）、（8）式得到对所有x ∈( 0,+∞ )有f( x )＜0。

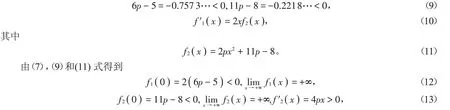
对所有x ∈(0,+∞)。

由（13）式可知存在λ0∈( 0,+∞ )使得当x ∈( 0,λ0)时f2( x )＜0，当x ∈( λ0,+∞ )时f2( x )＞0。由（10）、（12）式可知，当x ∈( 0,λ0)时f1( x )＜0；当x ∈( λ0,+∞ )时，f1( x )在区间( λ0,+∞ )内严格单调上升且f1( λ0)＜0，易知存在λ1＞λ0使得当x ∈( λ0,λ1)时f1( x )＜0，当x ∈( λ1,+∞ )时f1( x )＞0。综上可知，存在当x ∈( 0,λ1)时f1( x )＜0；当x ∈( λ1,+∞ )时f1( x )＞0。

同上分析，由（6）式并结合x ∈( 0,λ1)时f1( x )＜0，x ∈( λ1,+∞ )时f1( x )＞0，易知存在λ ＞λ1使得当x ∈( 0,λ )时f( x )＞0；当x ∈( λ,+∞ )时f( x )＜0。

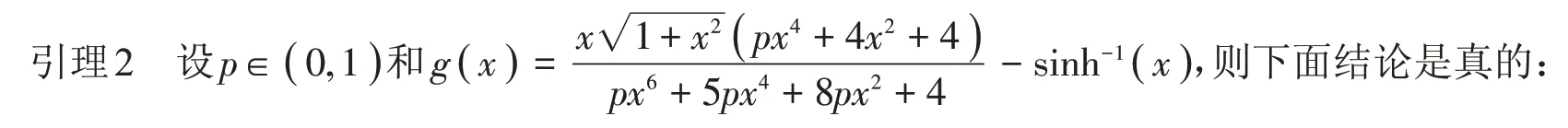
（1）如果p=5∕6，则对所有x ∈( 0,+∞ )有g( x )＜0；

（2）如果p=1∕2，则存在一个μ ∈( 0,+∞ )使得当x ∈( 0,μ )时有g( x )＞0 和当x ∈( μ,+∞ )时有g( x )＜0。

证明 简单计算可得

下面分两种情形讨论：

（1）当p=5∕6时，等式（15）化简为

对所有x ∈( 0,+∞ )成立。所以，由（14）、（16）式得到对所有x ∈( 0,+∞ )有g( x )＜0。

（2）当p=1∕2时，由（15）式可推得

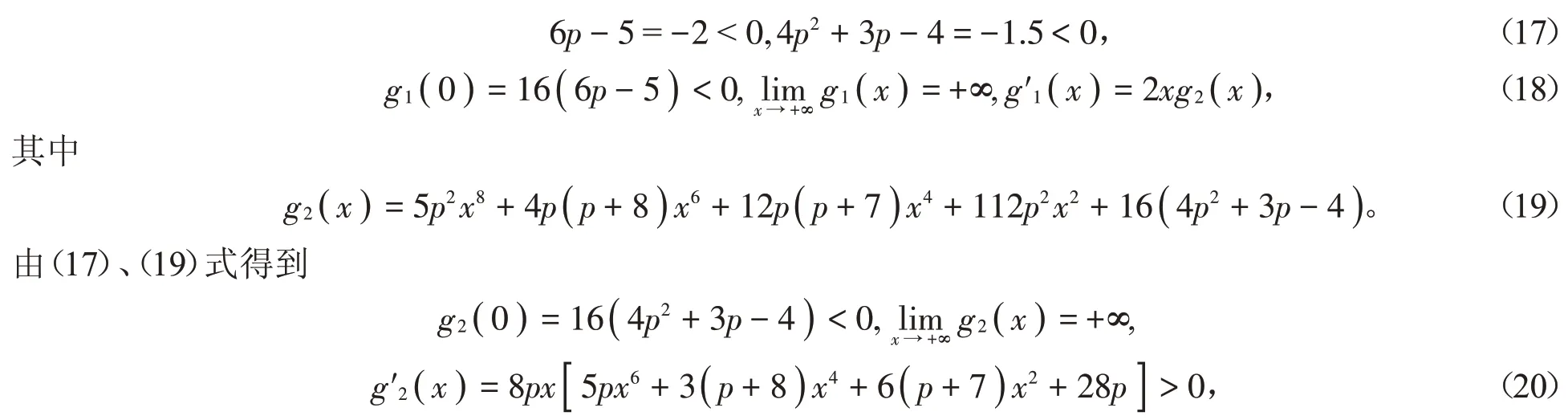
由（20）式可知存在μ0∈( 0,+∞ )使得当x ∈( 0,μ0)时g2( x )＜0，当x ∈( μ0,+∞ )时g2( x )＞0。由（18）式可知，当x ∈( 0,μ0)时g1( x )＜0；当x ∈( μ0,+∞ )时，g1( x )在区间( μ0,+∞ )内严格单调上升且g1( μ0)＜0，易知存在μ1＞μ0使得当x ∈( μ0,μ1)时g1( x )＜0，当x ∈( μ1,+∞ )时g1( x )＞0。综上可知，当x ∈( 0,μ1)时g1( x )＜0；当x ∈( μ1,+∞ )时g1( x )＞0。

同上分析，由（18）和（19）式，结合x ∈( 0,μ1)时g1( x )＜0，x ∈( μ1,+∞ )时g1( x )＞0，易知存在μ ＞μ1使得当x ∈( 0,μ )时g( x )＞0；当x ∈( μ,+∞ )时g( x )＜0。

下面给出本文的主要结论及证明。

定理1 双向不等式α1A(a,b)+ ( 1-α1)H(a,b)＜NQG(a,b)＜β1A(a,b)+ ( 1-β1)H(a,b)对所有a,b ＞0且a ≠b成立当且仅当α1≤∕2=0.707 1…，β1≥5∕6。

证明 根据调和平均H(a,b)，算术平均A(a,b)和Neuman平均NQG( a,b )是对称且一阶齐次的，不失一般性，假设a ＞b ＞0，设p ∈( 0,1 )和x= ( a-b )∕∈( 0,+∞)，则由（1）～（4）式得到

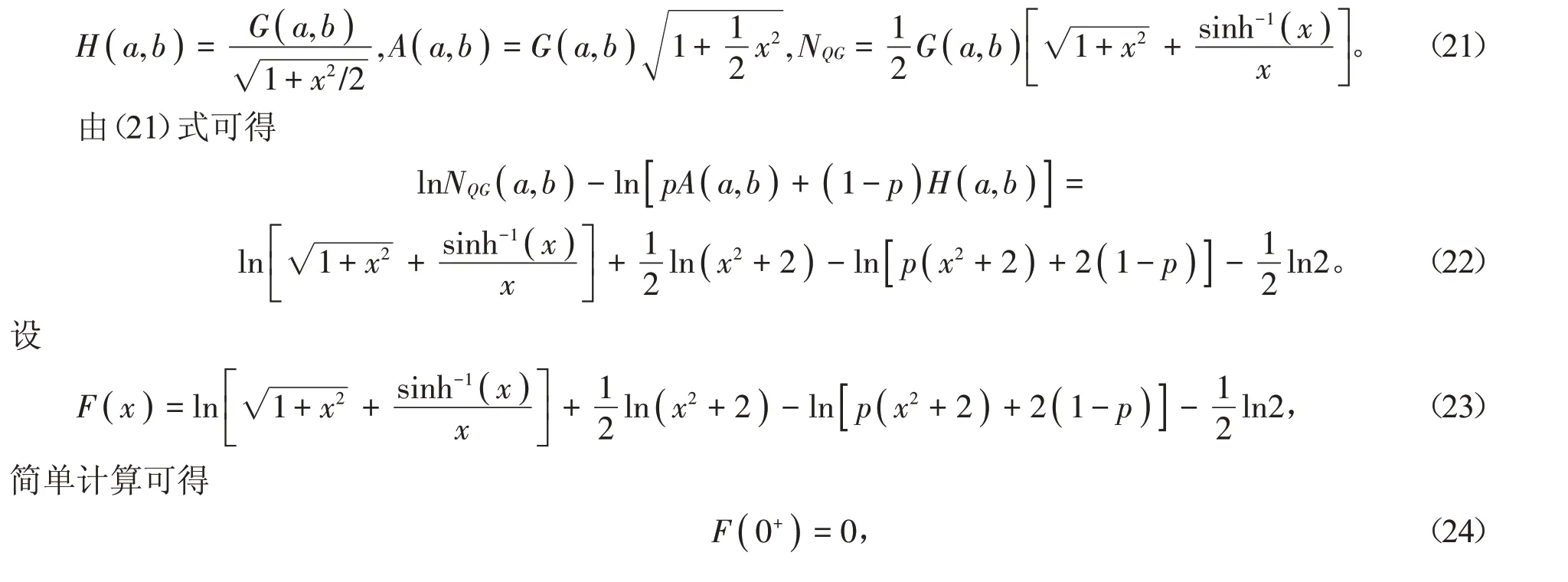
其中f(x)同引理1中定义。

下面分4种情形证明。

（1）如果p=5∕6，由（22）～（24）式和引理1（1）可知NQG( a,b )＜A( a,b )+H( a,b )对所有a,b ＞0且ab成立。

（3）如果p ＜5∕6，x ＞0和x →0，则应用幂级数展开得到

进一步由（22）、（23）式知，存在一个充分小实数δ0=δ0( p )＞0使得对所有( a-b )∕∈( 0,δ0)恒有

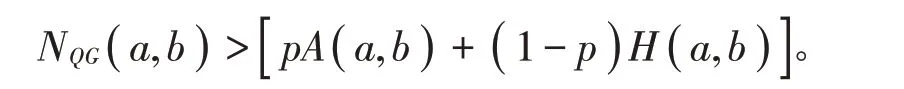
证明 不失一般性，假设a ＞b ＞0。设p ∈( 0,1 )和x= ( a-b )∕∈( 0,+∞)，则由(21)式得到

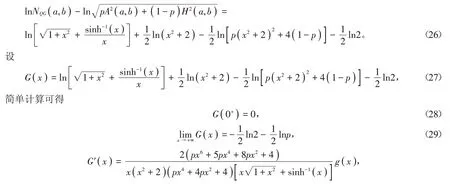
（1）如果p=1∕2，由（28）式和引理2（2）知存在一个μ ∈( 0,+∞ )使得函数G( x )在x ∈( 0,μ )内严格单调上升及在x ∈( μ,+∞ )内严格单调下降。注意到G( x )=0，所以由（26）～（28）式和协同函数G( x)的分段单调性可知对所有a,b ＞0且a ≠b成立。

（2）如果p=5∕6，由（26）～（28）式和引理2（1）可知a,b ＞0且a ≠b成立。