数字电子技术课程中卡诺图课堂教学方法探讨

卞维新，徐德琴

（安徽师范大学计算机与信息学院，安徽芜湖241002）

在数字电路教学过程中，逻辑函数的化简是重要的教学环节[1-3]。逻辑函数化简的结果将直接影响后续电路分析和设计的准确性和可靠性。逻辑函数的化简通常有两种方法：公式法和卡诺图法。公式法化简逻辑函数除了要求学生必须熟练掌握逻辑代数的运算法则和基本公式以外，还要求学生具备一定的化简技巧，而且化简结果是否最简判断困难，难度较高。在数字电路中，逻辑函数通常表示为逻辑变量最小项之和的形式。卡诺图（Karnaugh Map）[4]是由美国贝尔实验室的莫里斯·卡诺在1953年提出的，将逻辑函数中对应的最小项填入卡诺图中即可表示出对应的逻辑函数。卡诺图法形象直观，容易被学生掌握，且化简结果是否最简较易判断，缺点是化简变量个数不宜超过6个，否则化简将变得非常复杂，而在实际应用和教学中大多数逻辑函数的变量较少，卡诺图法基本可以满足要求。

1 卡诺图的构成

将逻辑函数中的逻辑变量分为两组，每一组逻辑变量按格雷码编码规则排列构成卡诺图，图中的每一个方格表示一个逻辑变量的最小项。格雷码本质上是一种二进制编码，在一组格雷码中，任意两个相邻的代码只有一位二进制数不同，具有反射和循环特性。由格雷码构成的卡诺图中的两个相邻最小项仅有一位变量取值不同（相反），因此可以很方便地消去不同的那个逻辑变量，从而达到化简的目的，这正是逻辑函数卡诺图化简的基本原理。

为了准确画出卡诺图，掌握自然二进制码到格雷码之间的相互转换是非常重要的。这不仅能够帮助学生掌握格雷码的特性，而且有助于学生更深入地理解卡诺图化简逻辑函数的原理。令Bn-1…B2B1B0为n位自然二进制数，Gn-1…G2G1G0为其对应的格雷码。

自然二进制码转换为格雷码：保留自然二进制码的最高位Bn-1作为格雷码的最高位Gn-1，次高位格雷码Gn-2为自然二进制码的最高位Bn-1与次高位Bn-2的异或，依次类推，由下面的递推式可得对应的格雷码：

格雷码转换为自然二进制码：保留格雷码的最高位Gn-1作为自然二进制码的最高位Bn-1，次高位自然二进制码Bn-2为自然二进制码的最高位Bn-1与次高位格雷码Gn-2的异或，依次类推，由下面的递推式可得对应的格雷码：

图1，图2给出了一个三位自然二进制码与格雷码之间相互转换的示意图，可以帮助学生更直观地理解二者的转换过程。

图1 三位自然二进制码转换为对应的格雷码示意图

图2 三位格雷码转换为对应的自然二进制码示意图

2 卡诺图的构建

为了化简逻辑函数，首先必须掌握如何将逻辑函数中的最小项填入卡诺图中准确的位置，即准确构建卡诺图。卡诺图的构建过程就是将n变量逻辑函数对应的全部最小项填入卡诺图中对应方格的过程。为了遵循构建过程的严谨性和科学性，在构建卡诺图时一般都是将逻辑函数中的最小项用逻辑值“1”填入，没有出现的最小项对应的方格填入逻辑值“0”或保持为空[5]。例如下面的逻辑函数，

对应的卡诺图如图3（a）所示。由于图3（a）所示卡诺图中填入的最小项都是用“1”表示，因此在课堂讨论中我们无法清晰区分填入的最小项，从而导致师生不能快速看出逻辑函数最小项和卡诺图中填入项的对应关系[6]，进而无法就一些疑问进行顺畅的讨论。在实际课堂教学过程中，尤其是刚刚开始卡诺图构建的教学时，学生往往会对某些填入项有疑问，因而需要老师在课堂教学中进行答疑。如果在课堂教学过程中学生对某个填入项有疑问，这样构建的卡诺图将导致学生很难把问题表达清楚，教师也很难快速、清晰地判断学生的问题。为了便于讨论卡诺图的构建过程，在课堂教学实践中，可为逻辑函数最小项设置一个唯一的身份标识（Identifier，ID），将其填入对应的卡诺图方格中，这样不仅使二者之间的一一对应关系清晰可见，而且也有助于初学者加深对逻辑函数最小项填入卡诺图过程的理解。这里为逻辑函数最小项绑定一小写字母的ID，改写（3）式的逻辑函数表达式如下：

对应的卡诺图如图3(b)所示。显然，此时再讨论某个填入项将会非常便利，也不会存在交流障碍。

图3 卡诺图构建实例

3 逻辑函数化简

卡诺图化简逻辑函数的过程就是画卡诺圈的过程。如何正确画出逻辑函数的卡诺圈是卡诺图化简逻辑函数的核心问题[7-8]。

3.1 几个定义

定义1 在逻辑函数F中，如果包含有“与”项，则每个“与”项都被称为F的蕴含项。

显然，由标准与或式构成的逻辑函数F中，每一个最小项自然是F的蕴含项，反映在F的卡诺图中，任何一个“1”项都是F的蕴含项。特别地，任意一个卡诺圈也是蕴含项。

定义2 若p 和q 分别为一逻辑函数F 的两个“与”项，如果p 中出现的所有逻辑变量在q 中一定出现，则称p为q的子项。

例如，令p=AB，q=ABC，由于出现在p中的逻辑变量A、B都出现在q中，因此p为q的子项。

定义3 令p是逻辑函数F的一个蕴含项，如果F中不存在除p外的蕴含项q是p的子项，则称p为F的质蕴含项，简称为质项。

按照最小项合并规律，在函数卡诺图中，如果某个卡诺圈不可能被其他更大的卡诺圈包含，那么，该卡诺圈所对应的蕴含项为质蕴含项。图4 给出了一个例子，在F 的卡诺图中，卡诺圈p1=BCˉ和卡诺圈p2=BCˉDˉ都是F的蕴含项，但是由于p1是p2的子项，因此p2不是F的质蕴含项。对于简单的逻辑函数，函数的最简式就等于所有质蕴含项之和，图5给出了一个实例，即G =p1+p2。但对于复杂的逻辑函数，找到所有的质蕴含项未必能得到函数最简式。图6给出了一个实例，其中p1,p2,…,p5是逻辑函数F的所有质蕴含项，但显然F ≠p1+p2+p3+p4+p5。因此为了准确表述函数的最简式，则有定义4。

图4 质蕴含项示例

图5 质蕴含项等价于函数最简式实例

图6 质蕴含项不等价于函数最简式实例

定义4 若逻辑函数的一个质蕴含项包含有不被函数的其他任何质蕴含项所包含的最小项，则此质蕴含项被称为必要质蕴含项，简称为必要质项。

定义4反映在函数卡诺图中可描述为：若某个卡诺圈包含了不可能被任何其他卡诺圈包含的1个方格，那么，该卡诺圈所对应的“与”项为必要质蕴含项。显然，逻辑函数的最简式等价于所有必要质蕴含项之和。

3.2 逻辑函数化简

基于卡诺图中最小项逻辑相邻的事实可知，相邻的两个最小项可以合并为一项，同时消去一个逻辑变量；相邻的4个最小项可以合并为一项，同时消去两个逻辑变量；同理，相邻的2n个最小项可以合并为一项，可以消去n个逻辑变量。这也是卡诺图化简法画卡诺圈的原则。卡诺图化简逻辑函数的过程就是画卡诺圈及求解必要质蕴含项的过程。为了便于课堂教学和讨论，首先采用第2节提出的构建卡诺图方法构建卡诺图；然后画卡诺圈，找出所有质蕴含项；最后检查所有质蕴含项，找出所有必要质蕴含项，写出逻辑函数最简式。下面以一个逻辑函数化简的例子讲述本文提出的方法。

例1 用卡诺图化简（3）式对应的4变量逻辑函数。

解 （1）为每一个最小项设置唯一标识ID，改写逻辑函数形式如上面（4）式所示；

（2）构建逻辑函数卡诺图，对应最小项用ID填入，如上图3（b）所示；

（3）画出卡诺图中所有质蕴含项对应的卡诺圈，得到逻辑函数的所有质蕴含项。

带有身份标识ID的卡诺图非常有利于课堂教学和讨论。例如，在讲授卡诺圈时，如果学生对某个卡诺圈有疑问，他能够快速、清晰地描述自己的问题：“b”和“d”为何能构成卡诺圈？“g”和“f”构成的卡诺圈为何不是质蕴含项？诸如此类的问题都能够顺畅地和老师在课堂上沟通，其他同学也能很快融入他的问题。显然，如果用传统的卡诺图（图6），老师讲授或学生提问都会有障碍，不利于课堂教学和讨论。

图7画出了卡诺图中所有质蕴含项对应的卡诺圈。依据对应的卡诺圈，可得逻辑函数对应质蕴含项分别为p1=，p2=A，p3=D，p4=，p5=ABD。

（4）检查所有质蕴含项，剔除冗余质蕴含项，找出所有必要质蕴含项，写出逻辑函数最简式。

对于复杂逻辑函数，检查质蕴含项是否是必要质蕴含项是比较困难的，一不小心就会出错。本文借鉴卡诺图构建过程中为最小项设置唯一ID的做法，通过为质蕴含项设置唯一ID（这里用一大写字母表示）来简化这一过程，使得这一过程更加直观、简单，也能够使学生更加容易理解和掌握。

在图7所示的卡诺图中，令卡诺圈p1-p5对应的ID分别为V、W、X、Y和Z，将各ID分别填入对应卡诺圈，改画卡诺图如图8所示。此时只要检查每一个大写字母是否会单独出现即可：如果某一个大写字母没有单独出现，则其对应的卡诺圈必为冗余质蕴含项，可以剔除；如果有单独出现，则其必为必要质蕴含项。由图8可以很容易看出，V没有单独出现，因此其对应的质蕴含项不是必要质蕴含项，为冗余质蕴含项，将其剔除，可得该逻辑函数对应的所有必要质蕴含项为：p2=A，p3=D，p4=ˉ，p5=ABD。进而可得逻辑函数F的最简式为：F=A+D++ABD。

图7 带有身份标识的逻辑函数卡诺图

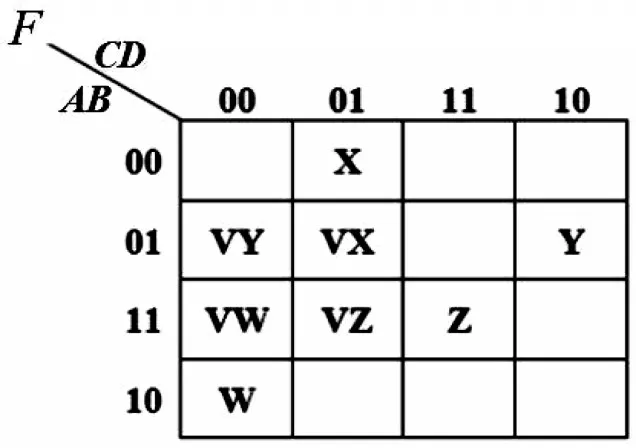
图8 带有身份标识的逻辑函数卡诺圈

当然，对于比较简单的逻辑函数卡诺圈可以直接看出结果，就不必非要使用该方法。对于比较复杂的逻辑函数，该方法不仅能够使得剔除冗余质蕴含项直观、简单，而且不容易出错。另外，在刚开始讲授这一部分内容时，此方法也能够帮助学生快速理解从质蕴含项到必要质蕴含项的原理，掌握卡诺图化简逻辑函数的技巧。

4 结束语

卡诺图化简逻辑函数的优点是简单、直观，有一套容易操作的化简步骤，且容易化简到最简并不易出错。这使得卡诺图化简在整个“数字电子技术”课程的教学中占据了重要地位，贯穿了整个课程的教学过程。如何在教学过程中使学生快速、准确地理解卡诺图化简的原理、方法和技巧是课程教学的重点和难点。本文基于教学实践经验，探讨了卡诺图化简逻辑函数的一些课堂教学方法，从卡诺图化简的原理出发，对化简方法和技巧的教学进行了有益的尝试，希望能够为学生提高卡诺图的学习效率提供一定的帮助。