量子力学教学中关于非守恒量期望值随时间演变的讨论

刘万芳，尹训昌，章礼华

（安庆师范大学物理与电气工程学院，安徽安庆246133）

如果量子力学是物理学中的“黄山”，那么，有许多的“景点”是引人入胜的。在这座“黄山”之中，物理量通常用算符来表示，算符理论则是重要的“景点”之一。在一个量子体系中，由于体系的状态一般是随时间变化的，这就导致算符的取值概率及期望值一般会随时间变化。但是，研究发现，在诸多物理量中，无论体系处于什么状态，有可能存在一个或者几个算符，它们的取值、取值对应的概率及期望值是不随时间变化的，这种特殊的算符称之为守恒量[1-4]。在守恒量理论的教学中，更多是注重守恒量的判断，学生如果掌握好守恒量的判断条件，这对于处理量子问题时的大局观提升有较好的帮助，可以利用守恒量的特点初步判断最终结果的可靠性。但是，勤于思考的同学在学习完本节内容后，自然会提出一个问题：当量子态发生变化的时候（不仅仅是量子态多了一个相位因子），量子力学中的非守恒量，它的取值、取值对应的概率及期望值就一定随时间变化吗？本人查阅了不少量子力学的教材，都没有找到这个问题相对完整的答案。这里通过两个例子来对这个问题做一些探讨。

在薛定谔绘景下，量子态是随时间变化的，通常记为ψ(t)。力学量有可能随时间变化，也有可能不随时间变化，隐去时间变量，通常简记为F^。那么，利用薛定谔方程及其共轭方程，可得到力学量期望值随时间的变化[1-4]：

如果一个不显含时间的力学量F^与H^ 对易，那么F^的平均值取值、取值对应的概率及期望值是不随时间变化的，即称F^ 是守恒量，与体系处于什么样的量子态无关。这里，通常将力学量不显含时间与H^对易视作是守恒量的判别条件。这实际上是个充分条件，因为对于含时不变量（也是守恒量），它却是显含时间的。

力学量F^ 在任意量子态上期望值不随时间变化才是守恒量的充要条件。对于初学者，由于视野不够、教师强调不够、研究经历缺乏等原因，容易忽略掉前提条件“任意量子态”，将其期望值不随时间的变化理解为守恒量的充要条件。为了澄清这一点，我们来讨论非守恒量的取值、相应的概率及其期望值随时间的变化。为了简化问题的讨论，这里不涉及力学量F^ 显含时间的情况，关于含时不变量的讨论，参见文献[2]。

例1 磁矩为μ=-αS 的电子在恒定外磁场B=Bex中运动（α 为大于零的实常数）。初始时刻电子处于Sz=ℏ∕2的态上。求t ≥0时的平均值。

解 首先给出体系的哈密顿量：H =-μ·B=-αSxB，通过计算可得到电子自旋状态：

例2 两自旋粒子构成的体系，初始时刻处于三重态之一的|1,-1＞态，两粒子之间存在非线性相互作用，通常称为一轴横场扭曲模型[5]。体系的哈密顿量H =+ΩSz，Ω刻画了横场的强度。取自然单位ℏ=1。试求：（1）两粒子t ＞0时刻的状态；（2）t ＞0时刻总自旋3个分量的取值、相应的概率及期望值。

解 通过计算，可得到在S^z表象下两粒子体系t ＞0时刻的状态为[6]

对于自旋的3个分量，不难得到其取值分别为ℏ、0、-ℏ，并且，不会随时间变化。对于S^x，与3个本征值对应的3个本征态分别为

在ψ(t)态上测量3个可取值，相应的概率为

在ψ(t)态上测量3个可取值，相应的概率为

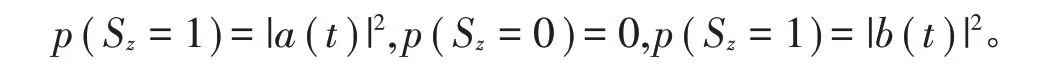
图1 （a）S^y 3个取值的概率和（b） 3个取值的概率随时间的演变

第2种情况，取Ω ≠0。此时，不同于第1种情况，自旋的3个分量都不是守恒量。对于自旋分量，3个取值±ℏ和0，相应的概率分别都随时间作周期性变化，但是，取值为±ℏ总是相等，从而保证其期望值还是为0，如图2（a）中3条曲线所示。对于自旋分量S^y，3个取值±ℏ和0，相应的概率分别也都随时间周期性变化，类似于。同样，取值为±ℏ总是相等，从而保证其期望值也还是为0。不同的是，概率p(Sy=0)和p(Sx=0)的单调性总是相反，p(Sy=±1)和p(Sx=±1)的单调性总是相反，分别如图2（a）中3 条曲线和图2（b）中的3条曲线所示。对于自旋分量，3个取值的概率与Ω =0时的曲线类似，不同的是，由于Ω的存在，不能处于三重态之一，如图2（c）中3条曲线所示。本质上是横场的存在，提高了量子态的自旋相干性[7]。

综上所述，在量子力学中，（1）无论是守恒量还是非守恒量，其取值一般不会随时间变化，即本征值谱是静态的，这个是由体系的结构决定的，除非这个量显含时间，例如，含时哈密顿量其本征值谱是动态的。（2）一个物理量虽然不是守恒量，它的某个或某几个取值对应的概率有可能不会随时间变化，该物理量的期望值随时间变化。（3）一个物理量虽然不是守恒量，它所有取值对应的概率有可能都随时间变化，但该物理量的期望值却不随时间变化。（4）一个物理量虽然不是守恒量，其所有取值对应的概率有可能不会随时间变化，导致物理量的期望值也不会随时间变化。值得说明的是，在一个或者某几个特殊的量子态上某个物理量的可取值、可取值对应的概率及期望值不随时间变化，从而将这个物理量视作守恒量是不对的。因为守恒量对量子态没有要求，即任意一个量子（束缚）态作为初始态[1-2]，其可取值、可取值对应的概率及期望值都不随时间变化，这恰恰是非守恒量不具备的条件。（5）定态是特殊的量子态，在该态上任意力学量（当然包括守恒量和非守恒量）的可取值、可取值对应的概率及期望值都不随时间变化[1,2,4]。

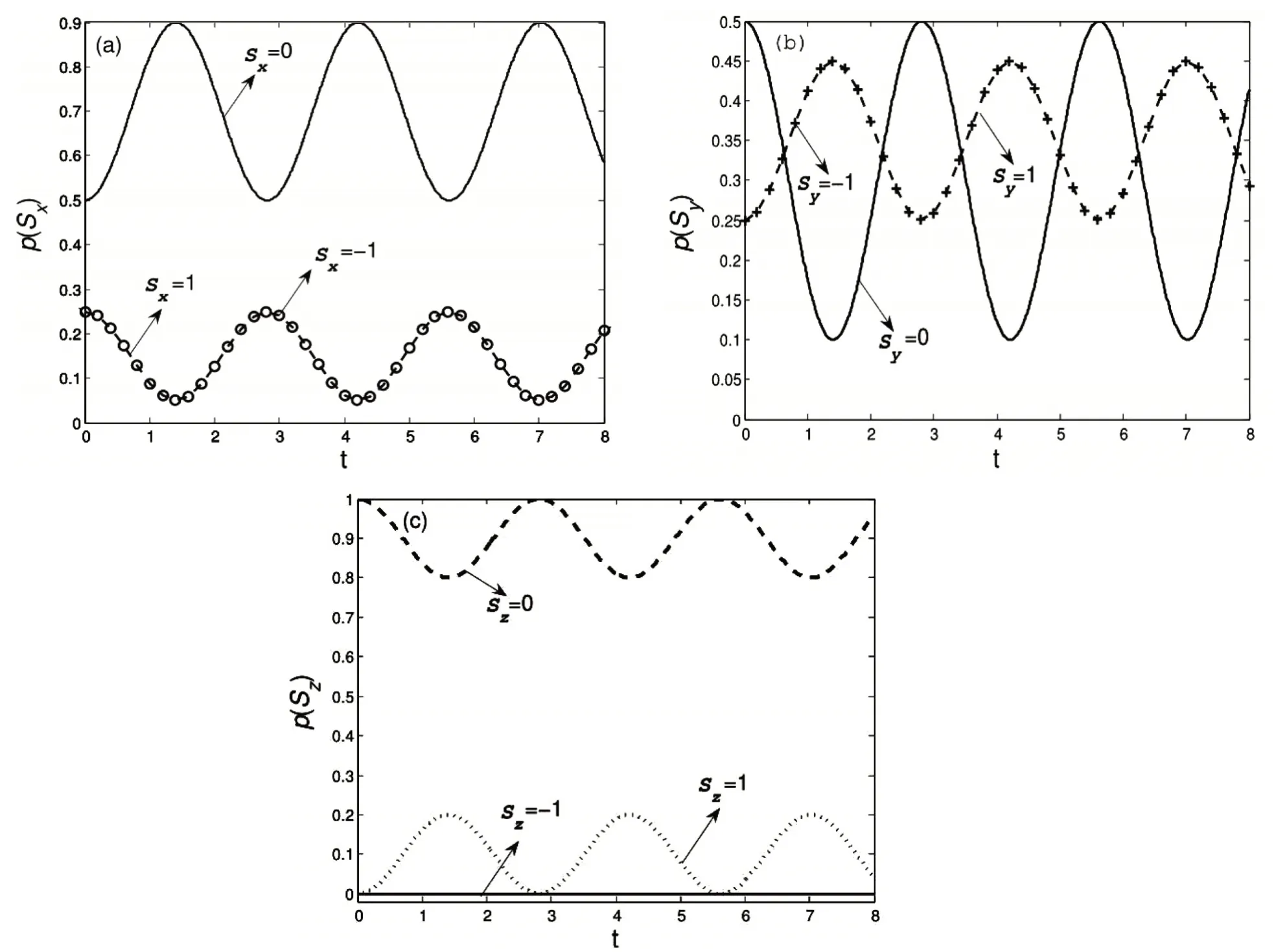
图2 （a）S^x算符3个取值的概率，（b）S^y算符3个取值的概率和（c）算符3个取值的概率随时间的演变

在教学的安排方面，非守恒量的期望值问题可以作为一个疑问预先留在力学量期望值随时间变化的教学的最后，等到自旋部分结束时，通过对上面两道例题的解答和讨论来给出答案。这样不仅解决了问题，巩固了前面所学的知识，还将“黄山”中的几个“景点”联系了起来，这无疑对培养学生量子力学大局观是有很大帮助的。