分数阶非线性变时滞脉冲微分系统的有限时间稳定性

吴 桐，张志信，蒋 威

（安徽大学数学科学学院，安徽合肥230601）

自分数阶微积分这一概念在300多年前被提出至今，分数阶微积分理论已日趋成熟与完善。分数阶微积分因具有很好的遗传性质较之经典微积分能够更精确地描述实际应用中的系统，这引起了很多学者对分数阶微分系统的广泛关注。近三十年以来，分数阶微分系统由于其在黏弹性系统、电介质极化、生物系统以及凝聚态物理等各个领域的广泛应用，得到了更为深入的研究[1-3]。有限时间稳定的概念早在1953年由苏联学者Kamenkov[4]提出：如果在一给定的时间区间上给初始条件一个界，它的状态变量不会超过某一个临界值，那么这个系统在给定的时间区间上是有限时间稳定的。到目前为止，经典微分方程以及分数阶微分方程关于有限时间稳定的研究较为广泛，近年来国内外学者对于分数阶有限时间稳定性问题已经展开研究并取得了丰富的理论成果[5-12]。Lazarevic[5]运用广义Gronwall不等式给出了一类具常时滞的分数阶线性微分系统的有限时间稳定的充分性条件，我国学者张秀云[6]也对此类线性时滞系统给出了相关的有限时间稳定性结果。文献[7-8]讨论了一类分数阶神经网络的有限时间稳定性。关于分数阶非线性系统的有限时间稳定性问题，Li等[10-11]通过引入滞后Mittag-Leffler型矩阵函数给出了一类分数阶非线性时滞微分方程的显式解，进而给出了方程有限时间稳定的充分性条件。近年来，脉冲微分系统的有限时间稳定问题也引起了国内外学者们的广泛关注[13-16]，相关学者研究并分别给出了线性时变微分系统、线性时变奇异微分系统、分数阶线性时变系统，以及分数阶时滞系统在带脉冲情况下的有限时间稳定性判据。然而，对同时含有脉冲和时变时滞因素的分数阶微分系统的有限时间稳定性问题研究结果不多。本文在现有研究成果的基础上，研究具有时变时滞的分数阶非线性脉冲微分系统的有限时间稳定性问题。

记号：ℝn表示n维欧氏空间；ℝn×m为所有n×m实矩阵的集合；自然数集记为ℕ；ℝ+=[ 0,+∞)，时间区间J=[ 0,T ]，其中T ∈ℝ+是有限数；ℂ表示全体复数集；Cn[ 0,+∞)为定义在[ 0,+∞)上的所有具有n阶连续导数的函数全体；记PC1( [ -τ,T ],ℝn)为[ -τ,T ]上具有左连续导数的所有n维分段连续函数全体构成的Banach空间；任意x ∈ℝn，‖ x ‖为通常的欧氏范数；任意为矩阵A的最大奇异值，其中AT为矩阵A的转置，λmax表示矩阵的最大特征值；对于函数矩阵A( t )，σA表示A( t )关于t的最大奇异值；n阶单位矩阵记为In。

1 准备知识

下面给出分数阶微积分的一些相关定义与引理。不失一般性，本论文中所有分数阶微分、积分的下限均设为0。

下面考虑如下分数阶非线性变时滞脉冲系统：

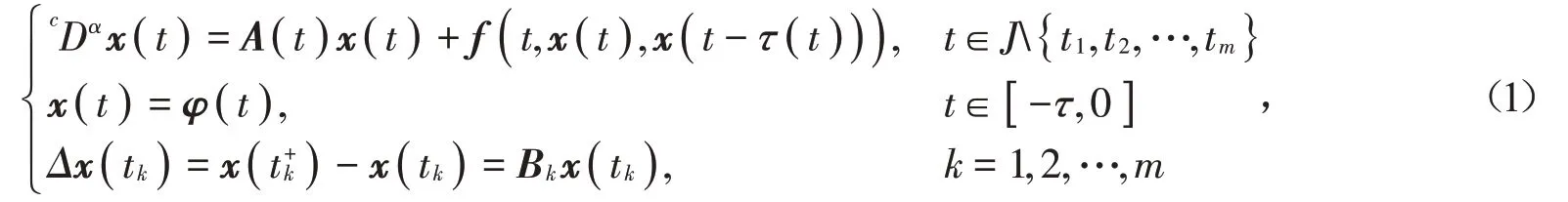
其中cDαx( t )为x( t )的α 阶Caputo 导数，0 ＜α ＜1；t ∈[ -τ,T ]，x ∈ℝn为状态变量，0=t0＜t1＜…＜tm＜tm+1=T；A( t )= ( aij( t ))n×n,aij( t )∈C[ 0,T ]；非线性泛函f( t,x( t ),x( t-τ( t )))∈C( [ 0,T ],ℝn)，且满足f( t,0,0 )≡0；τ( t )为J 上的连续函数，且0 ≤τ( t )≤τ；φ( t )∈C( [ -τ,0 ],ℝn)为给定的初值函数；Bk∈ℝn×n为常值矩阵，且Bk≠In。

为了研究系统(1)，现作如下假设：

定义4[12]给定正实数δ,ε，δ ＜ε，则满足初始条件x( t )=φ( t ),-τ ≤t ≤0 的系统(1)关于( δ,ε,φ,J)是有限时间稳定的当且仅当‖ φ ‖c≤δ ⇒‖ x( t )‖＜ε，∀t ∈J，其中‖ φ‖c=‖ φ( θ )‖。

引理2[18]假定(H1)、(H2)成立，则x ∈PC1( [ -τ,T ],ℝn)为初值问题(1)的解当且仅当x( t )满足以下分数阶积分方程

2 主要结果

证明 对于t ∈( tn,tn+1],0 ≤n ≤m，由引理2有

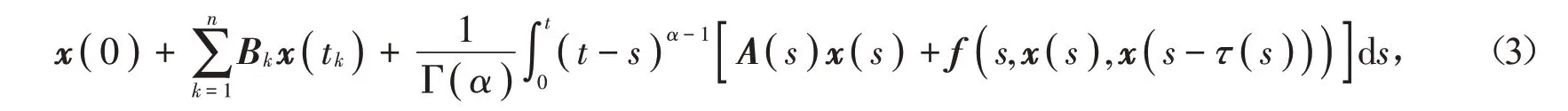
对（3）式两端取范数，则由范数的性质及(H2)有

综上，定理得证。

定理2 假定(H1)、(H2)成立，若系统（1）关于给定的δ,ε，δ ＜ε满足条件：

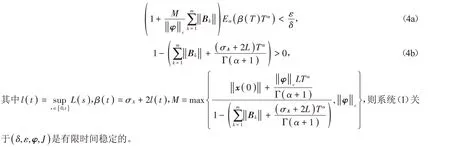
证明 由引理2可知，系统（1）具有如（2）式的解，则对于t ∈( tn,tn+1],0 ≤n ≤m，有

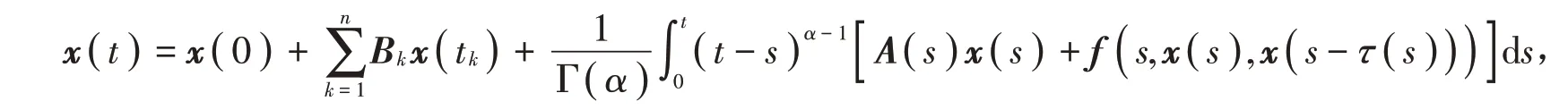
对上式两端取范数，由条件（4b）及（H2）有

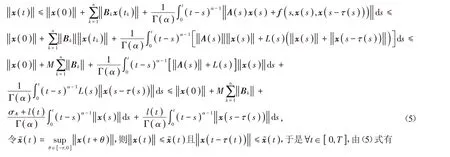
推 论 若 假 设 (H1) 中 L( t )≡L ( L 为 非 零 正 常 数），也 即 非 线 性 泛 函f( t,x( t ),x( t-τ( t )))∈C( [ 0,T ],ℝn)在[ 0,T ]是Lipschitz连续的，则将定理2中的条件（4a）改为

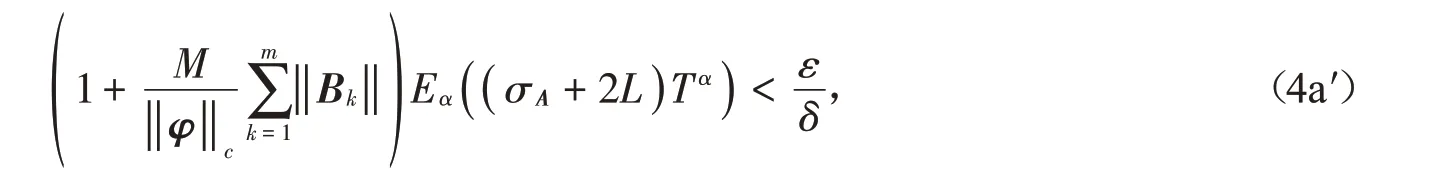
则系统（1）关于( )

δ,ε,φ,J 仍是有限时间稳定的。

3 数值算例

下面给出具体的数值算例来说明定理2的条件是有效的。例 考虑如下分数阶非线性脉冲时滞系统：

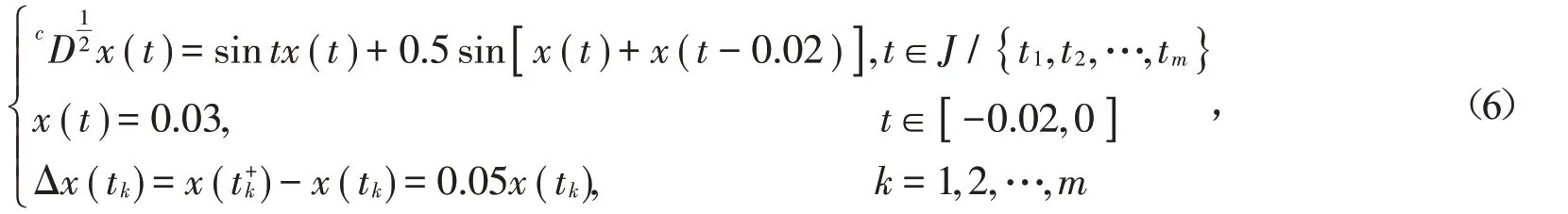
在该例中，A( t )=sin t，τ( t )=0.02，f( t,x( t ),x( t-τ( t )))=0.5 sin[ x( t )+x( t-0.02 )]，给出的有限区间J=[ 0,0.1 ](T =0.1)，考虑到x( t )的左连续性，这里给出9个脉冲点tk=0.01k(k=1,2,…,9)。容易看出‖ x( 0 )‖=‖ φ‖c=0.03，L=0.5，‖ Bk‖=0.05，σA=sin0.1。由定理1可以计算得到

取δ=0.03,ε=0.21，验证定理2的条件（4a）如下

4 结 论

本文针对一类分数阶非线性变时滞脉冲微分系统的有限时间稳定性问题进行了研究，所研究系统含有脉冲和时滞的因素，使得所研究的系统对具体模型有更好的适应性。主要利用系统解的结构和广义不等式得到了保证系统有限时间内稳定的充分条件，改进了现有的处理技巧，推广了相关的研究结果。同时，通过具体模型对定理的条件进行了验证，证明了定理条件的有效性和合理性。