基于认可度的主服务博弈频谱共享算法

于永生 李翠然 谢健骊

(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)

0 引 言

无线电频谱是一种稀缺资源，在移动通信中发挥着不可替代的重要作用。近年来，随着移动互联网和物联网的快速发展，各类新业务和应用场景不断涌现，催生了大量高速率、低延迟的传输需求，导致无线数据流量激增，频谱短缺加剧[1-2]。为了应对不断增长的流量负载，探索额外的可用频谱正变得越来越迫切。目前各国的频谱管理普遍采用静态分配策略，即频谱被划分成不同的授权频段，并固定分配给特定的用户独占使用，尽管这样避免了用户间的相互干扰，但同时也造成了频谱资源的严重浪费[3]。基于认知无线电的频谱共享能极大提高频谱使用的灵活性，进而促进频谱资源的高效利用，因此被认为是解决频谱短缺问题的有效方案[4]。在认知无线电频谱共享中，次用户(认知用户)可以租借使用主用户(频段授权用户)暂时空闲的频谱资源，并向主用户支付一定的费用。这种市场驱动的频谱共享模式被称为频谱交易，因其在分配效率、公平性和经济激励等方面的优势，已成为无线通信领域中的研究热点之一[5-13]。

Li等[6]提出了一种基于霍特林模型的频谱定价迭代算法，将频谱的质量差异和次用户的随机偏好作为必要因素纳入考虑，以提高频谱交易中次用户的效用。Khairullah等[7]提出了一种基于双重拍卖的频谱共享框架，其中信号与干扰加噪声比(SINR)不仅是信道的质量指标，同时也被作为次用户对频谱偏好的度量。据此设计的“赢家决定”和定价机制实现了频谱与次用户的双向匹配。Khaledi等[8]提出了一种整合多臂赌博机模型的频谱拍卖机制，并制定了指数型的频谱分配策略，允许次用户根据信道质量变化动态调整频谱估值，目标是最大化预期的社会福利折扣。Niyato等[9]利用寡头垄断市场和Bertrand博弈模型提出了一种基于纳什均衡的频谱定价算法，并分析了信道质量、频谱替代性等系统参数对均衡价格的影响，算法旨在最大化主用户在服务质量(QoS)约束下的利润。

次用户在频谱交易中作为买方，通常可以从多个主用户处购买频谱。频谱的垂直差异(即信道质量差异)对频谱交易的影响已在现有文献中得到充分考虑。本文考虑另外两个被忽略的重要影响因素：① 不同的主用户拥有各自不同的授权频段，这些频谱因频率的高低不同而具有水平差异，具体表现为不同的电磁波传播特性、抗干扰能力、覆盖能力和信息承载能力等，次用户倾向于选择更加适宜承载其业务的频谱，即次用户在频谱选择上具有频段偏好；② 有的主用户售让频谱时隙后，为了最大化自身收益，可能会出现提前收回频谱的不诚信行为(包含但不限于：访问频谱并形成干扰、将频谱同时租售给其他的次服务等)。针对这两个因素，本文设计了认可度机制，并将其引入到基于Bertrand博弈的频谱共享模型当中，进一步提出了基于认可度的主服务博弈频谱共享算法(静态/动态)和与之对应的频谱租赁框架，旨在促进达成更加合理、有效的频谱共享。

1 频谱共享场景及博弈模型

1.1 频谱共享场景

将主用户与次用户间的频谱共享问题扩展为主服务与次服务间的频谱共享问题。如图1所示为一个认知频谱共享场景。N个主服务工作在各自不同的授权频段上，均愿意租让部分频谱给次服务使用，以获取额外收入。各个主服务都是理性而自私的，彼此间通过竞争方式向次服务租让频谱，目标是通过频谱共享来最大化各自的利润。单个主服务中包含多个主用户，这些主用户均连接于一个主服务控制器(Primary Service Controller，PSC)。与之类似，次服务中的所有次用户连接于一个次服务控制器(Secondary Service Controller，SSC)。主/次服务的频谱可以在多个主/次用户之间共享，其中基站或接入点控制认知无线电网络中频谱机会的分配，从而充当服务控制器。

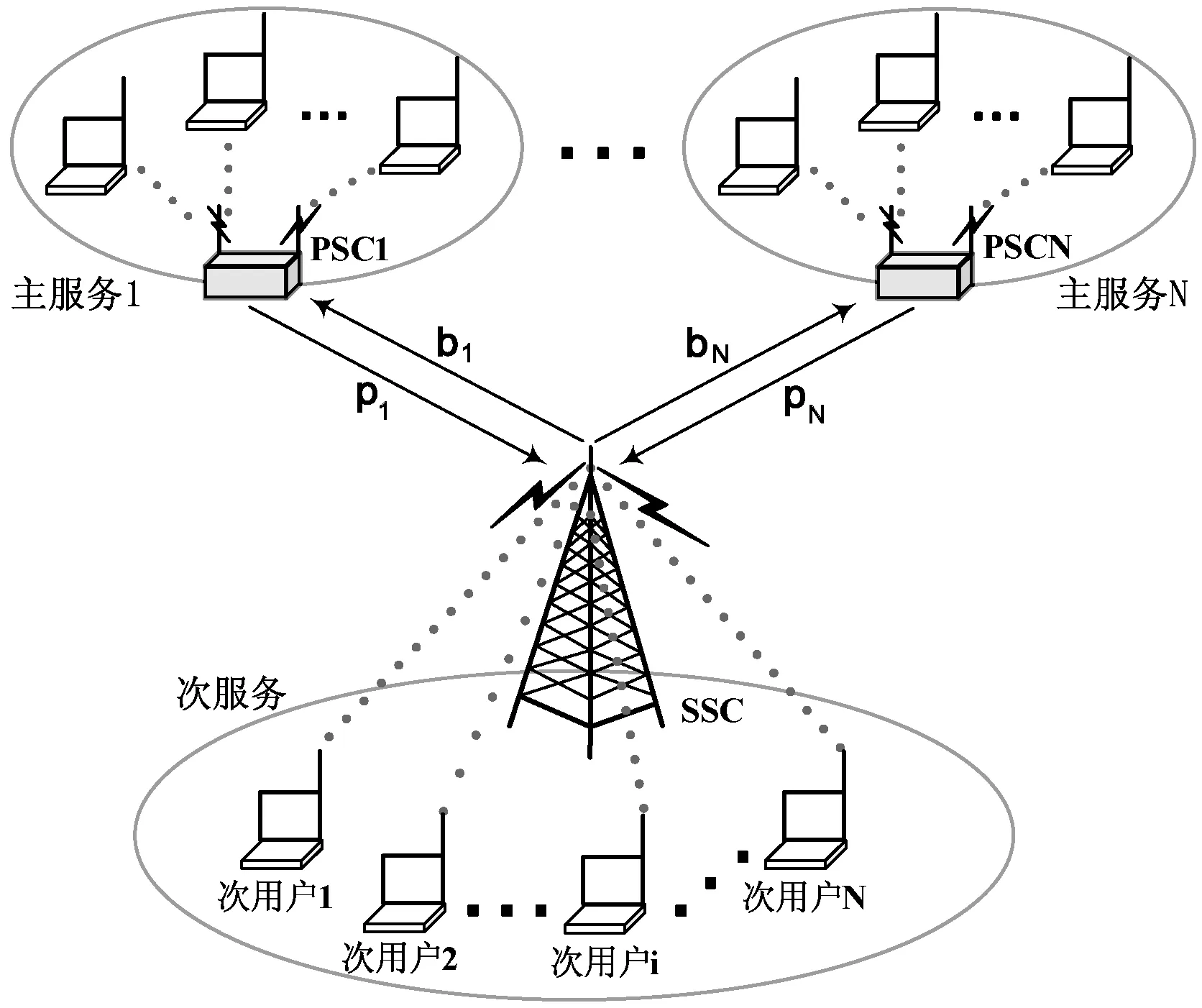
图1 频谱共享场景

次服务同时从N个主服务处租借频谱，若主服务i对单位带宽频谱的定价为pi，则次服务对其产生带宽为bi的频谱需求。次服务获得的频谱由SSC按照一定的规则和复用方式(FDM/TDM/CDM)向所有次用户分配，次用户利用自适应调制在所分配的频谱上进行传输。次用户获得的频谱既可以用于次用户与SSC之间的通信，也可以用于次用户的自组织网络(Ad Hoc网络)内的通信。由于主服务之间进行价格竞争，彼此的策略选择(频谱定价)相互影响、相互制约，单个主服务的最优化可能会与其他主服务的最优化产生冲突，因而需要引入博弈论来进行分析。

1.2 频谱共享博弈模型

频谱共享的博弈模型可以表示为:

G={N,{Si}i∈N,{Ui}i∈N}

(1)

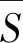
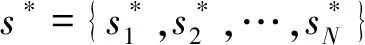
在本文中，各个主服务根据观察到的信息进行策略调整，直至任何一个主服务都无法通过单独改变策略而增加自身利润时，博弈达到纳什均衡。此时所有主服务策略的组合(即频谱价格组合)和次服务相应的频谱需求量即为最终的频谱共享方案。

2 静态博弈算法

2.1 传统的次服务效用函数

次服务的效用函数被用来量化次服务对不同主服务的频谱需求。次服务获得频谱后，利用自适应调制，可以基于信道质量动态调整传输速率，传统的次服务效用函数定义如下[9]：

(2)

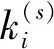
(3)

式中：γi表示次服务使用主服务i的频谱进行传输时接收器的信噪比；K是由误码率门限值决定的常数：

(4)

式中：BERtar表示次服务传输的目标误码率。

2.2 改进的次服务效用函数

引入认可度参数及其影响因子，定义次服务的效用函数如下：

(5)

式中：θ={θ1,θ2,…,θN}表示认可度的集合，元素θi∈[0,1]是次服务对主服务i的认可度，θi越大表示认可度越高，特别的，当θi=1时，表示次服务对主服务i完全认可，而当θi=0时，则表示完全不认可；u∈[0,+∞)是认可度参数的影响因子，用来表示认可度参数对博弈的影响程度，当u越大，表示认可度参数对博弈的影响程度越重，特别的，当u=0时，认可度参数不对博弈产生影响，效用函数退化为传统的效用函数。

2.3 主服务的利润函数

为了获得主服务的利润函数，需要考虑主服务在频谱共享中的收入和成本。主服务的收入包括从主用户收取的固定费用和从次服务收取的频谱租赁费用。成本来自将部分频谱租让所引起的性能退化，即主用户的QoS降级，并且主服务租让出的频谱越多，自身剩余的可用频谱就越少，主用户所遭受的QoS降级也越严重。定义利润为收入减去成本，则主服务i的利润函数可表示如下[9]：

(6)

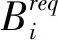
2.4 纳什均衡求解

静态博弈的纳什均衡可以利用最优反应函数求得，主服务i的最优反应函数定义如下：

(7)

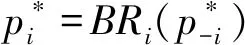
次服务根据效用最大化原则确定对各个主服务的频谱需求，由式(5)得：

(8)

令∂U(b,θ)/∂bi=0对∀i成立，解得次服务的需求函数如下：

Di(p)=Di(p-i∪{pi})=D1(p-i)-D2pi

(9)

式中：

将需求函数代入主服务的利润函数得：

Pi(p)=pi(D1(p-i)-D2pi)+c1Mi-

(10)

对pi求偏导，得到主服务的边际利润如下：

D1(p-i)-2D2pi

(11)

令∂Pi(p)/∂pi=0对∀i成立得：

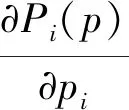
(12)

式中：i=1,2,…,N。

在完全信息条件下，式(12)中的所有参数可用，通过求解该方程组，即可获得博弈的纳什均衡p*。

2.5 纳什均衡存在性的数学证明

为了使提出的算法有意义，必须确保其存在纳什均衡。本节利用超模博弈条件，通过数学推导对纳什均衡的存在性进行证明。

首先给出两个相关定理：

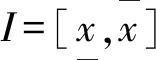
定理2[15]若策略型博弈G={N,{Si}i∈N,{Ui}i∈N}为一个超模博弈，则纯策略的纳什均衡存在，且对于策略空间上给定的序结构，最大最小的纯策略纳什均衡存在。

然后根据定理进行证明，过程如下：

继续对式(11)pj求偏导得：

(13)

又：

(14)

代入式(13)有：

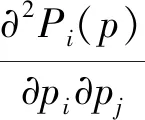
(15)

可见博弈符合超模条件，因此纳什均衡存在。

3 频谱租赁框架及认可度更新机制

构建的频谱租赁框架如图2所示。算法完整运行一次，称为一个算法周期，算法周期运行一次结束到达稳定状态(纳什均衡)形成一个频谱租赁的租期，租期结束再运行下一个算法周期，形成新的租期。每个算法周期分三个阶段完成：阶段1为认可度更新环节；阶段2为主服务博弈环节；阶段3为纳什均衡价格确定环节。在阶段1中，次服务根据收集到的信息(主服务的频段信息、诚信相关历史信息)更新对各个主服务的认可度，得到认可度集合，通过该阶段，次服务给出买家意愿。在阶段2中，主服务之间进行价格博弈(静态/动态博弈)，通过该阶段，主服务间进行竞争。在阶段3中，根据博弈结果得到各个主服务的纳什均衡价格，并将该价格向次服务反馈，通过该阶段，形成频谱租赁的租约，并进入相应的租期。

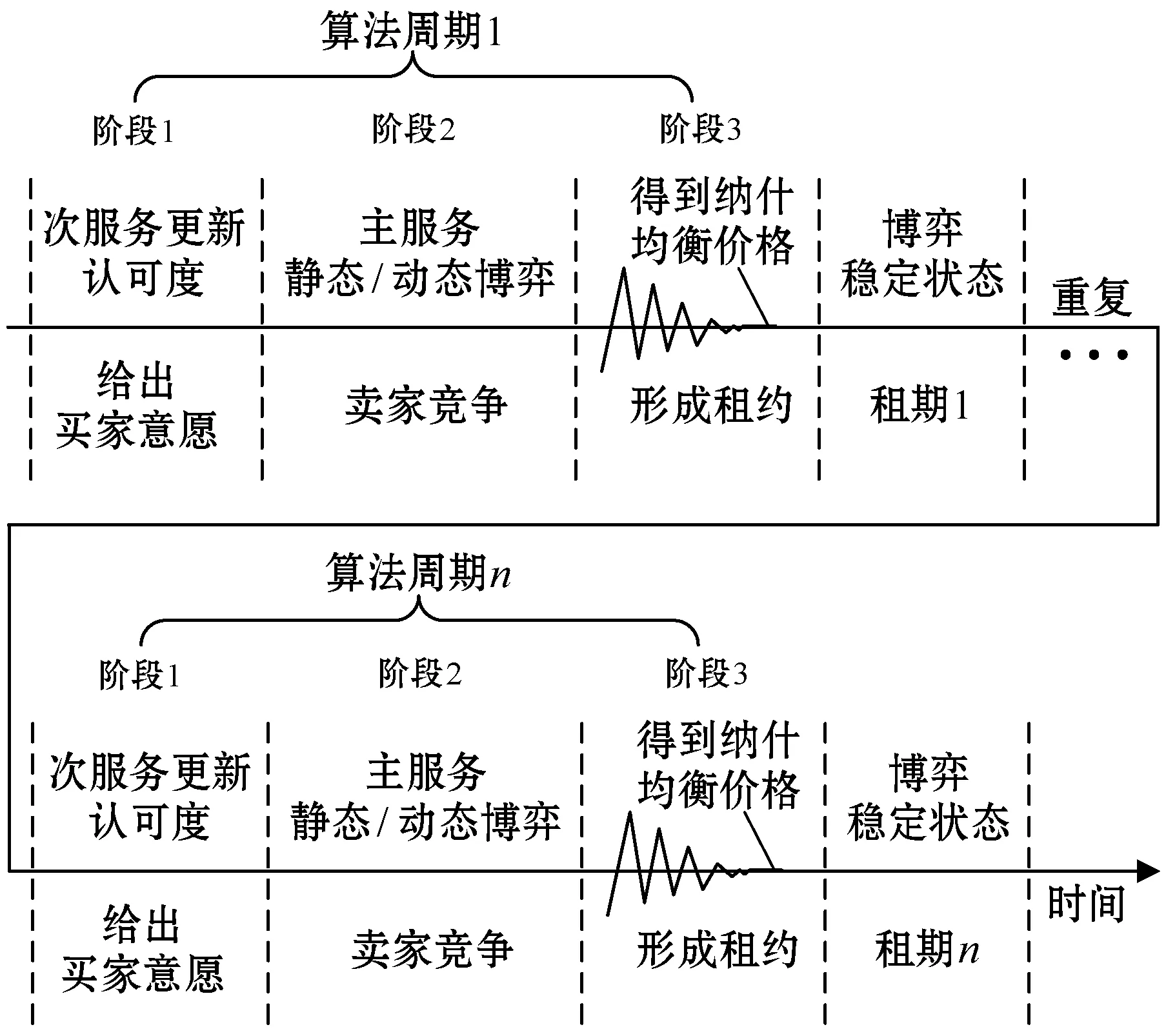
图2 频谱租赁框架

(16)

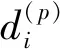
任意的主服务可以在某个租期结束后(下一个算法周期开始前)自由选择加入或退出频谱交易。在每个算法周期的阶段1，确定参加频谱交易的主服务后，次服务收集它们的信息，并更新对它们的认可度，更新过程如图3所示。

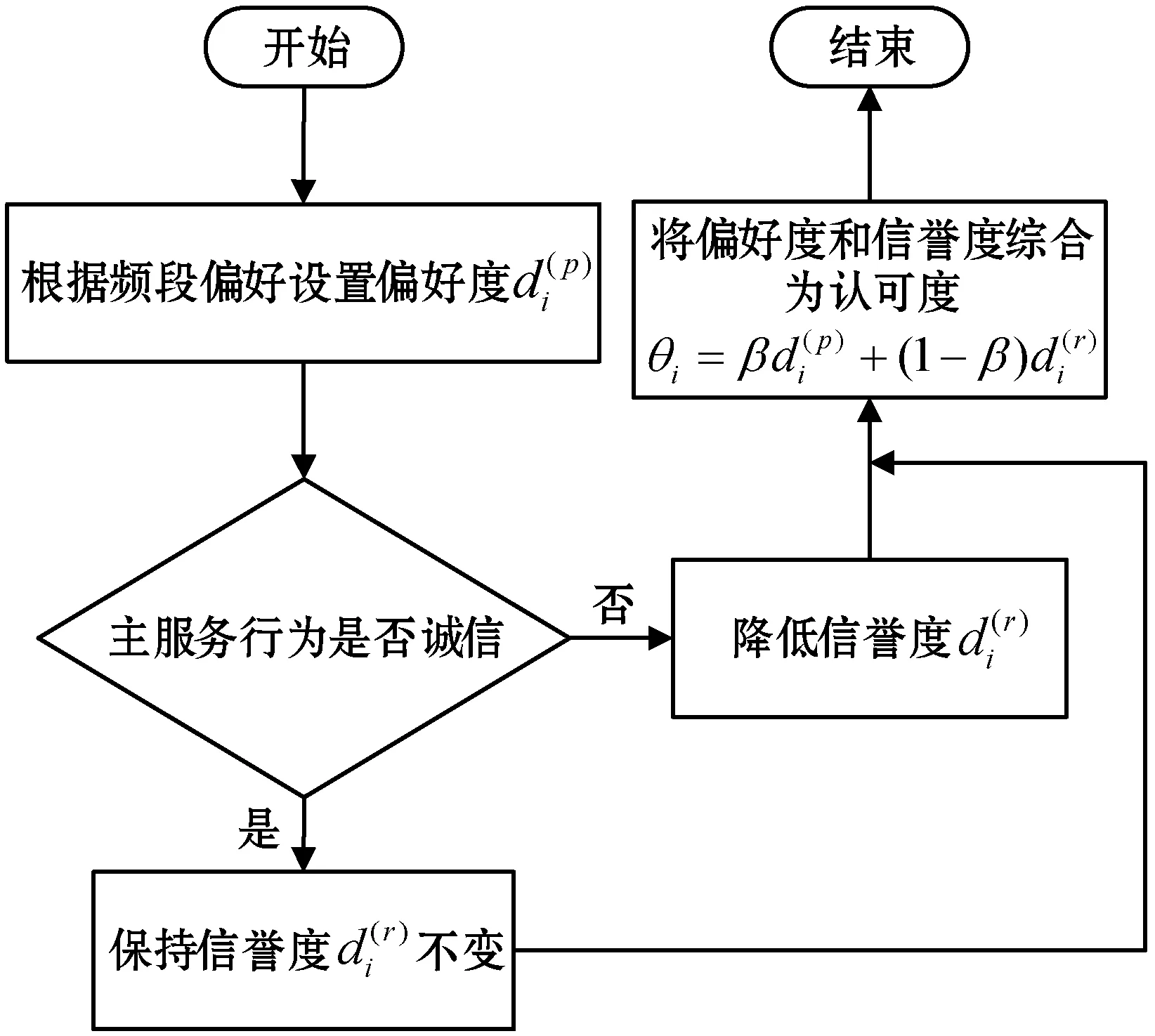
图3 认可度更新机制

以上提出的频谱租赁框架和认可度更新机制同时适用于静态博弈和动态博弈两种情形。

4 动态博弈算法及其稳定性

4.1 动态博弈算法

在静态博弈情形下，各个主服务的策略和利润在彼此间是共同知识，该条件使得各个主服务可以直接做出最佳的策略选择，同时博弈的纳什均衡可以立即达成。然而在实际的认知无线电环境中，由于隐私和非合作等原因，各个主服务之间未必能观察到彼此的策略和利润。由于不具备完全信息，主服务在有限理性条件下无法立即做出最佳的策略选择，而只能根据次服务的频谱需求信息动态地调整自己的频谱定价，以逐步收敛到最佳策略(即纳什均衡价格)。

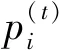
(17)

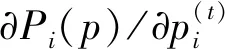
(18)

即：

(19)

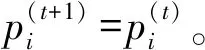
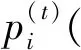
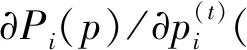
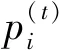
4.2 动态博弈算法的稳定性分析

稳定性对于动态博弈至关重要，本文通过考虑式(17)中自映射函数的雅克比矩阵的特征值来分析动态博弈的局部稳态。

由式(17)得：

(20)

(21)

将式(20)、式(21)代入雅克比矩阵，得：

(22)

纳什均衡点作为不动点之一，当且仅当雅克比矩阵的全部特征值都位于复平面的单位圆内(即|λi|<1)时，该不动点稳定。令矩阵J的所有特征值的模小于1，通过解不等式组，即可得到动态博弈的稳定区域。

5 仿真实验与分析

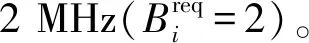
在不同的认可度和信道质量条件下，两个主服务的最优反应函数如图4所示。纳什均衡位于最优反应函数的交点，从图中可以看出，信道质量和认可度均会对其位置造成影响：若信道质量变好，则主服务会提高频谱价格；若次服务对某个主服务的认可度下降，则该主服务会降低频谱价格，而另外的主服务会提高频谱价格。实际上，次服务在更好的信道质量下能获得更高的传输速率，因此频谱需求增加，此时主服务将通过提高频谱价格来谋求更大利润；当某个主服务的认可度下降时，即代表次服务从其购买频谱的意愿减弱，此时该主服务将通过采取降价措施来弥补因竞争力下降所造成的损失，而另外的主服务将通过借机涨价谋求更大利润。特别指出，当次服务对两个主服务均为完全认可(即θ1=θ2=1)时，效用函数退化到原始状态，由于信道质量相同(γ1=γ2)，两个主服务为对称关系，因此它们的纳什均衡价格相等。

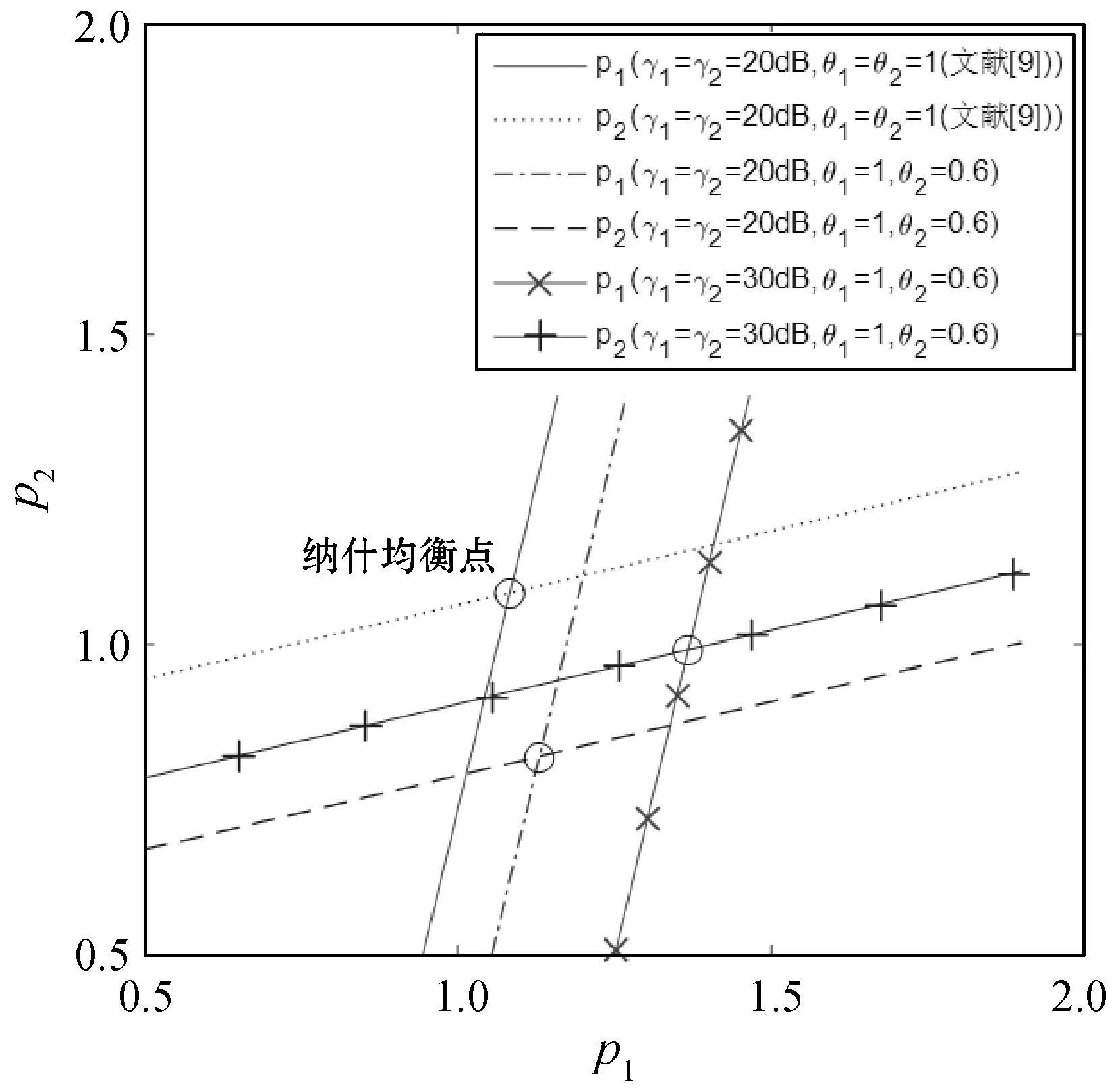
图4 最优反应函数和纳什均衡点

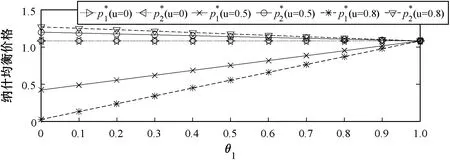
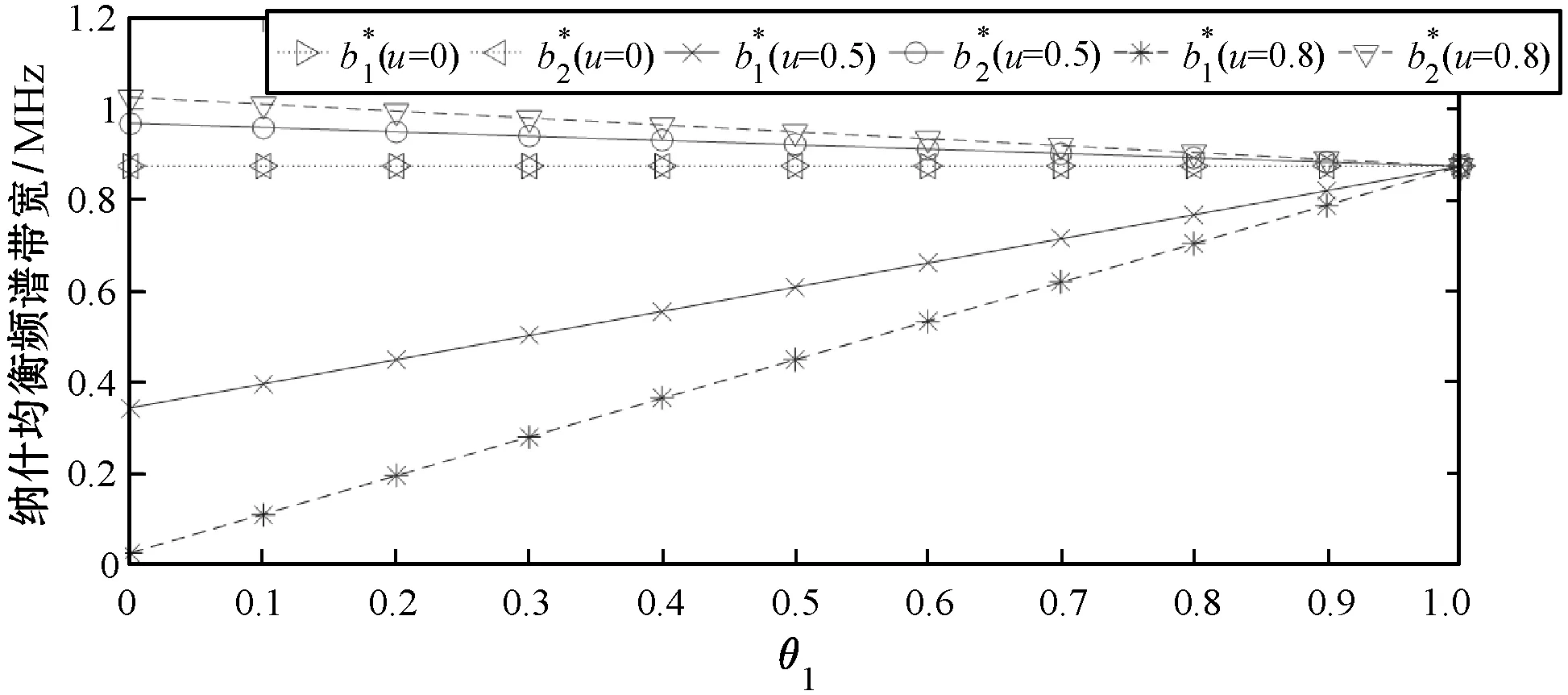
图5(a)反映了单个主服务的认可度连续变化对纳什均衡价格的影响。设置主服务2的认可度固定为1不变，主服务1的认可度从0变化到1，从图中可以看出，随着主服务1的认可度提高，其纳什均衡价格也提高，与此同时，主服务2的纳什均衡价格降低，当主服务1的认可度增大到1时，两个主服务的纳什均衡价格相等。当u=0时，两个主服务的纳什均衡价格相等且保持不变，即此时认可度参数对博弈不产生影响。从斜率可以看出，u的值越大，博弈对认可度的变化越敏感，即认可度参数对博弈结果的影响越明显。与图5(a)类似，图5(b)和(c)分别反映了次服务的纳什均衡频谱带宽和主服务的纳什均衡利润受影响的情况。从图5总体来看，认可度的提高能使相应主服务以更高价格租出更大频谱带宽并获得更多利润，与此同时，认可度的降低将是一种有效的惩罚手段。

(a)

(b)

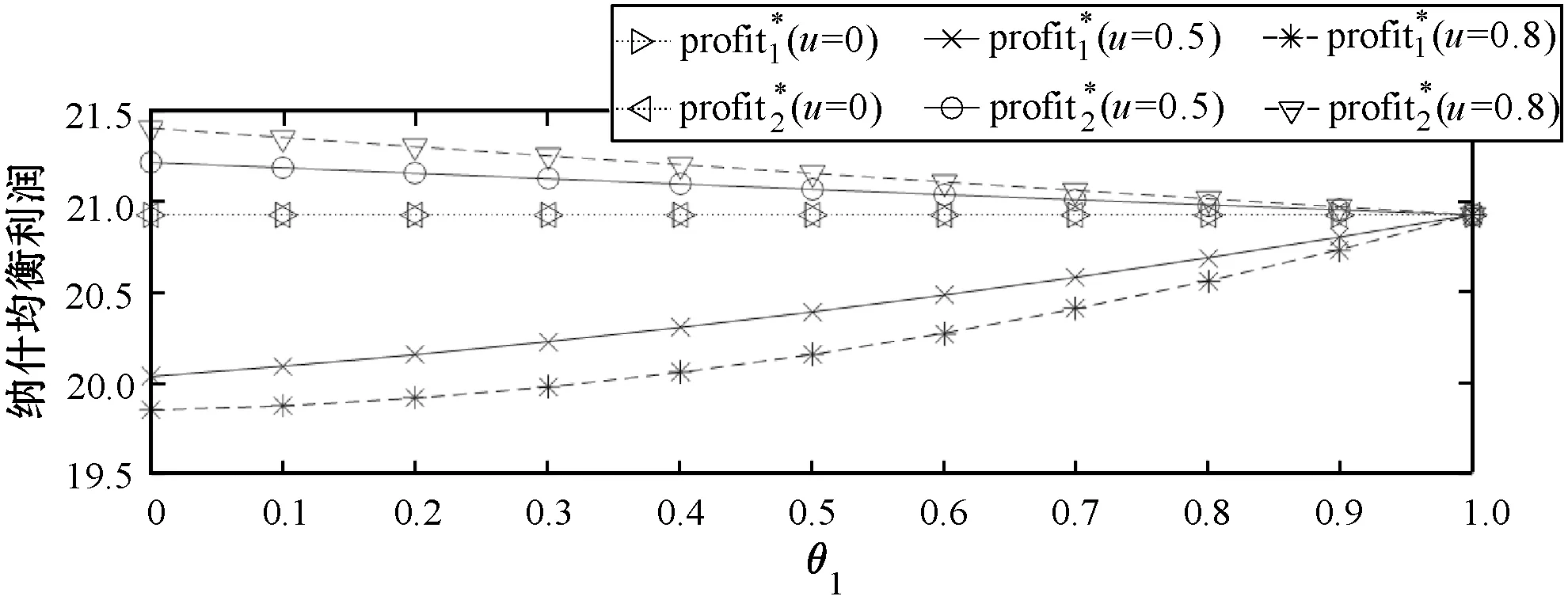
(c)图5 认可度对纳什均衡的影响

图6为两个主服务的纳什均衡利润曲面(u=0.8，γ1=γ2=20 dB)。两个曲面是对称关系，交线在底面的投影表示θ1=θ2的直线，也即(0,0)到(1,1)的连线，连线左侧为θ1<θ2的区域，右侧为θ1>θ2的区域。从图中可以看出，在θ1<θ2的区域，主服务2的利润更高，而在θ1>θ2的区域反之。此外，θ2=1的平面与两个利润曲面的交线即为图5(c)中u=0.8的两条纳什均衡利润曲线，两个结果是一致的。从实际来看，在同等信道质量条件下，认可度高的主服务总是可以获得更多的利润，体现了算法的公平性。

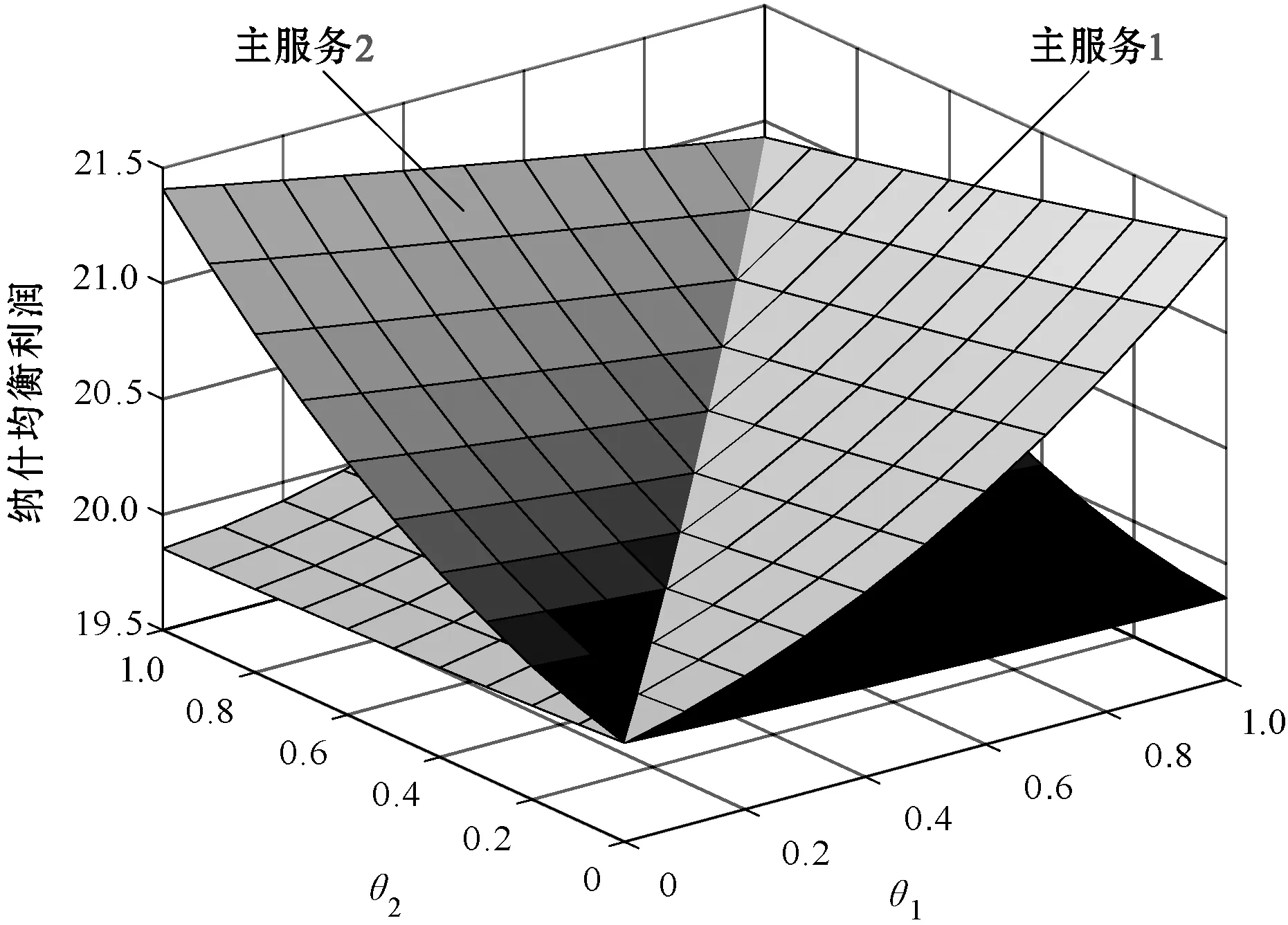
图6 纳什均衡利润曲面

假设在第j-1个算法周期，次服务对两个主服务均为完全认可(θ1=θ2=1)，主服务2在第j个租期中出现提前收回频谱的不诚信行为，导致次服务利益受损，次服务在第j+1个算法周期通过降低信任度对其进行惩罚(θ1=1，θ2=0.8)，在此后的租期中，主服务2又连续出现不诚信行为，次服务每次以0.2为梯度降低其信誉度(0.6→0.4→0.2→0)。图7反映了信誉度对纳什均衡带宽的影响，从图中可以看出，主服务2在几个连续的算法周期中租出的频谱带宽迅速减少，而主服务1租出的频谱带宽缓慢增加，当到达第j+5个算法周期时，主服务2租出的带宽相比主服务1基本可以忽略不计。此外，由于偏好度与信誉度在数值上对认可度的贡献是相同的，因此若将仿真参数替换为偏好度，仍能得到与图7相同的结果。从实际来看，次服务总是从具有更高信誉度/偏好度的主服务处租用更多频谱，这种导向有利于优化频谱共享环境，并促成更加合理、有效的频谱共享结果。

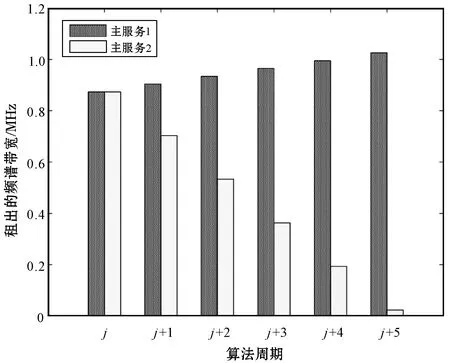
图7 信誉度对纳什均衡带宽的影响

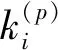
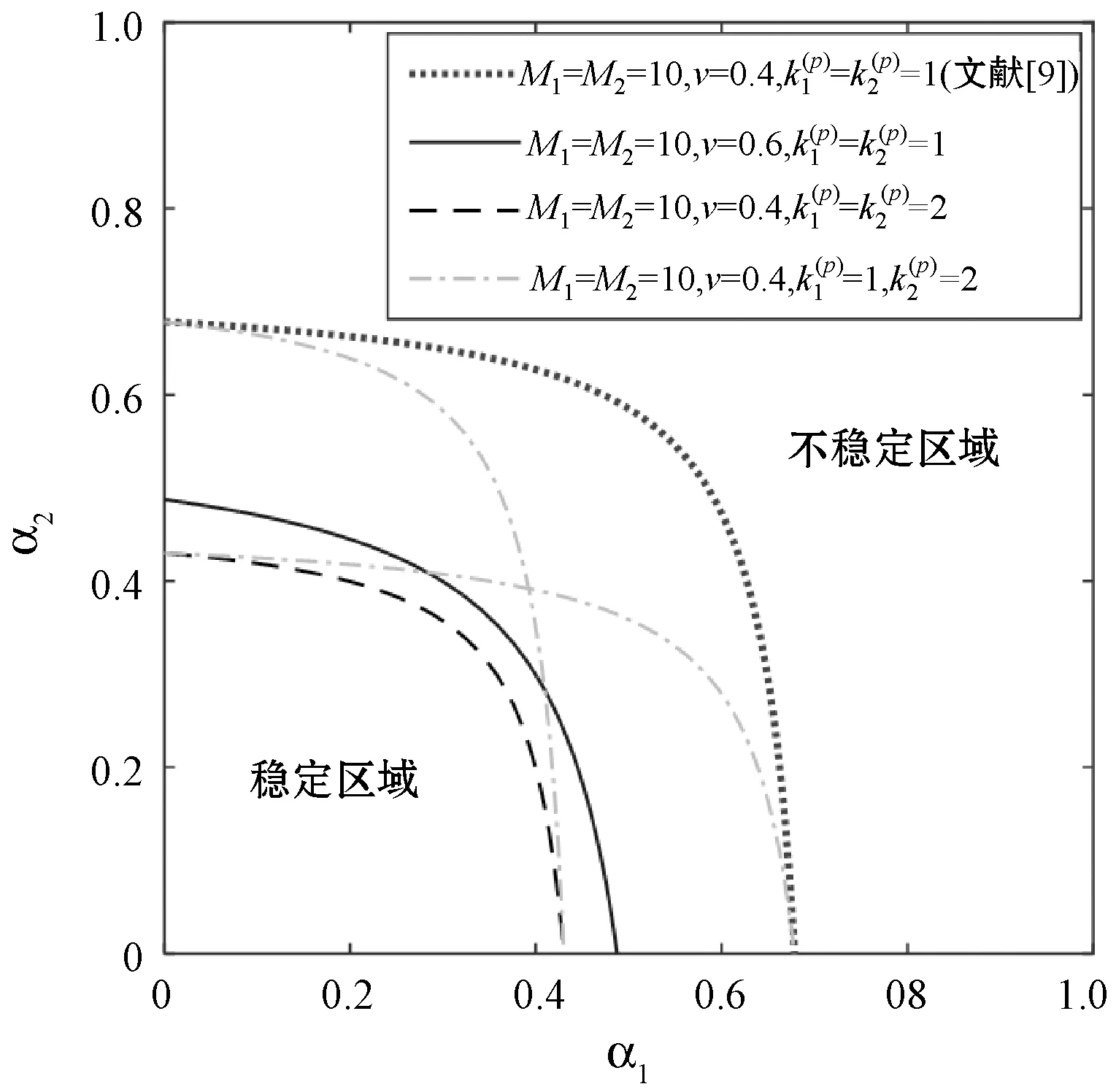
图8 动态博弈的稳定区域和不稳定区域

若两个主服务的认可度θi(i=1,2)分别为1和0.6，则纳什均衡价格分别为1.13和0.82，图9是频谱价格的收敛过程，从图中可以看出，动态博弈最终收敛于纳什均衡价格，并且收敛速度与学习因子αi的取值有关，αi越小，收敛速度越快。合理设置αi的值可以使算法快速收敛，若学习因子过大，则策略调整过程中将出现波动，使得算法收敛速度减慢。

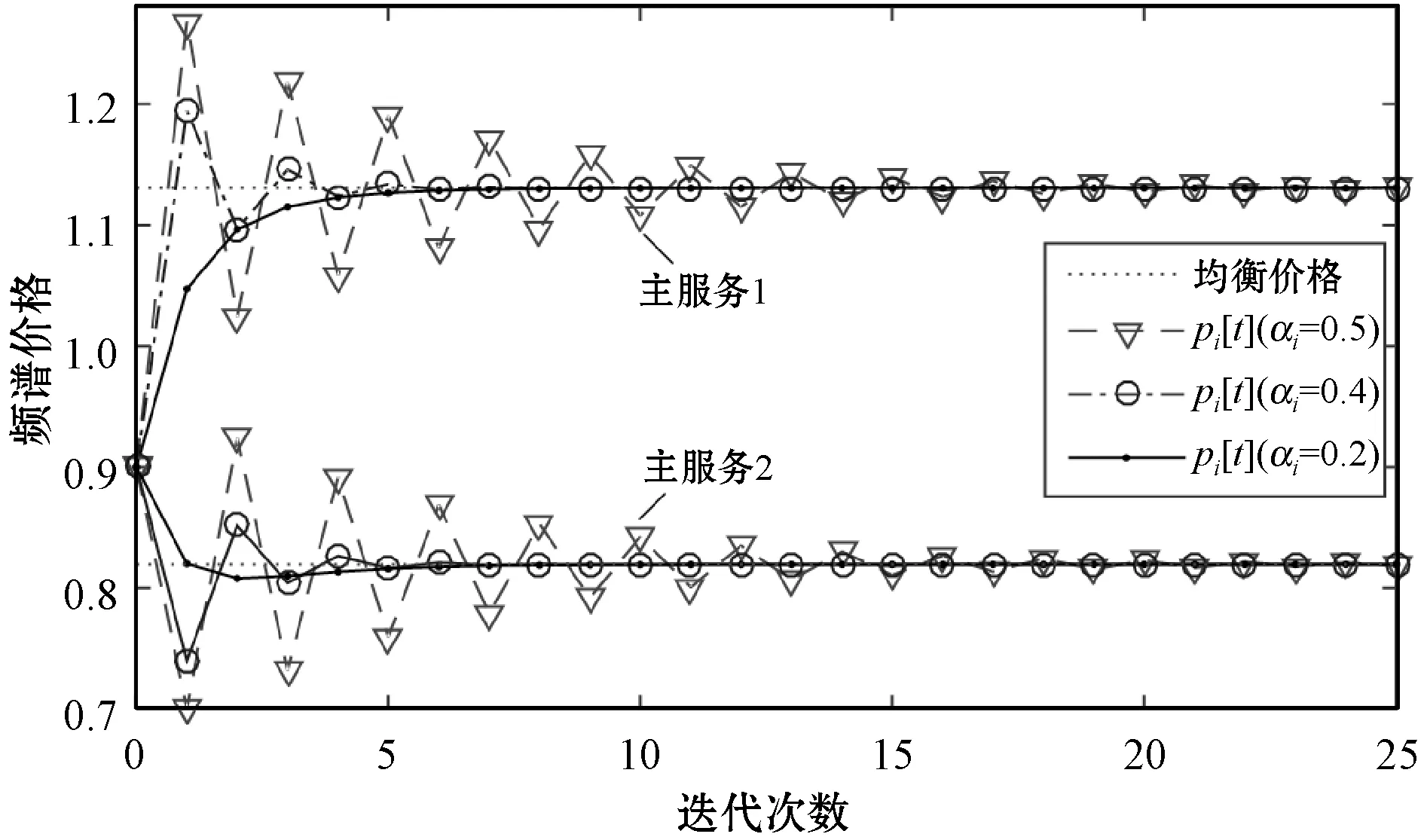
图9 动态博弈的迭代收敛过程

6 结 语

本文针对多主服务—单次服务的认知频谱共享场景，提出了基于认可度的主服务博弈频谱共享算法，并构建了相应的频谱租赁框架。算法中考虑了频谱水平差异下次服务的频段选择偏好和主服务的信誉度，在基于Bertrand博弈的频谱共享模型中引入认可度机制，得到了包含认可度参数(偏好度参数和信誉度参数)的新效用函数，并通过在不同算法周期间动态更新认可度参数来优化频谱共享环境。考虑到在实际的频谱共享环境中，博弈通常难以具备完全信息条件，本文将算法扩展到了动态博弈情形，并对其稳定性进行了分析。仿真实验结果表明该算法能实现更加合理、有效的频谱共享。