举一反三 融会贯通

王华

[摘 要]数学复习课不是“刷题”课，不是试卷辅导课。数学复习课的重心要放在系统地整理单元内容，架构单元知识网络体系上，并要对单元知识进行横向沟通与纵向联系，进而使复习课既有宽度又有深度，同时让学生不仅学会思考，而且能够学会举一反三、融会贯通，能体会到数学的内在逻辑之美、知识之间的简约之美和数学应用的变化之美。

[关键词]圆柱;复习课;思维导图;举一反三

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0059-02

大数学家陈省身曾说过：“数学好玩。”然而对于很多学生来说，学习数学是一件非常痛苦的事。经常能看到一些教师把复习课上成“刷题”课、试卷辅导课。这样机械重复的训练，使学生总有做不完的题，导致数学学习没有灵气、活力，学生只会厌恶数学、远离数学。笔者认为，数学复习课的重心要放在系统地整理单元内容，架构单元知识网络体系上，并要对单元知识进行横向沟通与纵向联系。这样，复习课才会既有宽度又有深度，学生不仅学会思考，能够举一反三、融会贯通，而且能体会到数学的内在逻辑之美、知识之间的简约之美和数学应用的变化之美。下面笔者就以“圆柱”的复习课为例，谈一谈如何上好小学数学复习课。

一、利用思维导图整理单元内容，促进学生形成有效的认知图式

思维导图又称心智图，是一种将人脑放射性思考具体化的方法，是有效表达放射性思维的图形思维工具。有效利用思维导图对单元内容进行整理，有助于架构知识的联系与沟通，有利于帮助学生形成结构化的知识体系，促进学生对知识的理解与记忆。

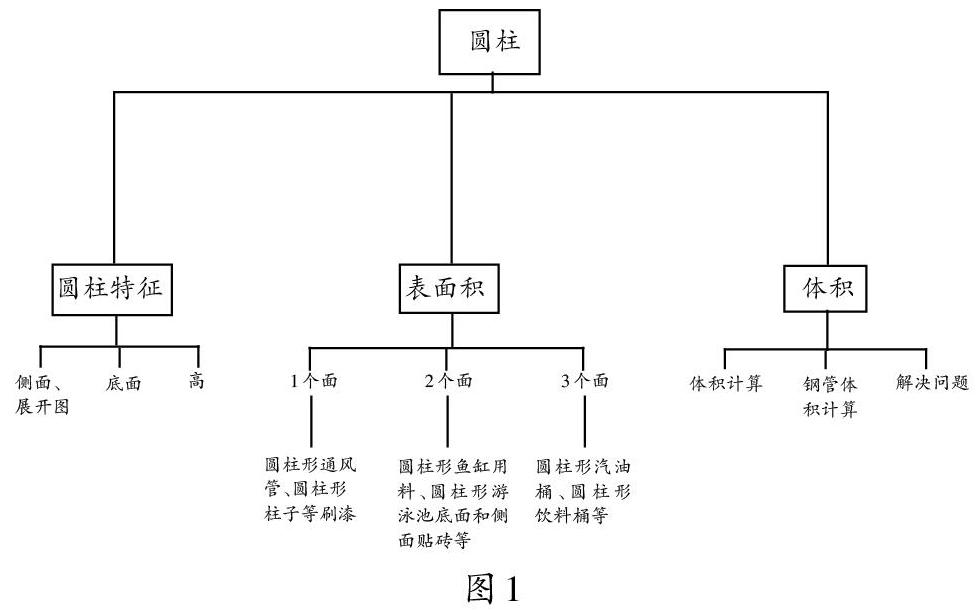
例如，利用思维导图整理“圆柱”这部分知识（见图1）。

这样整理，圆柱的知识框架一目了然。“圆柱”知识主要有圆柱特征、表面积、体积三部分内容，其中对于圆柱的表面积“1个面——2个面——3个面”进行纵向联系与沟通，可促进学生形成完整的认知图式，便于学生将新知纳入原有的认知结构之中。

二、充分应用化归的数学思想方法，帮助学生构建知识体系

虽然数学复习课不是“刷题”课，但做少量的题是必要的，不能为做题而做题，通过深入理解一道题就能联系到相关的内容，这才是做题的初衷和价值。因此，数学复习课要抓住单元知识内容的内在主线，将知识融会贯通。

[教學片段一]复习圆柱的表面积“1个面”。

师：圆柱的侧面积怎样计算？

生1：S侧= Ch。

师：在实际生活中是不是所有的圆柱求侧面积问题都会告诉底面周长和高这两个的值？

生2：不是。可能告诉直径和高或半径和高。

师：若告诉直径和高或半径和高，怎样求圆柱的侧面积？

生3：S侧=πdh=2πrh。

师：我们知道侧面积等于底面周长乘以高，若告诉直径和高，你会怎么想？若告诉半径和高，你会怎么想？

生4：都是要先求出周长，再计算侧面积。

板书：S侧= Ch←周长←直径←半径

通过上述教学可以看出，这是知识的纵向联系，这里应用了匈牙利著名数学家P·罗莎的“化归法”，化归法是一种分析问题与解决问题的基本思想方法，也是学生学会思考、增长智慧的有力抓手。可以借助数学问题解决的多步化归图示进行说明（见图2）。

三、通过知识的横向联系建构模型，促进学生对所学知识能够举一反三

要让学生享受既“有营养”又“好吃”的数学学习，必须教给学生一些数学思想方法，使得学生既能习得基础知识和基本技能，又能抓住数学知识的本质，使学生不仅能融会贯通，还能举一反三。这样的知识建构，才有利于提升学生的学习兴趣，让学生轻松学好数学，为学生的应用意识和创新意识的培养奠定良好的基础。

[教学片段二]复习“圆柱侧面积的应用”。

师（出示题目：一个圆柱形的通风管，底面周长是12.56 cm，高是5 cm，做这样一个通风管需要多少铁皮？）：谁来说一说这道题目是求圆柱的什么？

生1：侧面积。

师：谁来说一说解题的思路？

生2：底面周长乘以高。

师：有了这些条件，我们还能解决生活中的哪些实际问题？

生3：铁皮水管的用料。

生4：圆柱形柱子刷漆问题。

生5：压路机滚动一周压过的路面问题。

生6：只要告诉1分钟压几圈，就可以求出1小时压过的路面的面积。

师：同学们想得都非常好，根据这两个条件就可以解决这么多的实际问题。学习数学就要举一反三，灵活地应用知识解决问题。

……

上述教学环节中，通风管的问题能促进学生积极思考解决生活中的许多类似问题，帮助学生有效构建模型，指引学生如何学习。这样的教学，不仅仅是在教知识，更重要的是在引导学生如何学会学习。

总之，课堂教学是一门学问，作为教师，应时刻思考：每一节课我应该如何教？如何使学生学会学习？好的数学教育、数学课堂教学不是重复呆板的机械训练，不是让学生有“刷”不完的题。学生学习数学，做题是必要的，但所做的题目一定要是典型的、有价值的、富含思想和方法的题，在做题的过程中不仅要会做、能做对，更重要的是学会联系与沟通，能够举一反三、融会贯通。而这才是上乘的数学课堂教学、上乘的数学教育。

（责编 黄春香）