于多元比较中度量速度，借直观感悟助模型建构

代益梅

[摘 要]结合杨悦婷老师执教的新世纪北师大教材“路程、时间与速度”一课，再次认识“度量”，聚焦“速度”，从“度量”的视角进行品鉴与解读，解惑两个“为什么”：“为什么核心词是速度，而不是路程与时间”“为什么要聚焦本质，直观感悟层层建构，而不要更多的模型变式操练”，进而提炼“度量速度”的策略——多元比较、直观感悟等。

[关键词]度量速度;模型建构;比较;直观

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）05-0020-04

一、从“度量”的视角思考：为什么核心词是“速度”，而不是路程与时间？

1.关于“度量”的再认识

参加了新世纪小学数学“悦读”的主题活动——“度量”后，我深深感受到自己的“才疏学浅”和“孤陋寡闻”。原来，我以为“拿尺子量长度”“拿量杯测容积”“数标准方格量面积”……这些表面操作行为就是度量。而经过密集式的学习，翻阅了一些资料，我重新理解了“悦读”活动中 “度量” 的含義与英文measurement的含义比较一致——指计量长短、容积、轻重等物体属性的统称，以及“度量”的本质在于“表现事物某些指标的顺序”，而且还可以大体分为数量度量（通过抽象得到其度量单位）和工具度量（借助工具得到其度量单位）。更令我惊讶的是“路程、时间与速度”一课归于“工具度量”的内容，竟然也可以从度量的视角来解读和建构这堂课。

2.关于“速度”的再挖掘

为了使学生理解起来更加容易，课程标准和教材编者设立了一个大前提：默认小学阶段的路程模型中，研究的物体运动是直线运动，且初学时暂不考虑路程的方向，把路程作为一个标量而不是矢量（位移）;把物体运动速度看作均匀的;把时间视为绝对的，不涉及观察者的角度等。在以上这些大前提下再从度量视角出发：“路程”的本质就是度量物体作直线运动轨迹的长度;“时间”的本质就是度量事件过程的长短和发生的顺序;“速度”的本质就是度量物体运动的快慢。

3.关于教材的再解读

九年前，我在一次成都市数学赛课中参与了 “路程、时间与速度”一课的打磨，贡献了一个“金点子”——借助归纳法（8千米/秒，8千米/分，8千米/时）抽取速度的描述性定义：物体在单位时间内所行驶的路程就是速度。时隔数年，我发现自己当时对这一课的解读实在很浅薄，一味追求“比较两辆车谁跑得快”的方法多元化，简单粗暴地提炼出速度的计算公式后，就借助习题推导出另外两个关于时间和路程的衍生公式，没能直接从“度量”视角来深度解读这一课。

史宁中教授提到：在小学阶段的数学教学中，至少需要考虑两个模型，其中一个就是“路程模型”，既然模型以“路程”来“冠名”，为什么各个版本的教材在编排路程模型的内容时几乎都围绕“速度”这个核心词来切入？再者，在这个“路程（距离）=速度×时间”的乘法模型中，就单纯的物理意义而言，变化的只有“时间”，为什么不抓这个“时间变量”来引入？在研读教材的过程中，我找到了答案。

以新世纪北师大教材第79页“路程、时间与速度”为例，教材首先是结合三个动物竞走的情境，提供颇有意义的三组数据，让学生猜谁走得最快。这里一开始就提问“谁走得最快？”，是紧扣“速度”的本质——“速度度量物体运动的快慢”来设计的，让学生利用多种策略比较快慢的同时初步感知速度的本质，体会竞走运动的快慢与时间和路程有关。

在铺垫之后，紧接着抛出难点问题——竞走路程和时间都不同的情况下，如何比较谁走得快（松鼠和小兔比快慢）？通过求两只动物的“平均速度”来比较快慢，引导学生用除法计算的结果来比较，契合前面提到的路程模型的假设大前提——物体作匀速运动，并得出求速度的公式。

再通过速度的度量单位构成，以及渗透生活中常见的速度，学生进一步体会到速度与路程和时间的关系，更深刻地认识到，路程和时间是可以通过度量工具进行直接度量的;而速度则是间接度量，通过路程和时间这两个物体运动时相匹配的属性的一次度量之后，来度量运动时的快慢。或许正是因为“速度”这个物体运动属性的复杂性、丰富性和关联性，且“时间”这个概念学说不停歇争论的矛盾性，对于“路程模型”的内容，编者均从“速度”切入（图略）。

在查阅教师执教相关内容的教学实录过程中，我从成都市泡桐树小学杨悦婷老师的教学中品出其蕴含“度量”的芳香，下面节选其中二三精彩环节展开论述。

二、从“度量”的视角品鉴与解读：为什么要聚焦本质，直观感悟层层建构，而不要更多的模型变式操练？

在杨老师的课堂中，每个看似“简约”的设计背后都饱含精巧的思维布局。不论是从头到尾的逐层建构模型，还是关键之处的几何直观感悟，从“度量”的角度细细品鉴，她整堂课无时不在贴近“速度”的本质和理解路程模型中三者的关系。

1.于微视频中触摸“速度”的激情

在整堂课的教学中，杨老师均借助信息化手段制作和播放微视频，运用智慧HI-TEACH软件的反馈功能和大数据分析，精准把握学情，逐层建构路程模型。

【片段1】将一段含有6个速度的微视频《你的第一感觉是什么？》作为奖品奖励给全体学生。

师（播放微视频，略）：看了这段视频，你的第一感觉是什么？

生1：赛车开得很快。

师：说得很好，用了一个字“快”。

生2：变脸很快，14秒变了28张脸。

师：也说到了一个“快”。请举例让你印象最深刻的东西。

生3：乌龟爬得非常慢，1分钟才爬1米。

师：你们说到的快和慢，其实是什么？

生（齐）：速度。

师（揭题）：今天我们就一起来学习速度。在生活当中，物体的快慢可以用速度来表示。

解读——微视频：让“速度”亲民，让“度量”入心

在开课环节，一段含有6个速度的微视频《你的第一感觉是什么？》让学生真切感受到生活中处处有“速度”，速度很親民，同时也在捕捉学生发言的关键字“快”和“慢” 中顺势揭题：物体运动的快慢，可以用速度来度量。微视频中的6个速度不仅有快速度，有慢速度，而且每个速度均配了一句话，比如“1小时行驶300千米”“1分钟爬了1米”等，每句话介绍速度时，都出现了跟它相关联的时间单位和路程单位，学生在观看了微视频后就能够初步感知到度量每一个“速度”，都涉及“千米、米”等这些“路程”相关量和“时、分、秒”等时间相关量。这里要特别提出，微视频里还有一个特殊的“变脸速度”——“14秒变28张脸”，严格意义上来讲，这不直接属于理工学意义上的“速度”，可以看作从这个路程模型衍生的“工程问题”，度量的是工效，即工作速度。

同时，信息化技术的应用，激发了学生的学习兴趣，吸引了学生的注意力，让数学学习更亲民，让学生乐于学习数学。

2.于比较中逐层完善路程模型的建构

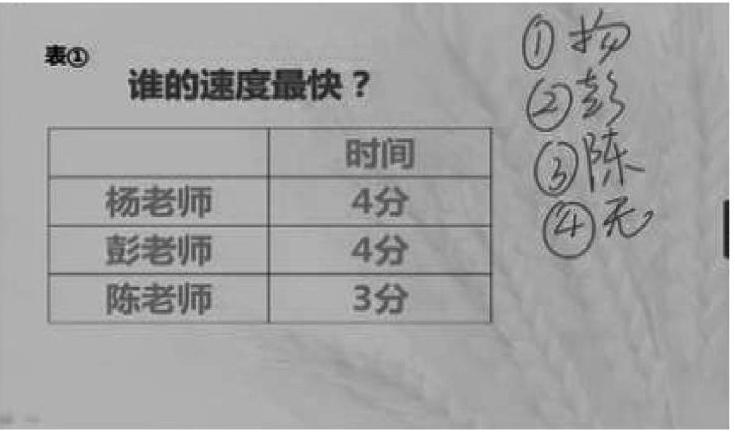
【片段2】把教材的动物竞走比快慢的主题图，调整为三位老师（杨、彭、陈）比较速度，并请全体学生投票。首先，只出示表格中三位教师所用的时间，请学生比较后给速度快的投票。

师：谁的速度快？①、②、③分别对应杨、彭、陈老师，④是“无”，请投票。（绝大多数学生选④）

师：能说说为什么选择④吗？

生1：因为它们只有分钟，没有多少米，所以我无法判断。

生2：我听懂了生1的发言，上面给出的三位老师的数据只有时间，没有路程，所以并不知道他们走了多少米。

师：学会倾听且能将其转化成自己的语言，很棒。有没有更简洁的说法？

生3：我想说缺少了一个“成分”，那就是路程。

师：如果需要知道“速度”，需要几个“成分”？

生（齐）：两个。路程和时间。

师：速度与两个量都有关，它与我们之前说的质量的轻重、距离的长短不一样，要刻画速度的快慢，需要知道相应的路程和时间。

师（出示三位老师相对应的路程信息）：现在能判断了吗？

（学生小组合作：6个组用除法计算;1个组用线段图，2个组用简要文字）

师：用得最多的是三个除法算式，请第六组具体说一说。

生4：路程就相当于我们原来学的总数（总量），时间就相当于份数，速度就表示每一份数。

师：那速度就等于什么？

生4：速度就等于路程除以时间。

师：有补充吗？

生5：也就是总数÷份数=每份数。

（生4继续解释三个除法算式中每个数量所表示的意思）

师：第六组发言中有没有值得我们借鉴和学习的地方？

生6：他们化新为旧了，把今天学习的路程变成了之前学的总数，把时间变成了份数，把速度变成了每一份数。

师：非常好，善于倾听和评价。那速度到底是怎么得到的呢？

生（齐）：路程÷时间=速度。

师：这里的60、70、80又分别代表了什么？

生7：分别代表他们一分钟走的路程。

（第九组分享他们的比较策略：首先，发现彭老师和陈老师走的路程一样，彭老师用时比陈老师多，通过这两位老师的对比之后淘汰彭老师，就只剩下杨老师和陈老师;然后，通过杨老师走的路程和他所用的时间，计算出杨老师每分钟走70米，通过陈老师所走的路程和他的用时，算出陈老师每分钟走80米;最后，由对比得出陈老师的速度是最快的。）

师：简而言之，路程相同就比时间。时间用得短，说明速度怎么样？再看看杨老师和彭老师所用的时间。

（学生发现杨老师和彭老师用的时间相同;教师引出比较策略：时间相同比路程）

师：好！在比较快慢时，除了利用这样一个关系式直接算速度，我们还可以根据路程相同比时间，时间相同比路程来看快与慢。可是，无论用什么方法，都说明了速度与路程、时间都有关。

【片段3】在深度分享了学生对“速度”的几何直观理解之后，以比较两个10米来引出速度单位的学习。

师：你认为谁的速度快？

生1：我选③，因为它们两个数据都一样。

生2：我选①，因为100÷10和30÷3中，100这个数据表示的路程要大一些。

生3：我选④，因为我不知道甲和乙的单位是不是一样的。

师（出示速度的“主人”）：我现在告诉你，甲是博尔特的速度，乙是蜗牛的速度，根据常识，哪个速度快？第一个10米表示什么？第二个呢？

生4：甲快。第一个10米表示每秒跑10米，第二个10米表示每小时爬10米。

师：此10米非彼10米。刚刚没有告诉我们的是什么单位？

生5：时间单位，所以刚刚应该选④。

生6：假如说这个比赛是吃苹果，苹果都一样，那么博尔特每秒吃10个，蜗牛每小时吃10个;如果都吃5小时，博尔特5小时能吃3000多个，蜗牛才吃50个。

师：你的想法特别好。速度的单位仅仅用米、千米这样的路程单位显然不足以表达。速度单位的共同点是什么？

生7：它们都是一个标准的，比如1秒、1分、1时这样的单位时间。

师：这个速度单位里面包含了什么单位？

生（齐）：时间单位和路程单位。

师：我们再次印证了速度与路程和时间的紧密关系，所以这个速度的单位是多么特殊啊！

解读——多元对比：没有对比就没有“伤害”，没有对比就没有“模型建构”

为了建构“路程模型”，聚焦模型中的“速度”描述性概念的习得，整堂课从头到尾都在进行大量的、渐进式的、有梯度的“比较”，并总结出灵活实用的“比较策略”。特别突出的是以下几个方面：

（1）挖坑：主题教学探究时，一开始只呈现三位老师的时间信息，就要求学生比較他们的速度。少部分学生掉进了“坑里”，绝大多数学生非常明确，这样的比较缺少“成分”，至少需要两个“成分”，仅有时间是不够的，所以无法比较，不能度量出谁的速度快。

在这里，杨老师的过渡语运用得十分巧妙，且紧扣主题：“速度与两个量都有关，它与我们之前说的质量的轻重、距离的长短不一样，要刻画速度的快慢，需要知道相应的路程和时间。”既密切关联以前学过的度量物体轻重的属性——质量，度量物体长短的属性——长度，又轻松过渡到当堂课速度的学习中——比较速度的两个“成分”。

（2）渐进：杨老师先补充完三位老师分别与时间对应的路程信息，然后开放性设问“谁的速度快？”，并先请小组代表分享最常见的主流方法——用除法算式求速度再比较。 “路程就相当于我们原来学的总数（总量），时间就相当于份数，速度就表示每一份数。”这个发言的学生已经能够把之前学过的“总量=份数×每份量”这个模型套用在路程模型上，并且进行逆运用，而且说理清晰，实在难能可贵。学生在比较中能够“化新为旧”，化归思想的渗透不可小觑。

（3）策略：在师生共同总结出 “速度=路程÷时间”这个模型，并用其比较速度的快慢时，第九组学生以表格中的数据为例，归纳梳理了两条比较策略：路程相同时比较相对应的时间;时间相同时比较相应的路程。杨老师再次渗透速度的本质属性：“无论用什么方法，都说明了速度与路程、时间都有关。”因为速度具有不可直接度量的属性。

（4）悬念：为了引出速度单位，杨老师又以比较甲乙两个10米的速度入手，仍有一部分理智型的学生始终坚持无法比较。当甲乙两个速度的“主人”现身后，一位学生的补充令人拍案叫绝：“假如说这个比赛是吃苹果，苹果都一样，那么博尔特每秒吃10个，蜗牛每小时吃10个;如果都吃5小时，博尔特5小时能吃3000多个，蜗牛才吃50个。”尽管他的表述太“小看”博尔特了——错估成了3000多个，但是他对速度、速度单位的理解，甚至在速度单位间的换算上，有一种惊人的、深入浅出的数学直觉。在学生学习了速度单位、写速度单位、理解速度单位后，杨老师继续引导：“速度单位的共同点是什么？”再次印证了速度与路程和时间的紧密关系。

整堂课的主体合作探究环节在比较中开始，也在比较中结束，尽管“消耗”了“大把时间”，但是时间花得值，路程模型在各种比较中逐渐抽取出来，并深入“人心”。

3.于线段图中凸显几何直观的妙用

【片段4】展示第二组的画线段图方法

师（出示课件）：第二组虽然画得不够完整，但是与杨老师的想法不谋而合，大家看了有什么想法？

生1（在白板上勾画橙色线）：把每个老师一分钟走的线段移上来作比较，这条线是彭老师的，另一条是陈老师的，中间这个是杨老师的。陈老师在最前面，说明速度最快;彭老师在最末尾，说明速度是最慢的;杨老师在中间，不快不慢。

师：我从生1的发言当中感受到他的方法和别人的不一样，他没有写除法算式，而是直观地比较代表速度的线段。那么这样的一段就是什么？

生（齐）：一分钟走的路程。

师：我们借图说话，不仅可以直观地看到一分钟谁走得快与慢，而且再次说明了速度确实与路程和时间都有关。

师：求速度为什么一定要用除法？透过现象看本质，想一想除法的意义。

生2：除法的意义就是把一个数平均分成几份，且每份都相等。

师：以杨老师为例，把280平均分成4份，每一份就是杨老师每一分钟走的路程……

解读——几何直观：让参与速度“度量”的元素可视，打通“速度”的“任督二脉”

在解决“三位老师谁的速度最快？”这个问题上，第二组采用了画线段图的方法化抽象为形象直观。以三位老师的路程作为整体线段，按时间多少平均分为相应的份数，取各条线段中的一份代表各自的速度，再上移重叠比较，线段长的速度就快，反之则慢。这不仅解决了速度的比较问题，学生还在杨老师的追问下沟通了速度与“除法意义”的联系：“求速度为什么要用除法？”再次沟通 “总量÷份数=每份数”的模型与路程模型的关联，在头脑中刻下深深的印象：要度量速度，必须先打通路程与时间这两个任督二脉。

纵观整堂课，没有琐碎的小问题群，只有画龙点睛处的深度追问;没有形而上的面面俱到的大包围，只有直指速度内核的概念及模型建构。这一切的基础，都得益于杨老师团队扎实的教学功底、深厚的理论储备和博大的育人观。

（责编 金 铃）