振动频域特性与时域测量的分析

李潮锐

(中山大学 a.物理学院；b.物理国家级实验教学示范中心，广东 广州 510275)

在近代物理实验课程中，微波(射频)电子自旋共振和连续波核磁共振实验都使用(永磁体+)稳恒磁场、(周期调制)扫场和(偏振)电磁波(即光子)激发等相似功能的实验装置，但所显示的实验结果却明显不同:前者可观测电子自旋共振吸收峰形，而后者则获得核磁共振尾波[1]；当采用李萨如图表示时，前者的物理图象更清晰，而后者却变得更模糊. 在实验课堂上，通常结合振动频域特性和共振弛豫时域测量的远程实验实时演示[2]，详细分析磁共振实验的物理原理和技术原理. 为了使课堂讨论更加深入，还通过(固态样品)电子自旋共振和(液态样品)核磁共振的频域微分测量辅助课堂教学[3-4]. 尽管在合适实验条件下两者可获得相似的频域实验结果，但是依然难以直观展示磁共振实验测量的关键物理原理,甚至还可能对频域与时域测量的物理关联产生新的疑惑. 事实上，(核)磁共振原理可采用简谐、受迫、共振和阻尼等振动分析的唯象描述,因此，振动实验物理分析是透彻讲解(核)磁共振实验原理的基础. 教学经验表明，通过振动频率特性、受迫、共振和阻尼时域测量等实验事实，结合课堂(远程)实验演示和实时数据分析结果，可有效地帮助学生理解(核)磁共振原理和实验现象，更为后续学习脉冲核磁共振及成像分析提供清晰的物理思路. 本文通过音叉振动频域特性与共振时域测量物理分析，在理论和实验课堂上讲解磁共振原理的教学实践，展现属性关联的物理实验(和理论)课堂教学方法.

1 实验技术方法

实验主体装置是上海复旦天欣FD-VR-B受迫振动与共振实验仪，该设备利用电磁感应原理由驱动线圈和接收线圈分别对音叉实施振动激励和获取响应信息. 固纬APS-1102A电源工作在AC+DC-SYNC模式为驱动线圈提供励磁电流，使用中大科仪双通道锁相放大器OE1022D分别测量(由接收线圈输出的)音叉振动信号和驱动励磁电流(电压)的幅值与相位，且由两者相位差得到振动响应相对于驱动激励的相位. 使用NI USB-6003数据采集卡工作于10 kHz采样率测量音叉振动的时域数据. 由双路继电器实现音叉振动信号频域与时域之间切换测量. 普源DG4162信号发生器为APS-1102A和OE1022D提供同步参考信号. 计算机通过USB接口对实验系统实施测控操作和数据采集分析，同时可以实现互联网远程(跨校区)实验演示辅助物理课堂教学.

2 实验结果及分析

2.1 音叉振动的频率特性

图1为音叉振动速度幅值及其相对于驱动力相位差随频率变化. 根据振动测量传感技术，文献[5-7]已详细分析并确认电磁感应接收线圈输出反映了音叉振动速度. 由于感生电动势和音叉两臂相向运动都产生π相位差，在低频端启振时振动速度相对于驱动力相位超前π/2. 由图1可得知，音叉共振速度幅值最大处频率，即共振频率为236.16 Hz，其相位变化与文献[8]一致.

图1 音叉振动速度幅值和相位的频率特性

音叉振动速度的实部和虚部频率特性如图2所示，可见音叉共振速度具有磁共振或者LC谐振[9]相同的吸收和色散规律. 由于激励线圈和接收线圈(也包括空气)阻尼作用，音叉共振峰具有一定频率宽度，而非δ函数峰型. 理论分析表明，共振峰频谱展宽随阻尼增强而增大[8].

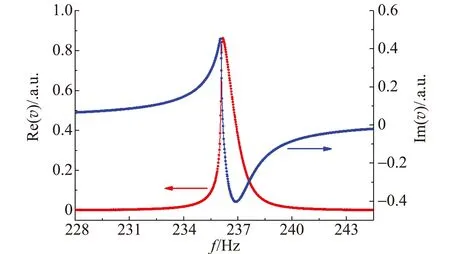
图2 音叉振动速度实部和虚部的频率特性

2.2 阻尼振动分析

利用电磁感应激励和测量响应信息的实验技术方法也影响了音叉振动的频率特性. 激励线圈和接收线圈的磁芯对音叉双臂都产生吸引力，且与音叉振动恢复力反向. 在音叉振动(微小)位移范围内，可以认为磁芯吸引力近似线性变化，等效于减弱了音叉的劲度系数[10]. 随着磁芯逐步靠近音叉臂，(等效)劲度系数逐渐减小，因而音叉共振频率向低频端移动. 另一方面，音叉振动引起线圈磁通量变化，这正是获取振动信息的技术原理. 根据楞次定律，闭合回路中感应电流的方向，总是使得它所激发的磁场来阻碍引起感应电流的磁通量的变化[11]. 或者认为，线圈感生电流所产生的磁场是为了抵抗与它赖以存在的磁通量变化. 同理可知，线圈感生磁场对音叉也存在作用力. 由于感生电流正比于磁通量变化，即音叉振动速度，因而感生磁场强度也正比于音叉振动速度. 由此可见，音叉所受感生磁场力与音叉振动速度成正比，这正是振动阻尼力项.

在振动(微小)位移范围内磁力变化近似线性，可认为两侧线圈感生电流增大音叉振动阻尼系数. 随着磁芯逐步靠近音叉臂，音叉(等效)阻尼系数逐渐增大. 为便于比较，实验全程保持驱动线圈励磁电流(电压)有效值相同.

图3为音叉振动速度实部(吸收的)频率特性随音叉臂与线圈磁芯间隔变化情况. 图3中每个共振吸收峰处标示了所对应的音叉臂与磁芯的距离(单位为mm). 可见，当音叉臂与磁芯间距逐步增大，音叉共振频率向高频端移动，而其共振吸收峰频宽逐渐变窄. 音叉共振频率随磁力变化规律与文献[10]结果一致.

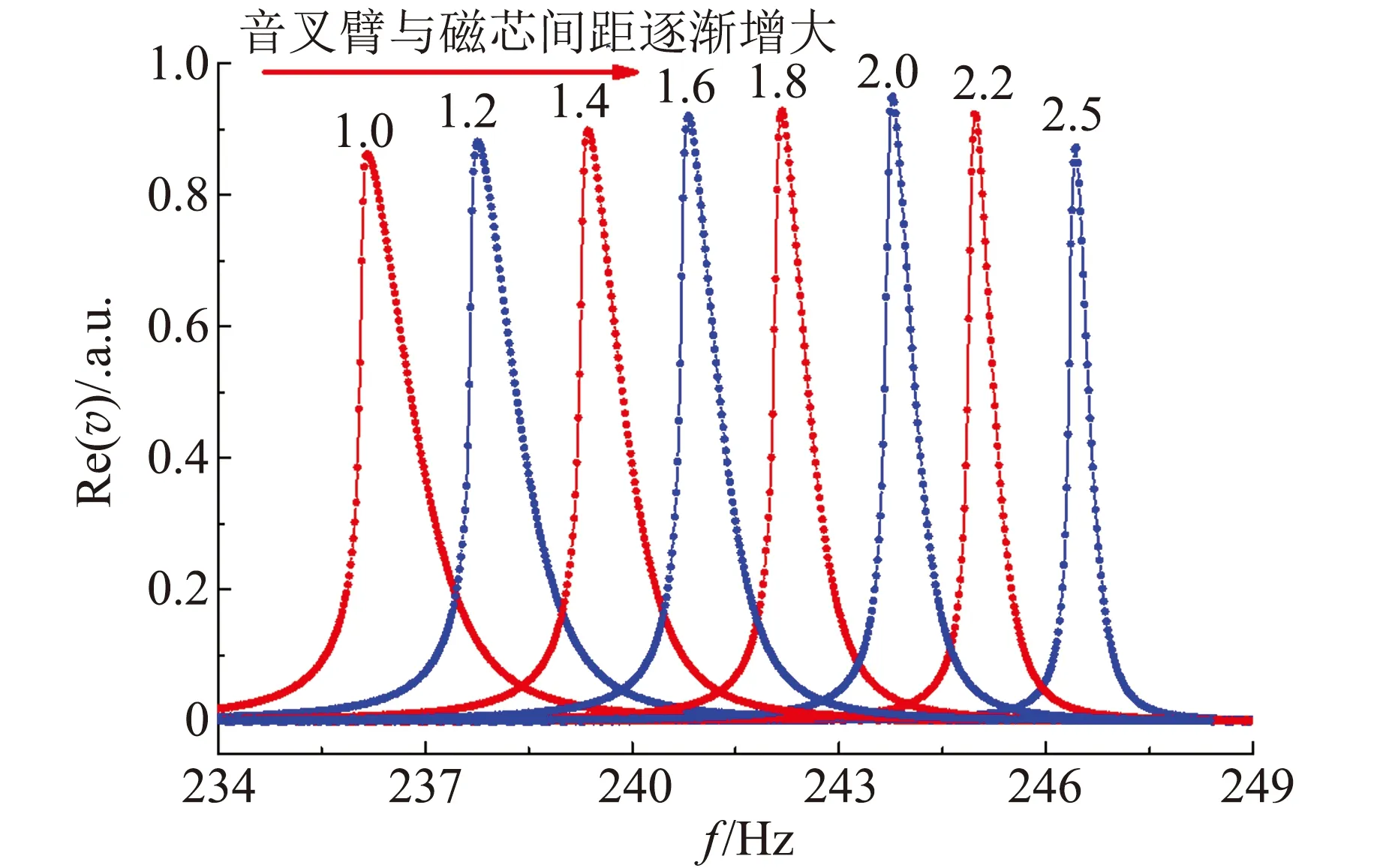
图3 不同阻尼振动速度实部的频率特性

2.3 共振弛豫分析

在驱动力作用下，音叉产生同频受迫振动，且在某特定频率处达到共振. 一旦撤除驱动力，音叉振动随之逐渐减弱，直至恢复静止状态. 这一振动衰减过程可采用指数衰减函数描述，且由衰减时间常量或弛豫时间表征其物理属性.

图4为音叉臂与磁芯间隔约1.0 mm时共振弛豫的时域测量结果，弛豫时间为0.425 7 s. 图中小图为时间轴放大所见信号周期变化，其频率即为音叉振动频率. 图4时域测量数据记录了撤除驱动力后音叉振动随时间衰减过程，可采用

A=A0e-t/τsin (ωt+φ)

(1)

描述，其中，ω和φ分别为音叉振动频率和初相位，τ为音叉振动弛豫时间. 若取每周期峰值所得的振动衰减包络线数据，则可由

A=A0e-t/τ

(2)

得到振动弛豫时间τ.

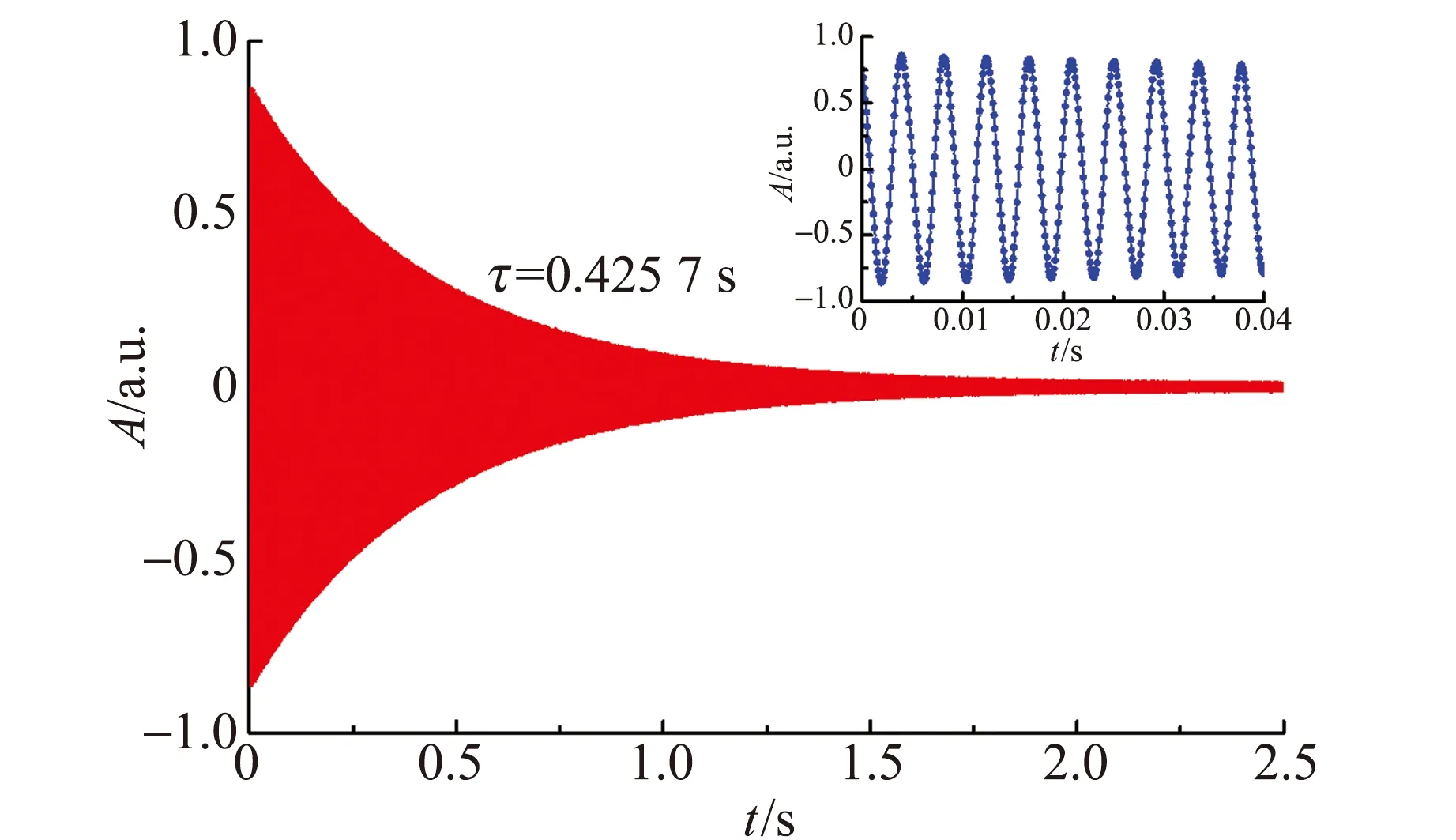
图4 共振弛豫的时域测量结果

图3中不同阻尼情形共振衰减的时域测量分析结果显示，共振弛豫时间τ随阻尼减弱而延长. 使用式(1)或式(2)得到相同的实验结果. 为简化数值计算，采用式(1)分析，可考虑ω为已知量；选用式(2)拟合时，可利用峰点的周期特性.

2.4 共振弛豫与频谱展宽

综合上述分析可知，共振频率展宽和弛豫时间都与阻尼系数有关. 外界驱动(激励)引起音叉同频受迫振动，其本质就是(能量)激发的过程. 换句话说，音叉静止状态是基态，受激(受迫)振动即为激发态. 由此可见，共振频谱(展宽)记录了激发态能级的能量分布(宽度)，而振动衰减时间常量描述了系统从激发态返回基态的弛豫过程. 图3不同阻尼情形的音叉共振频谱展宽(半高全宽)Δf及对应共振弛豫时间τ关系如图5所示.

由图5可见，对于确定体系，共振(吸收)谱宽(半高全宽)与所对应的共振弛豫时间倒数可近似为线性关系，即图5中蓝色直线. 针对音叉振动还可发现，共振谱宽与弛豫时间不成反比关系，明显偏离了图5中红色直线. 上述实验结果表明，随着阻尼增强，共振频谱展宽增大，而共振弛豫时间缩短，且在实验范围内满足Δf·τ<1. 激发态是不稳定态，除非维持不间断激发(受迫)作用，否则最终将返回基态. 基态是稳定态，其弛豫时间趋于无穷；或换个角度说，基态能级展宽趋于零.

图5 共振频率展宽与弛豫时间关系

基于音叉共振的频域和时域独立测量结果，实验上两者存在物理性质关联. 如图4所示，音叉共振时域信号具有明确的周期性，可通过傅里叶变换得到对应的共振频域信息[12]. 图6为采用离散傅里叶变换(DFT)方法，由共振弛豫的时域测量数据得到共振(吸收)频域谱.

图6 DFT所得不同阻尼共振频域谱

与图3相比，图6分析结果虽可得到相同共振频率和近似相等的吸收峰展宽(半高全宽)，但频谱峰幅值却明显不同. 对于完全复制的周期函数(过程)，傅里叶分析可以仅考虑单周期贡献，且通过单周期归一化得到频谱. 对于非完全复制的周期函数(过程)，傅里叶分析必须计及所有贡献周期，因此每一频率DFT数值都与周期数量有关. 尽管归一化体现了频谱分布的概率涵义，但由于不同过程的归一化因子不存在关联，不同实验条件之间的频谱分布各自独立，因而频谱幅值不具备可比性. 对于单峰频谱，峰窄而高，或宽而低. 尽管图6分析结果与图3实验测量的频谱幅值有明显差异，但频谱峰中心频率及其频宽(半高全宽)等参量一致反映了共振的物理属性.

3 结 论

实验测量了音叉振动速度幅值和相位的频率特性，得到共振吸收和色散的频域特征. 通过逐渐增大线圈磁芯与音叉臂间距，频域测量可观测到音叉共振频率随磁场增强而移向高频端，共振频谱宽度则随感生磁场增强逐步变窄；对应的时域测量分析表明，共振弛豫时间随之逐渐延长. 对于所用的音叉共振体系，尽管共振谱宽与弛豫时间不成反比关系，但是谱宽与弛豫时间倒数近似为线性，且在实验范围内满足Δf·τ<1. 尽管共振频域实验测量与时域DFT分析结果存在差异，但频谱峰中心频率和频宽(半高全宽)等物理参量是一致的. 上述结果说明，若共振弛豫时间较长，意味着激发态能级宽度比较窄；反之，则是激发态能级宽度比较宽. 上述结论适用于分析连续波(核)磁共振过程. 由于调制磁场(扫场)强度随时间变化，从而观测所得磁共振信号既是时域信号，同时也包含着对磁场变化的响应信息. 在近代物理实验课中，微波电子自旋共振(固体)样品的激发态能级宽度较宽而弛豫时间很短，实验测量主要体现磁共振信号随外磁场强度变化情况. 连续波核磁共振(液体)样品的激发态能级宽度很窄而弛豫时间较长，实验测量突出反映共振弛豫过程的尾波信号[1].