第50届国际物理奥林匹克竞赛实验试题2介绍与解答

郭旭波,蒋 硕,安 宇,阮 东,张留碗

(清华大学 物理系，北京 100084)

第50届国际物理奥林匹克竞赛于2019年7月7日至15日在以色列特拉维夫举行. 由清华大学率领代表中国参赛的5名中学生全部获得了金牌，实验和理论总成绩排名分别为第1、第2、第4、第8和第13名，并取得了团体第一、个人总分第一、个人理论第一、个人实验第一的优异成绩[1]. 本届竞赛共2个实验题目[2]. 实验1是光学测量，内容为测量透明圆盘的折射率、衍射光栅的参量和三棱镜的折射率. 实验2是维德曼-夫兰兹定律，内容为测量紫铜、黄铜和铝3种金属的热导率和电导率，以及紫铜的比热容，并验证它们之间的普适关系. 由于篇幅限制，本文将对实验2的试题和解答进行详细介绍.

1 试题介绍

在金属中，热传导主要依靠自由电子的迁移. 因此，热导率和电导率是相关的. 这一规律被称为维德曼-夫兰兹定律. 本实验以合理的高精度测量3种金属的热学和电学参量，包括紫铜、黄铜、铝的电导率和热导率，以及紫铜的比热容，并验证这些参量之间的关系.

实验器材如图1所示，各器材如下：

1为紫铜中空圆管，长为200.0 mm，内直径为6.0 mm，外直径为20.0 mm.

2为黄铜中空圆管，长为200.0 mm，内直径为6.0 mm，外直径为19.0 mm.

3为铝中空圆管，长为200.0 mm，内直径为6.0 mm，外直径为20.0 mm.

4为质量为1.2 g的小磁铁.

5为储水器，为一种以色列当地的锅，锅盖内有散热器，盖顶有螺钉. 提供4 L纯净水，用于倒入储水器.

6为杆#1，见图2(a)，数据单位为mm，精度为0.1 mm. 直径为20.0 mm的紫铜杆.

7为杆#2，见图2(b)，数据单位为mm，精度为0.1 mm. 直径为20.0 mm的复合杆.

杆#1和杆#2均带着多个温度传感器(已连接到测试插口)和接有红色导线的加热器，红色导线用于连接直流电源(第15项装置). 杆外包着黑色绝热海绵.

图1 实验器材

(a)杆#1

(b)杆#2

注意：不要将杆#1和杆#2浸没在水中.

8为绝热盖.

9为数显表的12 V直流电源.

10为数显表，如图3所示，可显示8个温度传感器的读数，还可以显示时间以及用作秒表.

A.12 V直流电源线 B.红色多功能按钮 C.温度传感器测试线 1～8.8个温度读数(单位为℃)

11为测试线，用于将杆上的温度传感器的测试插口与数显表连接起来.

12为电压表，功能应设置为20 V直流电压，如图4所示.

13为电流表，功能应设置为10 A直流电流，如图4所示.

14为导线.

15为加热器的9 V直流电源.

数显表使用说明：用12 V直流电源为其供电. 数显表有2种工作模式：秒表和温度显示. 当用测试线将其与温度传感器连接时，将自动转换到温度显示模式. 当断开测试线时，自动转换到秒表模式且屏幕显示“Timer mode”. 在温度模式下按住红色按钮3 s可重置时间；短暂按下红色按钮可使示值暂停(此时秒表仍在计时)；再次按下红色按钮可恢复温度和时间的实时显示. 在秒表模式下按下红色按钮开始计时，再按一次停止计时，长按可将秒表置零. 数显表连接到每根杆时必须先校准. 这是因为杠上的各个温度传感器并不完全相同，通过校准使得热平衡时杆的所有温度传感器的读数相同. 校准步骤为：首先将温度传感器测试线的一端与杆连接，然后按住红色按钮同时将测试线的另一端连接到数显表. 断开数显表的电源或测试线不会擦除校准结果. 警告：必须先进行校准，然后才能将杆连接到储水器或将其上的加热器连接到电源，以保证校准时杆上的温度是一致的. 在实验过程中如果数显表出现异常，断开其电源再重新连接. 数显表会记录之前的校准结果.

1.实验中使用的10 A挡的位置 2.电流挡的插孔 3.实验中使用的20 V挡的位置 4.电压挡的插孔

1.1 实验A：紫铜、铝和黄铜的电导率(1.5分)

当1块永磁铁在空心导体圆管内下落时，会受到圆管上感应出的涡流的阻力. 因此，磁铁会达到终极速度. 对于实验中的圆管，终极速度为

(1)

(2)

其中，L0=0.2 m是圆管的长度，并且假设磁铁释放后立即到达终极速度.

计算所需的圆管和磁铁的参量为：μ0M=0.65 T，wAl=wCu=7.0×10-3m，wBrass=6.5×10-3m，m=1.2×10-3kg，rm=3.0×10-3m，g=9.8 m/s2.

A.1(1.0分) 使用数显表的秒表模式，测量磁铁穿过铝管、紫铜管和黄铜管所需的时间.

A.2(0.5分) 利用(2)式计算3种材料的电导率.

1.2 实验B：紫铜的热导率(3.0分)

将数显表连接到杆#1的温度传感器插头，并对杆#1进行校准. 将4 L水倒入储水器中，将散热器完全浸没，盖上锅盖.

B.1(0.1分) 记下杆#1放在桌上时的初始温度. 断开温度传感器测试线与杆的连接，去掉绝热盖，把杆#1拧到锅盖上. 注意不要施加太大的力矩. 将测试线重新连接到杆上，如图5所示.

B.2(0.5分) 画出为加热器供电并测试其功率的电路图. 电路图应包括：9 V电源、加热器(已连接到杆上)、电压表、电流表和导线. 导线可作为开关来接通和断开电路.

图5 安装在锅盖上的杆#1

测量热导率的方法是对杆的一端加热，而另一端保持与储水器几乎相同的恒定温度. 在所有温度传感器都近似为稳态时测试.

按照B.2部分的电路图连线，为加热器通电.

B.3(0.1分) 测量并计算提供给加热器的功率P. 通电之后等待15 min. 可以利用这段时间准备后面的实验.

B.4(0.5分) 记录所有8个温度传感器在约15,17.5,20 min时的温度.

B.5(1.0分) 在作图纸上画出3个不同时间的温度传感器的读数与位置的关系. 实验D部分也会用到这幅图.

B.6(0.5分) 利用约17.5 min时的数据，求出紫铜的热导率κ0. 忽略所有的热损耗. 计算17.5 min时杆的平均温度变化率ΔT/Δt.

B.7(0.3分) 与κ的实际值相比，求得的κ0值是高了、低了还是相同？

1.3 实验C：测量紫铜的热损耗和热容量(4.0分)

热容量C由下两式中的任一式定义：

(3)

其中,ΔQ/Δt为对材料的净传热速率，ΔT/Δt为温度变化率. 比热容cp为单位质量的热容量. 紫铜杆的质量为0.58 kg.

关闭加热器电源，断开电路. 拧下杆#1，放在桌子上. 把绝热盖装在杆头. 重新连接加热器电路，并将杆连接到数显表.

注意：在本部分实验中，请勿在未监控温度的情况下使加热器长时间通电.

使杆经历冷却—加热—再冷却的过程，可以得到材料的热损耗和热容量. 加热阶段温度的平均变化应约为2.5 ℃. 冷却—加热—再冷却过程的总时长应为10～15 min，以达到实验所需的精度. 应在实验B部分测量接近稳态时的温度平均值附近做实验.

为了考虑存储在杆中的全部热量，需要跟踪测量其平均温度. 平均温度好的近似是杆的中心位置处的温度.

C.1(1.0分) 进行1次冷却—加热—再冷却过程，记录测量结果，并计算杆的平均温度.

C.2(1.0分) 在作图纸上画出杆的平均温度随时间的变化.

C.3(1.0分) 利用上图计算比热容cp和单位时间的热损耗Ploss(在实验B部分的平均温度附近). 用示意图和公式描述所用方法.

为提高实验B部分得到的热导率的精度，需考虑2种主要机制：透过绝热海绵的径向的热传递导致的热损耗，以及测量时系统并未达到稳态.

作为一级近似，可以假设由于这些机制，沿着杆的单位长度的功率变化ΔP(x)/Δx恒定.

C.4(1.0分) 考虑上述2种机制，写出实验B部分的热导率修正到一级近似的表达式. 利用实验B和C部分的κ0，P，cp，m，Ploss，ΔT/Δt表示修正后的热导率κCu，并计算其数值.

1.4 实验D：黄铜和铝的热导率(1.0分)

将杆#2连接到数显表，并按实验B部分的说明校准杆上的温度传感器(按下红色按钮的同时用测试线将温度传感器连接到数显表).

D.1(0.1分) 将杆放在桌上，记录初始温度.

断开测试线，将杆#2拧在储水器盖上，如图5所示. 重新连接测试线与数显表.

重复实验B部分的步骤，对杆加热使其接近稳态，至少等待15 min再进行测量.

为了达到此部分所需的精度，可以假设杆已达到稳定状态，并且杆上单位长度的热量损失是恒定的.

D.2(0.2分) 记下杆#2上所有8个温度传感器的读数，并计算每一段材料的ΔT/Δx.

与C.4题相同，作为一级近似，假设ΔP(x)/Δx是恒定的.

D.3(0.7分) 写出κBrass和κAl的表达式，并计算其数值.

1.5 实验E：维德曼-夫兰兹定律(0.5分)

E.1(0.5分) 在表格中列出求出的热导率和电导率(κ，σ)，并计算每种材料的L值. 计算时假设在一级近似下热导率不依赖于温度.

2 试题解答

2.1 实验A：紫铜、铝和黄铜的电导率

测得磁铁穿过紫铜管、铝管和黄铜管的时间见表1.

表1 测得的磁铁穿过金属管的时间

计算得到紫铜、铝和黄铜的电导率分别为5.97×107，2.98×107，1.60×107Ω-1·m-1.

2.2 实验B：紫铜的热导率

杆#1放在桌上时的初始温度为22.76 ℃.

为加器供电并测量功率的电路见图6. 加热功率为P=IV=5.51 W.

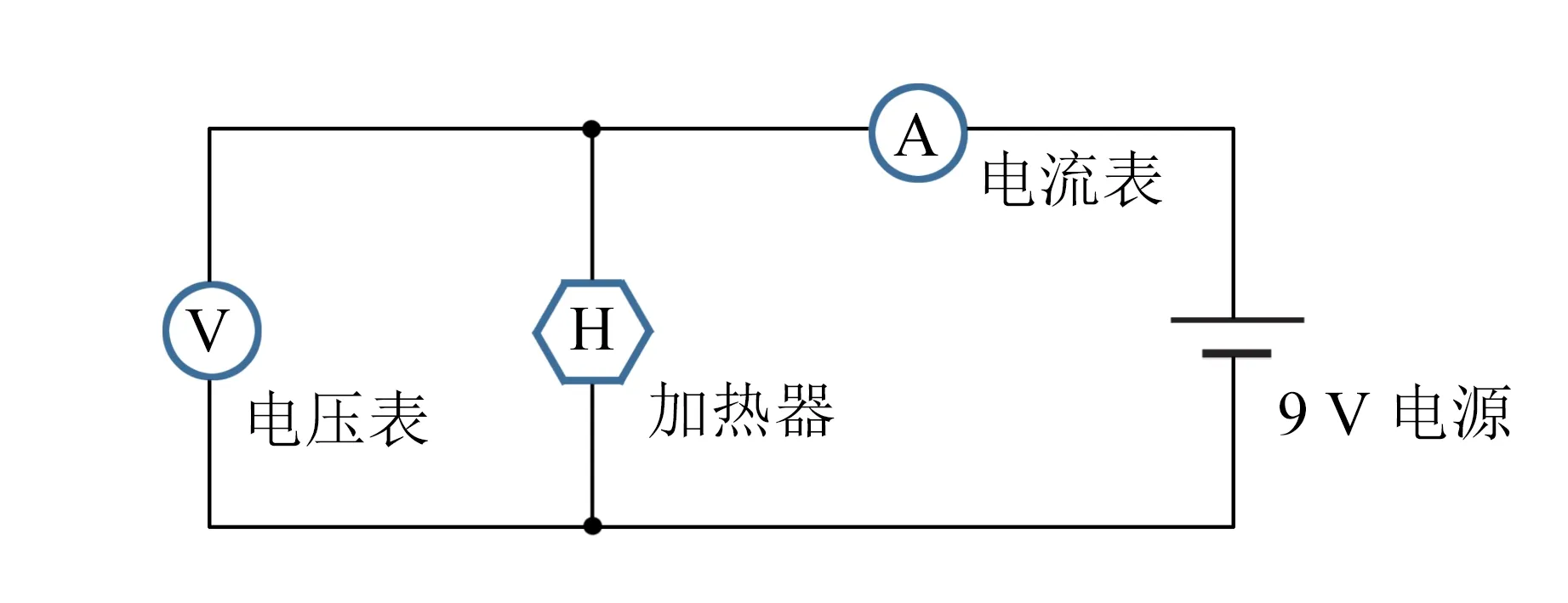
图6 为加热器供电并测量其功率的电路图

加热器通电15 min后，在约15,17.5,20 min时记录的8个温度传感器的读数及其与位置的关系见表2和图7.

表2 不同时间记录的8个温度传感器的读数

图7 不同时间8个温度传感器的读数与位置的关系

紫铜的热导率的计算公式为

420 W/(m·K),

(4)

其中,P为提供给加热器的功率，A为紫铜杆的横截面积，ΔT/Δx为沿紫铜杆长度方向的温度梯度，也就是图7中17.5 min数据的拟合斜率.

17.5 min时紫铜杆的平均温度变化率ΔT/Δt可由图7中杆的中点位置处15～20 min的温度变化求得：

求得的κ0值比κ的实际值高. 这是因为加热器的部分功率透过侧面的绝热海绵损耗了，沿着紫铜杆传递的实际热功率小于加热器功率；此外，系统并未达到稳态，ΔT/Δt≠0，因此加热器的一部分功率还用于对紫铜杆加热使其温度升高.

2.3 实验C：测量紫铜的热损耗和热容量

本部分通过使杆#1经历冷却—加热—再冷却的过程，测量紫铜杆的热损耗和考虑一级近似时的热容量. 测得的实验数据、计算得到的杆的平均温度及其与时间的关系见表3和图8. 杆的平均温度是通过测量离杆的中心位置最近的2个温度传感器的温度并计算其平均值得到的. 冷却—加热—再冷却过程的总时长为860 s，平均温度的变化范围为30.18～32.81 ℃，温度改变量为2.63 ℃，符合实验要求(总时长10～15 min，整个过程在实验B中接近稳态时测量的平均温度值30.8 ℃附近，温度改变量应约为2.5 ℃).

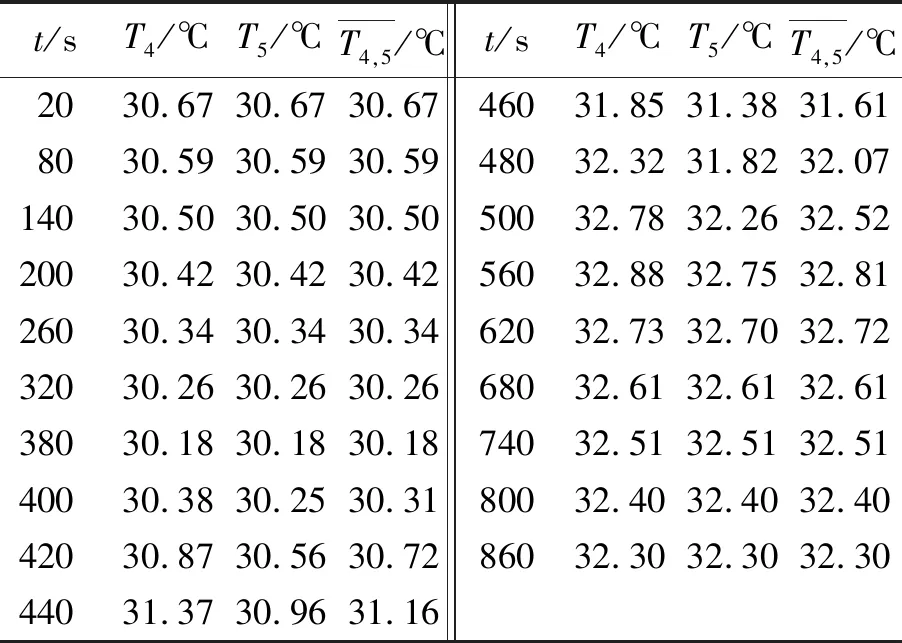
表3 冷却—加热—再冷却过程中杆的温度读数及平均温度

图8 冷却—加热—再冷却过程中杆的平均温度变化

根据本部分实验的测试结果，可以对实验B部分得到的比热容在考虑一级近似的情况下进行修正.

由降温阶段的斜率，得到紫铜杆的热损耗为

(5)

在考虑一级近似的情况下对比热进行修正有2种方法.

方法1使用斜率来计算：

(6)

方法2利用图8中的2条降温曲线在加热阶段的延长线的中点的温度跳变ΔT=2.94 K来计算比热容，可得：

PinΔt=cpmΔT.

(7)

由式(5)和式(7)求比热容cp=386 J/(kg·K)，热损耗Ploss=0.31 W.

杆#1中各个位置处的温度梯度正比于该位置处的热流量. 如图9所示，在杆的始端，热流量等于提供给加热器的功率Pin. 而在杆的末端，由于2种机制引起的热损耗[透过绝热海绵的沿径向的热传递，可由式(5)计算；以及系统未达到稳态，杆的温度仍在升高，可由式(6)第一项计算]从而导致热流量变小.

图9 杆上不同位置处的热流量示意图

作为一级近似，杆上的平均温度梯度正比于杆上的平均热流，可得：

(8)

2.4 实验D：黄铜和铝的热导率

杆#2放在桌上时的初始温度为22.65 ℃. 加器供电1 041 s后各个温度传感器的读数如表4所示. 由各段材料上2个温度传感器的读数及其之间的距离计算得到的相应的温度梯度如表5所示.

表4 加热1 041 s后杆#2上温度传感器的读数 ℃

表5 杆#2上各段材料的温度梯度 K/m

作为一级近似，假设ΔP(x)/Δx是恒定的. 由实验C部分得到的紫铜的热导率，并考虑黄铜段材料的中点位置距离左右2段紫铜段材料中点位置的距离(见图10)，可求得：

同样可得铝的热导率：

图10 杆#2热导率计算示意图

2.5 实验E：维德曼-夫兰兹定律

表6 验证维德曼-夫兰兹定律数据表

3 结束语

本竞赛题的原理和实验方法难度适中,实验任务量较大，我国代表队的学生基本都能完成实验. 在竞赛前的实验培训中特别强调了实验操作、数据记录、数据处理和作图的规范性，避免了学生因为追求实验速度而在细节和过程上丢分. 中国队取得了很好的成绩，1名学生取得了个人实验第1的成绩(15.8分，满分为20分)，另外2名学生的实验成绩(15.0分)接近实验最高分.