基于同态加密的卷积神经网络前向传播方法

谢四江 许世聪 章 乐

1(西安电子科技大学 陕西 西安 710071)2(北京电子科技学院 北京 100070)

0 引 言

随着云技术的不断发展，多种形式的云服务不断涌现。同时，机器学习在人工智能热潮下，受到了诸多研究人员的广泛关注。云服务和机器学习在这种背景下也被巧妙地结合起来，形成了一种机器学习即服务(Machine Learning as a Service, MLaaS)的新型云服务，即机器学习在云资源提供商的基础设施上运行。云机器学习允许在云服务器上训练和部署模型。模型部署后，用户可以使用这些模型进行预测任务。MLaaS适用于医疗、金融、商业等多领域。在医疗领域，它可以为用户提供医疗诊断；在金融领域，它可以为用户分析信贷资料以及在商业领域为用户提供一些商业决策。虽然MLaaS带来了诸多好处，但是也暴露出很严重的问题，即用户数据的安全性和隐私性得不到保障。在一般情况下，机器学习模型训练结束，并进行部署，用户就可以利用模型进行预测任务。然而用户传入的预测样本往往是原始数据，这就会产生潜在的安全和隐私风险。特别是进行医疗诊断预测时，用户传入的是个人隐私医疗数据。这些数据一旦泄露，对用户会造成很多困扰。如何充分利用MLaaS又能比较好地保护用户隐私就成了亟待解决的问题。

同态加密为这一问题提供了解决方案。同态加密最初由Rivest等[1]在保密数据库场景下提出，它作为一种加密数据的方式，在不对密文解密的情况下，也可以对其进行某些操作。Gentry等[2]第一个提出了基于理想格的全同态加密方案，起到了突破性的作用。全同态是指在该方案下允许对加密数据执行任意多次操作。Bos等[3]引入中国剩余定理提出了一种处理大数的同态加密方案，它将密文扩展到几个环元素来分开加密，从而解决了输入数据过大的问题。全同态加密方案具有很好的计算特性，但是也带来了计算缓慢的问题，在实际较大计算任务中暂时还无法使用。现在主要使用微同态加密方案(SomeWhat Homomorphic Encryption, SWHE)来解决实际问题，即限制了一些计算的同态加密方案，如只能进行限定次数的密文乘法。

许多研究人员开始着手解决MLaaS中的安全和隐私问题。其中一个重要方法就是将同态加密和机器学习结合起来。目前许多工作都集中在更简单的模型上，如Graepel等[4]利用层级同态加密方案训练了两个线性二分类模型——线性均值和Fisher线性判别器——保持了训练和测试数据的机密性。Kim等[5]提出了关于加密数据的逻辑回归模型训练方法，使用的加密库是该团队开发的HEAAN，在同态加密的数据集上，获得训练模型需要116分钟，并且取得了较好的准确率和性能。处理Sigmoid函数的方法是使用高阶的泰勒公式。Dowlin等[6]改造一个已经训练好的逻辑回归模型，将用FV同态加密方案加密的个人生物信息数据传入改造模型，得到是否患糖尿病的预测。原始模型激活函数是Sigmoid函数，改造模型将Sigmoid函数处理为在x=0附近展开的7阶泰勒级数，使用的同态加密方案支持库是SEAL，并且对比了给定不同加密参数的用时情况。Cheon等[7]和Giacomelli等[8]也分别提出了隐私保护逻辑回归和隐私保护岭回归方案。在隐私保护下神经网络方面，Dowlin等[9]使用MNIST数据集训练了一个卷积神经网络模型CryptoNets，他们的研究分为训练和预测两个阶段，在训练阶段为9层，预测阶段对网络层进行了整合和去除，分为5层。为了满足同态加密计算特性，激励层使用平方函数，并且使用特殊的加和池化(即滑动窗口中的像素值的加和作为该窗口的结果值)。CryptoNets也借助了SEAL，该库的早期同态加密方案是YASHE， CryptoNets也正是使用的YASHE方案。使用了中国剩余定理处理大数以及批量化处理。在考虑ReLU和Sigmoid非线性函数和同态计算特性的矛盾时，往往采用多项式来替换非线性函数，以保证同态计算特性。CryptoNets作为引入同态加密的隐私保护神经网络方案的领头羊研究，Chabanne等[10]为了扩展到更深层的网络架构，提出了使用多项式逼近激励函数结合批量归一化(Batch Normalization，BN)的处理方法，并分析了层输出稳定性。然而，他们在研究中仅进行了明文实验，虽然分析了乘法深度带来的影响，但是没有给出密文实验的相关结果。Hesamifard等[11]引入了一种新的多项式逼近激励函数方法，结合批量归一化，并在密文上进行了实验，使用的同态加密库是IBM的HELib。还有相关研究关注点在于结合安全多方计算解决隐私保护神经网络问题[12-13]，它们的解决途径包括混淆电路、秘密共享和茫然传输等。

在逻辑回归和神经网络中，最常见的连接方式为全连接方式，这种方式满足同态特性，在同态加密机器学习中尤为常见。然而全连接方式也会产生大量的模型参数，在同态加密情况下，计算变得比较繁杂。本文提出了一种同态加密下的卷积神经网络(Convolutional Neural Network, CNN)前向计算方法，并结合在实数下表现良好的全局平均池化层(Global Average Pooling, GAP)[14]，提出了同态加密下的全局平均池化层，大幅度减少模型参数，从而加快了加密预测的预处理过程。在加密预测方面，该方法用准确率的微小下降换取了预测响应时间的大幅度减少。

1 预备知识

1.1 卷积神经网络

全连接神经网络主要的局限性在于像素比较大的情况下，隐藏层之间会有大量的待训练参数，而且不便于处理高维数据。卷积神经网络的出现解决了参数过多的问题，特别是图像处理方面性能显著。卷积神经网络主要依赖于参数共享，核心是卷积操作和池化操作。在实际使用中，一般经过若干卷积层、激励层、池化层组合，再将特征进行拉伸操作作为全连接层的输入向量，经过全连接层处理后获得输出。经典的LeNet[15]和上述的CryptoNets都是采用这种处理方式。为了便于说明，本文所提到的卷积核和池化窗口的高和宽相等，在高和宽方向上的滑动步长也相等。

(1) 卷积操作。卷积操作是将卷积核和对应输入中的矩阵数据逐个对应相乘，再加和。卷积操作中还有三个重要的单元(卷积核大小、步长和卷积核个数)以及两种补零(padding)方式，即同卷积方式(SAME)和窄卷积方式(VALID)。

卷积核大小一般包括三个维度C×F×F，C表示卷积核对应输入的通道数，F表示卷积核的高和宽。

步长一般包括两个维度S×S，S表示在高和宽方向上卷积核的滑动距离。

卷积核个数一般仅包括一个维度N，N决定了输入经过该卷积层后，输出的通道数大小。

补零方式决定了输出的高和宽的大小。VALID不需要在输入图像周围进行补零，输出的高和宽与卷积核有关系。SAME在计算前需要在输入图像周围进行补零，输出的高和宽与卷积核没有关系。两种方式输出的高和宽对应公式及相应补零规则分别如下：

(1)

式中：I表示输入图像的高(宽)，O表示输出图像的高(宽)，F表示卷积核的高(宽)，S表示步长，·表示向上取整函数。

(2)

式中：I表示输入图像的高(宽)，O表示输出图像的高(宽)，F表示卷积核的高(宽)，S表示步长，P表示输入图像高(宽)需要补零的行(列)数，Pt、Pb、Pl、Pr分别表示上下左右需要补零的具体行(列)数，表示向上取整函数，max{·,·}表示取最大值函数，[·]表示取整函数。

(2) 池化操作。池化操作一般是两种方式，即最大值池化和平均值池化。二者区别在于对池化窗口中值的处理方式。池化操作中具有两个重要的参数(池化窗口大小，步长)以及两种补零(padding)方式，基本性质相同于卷积操作。最大值池化即对池化窗口中的值取最大值，平均值池化即对池化窗口中的值取平均值。

1.2 同态加密

对数据进行加密是保护数据安全和隐私的有效途径。一般的加密方案关注的是数据存储安全，只能对加密结果进行存储和传输，但是不能对其进行运算操作。而同态加密主要关注的是数据处理安全，它可以对加密数据进行运算操作的加密方案。

同态相关数学定义如下：

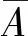
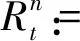
(3)

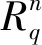
(4)

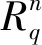
(5)

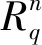
(6)

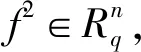
2 同态加密下CNN前向传播计算方法

2.1 同态加密图像预测示意图

同态加密下CNN前向传播计算主要是为了使同态加密下的图像能够通过前向传播计算而得到加密的预测结果。加密预测示意图如图1所示。

图1 加密预测示意图

2.2 预处理

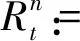
2.3 计算方法

(1) 卷积层。加密域下卷积层输入图像是密文图像，卷积核对应的权重是预处理编码后的明文。卷积层输出大小同样依赖于VALID和SAME方式，高和宽计算方法也同实数网络对应的卷积层相同。输出通道数根据卷积核的个数。下式描述了卷积核作用在输入图像对应的一个密文输出：

(7)

式中：outputD表示卷积核作用区域D的输出，对应输出图像的一个密文像素点，P[wi]表示卷积核作用区域上i的权重明文编码，Epk[vi]表示输入图像对应卷积核上i的像素点密文值，vi表示图像像素点的明文值，这里只是为了形象表示，不需要考虑vi具体是多少，仅仅关注密文本身即可，⊗表示密文和明文乘法，∑·表示密文加法。

(2) 池化层。通常情况下池化层一般是最大值池化层和平均值池化层，然而也存在特殊池化层，如CryptoNets中的加和池化层。在加密域情况下，对于每个池化窗口中的像素值都是密文。令D为池化窗口区域，区域内有n个像素点，Epk[vi]表示窗口中的像素值的密文，outputD记作该区域的输出值。

加密域下最大值池化层方案不可行，事实上：

(8)

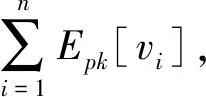
为了保持卷积神经网络的普遍性，加密域下池化操作选择常用的平均值池化，数学描述为：

(9)

式中：数值1/n不能直接与密文和直接相乘；需要通过编码成明文后才能进行乘法操作，P[·]表示对· 进行编码操作，⊗表示密文和明文乘法，∑·表示密文加法。式(9)表明平均池化满足同态计算特性，运算仅包括密文加法与密文和明文乘法。

(3) 激励层。激励层一般使用ReLU、Sigmoid和Tanh作为激励函数，然而这些函数不满足同态特性。为了保证密文域下数据流的正常运算，需要对这些激励函数进行改进。处理方法可以通过函数逼近上述激励函数，使用逼近多项式作为激励函数。CryptoNets在训练阶段就没有选择上述三种常见的激励函数，而使用了平方函数。为了便于和CryptoNets比较计算时延，激励函数也选择平方函数。

(4) 全局平均池化层。本文方法不再使用全连接层接在卷积层、激励层和池化层的组合之后，而是使用全局平均池化层作为全连接层的替代。全局平均池化层计算方法和池化层相同。全局平均池化层的思想在于最后获得的若干通道的数据均值对应分类输出向量。使用全局平均池化层可以大幅度减少模型的训练参数，并且获得较好地准确率。

3 网络结构

3.1 训练阶段

训练阶段网络层分为9层，神经网络示意图如图2所示。

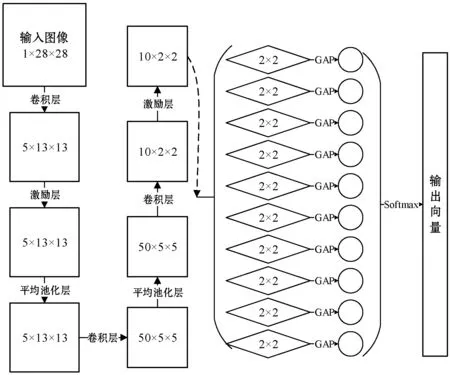
图2 训练阶段神经网络结构示意图

(1) 卷积层——卷积核大小为1×5×5，步长为2，卷积核个数为5，VALID方式，输入大小为1×28×28，输出大小为5×13×13。

(2) 激励层——使用平方函数。

(3) 平均池化层——池化窗口大小为3×3，步长为2，SAME方式，输入大小为5×13×13，输出大小为5×13×13。

(4) 卷积层——卷积核大小为5×5×5，步长为2，卷积核个数为50，VALID方式，输入大小为5×13×13，输出大小为50×5×5。

(5) 平均池化层——池化窗口大小为3×3，步长为2，SAME方式，输入大小为50×5×5，输出大小为50×5×5。

(6) 卷积层——卷积核大小为50×3×3，步长为2，卷积核个数为10，VALID方式，输入大小为50×5×5，输出大小为10×2×2。

(7) 激励层——使用平方函数。

(8) 全局平均池化层(GAP)——每个通道大小为2×2，每个通道的全局平均值作为该通道的输出值。输入大小为10×2×2，输出大小为10×1。

(9) Softmax层——该层主要便于误差的反向传播。

3.2 预测阶段

CryptoNets将激励层作为分割层，并去除了不影响加密预测结果的最后一层，预测阶段CryptoNets重新分为5层。为了便于分析与比较，也将预测阶段将网络分为5个部分：

(1) 卷积层，记为Ⅰ——同训练阶段第1层。

(2) 激励层，记为Ⅱ——同训练阶段第2层。

(3) 线性层，记为Ⅲ——同训练阶段第3～6层。

(4) 激励层，记为Ⅳ——同训练阶段第7层。

(5) GAP层，记为Ⅴ——同训练阶段第8层。

训练阶段第9层Softmax层是单调递增的，不会改变输出向量最大值索引，在预测阶段不再考虑。

4 实验结果与分析

4.1 实验数据

实验数据为MNIST数据集，包括70 000幅手写数字图片，每幅图片为28×28像素，每个像素点值范围[0, 255]。其中55 000幅是训练样本，5 000幅是验证样本，剩余10 000幅是测试样本。由该数据集获得模型参数。

预测阶段的同态加密下的前向传播需要利用这些经过编码处理后的模型参数。预测阶段的输入是对MNIST数据集测试样本的像素点值进行同态加密后的密文图像。

4.2 实验运行环境

实验主要分为两个阶段，模型训练阶段和密文预测阶段。模型训练阶段主要是为了获得模型参数，为密文预测阶段的前向传播提供数据。模型训练阶段使用Python语言借助Tensorflow和Numpy可以高效快速地完成模型的训练和测试，并保存模型参数。在密文预测阶段，选择C++语言，SEAL库在同态加密运算上提供支持，运行时间的统计依赖于Chrono库。具体的环境说明如表1所示。

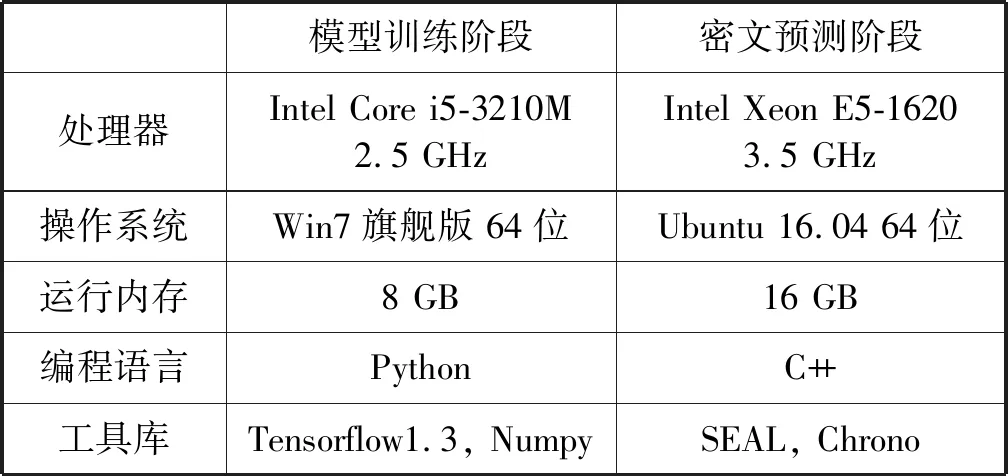
表1 实验运行环境

4.3 实验结果

(1) 准确率。准确率比较如表2所示。

表2 准确率比较

本文利用GAP替换全连接层的方法，在准确率方面略微低于CryptoNets。

(2) 预测时间。由于同态加密中加密参数不同会对预测时间有影像，特别选取了两组加密参数测量时间。

第一组：n=8 192,t1=1 099 511 922 689,t2=1 099 512 004 609,q=2383-233+1。

这里t1·t2>280，q<2384，则密文多项式对应的每个系数需要48 bytes。n=8 192，该预测网络可以接受的批量大小也为8 192，则计时是以一批大小为8 192的测试数据作为基准的。如表3所示，第一组参数下，本文方法对应各层的加密预测时间合计472.8 s，而CryptoNets加密预测时间为570 s，效果对比如表4所示。

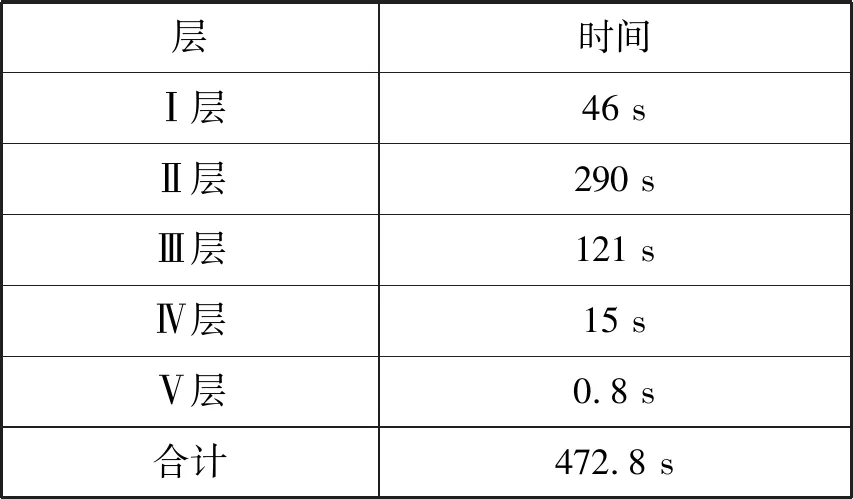
表3 第一组加密参数下本文方法各层运行时间

表4 第一组参数下预测计算时间对比

第二组：n=4 096，t1=40 961，t2=65 537，t3=114 689，t4=147 457，t5=188 417，q1=2191-2 589 751，q2=2191-491 527，q3=2191-2 232 751，q4=2191-2 309 565，q1=2191-15 131 401。

这里t1·t2·t3·t4·t5>280，q<2192，则密文多项式对应的每个系数需要24 bytes。n=4 096，该预测网络可以接受的批量大小也为4 096，计时是以一批大小为4 096的测试数据作为基准的。如表5所示，第二组参数下，本文方法各层的加密预测时间合计189.38 s，而CryptoNets加密预测时间为249.6 s，效果对比如表6所示。

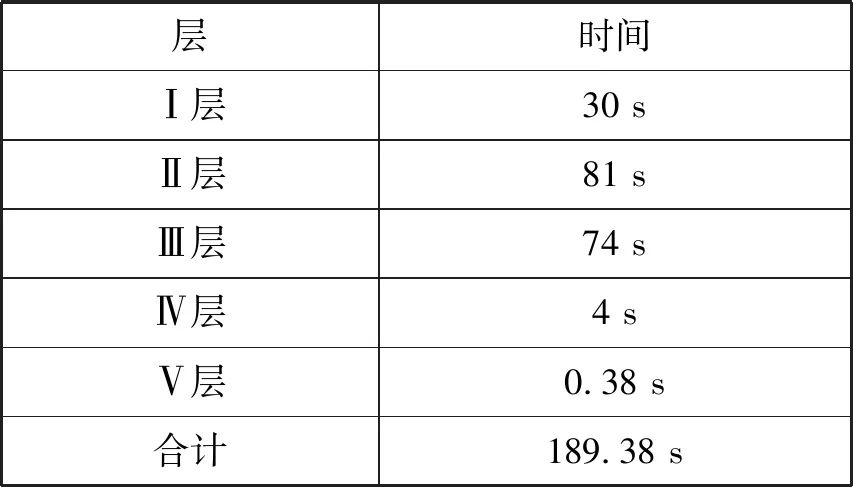
表5 第二组加密参数下本文方法对应各层运行时间

表6 第二组参数下预测计算时间对比

(3) 模型参数分析。在CryptoNets中，第一个全连接层待训练参数个数为100×1 250=125 000，第二个全连接层待训练参数个数为10×100=1 000，合计训练参数个数为126 000。而使用GAP后仅需要待训练参数个数为50×3×3×10=4 500，大大减少了模型参数，简化了参数预处理编码。在同态计算过程中，除了密文和密文乘法外，较为花费时间的是密文和明文乘法。CryptoNets中需要126 000次密文和明文相乘，而使用GAP后仅需要18 000次。

4.4 实验分析

在分类准确率下降较小的情况下，使用GAP可以较好地解决全连接层计算缓慢的问题，在响应时间上获得了较好的提升。GAP大大减少了模型参数数量，简化了对模型参数的处理。

5 结 语

本文将同态加密和卷积神经网络中全局平均池化相结合，提出了加密域下全局平均池化层的前向传播方法。该方法可以在降低较少分类准确率的前提下，大幅度减少加密域下全连接层带来的计算时延，同时减少相关参数数量及服务器预处理参数编码的时间。接下来的研究方向是增强方法的鲁棒性以应对更加复杂的神经网络以及加密待处理数据。