基于正则线性模型的马尔科夫边学习算法

严 曙 胡晓波 王儒敬

1(中国科学院合肥智能机械研究所 安徽 合肥 230031)2(中国科学技术大学 安徽 合肥 230026)

0 引 言

从观察数据集中发现变量之间的因果关系是所有学科的基础，如计算机科学、医学、统计学、经济学和社会科学等[1-4]，并且这个因果关系已被广泛接受用于替代随机对照实验的最佳方案[5-7]。原因是在大多数情况下，获取观察数据的实验可能成本过高、不道德或是不可能的[8-10]。贝叶斯网络作为一种有向无环图模型[4]，可以有效地表示图中所有变量间的因果关系。具体而言，对于网络中目标节点T，该节点仅与其父子节点和配偶节点相关，而与其他节点无关。父子节点和配偶节点的集合称为变量T的马尔科夫边(毯)，目标节点仅与马尔科夫边(毯)相关的性质被广泛用于贝叶斯网络结构学习和机器学习领域中的分类和预测。

从贝叶斯网络发现马尔科夫边(毯)是件容易的事，然而，从数据集中构建贝叶斯网络已被学者证明是NP难题[11]。因此，研究人员提出了各种马尔科夫边(毯)的学习算法。据不完全统计，1996年至2013年之间，就有多达17种代表性的算法问世。这些学习算法大致可分为两类[12]：基于约束学习方法和基于评分学习方法。近五年来，又涌现出更多的马尔科夫边(毯)学习算法[13-17]。但主流算法仍是基于约束学习的方法，主要原因是马尔科夫边(毯)的概率和拓扑特征信息有助于定义有效学习的约束条件，但不能帮助建立局部和全局得分之间的关联[12]。

近年来，基于正则线性模型(正则线性模型方法也属于基于约束学习方法)的马尔科夫边(毯)学习方法也开始被相关文献报道。如：文献[18]使用BIC评分机制在构建贝叶斯网络的过程中借助拉索模型提出一种马尔科夫边(毯)的发现方法(L1MB)，文献[19]通过对岭回归模型的修改，提出了一个岭回归模型的变种模型MRRLM，探寻解释变量与响应变量的关系，具有较大的理论意义。

但是，文献[19]提出的MRRLM中引入了解释变量的协方差，在变量共线的情况下导致MRRLM无法求解，一个直觉的想法是：岭回归模型能代替MRRLM用于马尔科夫边发现吗？如果能，则上述问题迎刃而解; 如果不能，有替代的其他正则线性模型或变种模型吗？为回答上述问题，本文为此展开工作，通过实证的方式研究MRRLM与岭回归模型、拉索模型和弹性网络模型的马尔科夫边(毯)发现效率之间的关系，并尝试提出一个经验性模型NVRRLM, 试图探索其在数据集上的适用性规律。实验中结合置换检验方法正则线性模型能显著提高马尔科夫边的发现效率，但也带来运算代价过高的问题。因此，本文仅在低维(维数小于100)数据集上比较不同模型之间的发现性能。

1 相关工作

1.1 马尔科夫边(毯)学习算法

1996年，两位斯坦福大学的学者Koller和Sahami将马尔科夫边(毯)与特征选择结合起来[20]，开创了马尔科夫边(毯)的研究新热潮，之后涌现了大批的马尔科夫边(毯)的学习算法。但是主流学习算法主要集中在基于约束的方法，因此，此类学习方法所占篇幅较大。

基于约束的方法又可细分为二类[15]：基于条件独立设计的算法(I类)和基于拓扑信息设计的算法(Ⅱ类)。基于条件独立设计的算法按照马尔科夫边(毯)的定义直接构建算法，因此，搜索策略简单，时间效率高，但是样本效率不佳。I类算法最早可追溯到K&S算法[20]和GSMB算法[21]，一些学者对GSMB算法进行优化后，随后相继出现了IAMB[22]及其派生算法(如fast_IAMB,k_IAMB,λ_IAMB)[23-25]。但IAMB及其派生算法推导过程基本上继承了GSMB算法增长、裁剪两阶段框架，难以根本上解决样本低效的问题。基于拓扑信息的设计算法实际上是结合贝叶斯网络的拓扑信息，将推导过程分解成推导父子节点和推导配偶节点两个子过程，其学习效率相对I类较高，但更复杂的启发式规则也带来较高的时间成本问题。Ⅱ类算法典型代表是MMMB和HITON-MB算法[26-27]，随后又出现了改进算法PCMB[24]和IPC-MB[28]，或结合I类的改进算法MBOR[29]算法和DOS算法[30]等。

基于评分的方法实际就是基于打分和搜索的策略。虽然基于评分的方法在贝叶斯网络结构学习中应用非常普遍，但鲜有应用于马尔科夫边(毯)学习的报道。直到2013年才有文献报道马尔科夫边(毯)学习两个算法DMB和RPDMB[31]，据文中实验报告显示RPDMB算法相比PCMB算法有竞争性的准确率，但所需时间成本要多。考虑到IPC-MB的时间效率比PCMB高，可以合理预测IPC-MB算法时间效率远胜于RPDMB算法。即便如此，上述两个算法仍不失一个重要的尝试。

近年来，基于回归模型的马尔科夫边(毯)学习方法也开始有文献报道。相关工作虽不多，但为马尔科夫边(毯)学习方法提供了新的思路。文献[18]使用BIC评分机制在构建贝叶斯网络的过程中借助拉索模型提出一种马尔可夫毯的发现方法(L1MB),但作者并没有进一步给出理论证明。文献[19]通过对岭回归模型进行修改，提出了正则线性模型MRRLM在满足一定条件下寻找解释变量与响应变量的关系，并从理论上回答了模型的非零解所对应的变量就是马尔可夫边(子集)。据其实验结果报道，在基因数据集NOTCH1和RELA上该算法与最新的算法有竞争性的发现效率。

1.2 特征选择与正则线性模型

特征选择又称变量选择，是从特征集中选出最小特征子集(特征变量)满足系统特定度量指标的最优，在机器学习领域常用于提高分类器或回归模型的预测数据的准确性以及数据生产过程的解释能力。特征选择有许多方法，而正则线性模型是其中一种重要的特征选择方法。正则线性模型是在一般线性回归模型的损失函数基础上添加正则化项(或惩罚项)实现的。常见的正则线性模型有岭回归模型和LASSO模型，具体来说，正则化项为L1范数的称为拉索模型(LASSO)，而正则化项为L2范数的称为岭回归模型(RRLM)。通过调整惩罚系数，将参数系数压缩至零或趋向于零，删除掉与其对应的变量，达到变量选择的目的，所以又称系数压缩法[32-33]。在上述两类特征选择方法的基础上，后来相继派生出一系列的算法模型，如群拉索、稀疏拉索和弹性网络等[34-38]。

2 符号约定和背景知识

为了后续工作的展开，需要一些相关概念的定义和定理。本节内容主要来源于文献[19，40]。

2.1 符号约定

本文符号约定如表1所示。

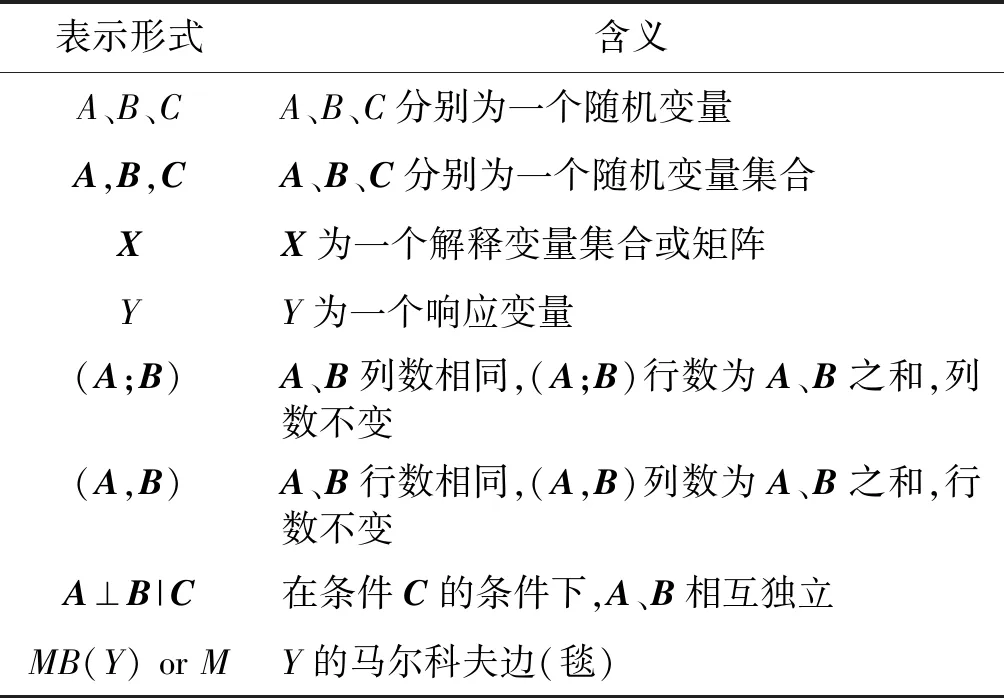
表1 符号表示约定

续表1

2.2 马尔科夫边理论

定义1马尔科夫边(毯)：在随机变量集(Y;X)上，目标变量Y和变量集M⊂X,如果满足Y⊥XM|M,则M称为变量Y的马尔科夫毯，记为MB(Y)；如果对于∀F⊂M,均不满足Y⊥XM|M,，则M称为变量Y的马尔科夫边。

定义2相交属性：联合概率分布为P的变量集X及其任何子集A、B、C和D，如果下式成立：A⊥B|(CD)及A⊥D|(C∪B)⟹A(BD)|C，则称联合概率分布P满足相交属性。

定理1[39]如果变量集X上的联合概率分布P满足相交属性，则对于变量集中任何变量V均存在唯一的马尔科夫边。

定义3全局马尔科夫条件：在有向图G=〈H,E〉中，联合概率分布P满足全局马尔科夫条件当且仅当H中任何不相交的子集A、B和C，如果给定C的情况下，A与Bd-分离，则有A⊥B|C。

定理2[39]有向图G中，如果联合概率分布P满足全局马尔科夫条件，则图中目标节点Y的父节点、子节点及配偶节点构成马尔科夫边(毯)。

2.3 充分降维理论

定义4充分降维：对于条件概率分布为P的变量集(Y;X)，其中Y为一维行变量，X=(X1;X2;…;Xp)。如果存在降维矩阵η∈Rp×d(d≤p)，有Y⊥X|ηTX，则X的空间由p维降为d维。

定义5降维子空间：如果Y⊥X|ηTX成立，则η的列向量构成的子空间，称为Y|X的降维子空间(DRS)，记S(η);如果SY|X是一个降维子空间并且S|Y|X⊆SDRS(SDRS为任意的DRS子空间)，则称子空间S|Y|X是Y|X的中心降维子空间。

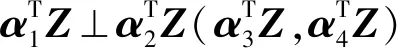
定理3[19]如果变量集(Y;X)的联合概念分布P满足线性相交属性，则存在唯一的中心降维子空间SY|X。

下面介绍马尔可夫边理论与充分降维理论之间的关系。

假设M是联合概率分布P的变量集X的马尔科夫边，PM为M的变量数量，降维矩阵η=(ηM;ηXM),其中，η∈Rp×d(d≤p)，矩阵ηM行数为pM，矩阵ηXM的行数为p-pM。有以下两个定理：

定理4[19]如果变量集(Y;X)满足线性相交属性，则变量集(Y；M)存在中心降维子空间S(ηM),而且S(η)也是变量集(Y;X)的中心降维子空间，其中,ηXM为零矩阵。

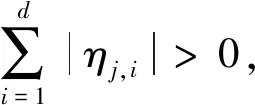
2.4 特征变量与马尔科夫边

特征变量也称预测向量，本节介绍预测向量与马尔科夫边(毯)之间的关系。

定理6[19,40]给定数据集D(样本服从联合分布P)上的变量(Y；X)，一个学习算法L和一个评估学习性能度量M，对于任何变量V⊆X:(1) 如果在预测Y时变量V使性能度量M最大或最小，则V是Y的最优预测向量；(2) 如果不存在V的子集变量满足Y的最优预测向量，则V是Y的最小最优预测向量；(3) 如果V是最小最优的预测向量且基数最小，那么V是Y的最佳预测向量。

性能度量M的例子包括最大似然估计、负均方误差等损失函数。

定理7[19,40]如果条件概率分布P(Y|X)可以准确估计，性能度量M能最优化，并且算法L可以近似任意条件概率分布，则:(1)M是变量Y的一个马尔科夫毯当且仅当M是Y的最优预测向量；(2)M是变量Y的一个马尔可夫边当且仅当M是Y的最小最优预测向量;(3)M是Y的最小基数的马尔可夫边当且仅当M是Y的最佳预测向量。

由定理7可知，如果只存在一个马尔可夫边，如相交属性成立时，马尔可夫边是最小最优的预测向量，反之亦然。如果存在多个马尔可夫边，则马尔可夫边且基数最小是最佳预测向量，反之亦然。

3 变种岭回归模型

本节在介绍变种岭回归模型之前，首先介绍数据集上变量共线与协方差矩阵奇异之间的关系。

3.1 变量共线与协方差矩阵奇异

对于设计矩阵X=(X1,X2,…,Xp),Xi∈Rn，i=1,2,…,p,变量共线即意味着存在不为零的向量k=(k1,k2,…,kp)T和常量C，使下式成立：

k1X1+k2X2+…+kpXp=C或kTX=C

容易得：Var(kTX)=kT∑Xk=Var(C)=0。

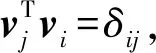
又因为∑X=VDVT，其中，V由协方差的特征向量组成，VVT=E(单位阵)，D是对角线元素为特征值对角阵，因此，当存在变量共线时至少存在一个λi=0，此时协方差矩阵为奇异阵，反之也然。

3.2 变种岭回归模型

线性回归模型：Y=α+βTX+ε，其中：Y∈RK×n,X∈Rp×n,α∈RK×n，β∈Rp×K,ε～N(0,σ2I)。

定义7GJMW条件： (1) 全局马尔科夫条件成立；(2) 联合概率分布(Y;X)满足线性相交属性；(3) 设计矩阵X的协方差矩阵正定;(4) 当Y⊥X|ηTX时，E(X|ηTX)是ηTX的线性函数。

注：GJMW条件命名取四个条件的英文首字母。

3.2.1修改的岭回归模型(MRRLM)

修改的岭回归模型源于文献[19]，该模型实际上是岭回归模型的一个变种。

定理8[19]如果GJMW条件成立，令K为α、β的维数，k∈[1,2,…,K],β为非零矩阵，并且α,β的估计值α*,β*使下式取得最小值:

arg minE{u(α+βTX,Y)}+λtr(βT∑Xβ)

(1)

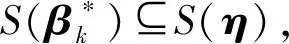
在实际应用中，变量Y通常为一维变量即K=1，此时，对应的α、β也是一维变量。令β为非零向量且β=(∑X)-1/2γ，则式(1)等价于下列岭回归模型：

arg minE{u(α+γTZ,Y)}+λγTγZ=(∑X)-1/2X

(2)

上述定理给出了该模型的解与降维矩阵之间的关系，同时也给出了该模型只能发现马尔科夫边子集的原因。由定理4、定理5、定理7和定理8知：变量Y的马尔科夫边变量子集可以从β矩阵非零(行)系数选出。从式(2)可以看出，协方差矩阵是非奇异的。换句话说，对于变量共线的数据集，该模型理论上无法应用。

3.2.2新变种岭回归模型(NVRRLM)

由上节知，对于变量共线数据集，MRRLM理论上无法处理或实际应用效果不佳，本节提出一种新的变种岭回归模型(NVRRLM)试图解决该问题。

如果GJMW成立，α、β为一维向量，且β≠0，并且α*,β*使下式取得最小值：

arg minE{u(α+βTX,Y)}+λtr(βT(∑X+δ2I)β)

(3)

则有S(β*)⊆S(η)。其中，S(η)是任意降维子空间，u为凸函数，δ为调控参数，λ>0为模型参数。

显然新模型NVRRLM是在MRRLM的基础上修改而得，此时协方差奇异并不影响模型的应用，因此，在满足一定条件下，既可适用共线数据集，也可适用非共线数据集。

3.3 算法及分析

如算法1所示，X和Y为输入数据集，其中X=(X1,X2,…,Xp)，Xi为n维行向量，Y为一维行向量;Ref_mb_num是指参考算法返回的马尔科夫边中的变量数;NumPermute是置换检验中的重复计算数量;crp_mb是算法1返回的结果。算法1的第一行是正常岭回归模型的求解问题，有许多现有的工具和软件可以求解。本文使用Glmnet工具包中的cvglmnet函数并且选择10次交叉验证来选择模型参数λ和估计系数β0；第2行到第9行是使用置换检验[41]的方法计算p值；第10行是将p值从小到大排序得到的X变量的索引序列。第12行返回p值序列中前面Ref_mb_num个变量的索引集crp_mb。根据定理4、定理5、定理7和定理8,crp_mb为马尔科夫边的子集。

算法1正则线性模型马尔科夫边发现的通用算法

INPUT: X,Y,Ref_mb_num,NumPermute

OUTPUT: crp_mb

1: Calculate β0and λ with ridge regression(or LASSO etc)

2: Calculate the number of the column of XT:p;

3: Set the matrix mat_p(p,NumPermute),

4: For k=0 to NumPermute do

5: Random perm Y.

6: Calculate β with ridge regression(or LASSO etc)

7: Calculate mat_p(:k)=(abs(β)≥abs(β0))

8: End for

9: Calculate p_value:(sum(Mat_pT)+1)./(NumPermute+1)

10: Calculate index sequence of p_value_index from small to larger

11: Obtaining crp_mb: p_value_index(1:Ref_mb_num)

12: return crp_mb

在算法1基础上增加了协方差运算和变量变换很容易写出MRRLM的算法实现，具体实现算法如算法2所示。

算法2MRRLM马尔科夫边发现算法

INPUT: X,Y,Ref_mb_num,NumPermute

OUTPUT: crp_mb

1: Calculate covariance matrix: xCov

2: Data transformation: X=xCov-0.5X

3: Calculate γ0and λ with ridge regression

4: Calculate original β0=xCov-0.5γ0.

5: Calculate number of the row ofX: p

6: Set the matrix mat_p(p,NumPermute)

7: For k=0 to NumPermute do

8: Random perm Y

9: Calculate γ with ridge regression

10: Calculate original β=xCov-0.5γ

11: Calculate mat_p(:, k)=(abs(β) ≥abs(β0))

12: End for

13: Calculate p_value=(sum(Mat_pT) + 1)./(NumPermute+1)

14: Calculate index sequence of p_value_index from small to larger

15: Calculate crp_mb: p_value_index(1:Ref_mb_num)16: return crp_mb

新变种岭回归模型(NVRRLM)马尔科夫发现算法与算法2基本上一致，只要按照式(3)修改协方差矩阵就可以了，此处不在赘述。

4 实验模拟与分析

围绕实验目标，考虑置换检验运算成本太高及数据集的代表性，选择数据集维数低于100来源于十个行业的标准数据集，借助工具软件DAGlearn[18]产生10个连续数据集和10个二值离散数据集，数据样本数分别是{300, 600, 900, 1 200, 1 500}，相当于100个数据集。其数据集属性见表2，MB表示马尔可夫边。

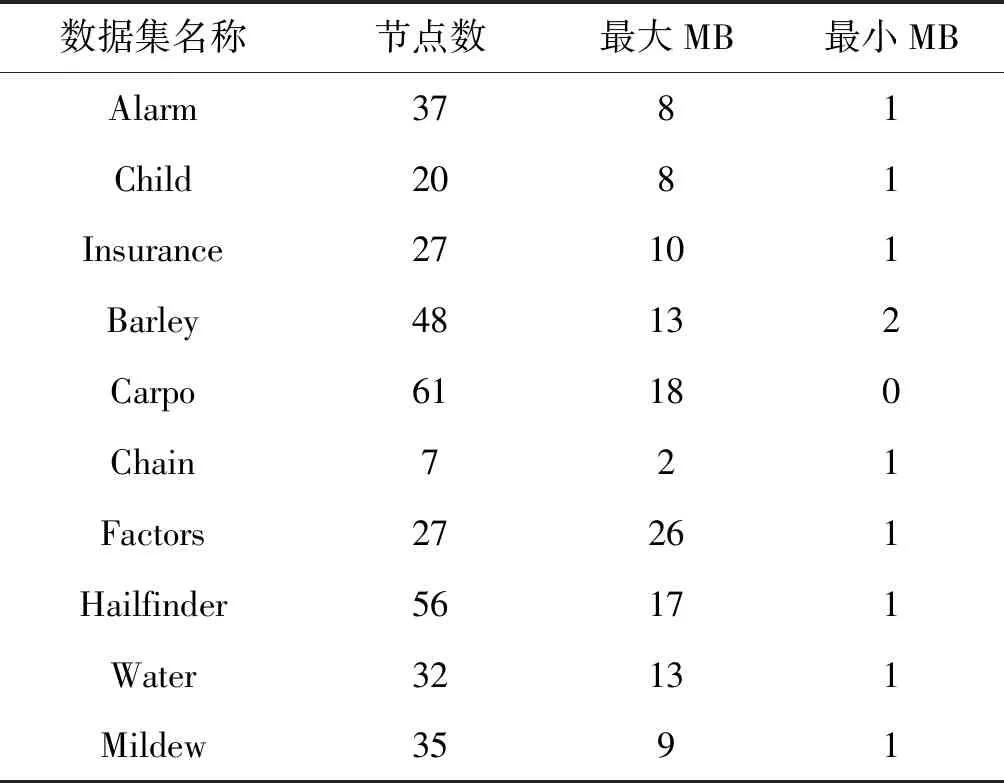
表2 数据集及其属性

4.1 实验设计

从图1和图2可以看出，在连续数据集上IAMB算法整体发现性能和准确率最好，而在二值离散数据集上HITON-MB整体性能和准确率最好，因此，分别选取IAMB和HITON-MB作为正则性线性模型的参照算法。

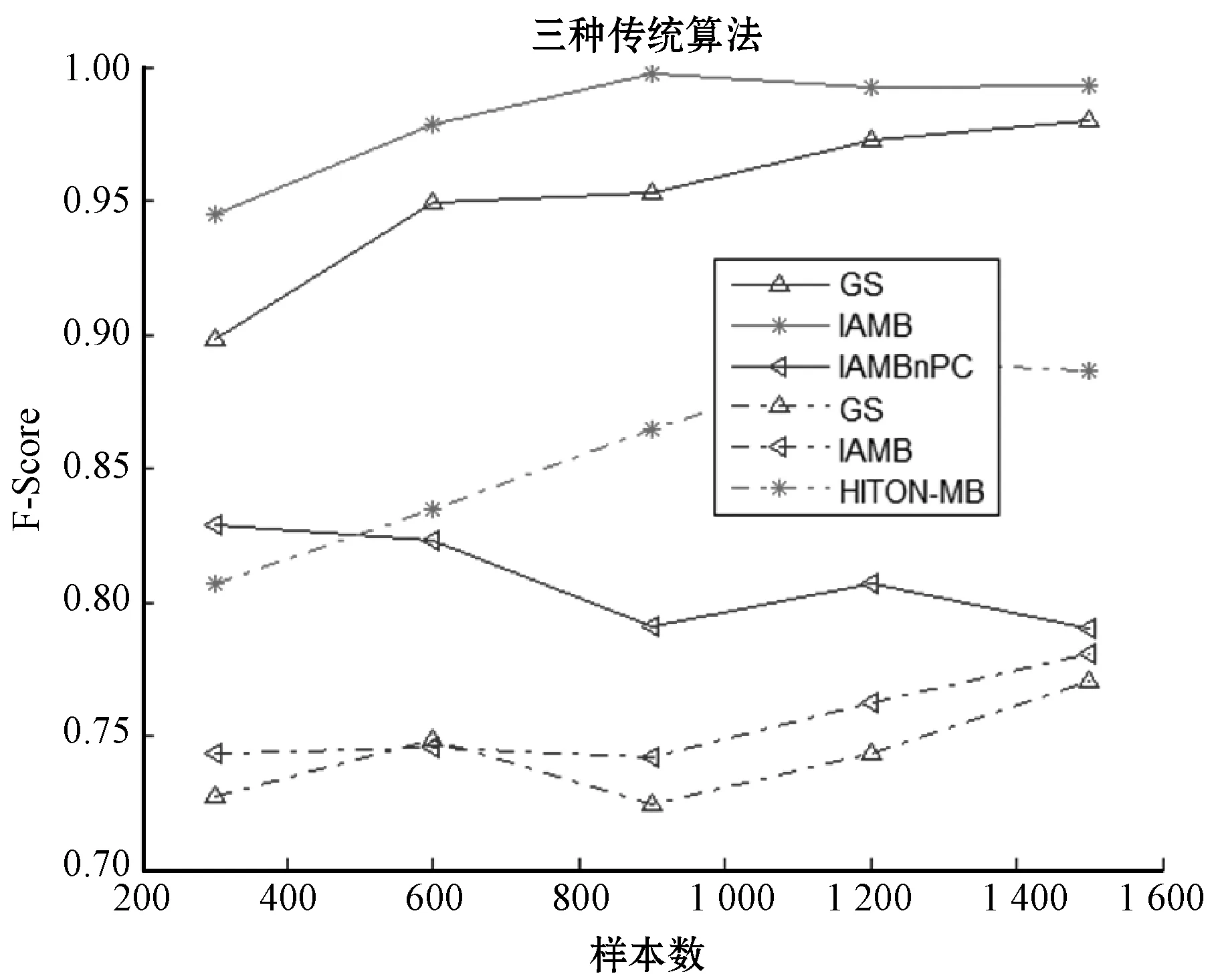
注：实线代表连续数据集，虚线代表二值离散数据集图1 传统算法在数据集上平均F-Score

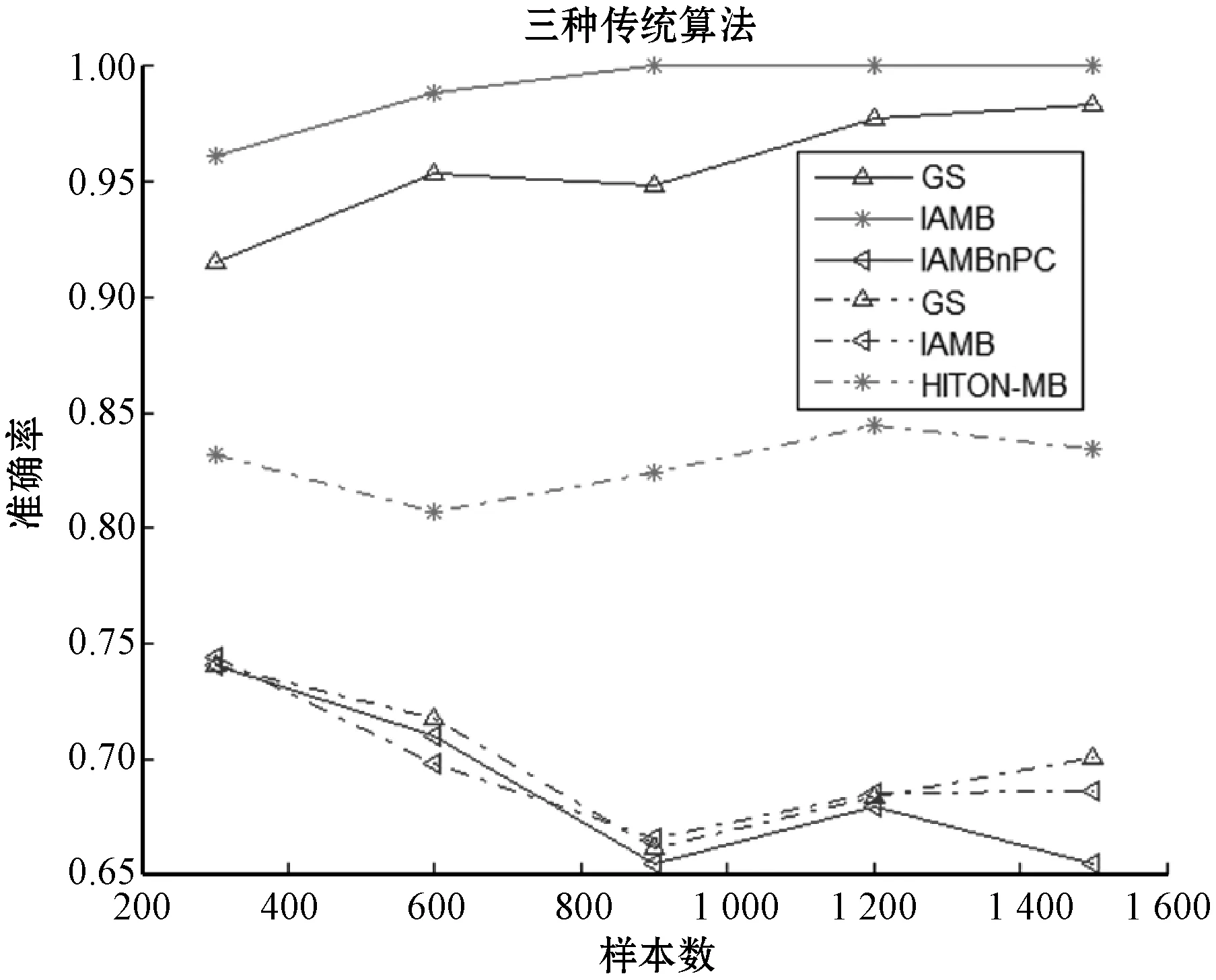
注：实线代表连续数据集，虚线代表二值离散数据集图2 传统算法在数据集上平均准确率

实验设计如下：

(1) 选取合适的模型。依据实验目标，分别选取MRRLM、岭回归模型、拉索模型和弹性网络模型(参数α取值分别为{0.3,0.6,0.8})。

(2) 确定目标变量数。基于运算成本考虑，采取随机抽取若干目标节点的方法来评估数据集的发现效率。本实验采用的规则是：如果数据集变量(维数)数大于15，则随机抽取15个目标节点，否则抽取所有数据集变量作为目标变量。

(3) 确定置换数和模型参数。置换检验方法中，理论上置换数越高，发现效率越准确，但同样带来时间效率的问题，本实验置换数设定为199。同样的原因，在置换检验方法重复计算估计参数时，正则线性模型的模型参数使用首次交叉验证法所得的模型参数。

(4) 生成P值序列。当估计参数T分布存在时，先采用T分布计算P值，再用置换检验方法计算P值，目的是考察两种P值计算方法对于发现效率的影响；当估计参数T分布不存在时，则采用置换检验方法计算P值。

(5) 确定模型评价指标。常用的评价指标有准确率(Precision)、召回率(Recall)以及两者加权调和平均(F-Score)。本实验仅考察模型的准确率、F-Score和运行时间。F-Score计算公式为：F-Score=2×precision×recall/(precision+recall)。

显然，F-Score数值越大，发现效率越好。由于部分数据集上真实马尔可夫边的个数为零，影响相关评价指标的计算，因此，约定如表3所示。

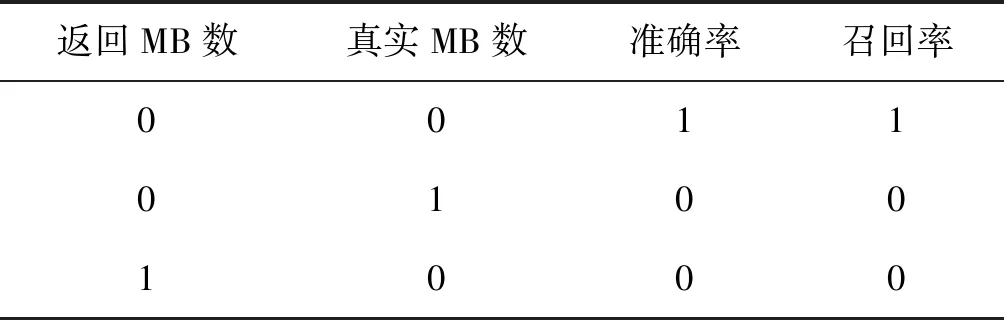
表3 评价指标约定

表3所述的“返回MB数”是模型返回的MB中变量数量，“真实MB数”为数据集上已知真实的MB中变量数量，未知的数据集MB长度可事先估计给定。本实验输出结果还包括运算时间。

完成上述过程，将10个二值离散数据集上的马尔科夫边发现效率汇总平均后，作为低维二值离散数据集上各模型的马尔科夫边发现效率。同样，将10个连续数据集上的马尔科夫边发现效率汇总平均后，作为低维连续数据集上各模型的马尔科夫边发现效率。

4.2 结果分析

4.2.1MRRLM(-P)与RRLM(-P)比较

MRRLM(-P)与RRLM(-P)的比较结果如图3-图5所示。

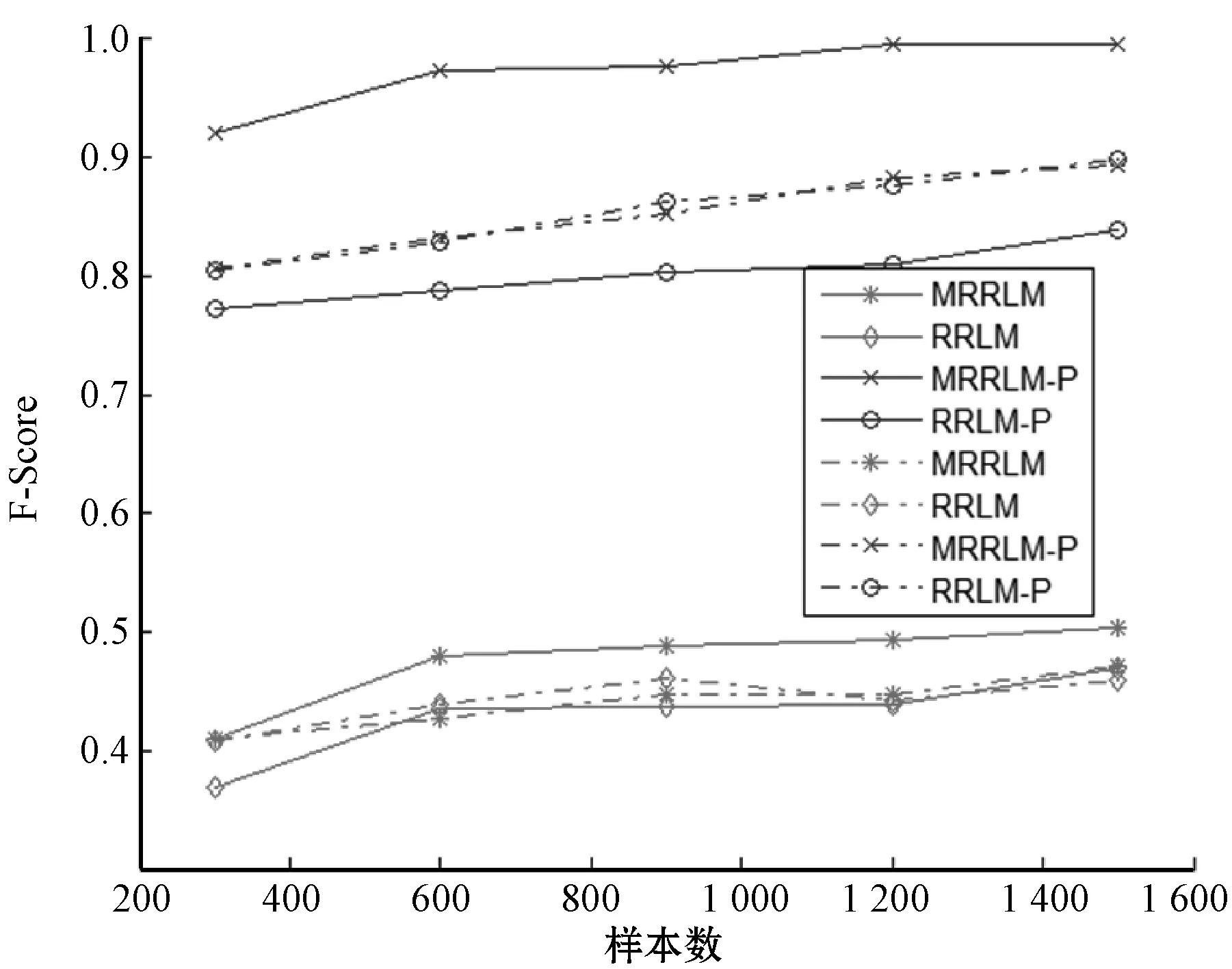
注：实线代表连续数据集，虚线代表二值离散数据集图3 MRRLM(-P)与RRLM(-P)之F-Scroe关系图

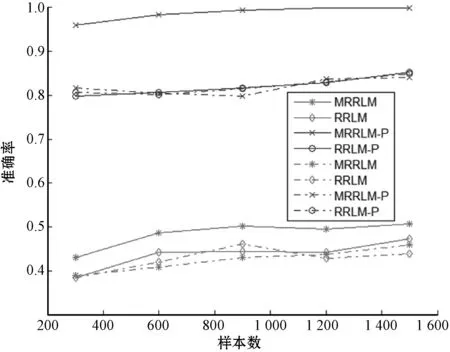
注：实线代表连续数据集，虚线代表二值离散数据集图4 MRRLM(-P)与RRLM(-P)之准确率关系图

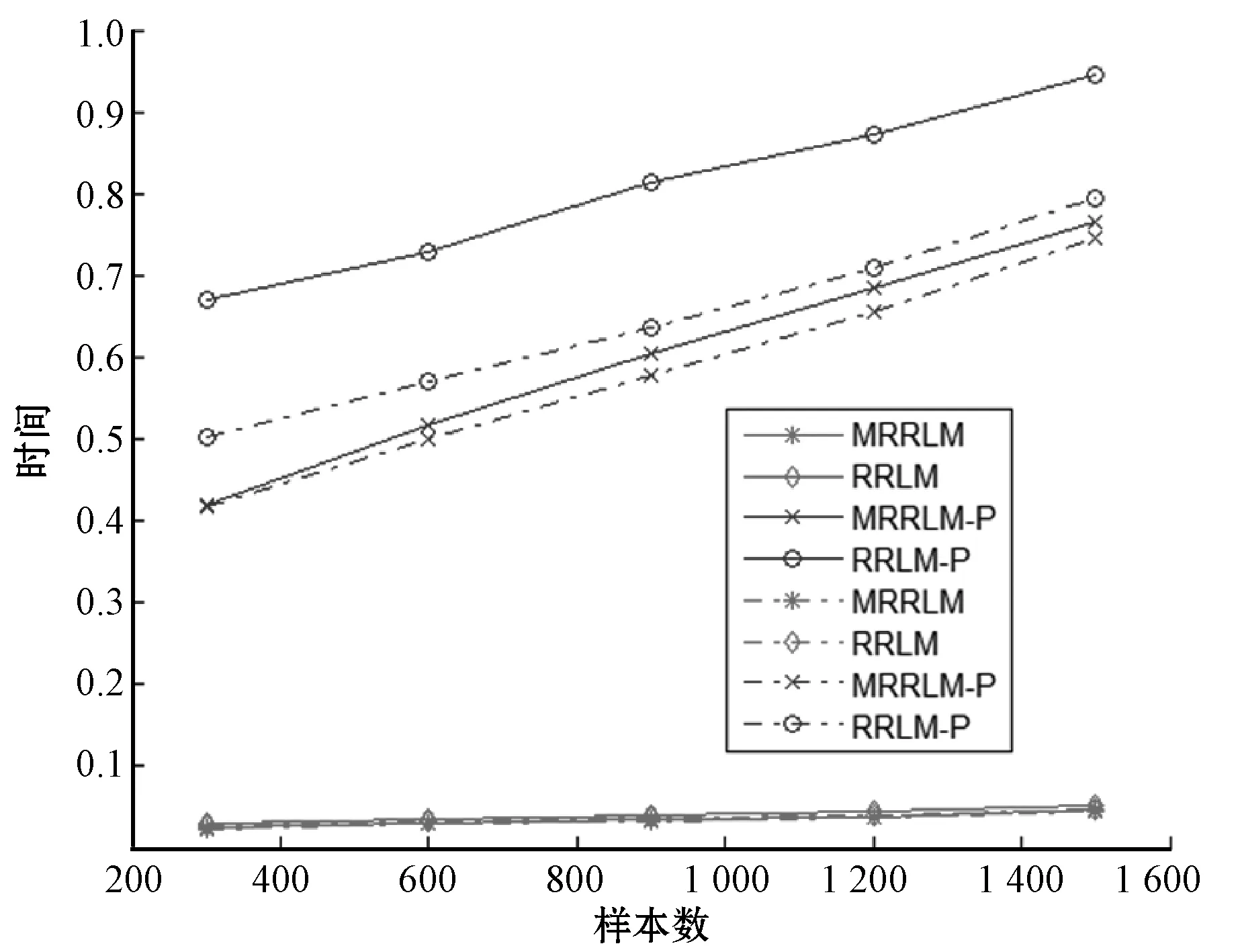
注：实线代表连续数据集，虚线代表二值离散数据集图5 MRRLM(-P)与RRLM(-P)之运行时间关系图

由图3-图5可以看出，在二值离散数据集上，除了运算时间有差别外， 从准确率和总体性能(F-Score)来看，MRRLM(或MRRLM-P)与RRLM (或RRLM-P)马尔科夫边(子集)的发现效率基本相近；而在连续数据集上， MRRLM马尔科夫边(子集)的发现效率则远远高于岭回归模型。从图中还可看出，两种回归模型采用置换检验后，各自的发现效率均有了显著提高。如在连续数据集上，采用T分布方法的MRRLM的F-Score值在0.5以下，而采用置换检验方法的MRRLM-P的F-Score数值快速提升至0.9以上，表明置换检验对模型发现效率有着重要作用。从运算时间来看，MRRLM和RRLM的运算时间均很小并且很相近，结合置换检验后，MRRLM-P和RRLM-P的运算时间明显增加，并且随着样本数的增加运算时间也逐渐增加。

4.2.2正则线性模型与传统算法比较

正则线性模型与传统算法的比较结果如图6-图8所示。

注：实线代表连续数据集，虚线代表二值离散数据集图6 正则化算法与传统算法之F-Score关系图

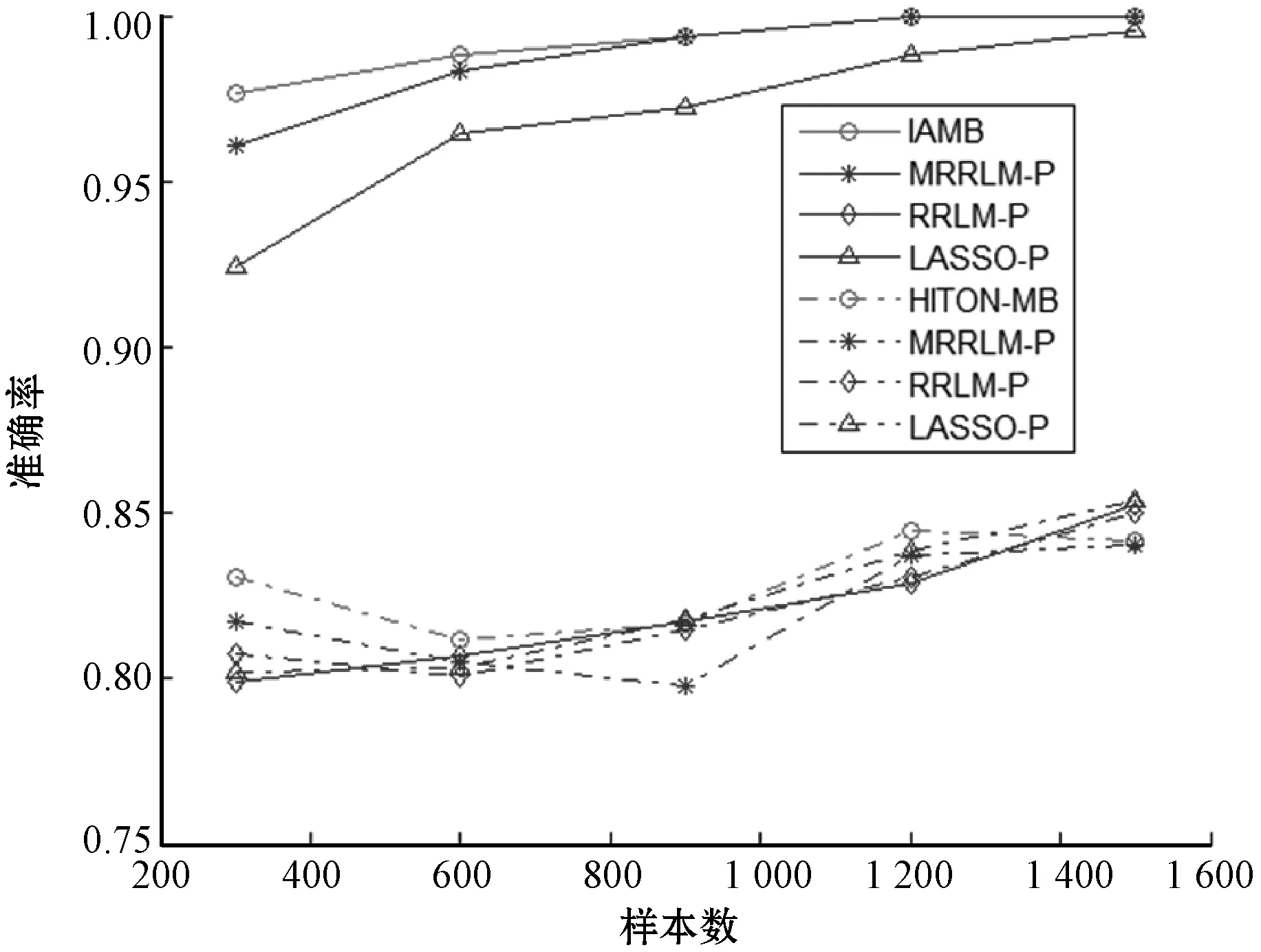
注：实线代表连续数据集，虚线代表二值离散数据集图7 正则化算法与传统算法之准确率关系图

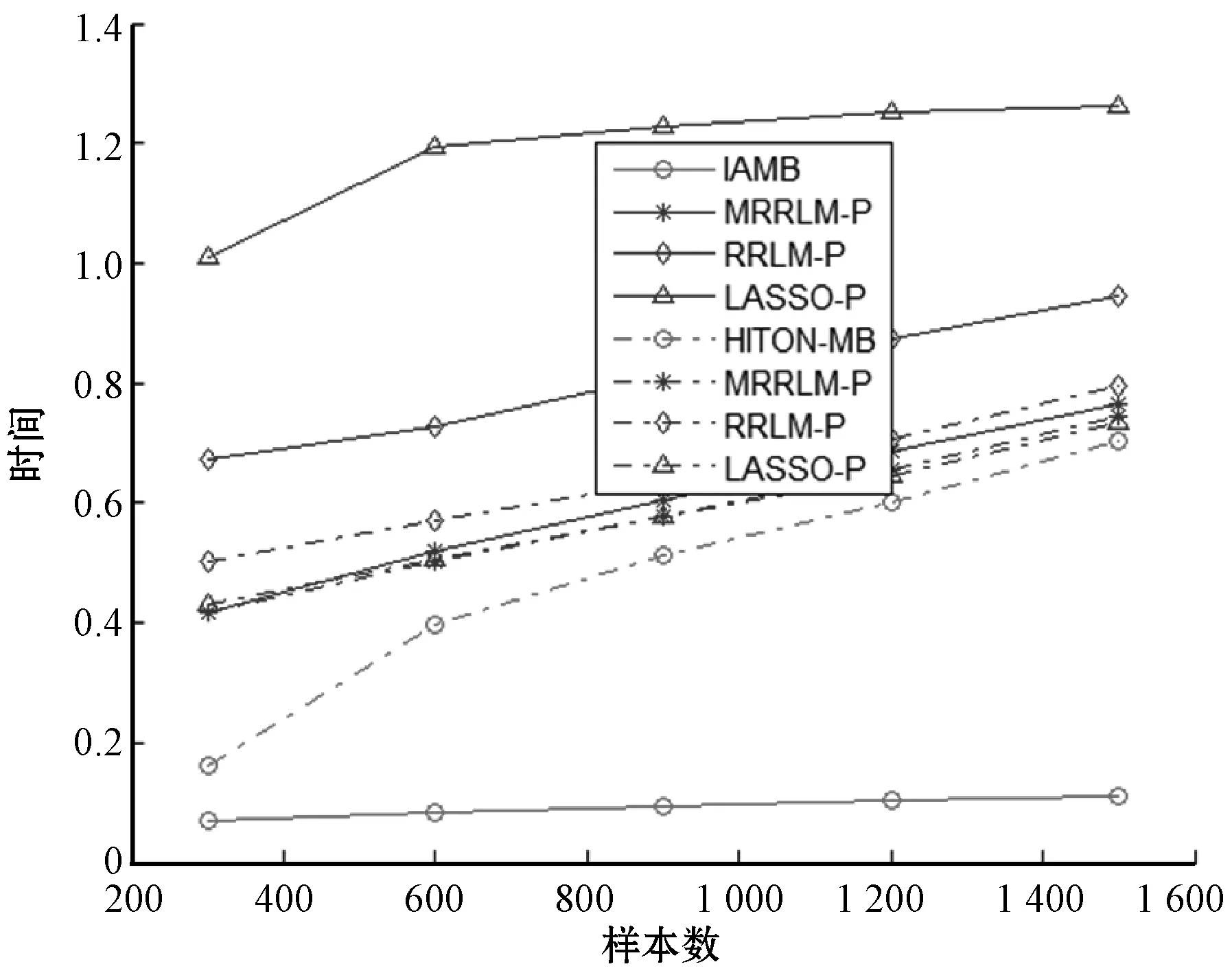
注：实线代表连续数据集，虚线代表二值离散数据集图8 正则化算法与传统算法之运行时间关系图

由于拉索模型估计参数的T分布，因此本次仅局限于结合置换检验的图中所示正则线性模型。由图6-图7可以看出，在连续数据集中传统算法IAMB无论在准确率还是总整性能(F-Score)方面，其马尔科夫边的发现效率均高于正则线性模型。例如在连续数据集上，传统算法IAMB的准确率在97%以上，召回率在95%以上。结合置换检验的MRRLM-P和LASSA-P的准确率在96%以上，召回率在93%以上，均略低于传统算法IAMB的发现效率；而结合置换检验方法RRLM的准确率在80%～85%之间，召回率74%～83%之间，也远低于传统算法IAMB。而在二值离散数据集上，图中所示的几种算法的评价指标基本相近，但HITON算法发现效率略高于正则线性模型。两类数据集上总体发现效率均随着样本数增加而增加。从图8中的运行时间来看，传统算法用时最少，而正则线性模型算法普遍用时过长，并且连续数据集上的运行时普遍高于二值离散数据集。但在低维数据集上正则线性模型的运行时间还在可接受的范围之内。

4.2.3不同参数的弹性网络模型间比较

不同参数的弹性网络模型之间的比较结果如图9-图11所示。

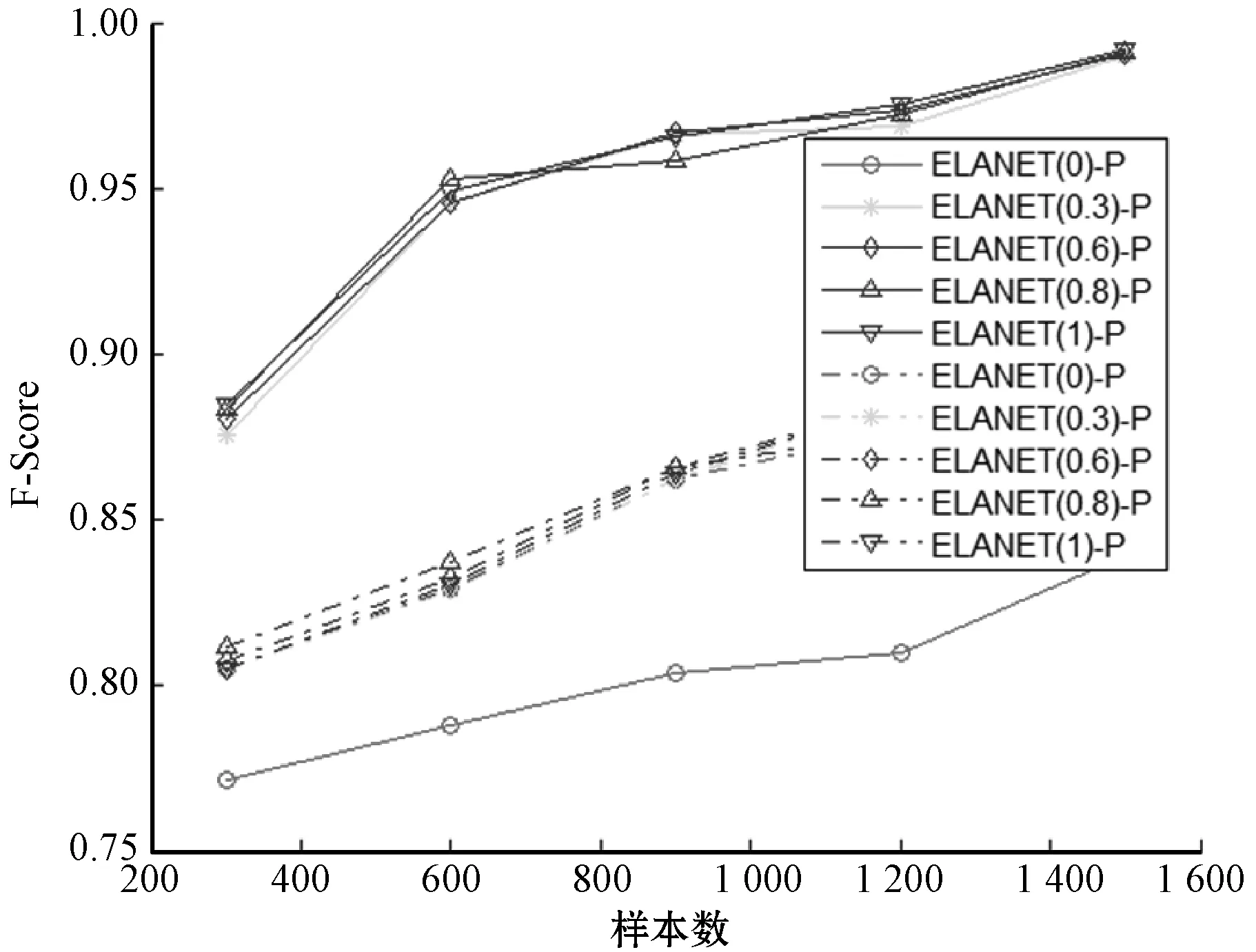
注：实线代表连续数据集，虚线代表二值离散数据集图9 不同参数弹性网络模型之F-Score关系图

注：实线代表连续数据集，虚线代表二值离散数据集图10 不同参数弹性网络模型之准确率关系图

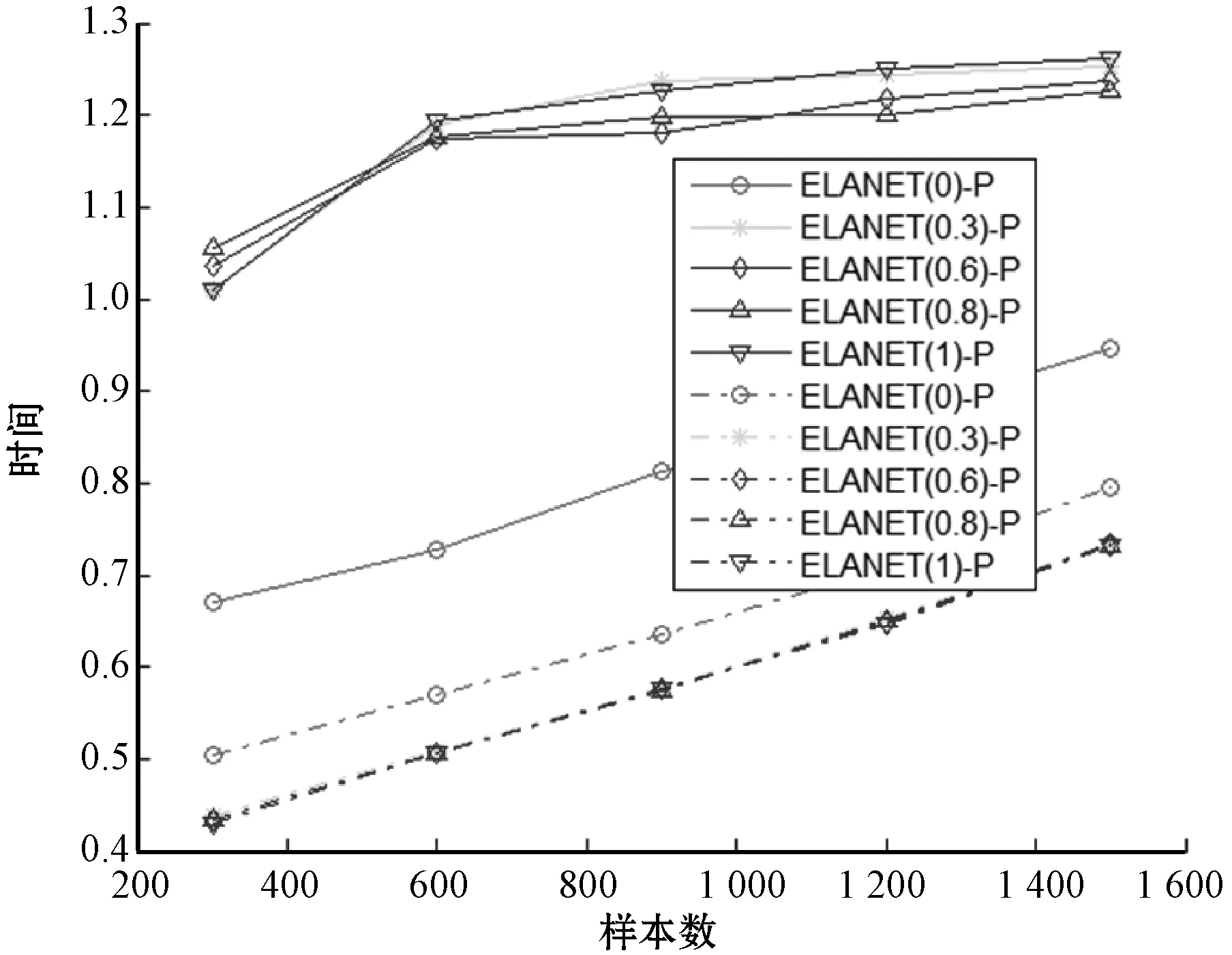
注：实线代表连续数据集，虚线代表二值离散数据集图11 不同参数弹性网络模型之运行时间关系图

由于弹性网络模型(参数等于0除外)不存在T分布，因此，只考察采用置换检验方法的弹性网格模型。由图9、图10可以看出，从准确率和整体性能来说，不同参数{0,0.3,0.6,0.8,1}对应的弹性网络模型在二值离散数据集上形成一束走势基本相同的曲线族，说明弹性网络模型的发现效率基本相近；而在连续数据集上，参数等于0即为岭回归模型时除外，其他弹性网络模型与二值离散数据集上也有类似的结论。从图中还可看出连续数据集上，相同参数的弹性网络模型的总体发现效率高于二值离散数据集上的发现效率，说明连续数据集更适合使用弹性网络模型发现马尔科夫边(毯)。从运算时间上来看，连续数据集上弹性网络模型运算成本比二值离散数据集更高，说明发现效率的提高是以牺牲时间效率为代价的。所有的模型的运算时间整体上均随着样本数的增加而呈逐渐上升，这与人们的认识保持一致。

4.2.4NVRRLM与MRRLM比较

为验证新模型NVRRLM在数据集上的马尔可夫毯的发现能力，选取四个变量共线离散数据集和对照的四个变量非共线离散数据集。数据集对应用数据源文件如表4所示，数据集上模型的评价指标结果如表5所示。

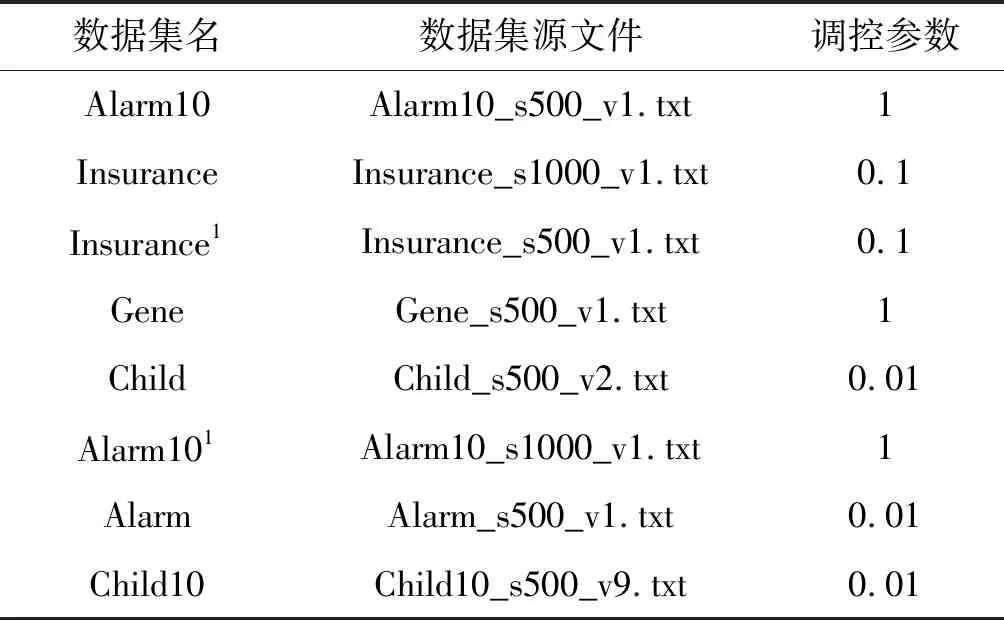
表4 数据源文件名和NVRRLM调控参数

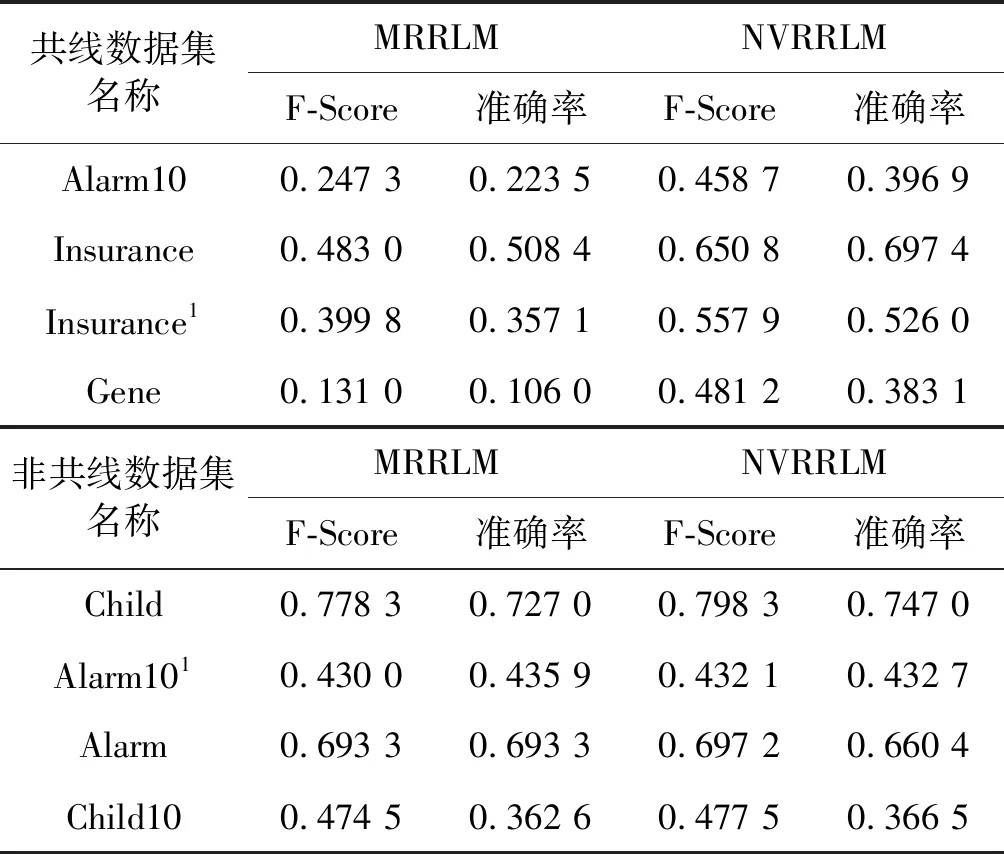
表5 两组数据集上NVRRLM与MRRLM比较

从表5可以看出，虽然理论上MRRLM无法应用变量共线的数据集，但在实际应用时仅是发现效率降低。原因在于数值“0”在计算机数值存储时与定义的小数位多少有关，通常当数值小于10-12时，该数值为零。但此时马尔科夫边的发现效率随着协立差矩阵接近零程度不同而不同程度下降。NVRRLM的发现效率普遍高于MRRLM，而且有些数据集上发现效率提高很明显。如在Gene数据集上，F-Scroe从0.131 0能提高到0.481 2。在变量非共线数据集上，两者模型的发现效率基本相等。因此，作者大胆推测NVRRLM完全可以代替MRRLM用于变量共线数据集上马尔科夫边的发现，同时也可适用于变量非共线数据集。

5 结 语

本文通过实验的方式求证的MRRLM与RRLM的马尔科夫边(毯)发现效率之间的关系，并参照传统算法，考察拉索模型以及弹性网络不同参数模型间的马尔科夫边(毯)的发现效率。实验结果表明：在低维二值离散数据集上，岭回归模型、拉索模型和弹性网络模型与MRRLM有着相近的马尔科夫边(毯)的发现效率，因此，岭回归模型、拉索模型和弹性网络模型完全可以替代MRRLM用于马尔科夫边(毯)发现，解决了MRRLM由于协方差奇异而无法求解问题；而在低维连续数据集上，结合置换检验方法的拉索模型和弹性网络模型(参数为零除外)的发现效率与MRRLM基本相近，并逼近传统算法的发现效率，完全可以替代MRRLM用于马尔科夫边(毯)发现，解决了变量共线数据集求解问题，但结合置换检验方法的RRLM马尔科夫边(毯)发现效率最低，远低于结合置换检验方法的MRRLM。此外，实验结果显示本文新提出的经验模型NVRRLM完全可代替MRRLM适用于变量共线数据集和变量非共线数据集上马尔科夫边(毯)的发现。

结合置换检验统计方法的正则线性模型，虽然解决了解释变量协方差矩阵的奇异问题或者变量共线问题， 但是也存在一些缺陷。首先，置换检验方法适用于分布未知的小样本数据，对大样本或高维数据由于所需时间太长，而失去应用价值；其次，用于发现马尔科夫边的正则线性模型需要事先指定马尔科夫边(毯)期望值，与早期的K&S相似；再次，正则线性模型仅在某些数据集发现性能与当前最优的算法有竟争性，从实验结果来看，均低于当前最优算法，因此，迫切需要提出该模型的发现性能。同时，P值的不同求解方法，对提高模型的发现效率有着显著的影响，如何构造高效的P值计算方法是提高马尔科夫边(毯)发现效率的关键，也是下一步需要努力的方向。