基于SMT的局部无嫉妒资源分配问题求解

李炳坤 陈 寅

(华南师范大学计算机科学与技术系 广东 广州 510000)

0 引 言

公平分配问题最初来源于经济学和政治学。目前在人工智能、计算机科学和应用数学等多个研究领域都得到关注。根据需要分配物品的不同，公平分配问题可以分为可分物品(divisible goods)的分配和不可分物品(indivisible goods)的分配。例如，切蛋糕问题是一个经典的可分物品的分配问题[7]，而房屋分配问题显然是一个不可分物品的分配问题[1]。对于分配是否公平也存在多种解释[9]，例如均衡性(proportional)是指对于n个Agent而言，每个Agent都认为自己分到至少1/n的物品，而无嫉妒分配(envy-free)是指每个Agent都认为自己获得的物品都不少于其他人。最近的一些研究中开始讨论Agent或者需要分配的物品之间可能存在的某种关联。例如文献[8]中讨论了物品之间存在某种依赖关系的分配问题，而文献[4]中讨论了Agent之间存在社交网络的分配问题。

在计算机科学和人工智能领域，公平分配问题的研究主要是相关问题的计算复杂度和算法实现。本文研究的问题是如何在一个社交网络中进行不可分货物的无嫉妒分配，文中对研究的问题做一些限定。假设每个Agent都对物品有不同偏好，这个偏好通过对每个物品赋一个权重来体现。这里约定权重越小对应于偏好的程度越高。每个Agent只能被分配一个物品，因此Agent的人数不能大于物品的人数。对于这类问题，如果分配是无嫉妒的，那么每个Agent都需要分配到对自己而言权重最小的物品。如果考虑到Agent处于一个社交网络中，并且只关心和它相邻的Agent分配的物品，那么在考虑无嫉妒分配的时候，情况就会有所不同。最近的研究[8]中给出这类问题的一些算法的结果。本文主要工作是给出上述分配问题求解的实现，并给出一些实验结果。

1 问题描述

假设有一个Agent的集合P={p1,p2,…,pn}和一个物品的集合G={g1,g2,…,gm}，其中n≤m。文中

规定n个Agent每人分一件物品，同时用Σ={σ1,σ2，…,σn}表示每个Agent对不同物品的偏好，其中σi(1≤i≤n)是G到N+的函数，σi(gi)的数值越小表示对于物品gi喜好程度越高。Agent之间的社交网路用无向图来表示，E是无序对{pi,pj}的集合，pi,pj∈P。本文用四元组(P,G,Σ,E)来表示一个资源分配问题。

定义1对于资源分配问题(P,G,Σ,E)，分配是一个单射函数A:P→G，表示每一个Agent分配一个不同的物品。如果对任意两个Agentpi和pj都满足σi(A(pi))≤σi(A(pj)),则称分配A是无嫉妒的(envy-free)。如果对两个Agent{pi,pj}∈E，都满足σi(A(pi))≤σi(A(pj))，则称分配A是局部无嫉妒的(local envy-free)。

显然，如果一个分配是无嫉妒的，那么它一定是局部无嫉妒的，但是在一般的情况下，无嫉妒分配是困难的。例如，考虑Agent的数量和物品数量相等，并且每个Agent对物品的评价都是严格有序的，那么除非每个Agent都被分配到最喜好的物品，否则无嫉妒分配是不存在的。如果考虑特定的社交网络下的资源分配问题，那么找到一个局部无嫉妒分配要相对容易得多，因为每个Agent只需要得到比相邻Agent更好的物品即可。

例1考虑一个为6个Agent,P={p1,p2,p3,p4,p5,p6}分配6个物品G={g1,g2,g3,g4,g5,g6}的例子。假设Agent对物品的偏好Σ={σ1,σ2,σ3,σ4,σ5,σ6}，如表1所示。

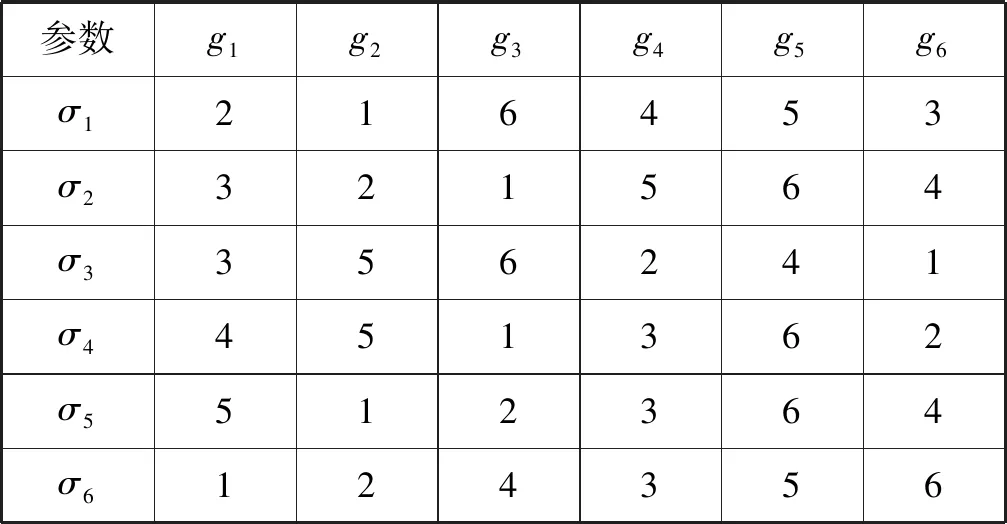
表1 Agent对物品偏好程度表

对于E1={{p1,p2},{p3,p4},{p5,p6}},可以验证分配A1:

A1(p1)=g6,A1(p2)=g3,A1(p3)=g5,

A1(p4)=g2,A1(p5)=g1,A1(p6)=g4

这是(P,G,Σ,E)的一个局部无嫉妒的分配。

给定一个社交网路，首先关心一个资源分配问题是否存在局部无嫉妒的分配。如果这样的分配不存在，那么如何找到一个分配能够使得无嫉妒的Agent最多或者Agent的嫉妒程度最小。一般而言，分为4类无嫉妒分配的问题[4]。

定义2(无嫉妒分配的存在性，EXT-LEF) 对于资源分配问题(P,G,Σ,E)，是否存在一个局部无嫉妒分配。

定义3(无嫉妒Agent最大化，MAX-AGT) 对于资源分配问题(P,G,Σ,E)，找到一个分配A使得局部无嫉妒Agent的人数最大。一个Agentpi在A下是局部无嫉妒的，如果对任意的pj，{pi,pj}∈E，都有σi(A(pi))≤σi(A(pj))。

定义4(嫉妒程度最小化，MIN-ENY) 对于资源分配问题(P,G,Σ,E)，找到一个分配A使得嫉妒程度最小。一个分配A的嫉妒程度定义为:

其中:对于{pi,pj}∈E，e(A,pi,pj)=max(0,σi(A(pi))-σi(A(pj)))。

例2在例1中，考虑E2={{p1,p2},{p1,p3},{p2,p3},{p3,p4},{p4,p5},{p4,p6}}。Agent社交网络如图1所示。

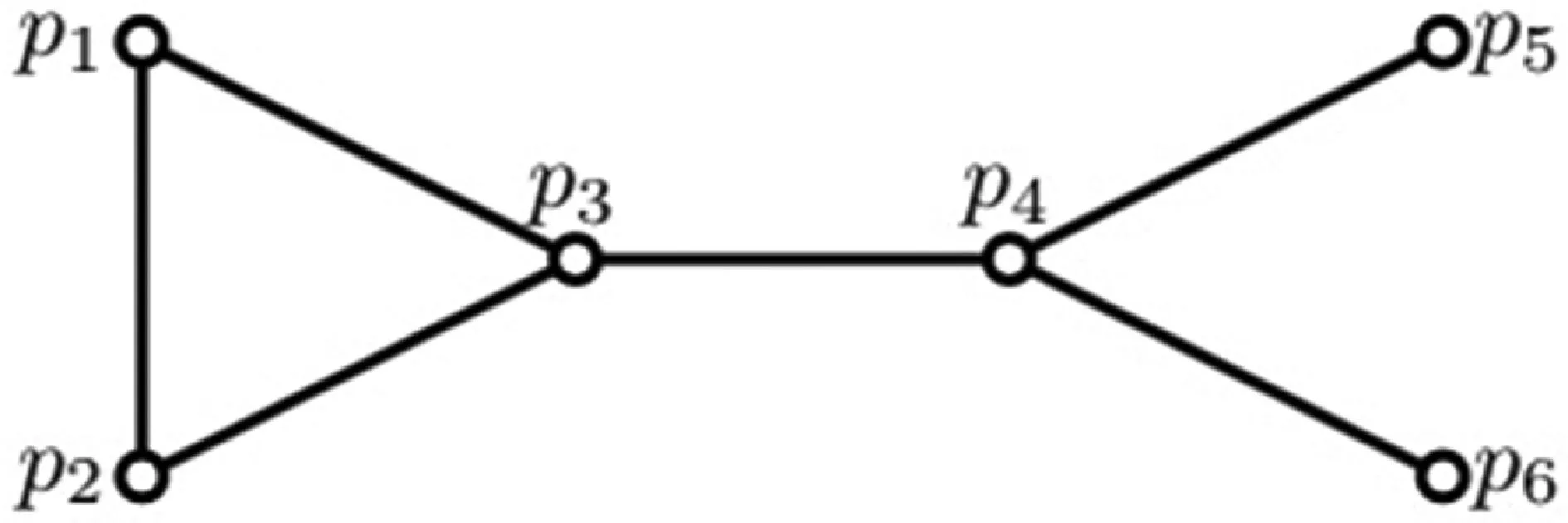
图1 Agent的社交网络

可以验证，对于EXT-LEF问题而言，(P,G,Σ,E2)是不存在局部无嫉妒分配的。

考虑分配A2:

A2(p1)=g2,A2(p2)=g3,A2(p3)=g1,

A2(p4)=g5,A2(p5)=g6,A2(p6)=g4

可以发现，A2不是一个局部无嫉妒分配，因为对于{p4,p5}∈E2，可以发现：

σ4(A2(p4))=σ4(g5)=6

σ4(A2(p5))=σ4(g6)=2

由于σ4(A2(p4))>σ4(A2(p5))，因此p4不是一个局部无嫉妒的。除了p4之外，剩余的5个Agent都是局部无嫉妒的Agent。因此A2是(P,G,Σ,E2)的一个MAX-AGT分配。

考虑分配A3:

A3(p1)=g1,A3(p2)=g3,A3(p3)=g4,

A3(p4)=g6,A3(p5)=g2,A3(p6)=g5

因为对于{p3,p4}∈E2，可以发现:

e(A3,p3,p4)+e(A3,p4,p3)=max(0,σ3(g4)-σ3(g6))+max(0,σ4(g6)-σ4(g4))=1

同时，对其余的{pi,pj}∈E2，均有e(A3,pi,pj)+e(A3,pj,pi)=0。因此分配A3的嫉妒程度为1。A3是(P,G,Σ,E2)的一个MIN-ENY分配。

定义5(重排的可能性，EXT-REL) 对于资源分配问题(P,G,Σ,E)，是否存在一个分配A和一个双射函数L:P→P，使得对任意的边{L(pi),L(pj)}∈E，都有σi(A(pi))≤σi(A(pj))。

例3对于例2中的问题(P,G,Σ,E2)，考虑双射函数L1:P→P如下:

L1(p1)=p5,L1(p2)=p4,L1(p3)=p6

L1(p4)=p1,L1(p5)=p3,L1(p6)=p2

则Agent社交网络如图2所示。

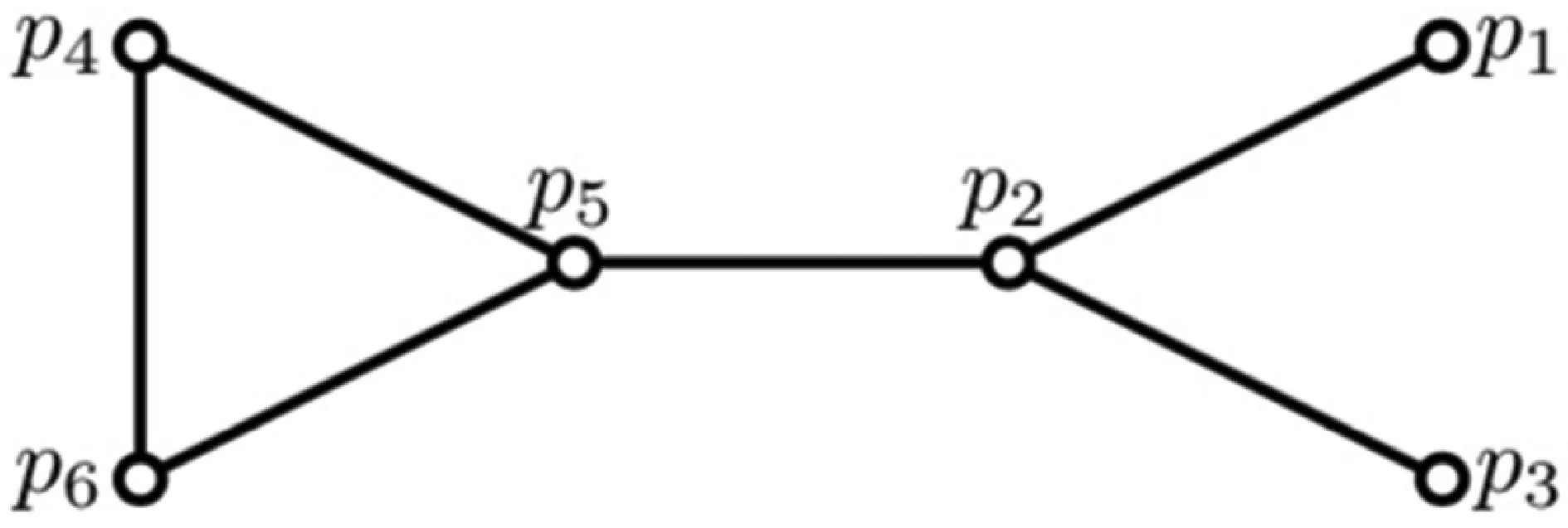
图2 Agent的社交网络

即E3={{p1,p2},{p2,p3},{p2,p5},{p4,p5},{p4,p6},{p5,p6}}。

考虑分配A4:

A4(p1)=g5,A4(p2)=g3,A4(p3)=g6,

A4(p4)=g4,A4(p5)=g2,A4(p6)=g1

可以验证，A4是(P,G,Σ,E3)的一个局部无嫉妒分配，因此(P,G,Σ,E2)存在一个EXT-REL分配。

在这4类问题中，EXT-LEF和EXT-REL是判定问题，MAX-AGT和MIN-ENY是优化问题。EXT-LEF研究给定的资源分配问题是否存在局部无嫉妒分配。MAX-AGT和MIN-ENY根据不同的目标函数来找到一个最接近局部无嫉妒分配的分配方案。EXT-REL是研究是否存在一个Agent在社交网络上的重新分布方案，使得重新分布Agent后，新的社交网络存在局部无嫉妒分配。

根据文献[4]的结果，EXT-LEF和EXT-REL是NP完全问题，即使这个社交网络是对于一些特定的图，例如线性网络、环或者是匹配图。下文将资源分配问题的求解转化为一个SMT问题。

2 基于SMT的问题求解

SMT可称为“可满足性模理论”、“多理论下的可满足性问题”或者“特定(背景)理论下的可满足性问题”(参见综述性的文献[10])，它可以被认为是一种SAT(satisfiability)的扩展。一个SMT公式是包含背景理论的逻辑公式，例如SMT公式x>1∧y<3可以认为是一个逻辑公式φ∧ψ，其中φ的真值由数学不等式x>1确定，ψ的真值由数学不等式y<3确定。通常，SMT问题是指判断一个给定的SMT公式集是否是可满足的。

SMT已经在人工智能和计算机科学的很多问题上有了广泛的应用，同时目前已经开发了很多SMT求解器用来求解SMT问题，例如Z3[5]、Yices[6]和CVC3/CVC4[2]等。输入一个SMT问题，SMT求解器可以返回这个问题是否是可满足的，对于可满足的问题还会返回一个模型。

图3说明如何使用Z3求解局部无嫉妒分配问题的模型框架。一个局部无嫉妒分配问题可转换为一些逻辑公式和约束的解释恰好对应原问题的一个解，进一步转换为SMT格式的输入，由Z3求得模型，即问题的解。

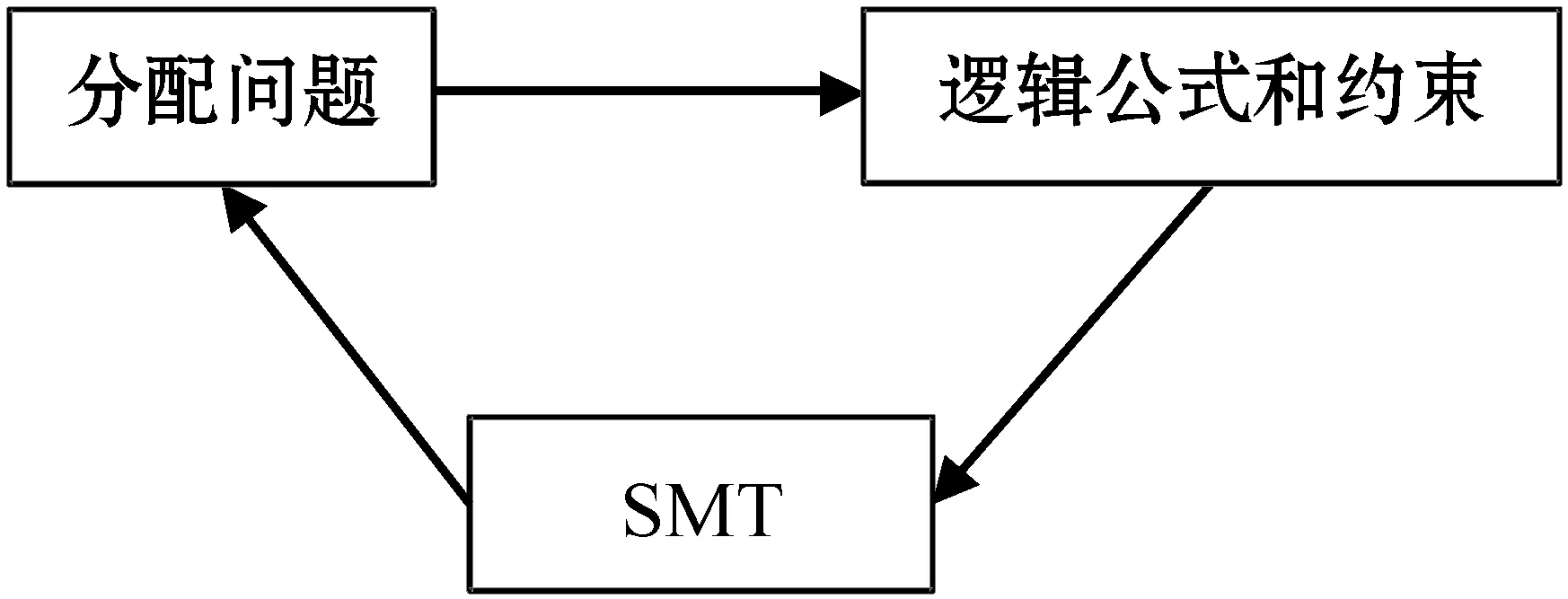
图3 Z3求解框架

下面说明如何把求解局部无嫉妒的资源分配问题转换为一个SMT问题。首先需要定义变量和约束来描述问题。考虑n个Agent和m个货物，用二元函数weight来表保存Agent对货物的偏好:

(declare-fun weight(Int Int) Int)

对于最终的分配，定义一个一元函数alloc和如下的约束:

(declare-fun alloc (Int) Int)

(assert (and (>(alloc 1) 0) (<=(alloc 1) m)))

……

(assert (and (>(alloc n) 0) (<=(alloc n) m)))

(assert (

distinct (alloc 1) (alloc 2)…(alloc m)))

其中：(alloc i)表示为Agentpi分配的物品，0<(alloci)≤m；distinct约束用来确保每个Agent分配到不同的物品。上面定义的变量和函数没有关于Agent的社交网络的信息，事实上，有关的信息是在下面添加约束的时候体现出来的。

无嫉妒分配的存在性(EXT-LEF):对每一条边{pi,pj}增加如下约束:

(assert (<=(weight i (alloc i))

(weight i (alloc j))))

(assert (<=(weight j (alloc j))

(weight j (alloc i))))

分别表示σi(A(pi))≤σi(A(pj))和σj(A(pj))≤σj(A(pi))。

无嫉妒Agent最大化(MAX-AGT):这里需要用到SMT的ite表达式。一个ite表达式形如:

(ite cond value1 value2)

其中：cond是一个逻辑公式，value1和value2为两个值。如果cond为真，则表达式的值为value1，否则表达式的值为value2。

对每一个Agentpi，假设所有包含pi的边为{pi,pj1},{pi,pj2},…,{pi,pjk}，cond_pi表示如下的逻辑公式:

(and

(<=(weight i (alloc i))

(weight i (alloc j1)))

……

(<=(weight i (alloc i))

(weight i (alloc jk)))

)

如果pi是一个局部无嫉妒的Agent，则cond_pi为真，否则为假。无嫉妒Agent最大化可以表达为如下的约束:

(maximize (sum

(ite cond_p1 1 0)……(ite cond_pn 1 0)

))

嫉妒程度最小化(MIN-ENY):对于每一条边{pi,pj}∈E，它所产生的嫉妒程度e(A,pi,pj)+e(A,pj,pi)可以表示为:

(+

(ite

(<=(weight i (alloc i))

(weight i (alloc j)))

0

(-(weight i (alloc i))

(weight i (alloc j))))

(ite

(<=(weight j (alloc j))

(weight j (alloc i)))

0

(-(weight j (alloc j))

(weight j (alloc i))))

)

假设E中有k条边，它们所产生的嫉妒程度分别是env_1,env_2,…,env_k，则嫉妒程度最小化的约束可以表示为：

(minimize

(sum env_1,…,env_k)

)

重排的可能性(EXT-REL):为了描述重排的双射函数L:P→P，定义如下的一元函数realloc和约束：

(declare-fun realloc (Int) Int)

(assert (and (> (realloc 1) 0)

(<=(realloc 1) n)))

……

(assert (and (> (realloc n) 0)

(<=(realloc n) n)))

(assert (

distinct

(realloc 1) (alloc 2)…(realloc n)

)

同时，为了从L(pi)也能得到pi，定义一个辅助的一元函数rf如下:

(declare-fun rf (Int) Int)

(declare-fun u () Int)

(declare-fun v () Int)

(assert (<=> (=(realloc u) v) (=(rf v) u)))

利用这里的约束，实际上rf恰好是realloc的反函数。

最后，对于每一条边{pi,pj}∈E，增加两个约束:

(assert (<=(weight (rf i) (alloc (rf i)))

(weight (rf i) (alloc (rf j)))))

(assert (<=(weight (rf j) (alloc (rf j)))

(weight (rf j) (alloc (rf i)))))

3 实 验

本文使用了Z3实现了基于SMT的不可分物品的局部无嫉妒资源分配问题求解。Z3是微软公司开发的一个开源的SMT求解器，也是目前最好的求解器之一。Z3不仅支持标准的SMT-LIBv2语言[3]，同时还提供了一些扩展的功能。

文中使用Z3提供的Python接口z3py实现了系统。系统的代码用Python 3.6和z3 4.8版本实现。所有的实验数据都是使用Ubuntu Linux 18.04LTS，在一台3.6 GHz的Intel i7-7700和8 GB内存的个人计算机上测得的。随机生成一些不同规模的测试用例。在实验中，总是设定Agent的人数agent_num等于物品的个数goods_num。对于相同的Agent人数和物品个数，社交网络的稠密程度对运行时间也有显著的影响。用网络中边数与相对应的完全图的边数比例edge_ratio来衡量网络的稠密程度，例如对于n个结点的社交网络，边数比例为5%的网络是相对稀疏的，它的边数为n(n-1)/2×5%。每个测试用例的超时时间设定为1 200秒。表2中，每一个运行时间都是5个随机测试用例运行时间的均值，单位为秒。如果这5个测试用例中有一个超时，则这个运行时间就设定为超时(表中为“-”)。

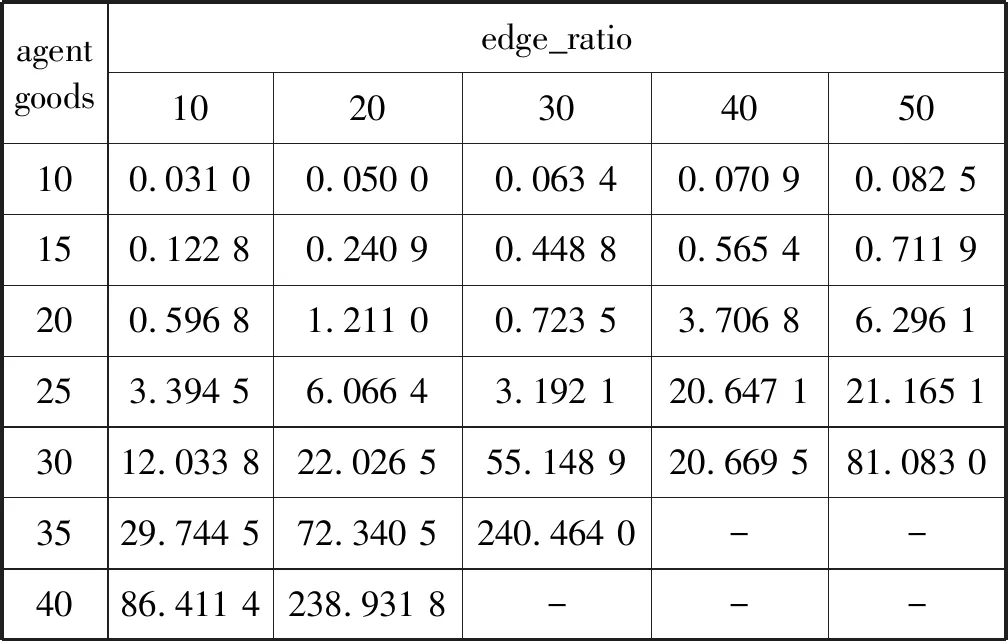
表2 测试用例平均运行时间 s

表2给出的是局部无嫉妒分配的存在性问题(EXT-LEF)的实验数据。具有运行时间的测试用例，表示存在局部无嫉妒分配。可以看出，随着Agent和物品数量的增加以及网络稠密程度的提高，运行时间有了显著的提高。另外，从原始的实验数据可以发现，对于相同的Agent数量和相同的网络稠密程度，在不同的随机测试用例上的运行时间也是可能存在很大的差别。

本文针对稀疏的网络也做了一些测试。图4是对于不同的Agent和物品的数量在边数比例分别为5%和10%下的运行时间的数据。可以看出，即使是稀疏的网络，随着Agent和物品数量的增加，运行时间增加也很快，这是由问题本身的复杂性决定的。

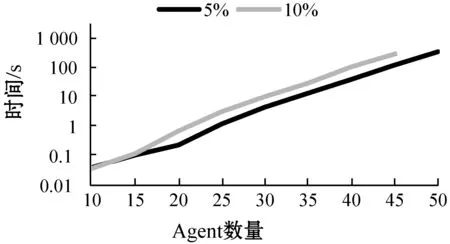
图4 稀疏网络稠密程度影响

对于MAX-AGT、MIN-ENY和EXT-REL等优化问题，需要在有局部无嫉妒分配的测试样例上进行实验。根据表2中的结果，随机产生一些Agent和物品数量在10到35之间，网络稠密程度在30%到40%之间的测试用例。这些测试用例经过EXT-LEF检测，都不存在局部无嫉妒分配。表3中给出了这些测试用例计算MAX-AGT、MIN-ENY和EXT-REL的运行时间。每一行的m-n-k表示Agent的数量，物品的数量和边数比例，随后的4个数字是相应的资源分配问题的运行时间。运行时间仍然是5个随机测试用例的均值。总体而言，与EXT-LEF相比，MAX-AGT、MIN-ENY和EXT-REL需要更长的运行时间。

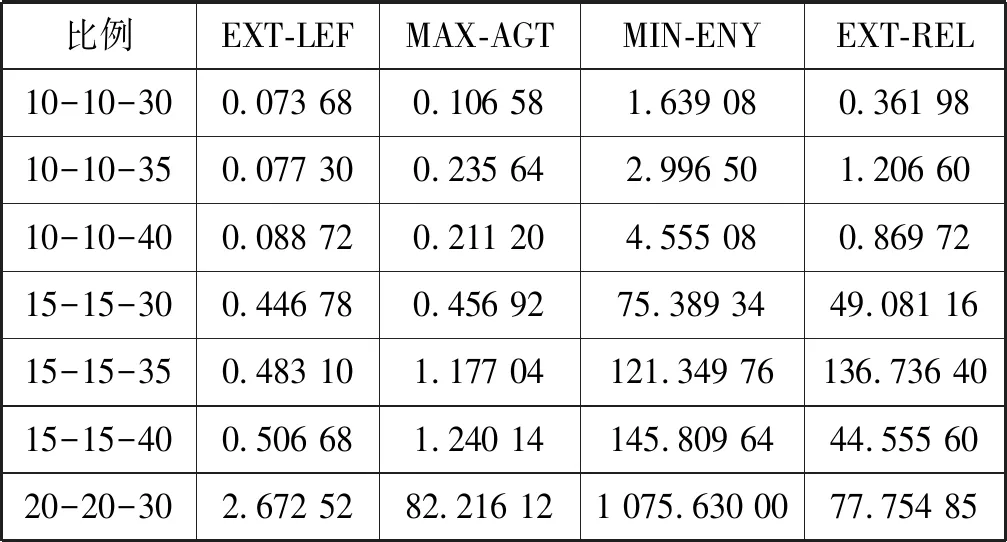
表3 局部无嫉妒分配的测试样例 s

4 结 语

本文研究了不可分物品的局部无嫉妒资源分配问题。通过把这个问题转化为SMT问题，实现一个基于Z3的系统。有关资源分配问题的相关研究主要集中于理论上的分析和有关复杂度的证明，具体的系统实现并不多见。初步尝试证明了利用SMT求解器来求解这类NP难题的可能性，同时也发现随着问题规模增长，求解的时间增长很快，特别是对于MAX-AGT和MIN-ENY这样的优化问题。

在今后的工作中，一方面可以考虑是否能够直接实现一个高效的不可分物品的局部无嫉妒资源分配问题的求解系统，与基于SMT的系统相比有何优劣;另一方面，也可以从这个问题出发，考虑SMT求解器是否有可能进行适当的优化，以提高求解这类问题，特别是优化问题的效率。