基于LDA符号表示的时间序列分类算法
武天鸿 翁小清 单中南
(河北经贸大学信息技术学院 河北 石家庄 050061)
0 引 言
时间序列通常是指按时间顺序排列而成的一组数据,任何有序的实值型数据都可以当作时间序列处理[1]。时间序列分类根据训练集中对象所构建的分类模型,判别被分类对象所属的类别[2]。时间序列分类已经被广泛应用于模式识别、医疗诊断、工业控制和异常检测等领域,时间序列数据维度高,分类难度大。
时间序列符号表示是指将连续的实值型数据表示成低维离散的符号序列数据,是一种重要的时间序列分析方法。时间序列符号表示方法不仅简单高效,对噪声具有鲁棒性,还允许学者利用来自文本处理、信息检索和生物信息学等领域的算法,对于提高时间序列分类算法的性能和效率具有重要意义。SAX(Symbolic Aggregate approXimation)[3-4]是一种经典的时间序列符号表示方法,该方法能较好地体现时间序列的整体趋势且简单高效。但是,SAX方法仅用分段的均值并不能很好地描述时间序列的局部特征,无法区分具有相同均值不同趋势的时间序列,完全不同的时间序列可能会得到相似的符号表示;SAX的MINDIST距离度量的紧性较差,容易产生误报,且该方法只适于服从高斯分布的时序数据。目前,基于符号表示的时间序列分类研究主要集中在SAX性能的改进上。在分类问题中,带有先验的分类方法能使分类性能大大提高,然而绝大多数基于符号表示的分类方法没有考虑类别的先验知识。
本文提出一种基于线性判别分析(Linear Discriminant Analysis,LDA)[5]符号表示的时间序列分类方法LDA_SC(LDA Symbolic Classification),该方法清晰地考虑了样本类别信息对符号化分类的影响,且具有自适应的符号区间分段点。LDA_SC使用线性判别分析将原始高维的时间序列数据映射到低维空间,投影后样本在低维子空间具有更近的类内距离和更远类间距离;利用信息增益在降维后的数据上寻找字符投影区间的最佳划分点,减小信息损失;定义一种新的距离度量方法,根据最近邻法对低维空间符号表示的时间序列进行分类。
1 相关研究
1.1 相关概念
本节简要介绍正交局部保持映射及信息增益的基本理论,并对基于LDA的时间序列符号表示方法进行详细介绍。
定义1时间序列。狭义上的时间序列是指一系列有时间顺序的观测值,m个观测值,n个变量的时间序列可表示为xi(t)[i=1,2,…,n;t=1,2,…,m],当n=1时,称为单变量时间序列;当n≥2时,称为多变量时间序列[6]。本文所提方法只针对单变量时间序列。
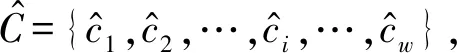
1.2 线性判别分析
时间序列维数由于随着时间不断增加,容易出现维灾现象,为了研究方便和去除噪声,需要对时间序列数据进行降维处理。线性判别分析LDA和主成分分析PCA(Principal Component Analysis,PCA)[7]是常用的两种降维方法。PCA是一种表现很好的无监督数据降维方法,各主成分之间正交,能够消除原始数据成分间的互相影响,但是如果存在方差较大的几个方向是非正交的,会造成数据不再线性可分甚至不可分。LDA是一种有监督的数据降维方法,使用类别的先验知识,将高维的数据样本投影到具有最佳可分性的子空间,使得样本在低维子空间有最大的类间距离和最小的类内距离。
假设含m个样本的数据集D={(x1,y1),(x2,y2),…,(xm,ym)},其中任意样本xi为n维向量,yi为样本xi对应的类别标签,yi∈{C1,C2,…,Ck}。首先计算所有类的样本均值u和第i类的样本均值ui,分别表示为:
(1)
(2)
式中:ni表示第i类所包含的样本个数,xij表示第i类的第j个样本。
根据u和ui计算类间散度矩阵(between-class Scatter matrix)和类内散度矩阵(within-class Scatter matrix),分别表示为:
(3)
(4)
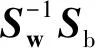
1.3 信息增益
信息增益(Information gain)[8]表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。对于分类系统而言,假设Y={(s1,y1),(s2,y2),…,(sN,yN)}是由N个“值与类标签”对组成的列表,多分类的熵定义为:
(5)
式中:pyi是标签yi在Y中出现的频率。分割点sp的熵由下式给出:
(6)
式中:YL={(si,yi|si≤sp,(si,yi)∈Y},YR={(si,yi)|si>sp,(si,yi)∈Y}。分割点sp的信息增益为:
inf_gain=Ent(Y)-Ent(Y,sp)
(7)
本文所提的时间序列符号符号化方法,使用信息增益寻找值的最佳划分点,是一种有监督的离散化方法,能够使每个分区中的大多数值对应于同一个类,可以用同一个字母表示。这种有监督的符号表示方法能够提高训练模型的分类能力。
1.4 相关研究评述
基于符号表示的时间序列分类方法,根据时间序列数据转化成符号序列的不同方式大致可以划分为4类,即基于趋势、基于聚类或进化计算、基于文本以及基于频率域的方法。针对SAX存在缺陷,学者们提出的改进方法大致可归结为从局部趋势特征描述、距离度量、符号区间划分和序列分段四个方面,不同程度地提高算法分类性能,但是也不可避免地带来一些新的问题,如参数选择困难、计算复杂度高和维数约简性能较差等。
Lkhagva等[9]提出使用每个分段的最小值、最大值和均值表示的ESAX(Extended SAX),字符串长度是SAX的三倍。Malinowski等[10]提出将每个分段(segment)的线性回归量化为字母表中一个符号的1d-SAX,该方法在分段有噪声时拟合误差较大。Yin等[11]提出根据全局关键点将长时间序列分成若干个分段,依据各分段的上升、下降和水平趋势对时间序列符号化,避免了将时间序列等长划分造成的重要信息丢失。首先将时间序列转换成比值序列或导数序列,再根据转换后序列分段的趋势特征进行符号表示的方法[12-14],在一定程度上保留原始时间序列的整体趋势变化信息,但是对于变化特征不明显的时间序列具有一定的局限。对于如何更好地划分符号区间以减少离散化过程中的信息丢失,Bai等[15]提出rSAX通过小距离调整分段点使得彼此接近的点以更高的概率映射到相同的符号。Fuad等[16]对距离查找表进行改进提出UMD,该方法以落在每个分段区间内均值的最大值和最小值作为该字母表示的边界,以边界距离作为字母间的距离构建查找表,在下界距离紧性和分类性能方面都好于SAX。Sharabiani等[17]先使用SAX将时间序列转化为符号序列,在符号序列上使用Bayesian规则和概率链规则建立模型BCM,然后用BCM对待测符号序列进行分类。然而,BCM的分类准确率与原始时间序列使用欧式距离的1NN分类的准确率差别不显著。
符号与数值混合的表示方法[18-20],虽然能够显著提高分类准确率,但是不能应用来自信息检索、文本处理和生物信息学等领域算法,应用具有局限性;基于聚类和进化计算的符号表示方法,不管数据集是否具有Gaussian分布性质都具有较好的适应性,扩展了SAX方法的适用范围,但这类方法对于合适的聚类半径、种群数量和进化代数等参数的选择是非常困难的,且所需存储空间大、计算复杂度高。
将时间序列进行符号表示后可借鉴自然语言处理中的方法进行分类,如Boer等[21]提出使用Edit距离对符号序列进行分类,Senin等[22]提出的SAX-VSM模型,Lin等[23]提出基于BOP(Bag-Of-Patterns)模型及宋伟等[24]提出其改进算法。BOP模型和SAX-VSM模型考虑了时间序列数据的整体特性和局部特性,对偏移量和噪声的影响不敏感,分类速度快且准确度高,但这类方法通常在训练阶段的时间复杂度比较高,需要的存储空间较大。
Schafer等[8]提出一种基于离散傅里叶变换(DFT)的符号表示方法SFA(Symbolic Fourier Approximation),并以SFA为基础提出不同的改进算法[25-27],SFA首先对时间序列进行离散傅里叶变换,取出前n个傅里叶系数,然后采用信息增益寻找系数的符号区间划分点,并对每一维系数使用等宽离散将其表示成符号。使用信息增益寻找符号区间划分点可减少离散过程中的信息损失,在一定程度上提高分类准确性。基于频率域符号表示的分类方法,能够有效解决分类任务中的维灾问题,而且能够在一定程度上反映时间序列的整体变化趋势,但是目前这方面的相关研究较少,主要是以SFA为基础的改进。
大多数已有方法对原始时间序列进行符号表示时,没有考虑类别的先验知识对分类性能的影响,是无监督符号化方法,然而在分类问题中,带有较为准确的先验的分类方法能使分类性能大大提高。
2 基于LDA符号表示的分类算法
2.1 符号近似表示
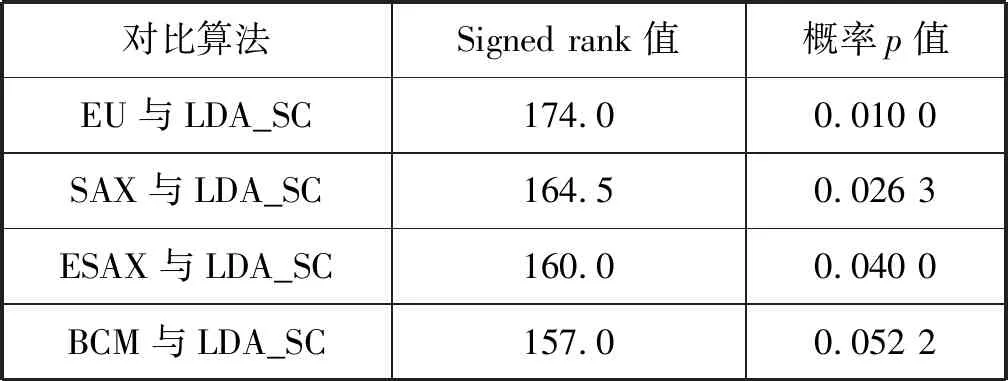
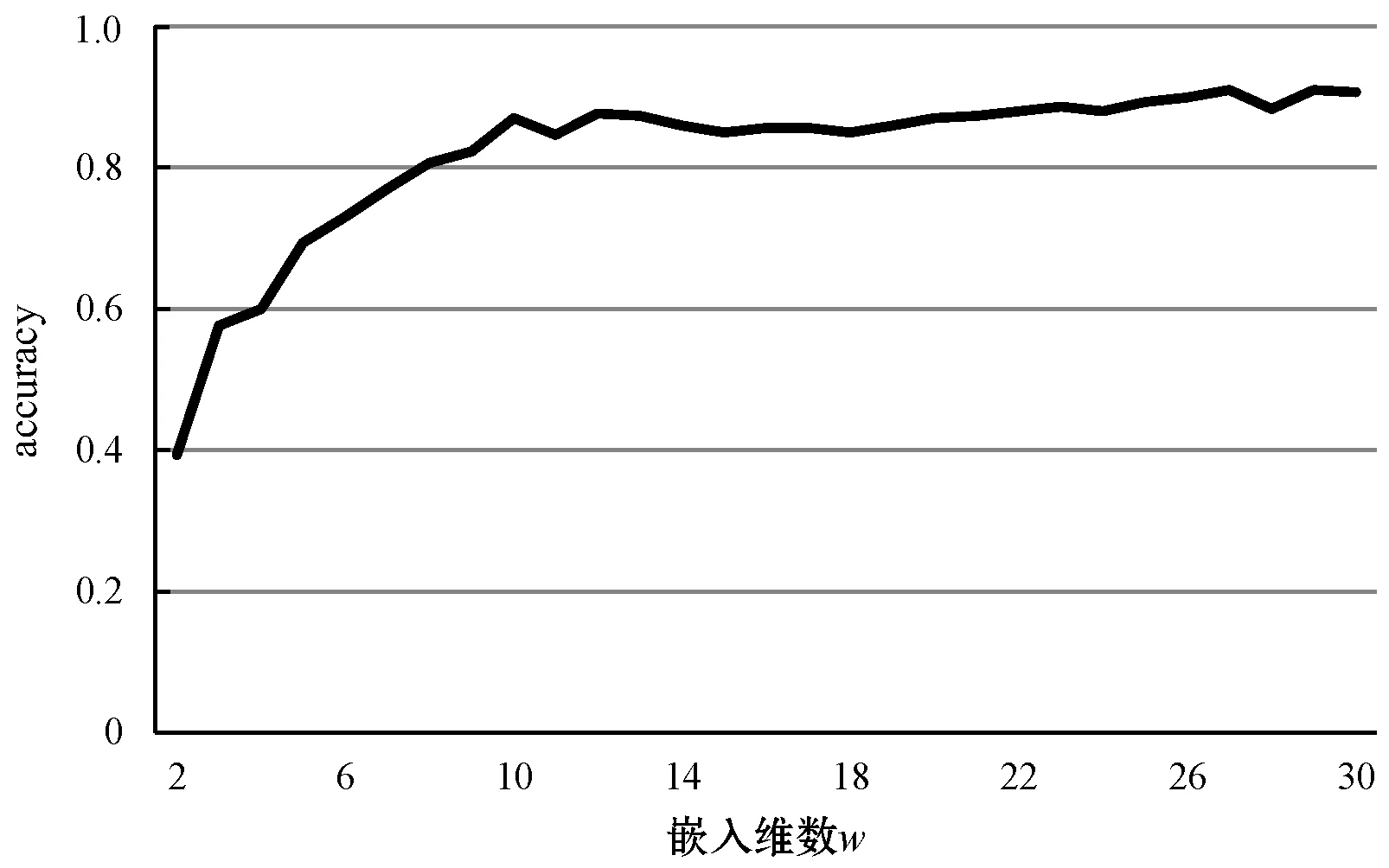
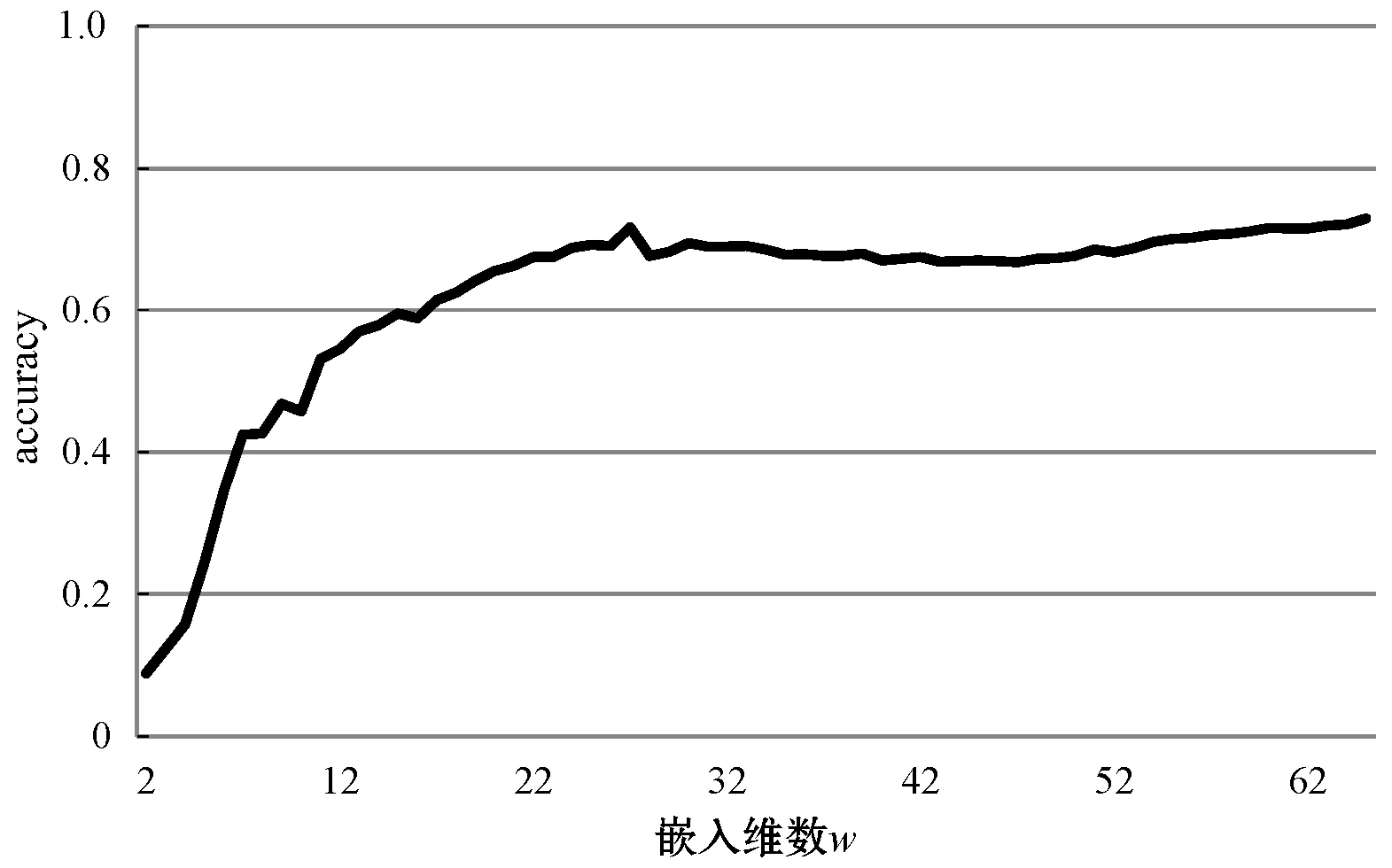
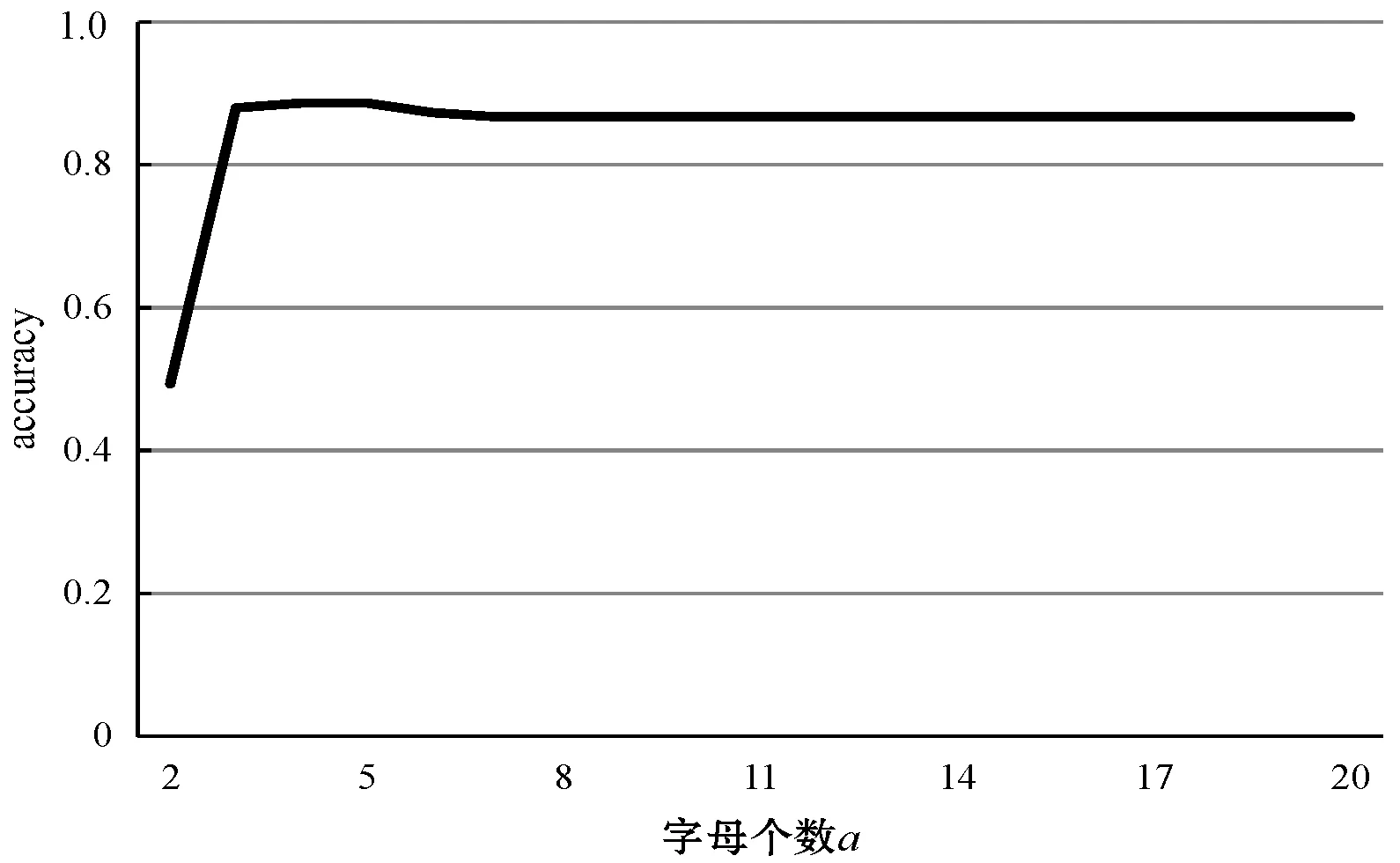
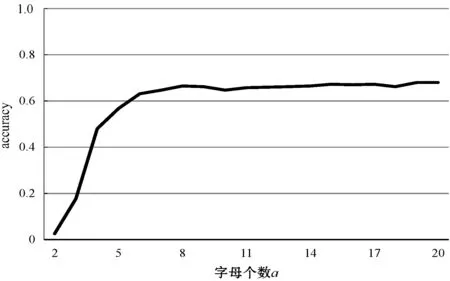
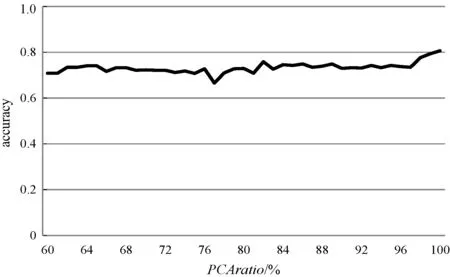
本文提出基于线性判别分析的符号近似表示方法SLA(Symbolic LDA approximation),该方法使用LDA将长度为n的时间序列降到w维(w< 图1 SLA符号近似表示过程 (8) 本文提出的基于LDA符号表示的时间序列分类算法主要包括三个步骤: (1) 使用LDA将训练集从高维空间映射到低维空间。 (2) 对降维后训练集的每一维,计算信息增益最大分割点,使得两个分割点之间的数据尽可能属于同一类别,将降维后训练样本表示成符号序列。 上述欧盟第八和第九研发框架计划预算经费比较凸显了欧盟未来7年(2021—2027)科技创新政策的着力点,即欧盟将重点资助应对全球挑战和以市场为导向的创新活动,这两块的资助经费都比“地平线2020”上浮30%~40%。尤其需要指出的是,欧盟意识到计划下大量的研发成果未能及时发挥推动经济、社会发展的价值,降低了欧盟科技计划和政策的社会影响力,所以“地平线欧洲”大大强化了对以市场为导向的高风险、颠覆性创新活动的经费支持,专设了欧洲创新理事会,形成了支持市场化创新的两个专项经费渠道,划拨专款支持创新生态系统建设,从经费和制度构建上保障创新成果从实验室走向市场,将知识资本转化为社会经济价值。 (3) 使用训练集的分割点,将低维空间的测试样本表示成符号序列,使用1NN分类器对测试样本的符号序列进行分类。基于LDA符号表示分类算法如下: LDA_SC(TRAIN,TEST,w,a,PCAratio) 输入:训练集TRAIN,测试集TEST,维数w,字母表大小a,PCA率PCAratio 输出:分类准确率accuracy Step1将TRAIN投影到PCA子空间,可调整PCAratio对原始数据降噪和消除矩阵奇异性,PCA的转换矩阵用WPCA表示; Step2根据式(1)、式(2)计算训练集的样本均值u和所有类的样本均值ui; Step3计算类间散度矩阵Sb及类内散度矩阵Sw; Step6取出低维空间中训练集的某一维数据,根据式(5)-式(7)寻找信息增益最大的分段点sp1; Step7分别在sp1前后两段数据中找出信息增益最大的分段点sp2和sp3,重复执行,直至找出(a-1)个分段点,将该维数据划分成a个区间,分别用a个不同字母表示; Step8将每个样本在该维的数据,根据其所在区间,转换为相应的字母; Step9重复执行Step 6-Step 8,直到训练集每一维数据都映射成字母,每个样本也就表示成了符号序列; Step10使用Step 5中的变换矩阵W,将TEST集样本映射到低维空间,使用TRAIN集的分段点将低维空间的测试样本表示成符号序列; Step11使用最近邻分类器,根据距离函数DIST对表示成符号序列的测试样本进行分类。 本节对LDA_SC在20个来自UCR[28]档案库的时间序列数据集上的分类性能进行评估,评估标准是分类准确率。 表1列出了20个数据集的主要特征,包括数据集名称、类别个数、训练样本总数、测试样本总数和样本长度。这些时间序列数据集主要来自生物、医学、工业控制和图像识别等领域。 表1 数据集描述 将本文提出的算法与EU(对原始数据使用欧式距离分类)、SAX、ESAX和BCM四种算法的分类性能进行比较。为了实验对照,本文将字母个数限制在2~10之间。表2和表3分别给出了使用五种方法在测试集上的分类准确率及相应参数,其中w是符号序列的长度(即低维空间的维数),a是字母表的大小,PCA ratio是LDA_SC算法中的PCA比率,五种方法的最高准确率已在表2和表3中加粗显示。 表2 EU、SAX和ESAX的分类准确率 表3 BCM和LDA_SC的分类准确率 续表3 对表2和表3中实验结果进行分析,LDA_SC在20个数据集上的平均分类准确率高于另外四种方法的平均分类准确率,且LDA_SC仅需要较少的维数就能够达到很好的分类效果;LDA_SC在15个数据集上的分类准确率高于BCM的分类准确率;LDA_SC在17个数据集上使用比SAX和ESAX更小的字母表,其中14个数据集分类准确率高于SAX,12个数据集分类准确率高于ESAX,说明LDA_SC只需要较小的字母表就能取得不错的分类效果。 从表4可以看出,LDA_SC与EU、SAX、ESAX的Wilcoxon符号秩检验的概率p值都小于0.05,说明LDA_SC的分类性能显著地好于这三种分类方法,LDA_SC与BCM的Wilcoxon符号秩检验的概率p值为0.052 2>0.05,LDA_SC与BCM差别不显著,但是从两种方法在数据集上的分类准确率来看,LDA_SC的分类效果好于BCM。 表4 Wilcoxon符号秩检验 本文提出的LDA_SC算法有3个参数,即嵌入维数w、字母表大小a和PCAratio。 图2给出在Synthetic_control数据集上,使用大小为8的字母表,当PCAratio=0.99时,准确率随嵌入维数w的变化情况。图3 给出了在Faceall数据集上,当字母表大小为8、PCAratio=0.99时,准确率随嵌入维数w的变化情况。从图2和图3中可以看出,当嵌入维数w比较小时,分类准确率比较低,随着嵌入维数w逐步增加,准确率快速上升并趋于稳定。LDA_SC仅需要较少的嵌入维数就可以获得很好的分类效果,这一良好的维数约简性能对于解决时间序列分类中的维灾问题具有重要意义,且在计算资源和存储资源较少的设备中具有适用性。 图2 准确率随嵌入维数w的变化 图3 准确率随嵌入维数w的变化(Faceall数据集) 图4给出了在Synthetic_control数据集上,当PCAratio=0.99,w=10时,准确率随字母表中字母个数的变化情况。图5给出在Adiac数据集上,当w=88、PCAratio=0.97时,准确率随字母表中字母个数的变化情况。综合图4和图5可以看出,字母个数小于3个时,准确率相对较低,字母个数在4个到8个之间就能取得较好的分类效果,随着字母个数继续增加,准确率趋于平稳。字母表的大小对LDA_SC分类性能具有较大影响,LDA_SC不需要很大的字母表就能取得较好的分类效果,存储距离查找表所占资源较少,且分类过程中的计算复杂性大大降低。 图4 准确率随字母个数a的变化 图5 准确率随字母个数a的变化(在Adiac数据集) 图6给出了在SwedishLeaf数据集上,当a=10,w=94时,准确率随PCAratio的变化情况。图7展示了在Faceall数据集上,当a=8,w=67时,准确率随PCAratio的变化情况。分析图6和图7可知,准确率在一定区域内波动,但是准确率随PCAratio增大整体呈缓慢上升趋势,PCAratio对LDA_SC的分类性能影响较小,如果PCAratio太小会造成过多的信息损失,一般在95%~100%之间取值能够使LDA_SC具有较好的分类效果。 图6 准确率随PCA ratio变化(在SwedishLeaf数据集) 图7 准确率随PCA ratio变化(在Fcaeall数据集) 本文提出一种基于LDA符号表示的时间序列分类方法。该方法在降维去噪声的同时最大化样本的类间区分度,使用信息增益寻找分段点能够尽可能地减少离散化过程中的信息丢失,在一定程度上提高分类准确性。在20个数据集上的实验结果表明,本文提出的LDA_SC分类性能显著好于已有的基于符号表示的时间序列分类方法,有监督的符号表示方法能有效提高分类性能。大部分现有方法主要针对单个时间序列样本的局部形态特征或整体趋势对其进行符号表示,没有考虑数据集样本间的近邻关系对符号化分类的影响。如何将LDA_SC算法与向量空间模型结合以及如何将LDA_SC应用于多变量时间序列的分类,仍需进一步研究。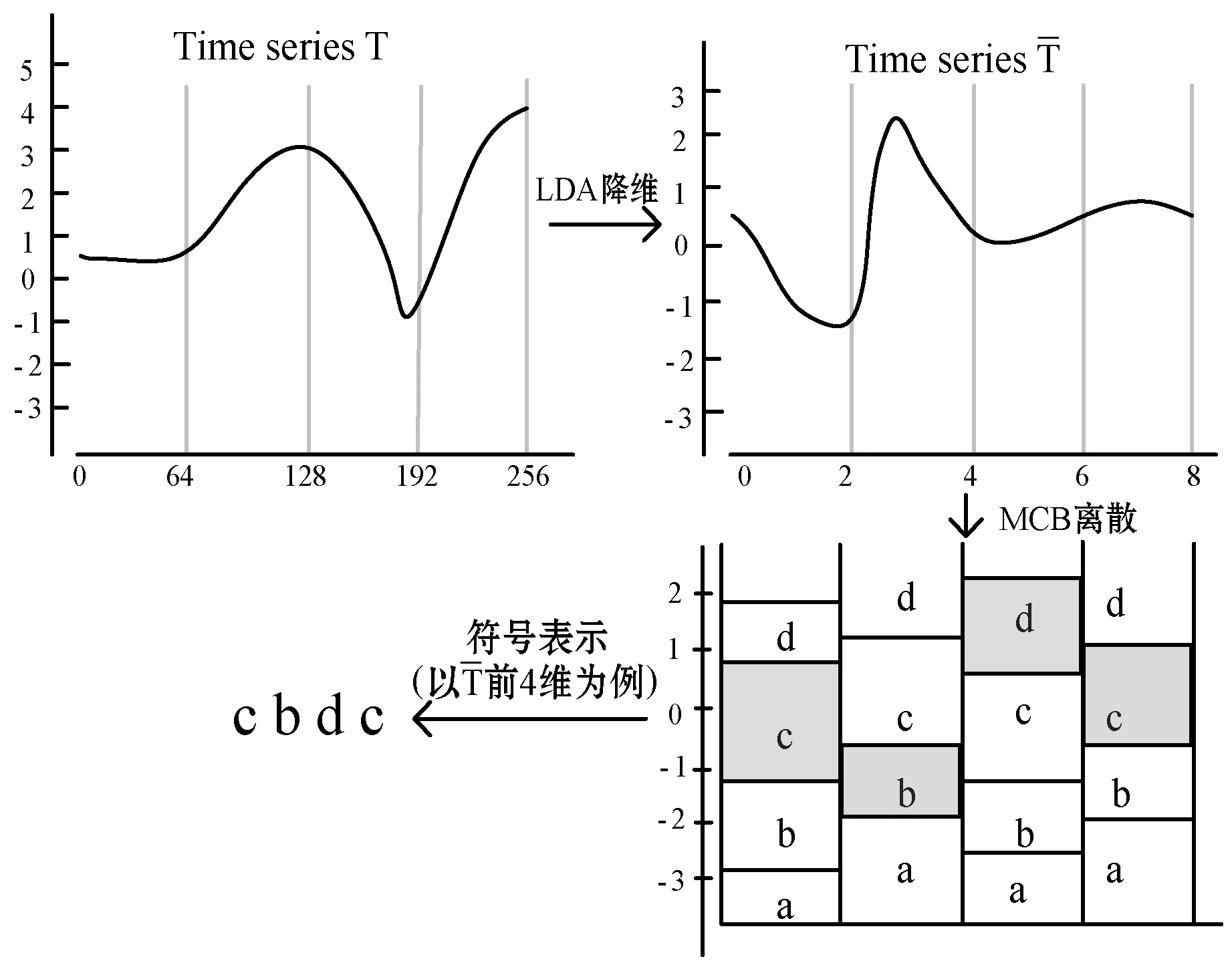
2.2 距离度量
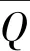

2.3 算法设计
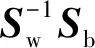
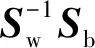
3 实验结果分析
3.1 数据集描述

3.2 性能比较

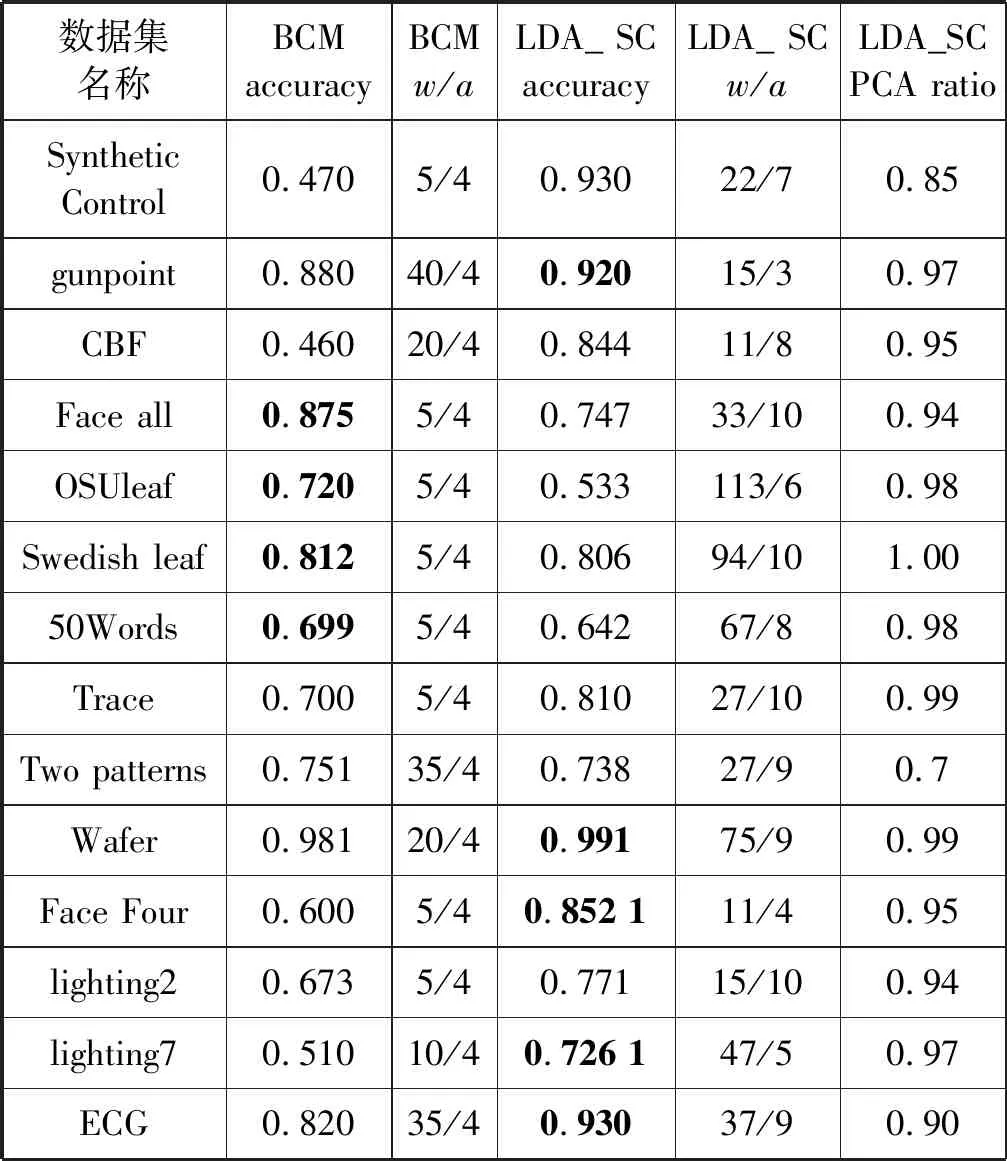
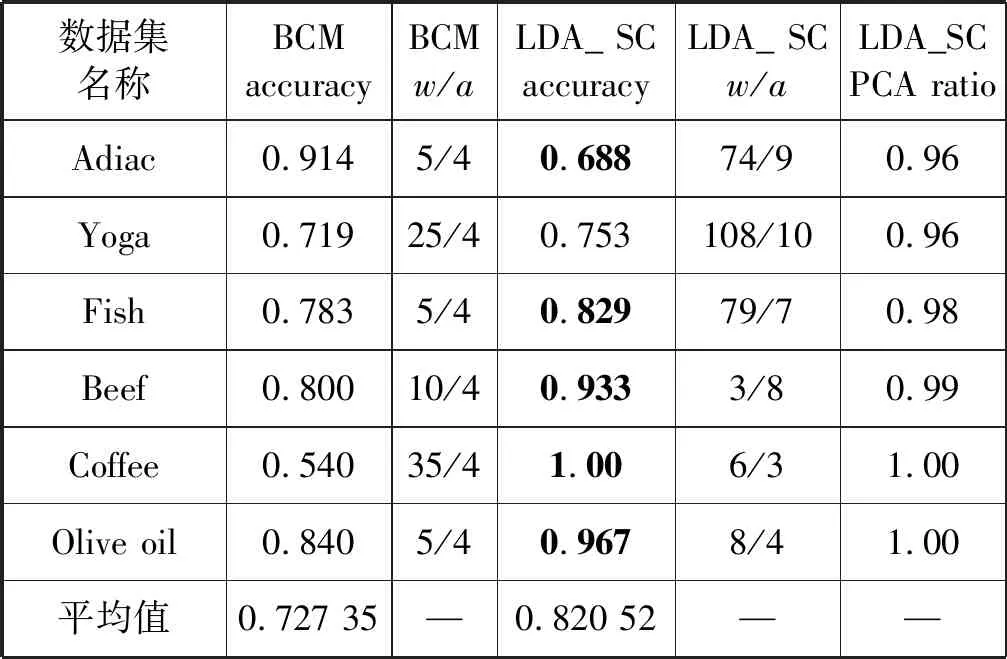
3.3 参数对分类性能的影响

4 结 语

