基于速度越界处理与最速下降法改进的蝙蝠算法
高 超 梁昔明* 龙 文
1(北京建筑大学理学院 北京 102616)2(贵州财经大学经济系统仿真贵州省重点实验室 贵州 贵阳 550025)
0 引 言
近年来,受蚂蚁、鸟类等群居生物的自组织行为的启发,一些新颖的基于仿生的元启发式算法相继出现,其中较具代表性的元启发式算法有:人工蜂群算法[1]、萤火虫算法[2]、布谷鸟搜索算法[3]、蛙跳算法[4]、蝙蝠算法[5]。
蝙蝠算法是剑桥学者YANG教授在2010年基于蝙蝠的回声定位特性提出的一种优化算法。蝙蝠算法主要通过改变声音的响度、脉冲发射频率和脉冲频率来搜索最佳蝙蝠的位置。目前BA广泛应用于各个领域,如:Alemu等[6]将BA应用于燃气轮机发电系统模型中;Yang等[7]使用BA解决拓扑优化问题中的弹簧问题和减速器问题;Gandomi等[8]利用BA算法求解3个基准工程约束优化问题;还有一些学者将其应用于工程设计[9]、模糊聚类[10]、资源调配[11]等领域。但是从BA本身的迭代机制而言,当寻优区域较大时,BA存在着收敛于全局最优解的速度缓慢、收敛精度不高、易陷入局部极值等不足,这些都影响着BA应用。所以,针对这些问题,学者们提出了很多改进的BA,如谢健等[12]提出了一种基于Levy飞行轨迹的蝙蝠算法;高珊等[13]提出了函数优化的小生境蝙蝠算法;肖辉辉等[14]提出了基于DE算法改进的蝙蝠算法等。但上述几种改进的BA也普遍存在着收敛精度不高、易陷入局部最优的问题。基于上述问题,本文提出一种基于速度越界处理与最速下降法改进的蝙蝠算法(VCBA)。实验表明,VCBA在收敛精度和稳定性上都有较大的提高。
1 蝙蝠算法
对无约束连续优化问题:
minf(X)X∈Rn
若X∈Rn满足
f(X*)≤f(X) ∀X∈Rn
X*为f(X)在全空间Rn上的全局极小点。
蝙蝠算法的迭代流程如下:
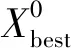
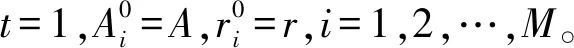
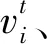
Fi=Fmin+(Fmax-Fmin)×β
(1)
(2)
(3)
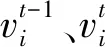
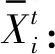
(4)
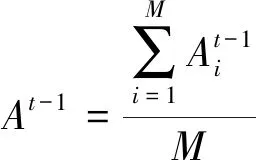

(5)
(6)
(7)
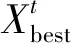
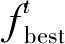
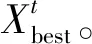
2 改进蝙蝠算法设计
2.1 速度的越界处理
文献[5]指出,蝙蝠算法是一种特殊的标准粒子群算法,又由文献[15]可知,粒子群算法中的粒子速度需要进行越界处理,这是为了使粒子在解空间中能够均匀而全面的分布,使粒子群算法的搜索范围更广。在改进的蝙蝠算法中,对蝙蝠速度同样需要进行越界处理。
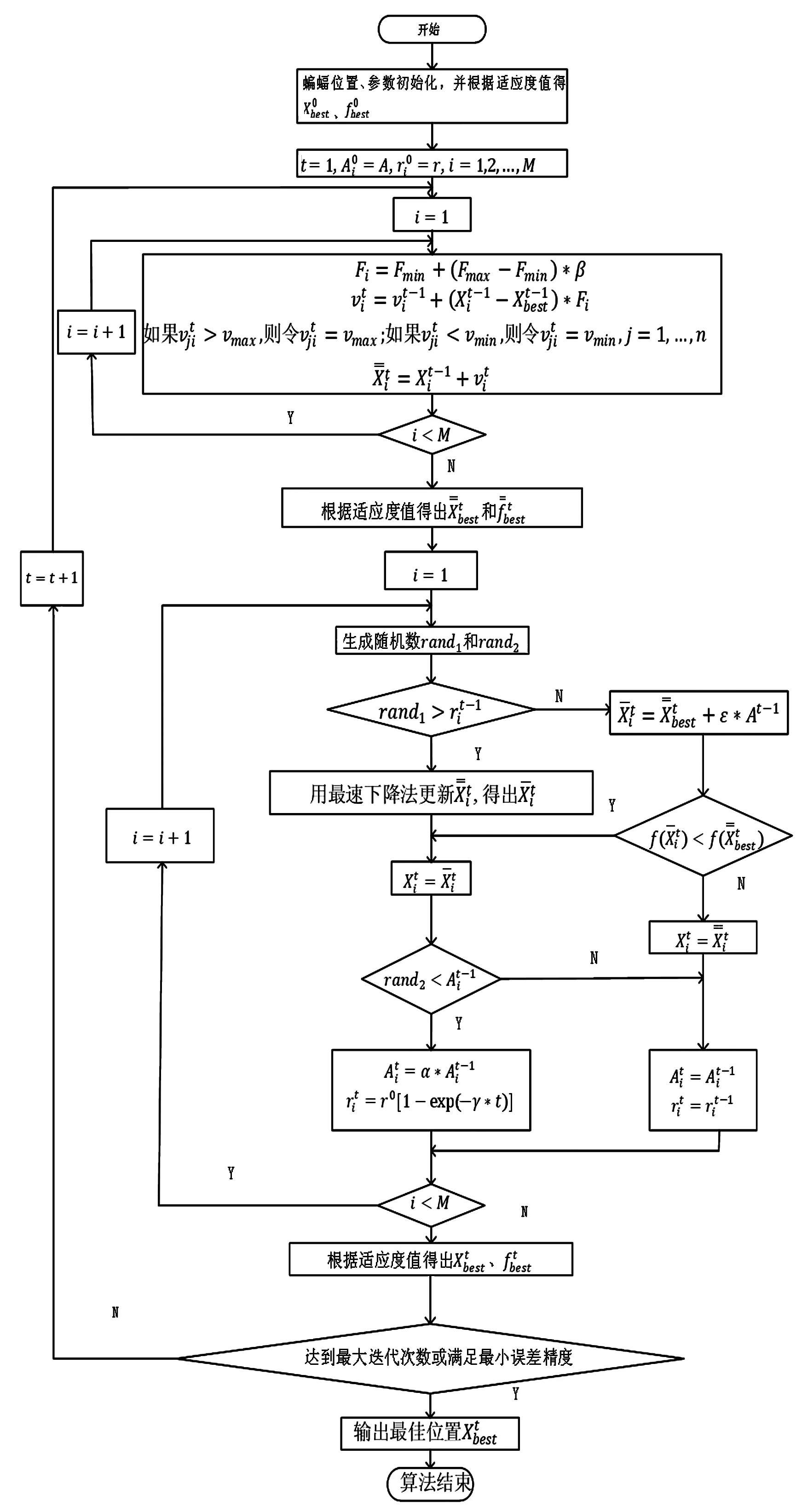
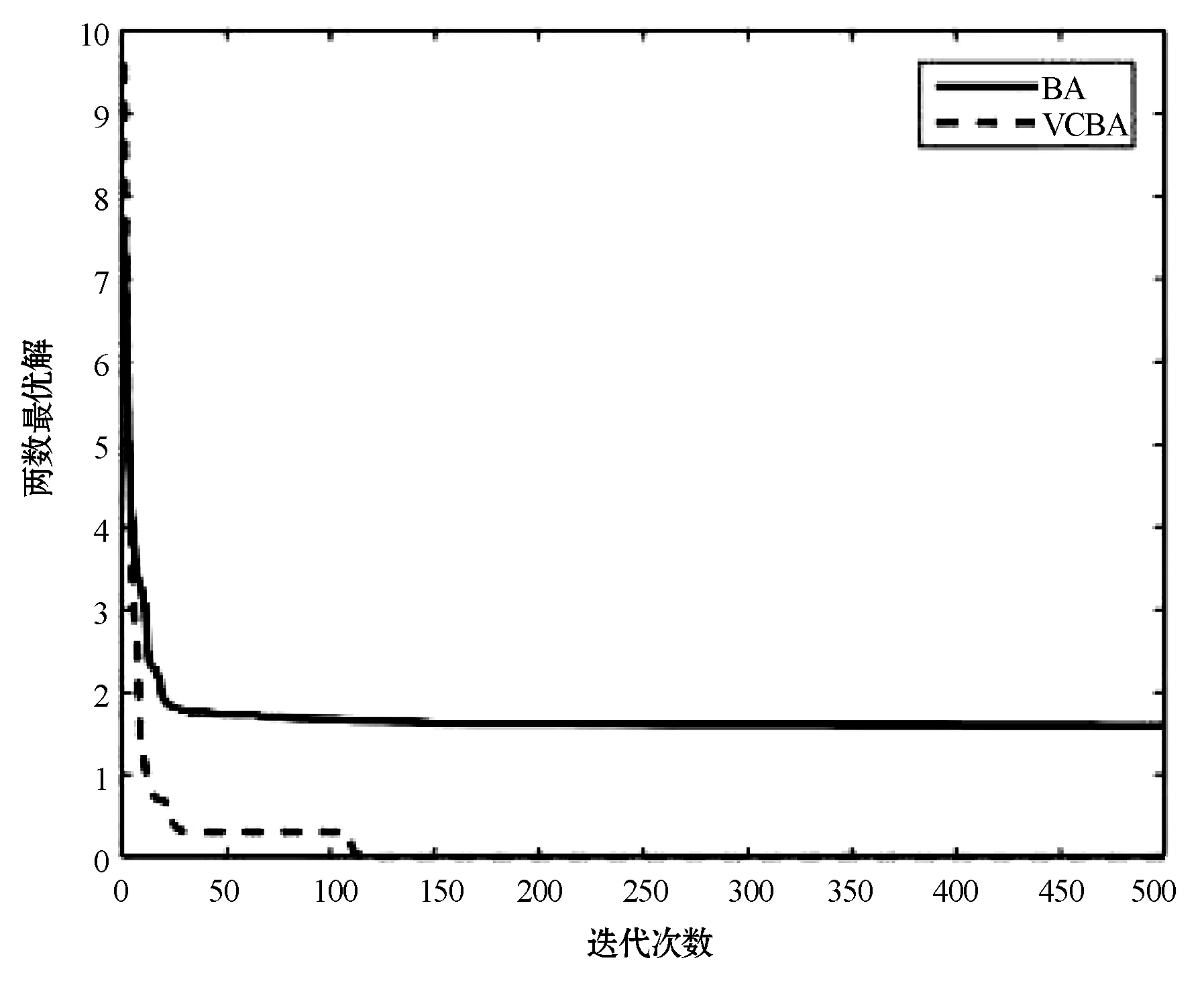
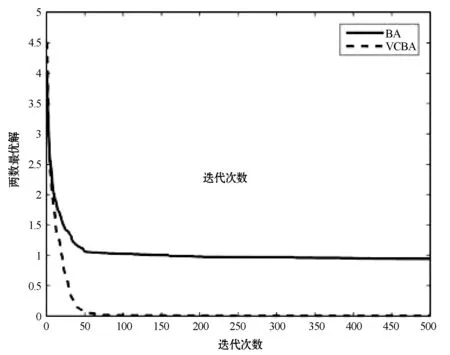
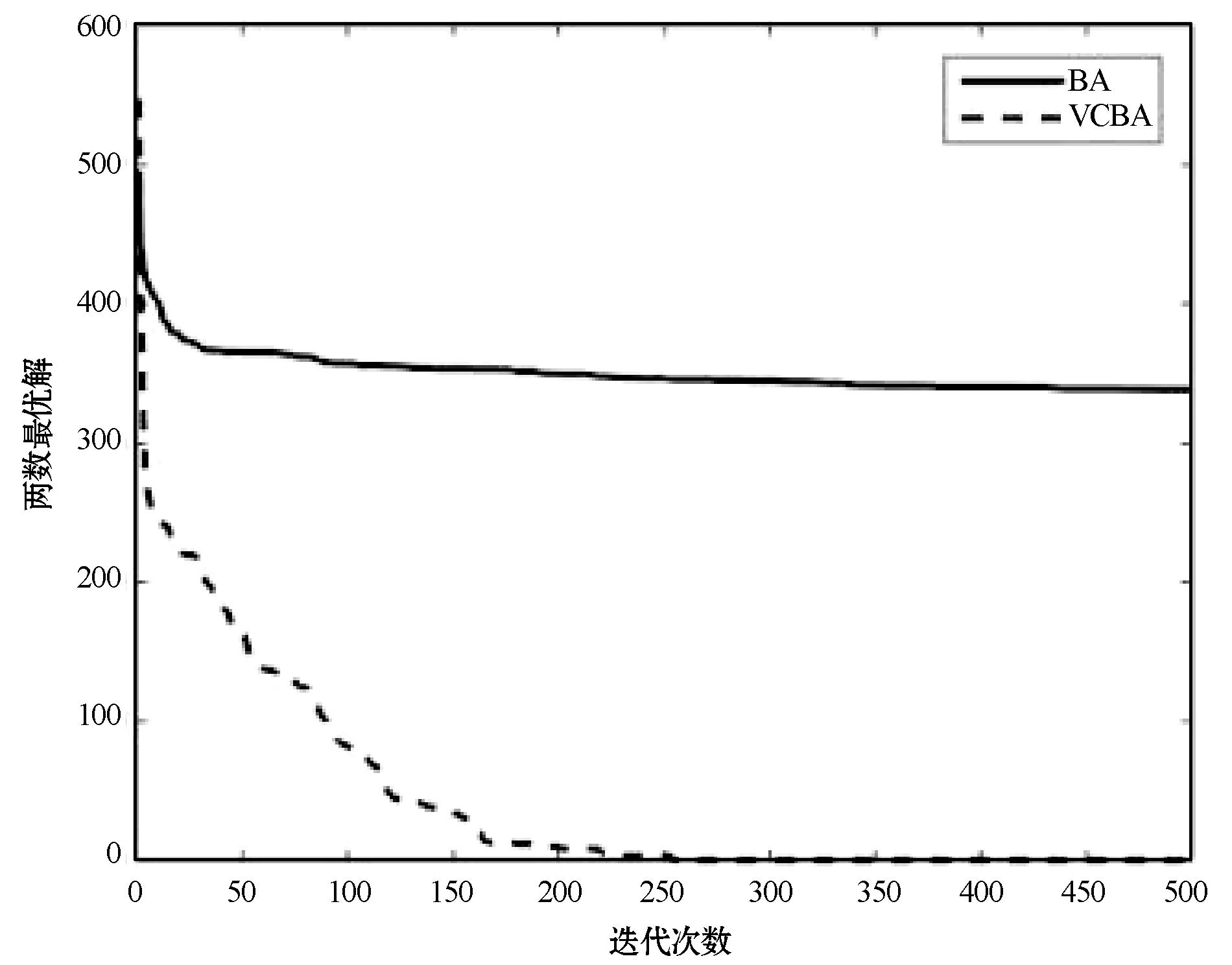
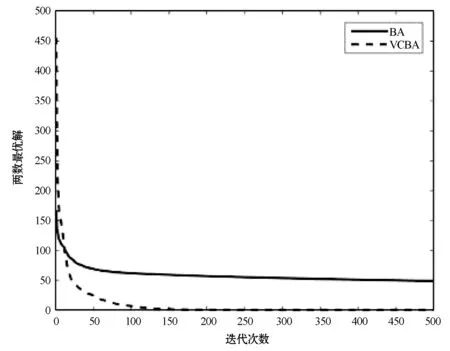
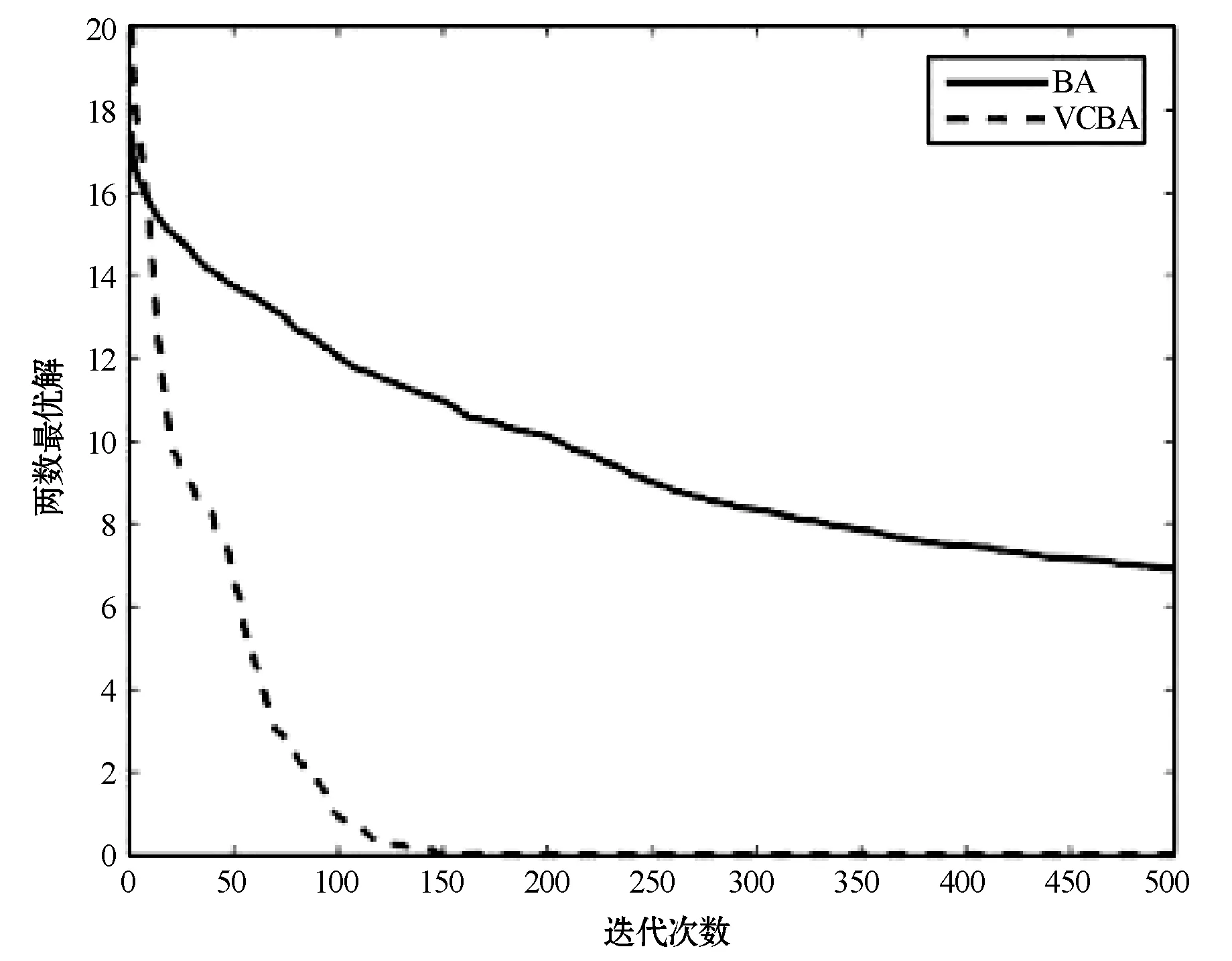
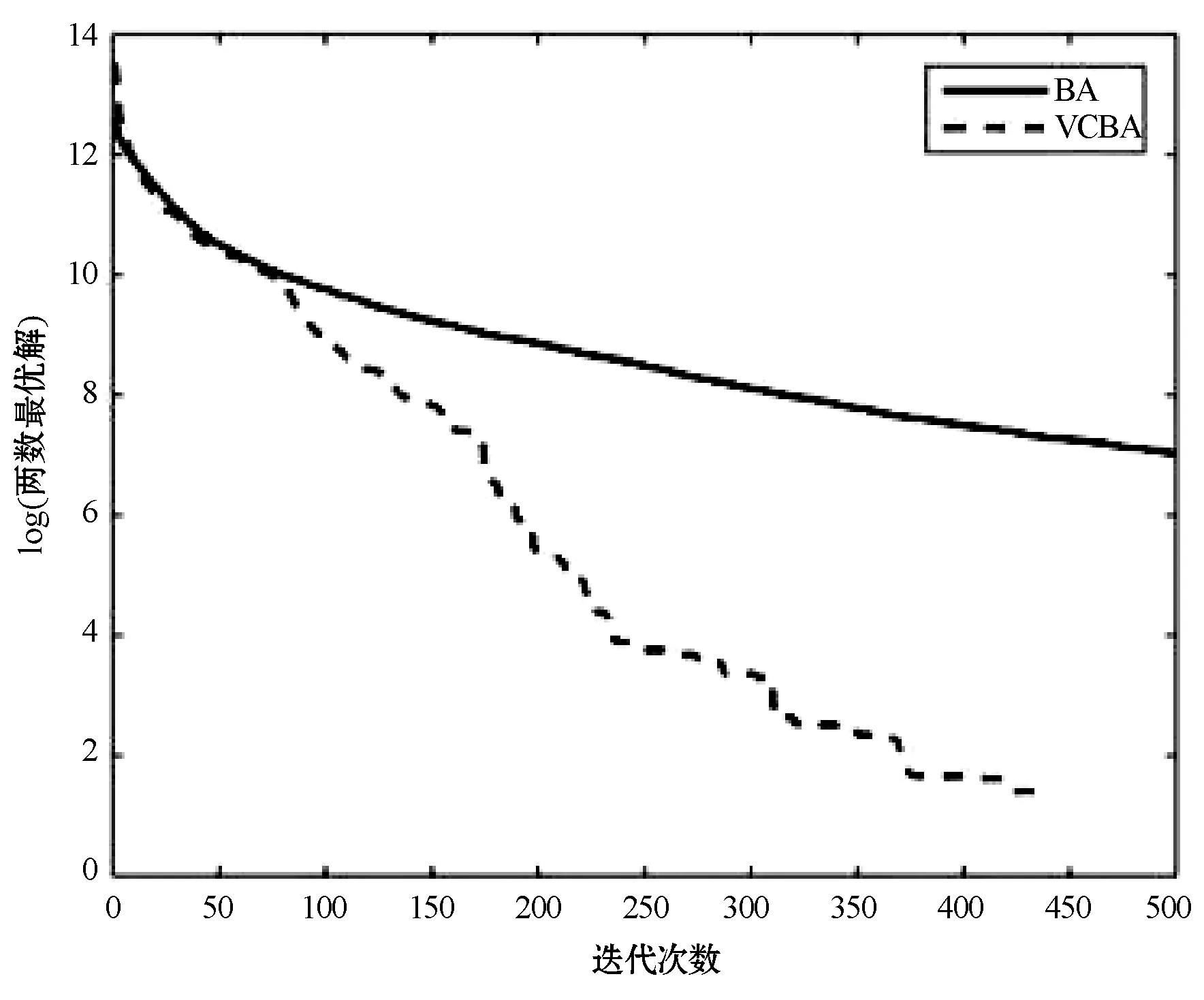
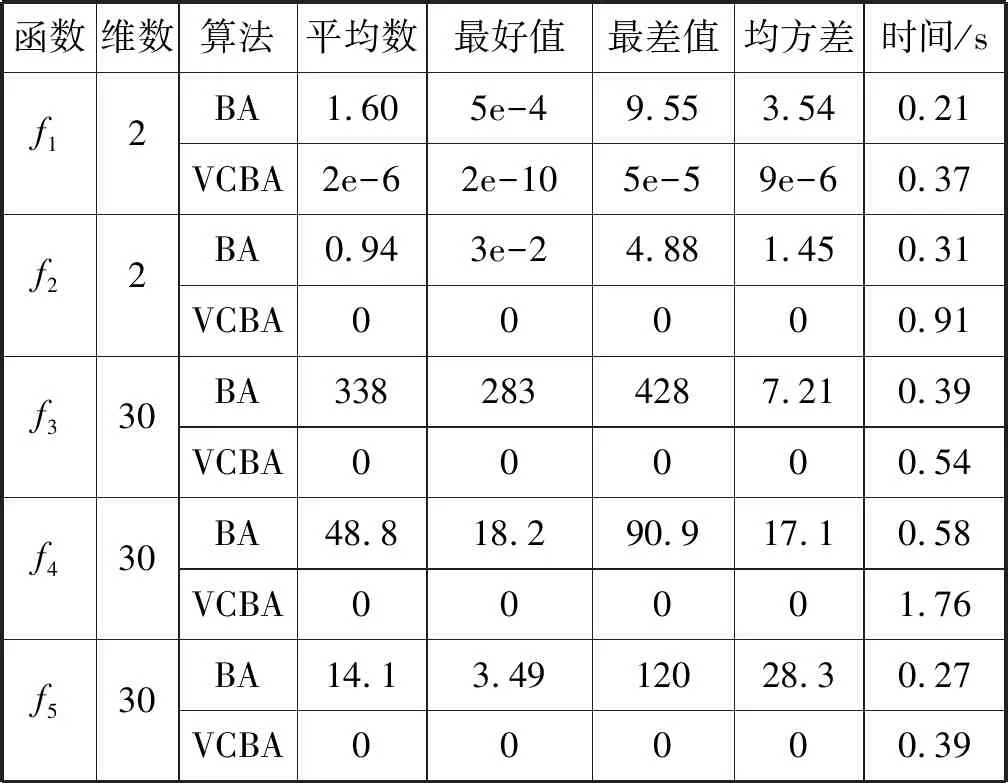
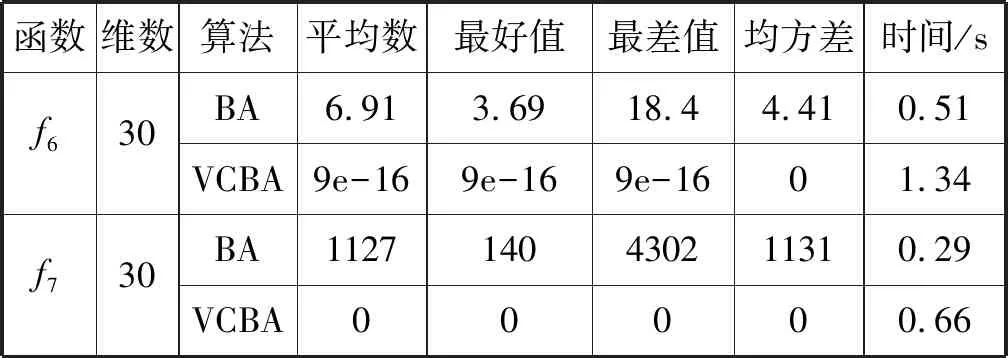
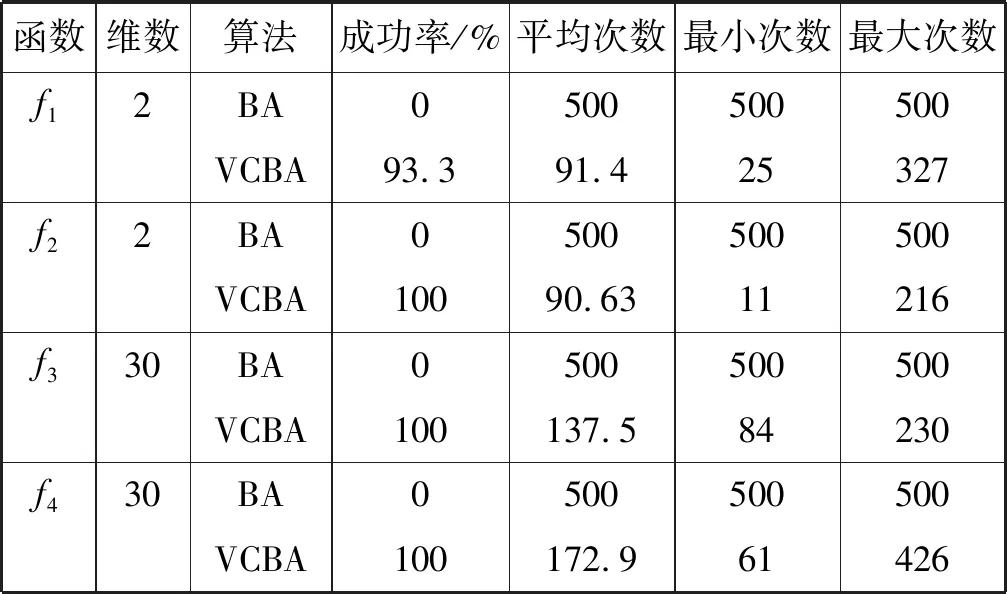
在改进的蝙蝠算法中,对蝙蝠速度的越界处理采用如下方法:对v=(v1,v2,…,vn)T,如果vj>vmax,则令vj=vmax;如果vj 在改进的蝙蝠算法中将速度范围控制在蝙蝠位置的范围以内,即vj∈[vmin,vmax]⊆[Xmin,Xmax],j=1,2,…,n,这样能够控制蝙蝠位置更新的幅度不会太大,具体的速度范围需要实验确定。经实验测试,本文取vmin=-5,vmax=5。若所选取的测试问题的范围小于速度范围,则令vmin=Xmin,vmax=Xmax。 1847年数学家Cauchy提出了最速下降法[16],是求解无约束优化问题最简单的方法之一。最速下降法是用负梯度方向作为搜索方向,其步长一般由线性搜索方法来确定。由于负梯度方向是函数的局部最速下降方向,所以若从某一点出发,用最速下降法进行迭代,得到的点一定比原来的点更优,不会出现无价值迭代。最速下降法的优势在于算法简单,而且从一个不好的初始点出发,往往也能收敛到局部最优值,具有快速精细的局部搜索能力。 p0=-g(X0) (8) (9) (10) (11) (12) (13) (14) 改进的蝙蝠算法步骤如下: 第1步执行BA的第1步。 第2步执行BA的第2步。 (15) (16) 第5步执行BA的第6步。 第6步执行BA的第7步。 改进的蝙蝠算法(VCBA)的流程图如图1所示。 图1 改进的蝙蝠算法流程图 为了验证VCBA的寻优效果,使用7个基准测试优化问题进行数值实验。各测试优化问题的目标函数的表达式、搜索范围和理论最优值如下: 实验中,参数设置如下:M=25;maxgen=500;α=0.95;γ=0.05;A=0.95;r=0.9;脉冲频率最小值Fmin=-1,脉冲频率最大值Fmax=1;误差精度tol=1e-6。 BA和VCBA对目标函数f1-f7各独立求解30次,所得目标函数值的平均进化曲线如图2-图7所示,图8表示所得目标函数值的平均值取以10为底的对数所得的进化曲线。 图2 f1的平均进化曲线 图3 f2的平均进化曲线 图4 f3取30维时的平均进化曲线 图5 f4取30维时的平均进化曲线 图6 f5取30维时的平均进化曲线 图7 f6取30维时的平均进化曲线 图8 f7取30维时的平均进化曲线 由图2可以看出,对2维的f1函数,BA大概在20次迭代后陷入局部极值,而VCBA大概在迭代110次后接近全局最优值;由图3可以看出,对2维的f2函数,BA大概在50次迭代后陷入局部极值,而VCBA大概在60次迭代后接近全局最优值;由图4可以看出,对30维的f3函数,BA大概在迭代50次后陷入局部极值,而VCBA大概在迭代250次后接近全局最优值;由图5可以看出,对30维的f4函数,BA大概在20次迭代后陷入局部极值,而VCBA大概是在迭代100次后接近全局最优值;由图6可以看出,对30维的f5函数,BA大概在迭代250次后陷入局部极值,而VCBA大概是在迭代5次后接近全局最优值;由图7可知,对30维的f6函数,BA大概在300次迭代后陷入局部极值,而VCBA大概是在150次迭代后接近全局最优值;由图8可知,对30维的f7函数,BA大概在400次迭代后陷入局部极值,而VCBA大概是在450次迭代后接近全局最优值。 BA与VCBA对目标函数f1-f7独立求解30次,所得各方面数据对比如表1所示。 表1 在固定迭代次数下的数据对比 续表1 由表1可知,在独立求解30次的情况下,对目标函数f1-f7,BA算法都得不到相应函数的理论最优值或达到较高的精度。对2维的目标函数f1,VCBA在独立求解30次后,所得30个目标函数值的平均值、最好值、最差值的精度分别能达到1e-6、1e-10、1e-5,且所得均方差的精度能达到1e-6,比BA得到的结果更稳定,VCBA的运行时间不到BA的2倍;对2维的目标函数f2,以及30维的目标函数f3、f4、f5、f7,VCBA独立求解30次后,所得30个目标函数值的平均值、最好值、最差值都能达到它们的理论最优值0,且所得均方差为0,比BA得到的结果稳定,VCBA的运行时间不到BA的4倍;对30维的目标函数f6,VCBA独立求解30次后,所得30个目标函数值的平均值、最好值、最差值的精度都能达到1e-16,且所得均方差为0,比BA算法得到的结果要稳定,VCBA的运行时间不到BA的3倍。 由上述分析可知,在固定迭代次数为500的情况下,算法VCBA的运行时间虽然比BA耗费的时间要更长,但VCBA所得目标函数值的精度高于BA,且求解更加稳定。 在给定目标函数值的精度为1e-6的情况下,BA和VCBA独立求解目标函数f1-f730次所需的迭代次数如表2所示,其中成功率表示达到给定目标函数值精度的次数除以独立求解次数30,算法若迭代500次仍没有达到给定的目标函数值精度,则终止迭代,此时认为算法求解问题失败。 表2 算法达到目标函数值精度所需的迭代次数 续表2 由表2可知,在指定收敛精度下,对目标函数f1-f7,BA不能在500次迭代后达到所给定精度,即BA对7个目标函数的成功率为0。对2维目标函数f1,VCBA算法的成功率为93.333%,且最小迭代次数不到30次;对2维目标函数f2以及30维的目标函数f3-f7,VCBA的成功率为100%,且最小迭代次数不到100次,其中对目标函数f5的求解,平均迭代次数不到5次。 由上述分析可知,在给定目标函数值精度的情况下,不管目标函数是低维还是高维,VCBA的求解成功率相较于BA都有明显优势。 其他文献中大多用目标函数f3-f6对算法性能进行对比分析,本文同样使用目标函数f3-f6对VCBA与三种优化算法进行对比。三种算法分别为基本粒子群算法PSO,基于频率简化的自适应蝙蝠算法FSABA,基于自适应步长的改进蝙蝠算法SABA。实验中,参数设置如下:种群数M=40,最大迭代次数maxgen=500次,目标函数维数n=30,其余参数设置同3.1节,对每个目标函数,各算法均独立求解50次,所得目标函数值的结果如表3所示,除VCBA外,另三种算法的结果均来自文献[17]。 表3 固定迭代次数下VCBA与 三种优化算法所得函数值 续表3 由表3可知,对目标函数f3-f5,三种优化算法在50次独立求解中均达不到对应目标函数的理论最优值0,而VCBA在50次独立求解中,其得到的最好值、最差值以及平均值都能达到对应目标函数的理论最优值0;对目标函数f6,PSO以及FSABA在50次独立求解中,得到的最好值、最差值以及平均值的精度都在1e+1以上,SABA得到的最好值、最差值以及平均值的精度都为1e-10,而VCBA得到的最好值、最差值以及平均值的精度都为1e-16。 由上述分析可知,VCBA在目标函数寻优精度和稳定性方面相比于PSO、FSABA及SABA算法有较大优势。 在蝙蝠算法的迭代机制中,响度A的初始值A0和脉冲发射频率r的初始值r0的取值与算法效果的好坏息息相关。所以本文将验证不同的(A0,r0)取值对VCBA的影响。具体方法如下:在固定迭代次数的情况下,分析五组不同的(A0,r0)对VCBA的影响。这里我们选取4个多峰函数f3、f4、f6、f7作为目标函数,(A0,r0)的五组不同取值为:(0.5,0.01)、(0.9,0.5)、(0.95,0.9)、(1,rand)、(0.25,0.75),设置最大迭代次数maxgen=500,目标函数维数n=30,其余参数设置同数值实验3.1,对每个目标函数,用VCBA独立求解30次,所得函数值如表4所示。 表4 参数(A0,r0)不同取值时所得目标函数值 续表4 由表4可知,对目标函数f3,当(A0,r0)取(0.5,0.01)时,VCBA在30次独立求解中均达不到对应目标函数的理论最优值,当(A0,r0)取(0.9,0.5)、(1,rand)、(0.25,0.75)时,VCBA有时能达到目标函数的理论最优值0,当(A0,r0)取(0.95,0.9)时,VCBA在30次独立求解中得到的平均值、最好值、最差值都达到目标函数的理论最优值0;对目标函数f4、f7,当(A0,r0)取(0.5,0.01)、(0.9,0.5)时,VCBA在30次独立求解中均达不到对应目标函数的理论最优值0,当(A0,r0)取(1,rand)、(0.25,0.75)时,VCBA有时能达到目标函数的理论最优值0,当(A0,r0)取(0.95,0.9)时,VCBA在30次独立求解中得到的平均值、最好值、最差值都能达到目标函数的理论最优值0;对目标函数f6,当(A0,r0)取(0.5,0.01)时,VCBA在30次独立求解中均达不到对应目标函数的理论最优值0,当(A0,r0)取(0.9,0.5)、(1,rand)、(0.25,0.75)时,VCBA有时能达到1e-16的精度,当(A0,r0)取(0.95,0.9)时,VCBA在30次独立求解中得到的平均值、最好值、最差值的精度都能达到1e-16。 由上述分析可知,当(A0,r0)取(0.95,0.9)时,VCBA对于选取的4个多峰目标函数有较好的寻优效果。 本文在基本BA的基础上提出了一种基于速度越界处理与最速下降法的改进蝙蝠算法(VCBA)。VCBA的特点在于速度的越界处理能够有效地控制蝙蝠位置扰动的范围。在蝙蝠进行局部搜索时,对当前不好的蝙蝠位置用最速下降法进行确定性的邻域搜索,降低随机性;对BA判断局部搜索阶段产生的蝙蝠位置是否满足要求的条件进行改进,保留了最速下降法更新的蝙蝠位置。数值实验结果表明,相比于基本BA、两种改进的BA和PSO,VCBA在收敛精度和稳定性方面都有很大的优越性。如何将BA与其他优化算法进行有机融合是我们进一步研究的主要工作。2.2 最速下降法
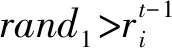
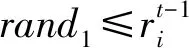
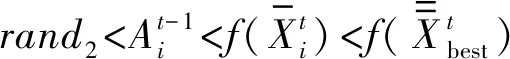
2.3 改进算法步骤

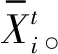
3 数值实验
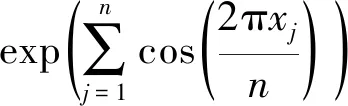
3.1 固定迭代次数的数据对比

3.2 给定精度下所需的迭代次数

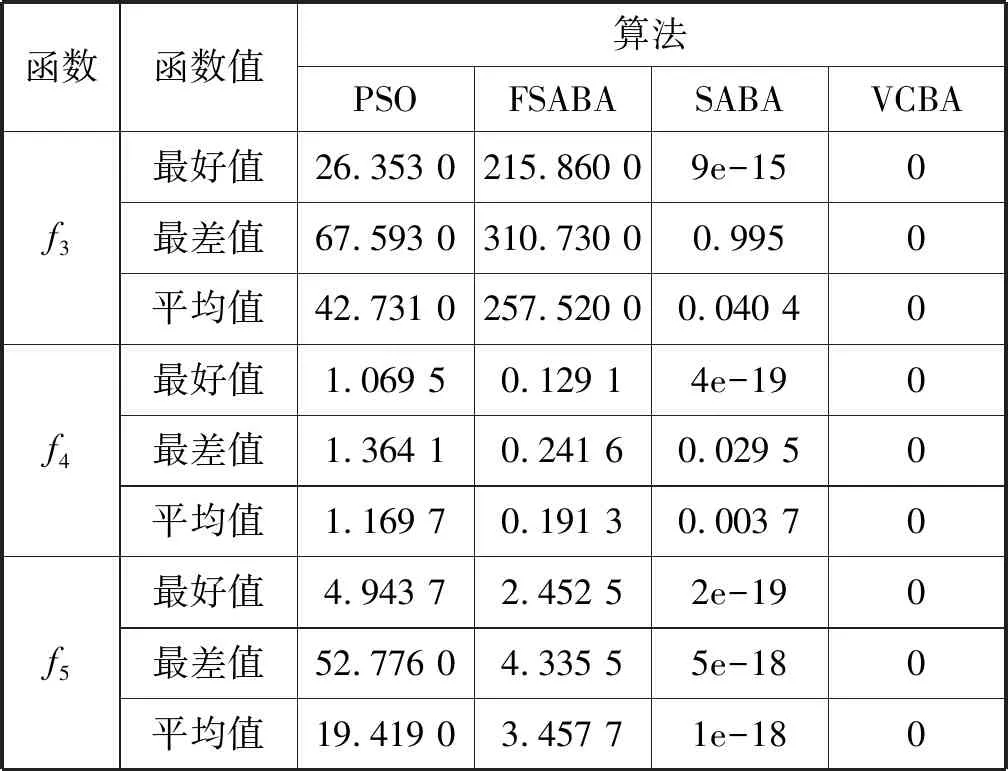
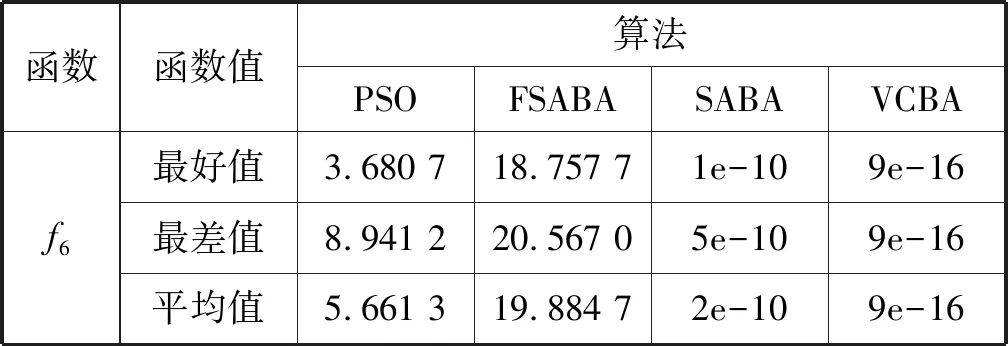
3.3 其他优化算法的寻优结果对比
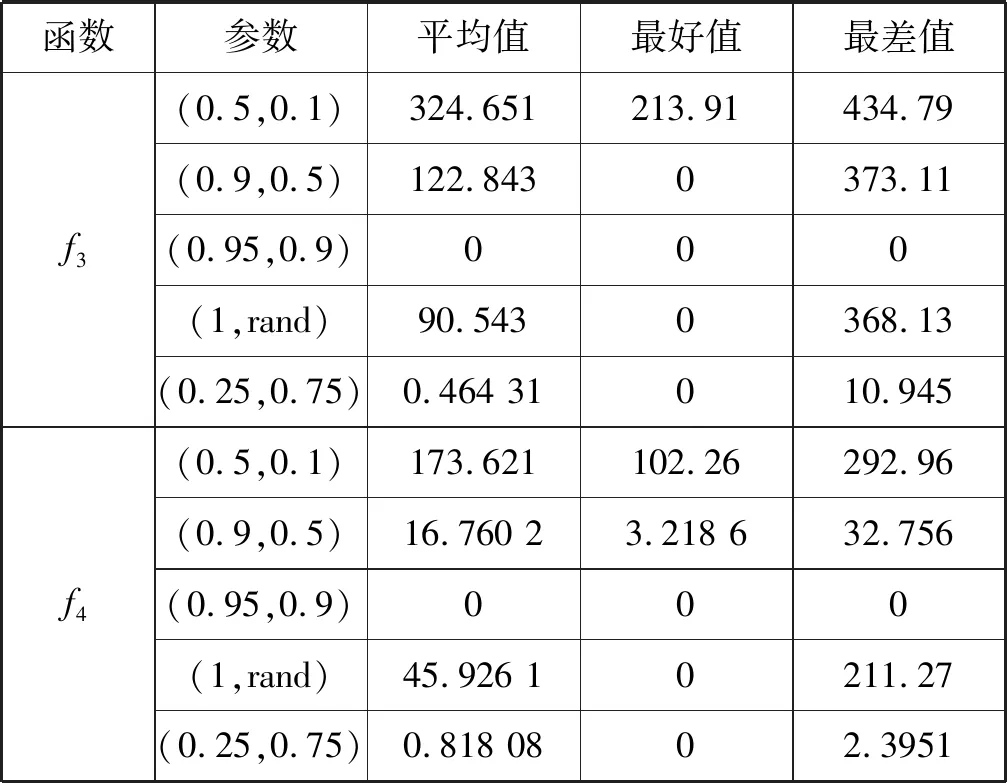
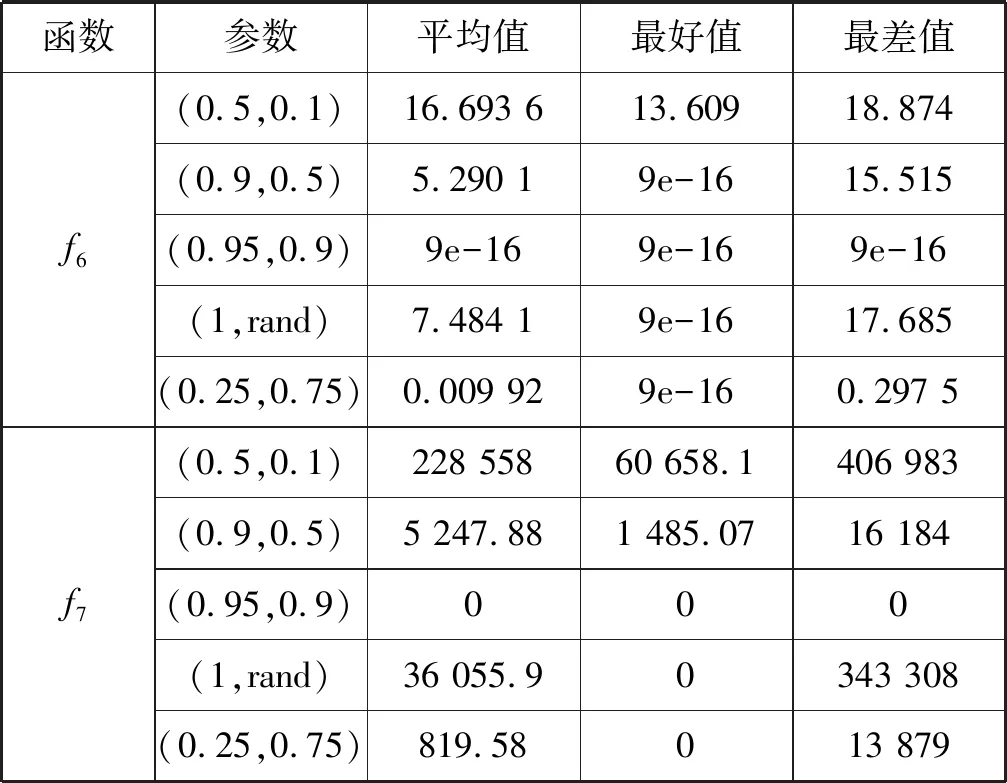
3.4 分析参数对算法的影响
4 结 语

