“数学抽象”素养在高中数学课堂教学中的培养

“数学抽象”素养在高中数学课堂教学中的培养

——以函数的单调性概念的课堂教学策略为例

陈展潘

（惠阳中山中学 广东 惠州 516000）

【摘要】  高中数学新的课程标准（2017版）提出了高中学生在数学学习中应培养好数学抽象、逻辑推理、数学运算、直观想象、数据分析、数学建模六大核心素養。其中数学抽象在六大核心素养中是最重要的，同时是培养学生数学思维能力最重要的一环。因此在平时的数学课堂教学活动中，注重数学抽象能力的培养，有利于学生养成一般性思考问题的习惯，有利于学生更好地理解数学概念，有利于学生对知识的理解和掌握，有利于提高学生的数学成绩。

【关键词】  核心素养 培养 单调性 课堂教学 数学抽象

【中图分类号】  G633.6                      【文献标识码】  A 【文章编号】  1992-7711（2020）04-155-02

一、数学抽象的内涵及其相关概念

通俗地讲数学抽象是通过观察、分析，撇开数学对象的外部的、偶然的、非数学的（物理的、化学的、社会的）东西，分析与提炼出其本质、内在、必然的东西，从空间形式和数量关系上揭示数学对象的本质和规律的一种数学研究方法。数学抽象素养是通过对具体而生动的数学问题进行分析与提炼，概括出一般结论，并应用于解决新的问题之中来体现。数学抽象反映了数学的本质特征，是数学六大核心素养的核心，贯穿于数学教学的全过程。从内容上看，数学抽象包括数学概念、命题、方法和体系的抽象。

二、数学抽象的培养在高中数学课堂教学的现状

在高考成绩的压力下，很多教师为了追求学生成绩，放弃了很多概念的教学，过分的强调解题技巧、方法和解题的步骤，再进行强化式的训练也就是题海战术，这就造成学生会解题、能得分但不知道知识的产生、发展过程。学生对概念课的学习不感兴趣，认为考试不考，课堂枯燥，只要能做题就行了，这就造成学生数学抽象能力难于形成。

三、以函数的单调性概念的课堂教学策略为例谈培养学生的数学抽象能力

（一）教材地位与作用

《函数的单调性》是人教版必修一第1.3节的内容，本节教学内容含单调性的概念、单调性的判断及证明。是学生在初中学习了自变量与函数值变化关系的基础上对函数的更深层次理解，也是函数概念和函数图像学习的延续，函数的单调性是函数的重要性质，是研究函数的重要手段和工具，对以后函数的最值、基本初等函数、导数等知识的教学具有重要的作用。由于它还是初等数学和高等数学衔接的枢纽，所以在本学科具有不可替代的地位和作用，是本学科的核心内容。

（二）教学过程分析

1.创设情景，引入新课

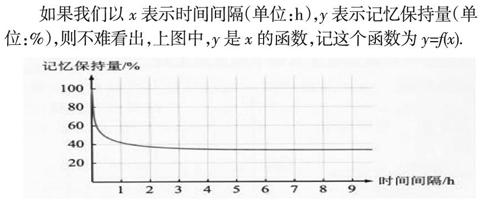
活动一：我们知道，“记忆”在我们的学习过程中扮演着非常重要的角色，因此有关记忆的规律一直都是人们研究的课题.德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究，并给出了类似下图所示的记忆规律。

如果我们以x表示时间间隔（单位：h），y表示记忆保持量（单位：%），则不难看出，上图中，y是x的函数，记这个函数为y=f（x）.

问题1：这个函数反映出记忆具有什么规律？你能从中得到什么启发？

设计意图从学生熟悉的生活实际出发，激发学习兴趣和求知欲望。

活动二：阅读教材，并回答“思考”问题画出下列函数的图象，观察其变化规律：

1. f（x）=x

①从左至右图象上升还是下降__________________  ？

②在区间           上，随着x的增大，f（x）的值随着__________________.

③若x1

2. f（x）=-2x+1

从左至右图象上升还是下降______________________________ ？

在区间                上，随着x的增大，f（x）的值随着_________________ .

③若x1

3. f（x）=x2

①在区间_________________上，f（x）的值随着x的增大而减少，此时若x1

②在区间_________________上，f（x）的值随着x的增大而增大。此时若x1

设计意图：从学生现有知识出发来研究新问题，尊重学生的认知的规律。从最简单的一次函数和二次函数出发，避免了学生对新知识的恐惧和怕难的心理，有利于学生归纳总结出增、减函数的概念，培养学生的数学抽象能力。

2.抽象新知，经历过程

活动三：通过前面的分析得到单调函数的概念：函数单调性定义

知识点1.增函数

一般地，设函数f=f（x）的定义域为，如果对于定义域内的某个区间D内的任意两个自变量x1，x2，当x1

知识点2. 减函数

一般地，设函数y=f（x）的定义域为，如果对于定义域内的某个区间D内的任意两个自变量x1，x2，当x1f（x2），那么就说f（x）在区间D上单调递减，特别地，当函数在它的定义域内单调递减时，称它是减函數。

设计意图：从特殊到一般，学生数学抽象得到提升，形成基本概念。

知识点3.函数的单调性定义

如果函数y=f（x）在某个区间上是增函数或是减函数，那么就说函数y=f（x）在这一区间具有（严格的）单调性，区间D叫做y=f（x）的单调区间。

设计意图培养学生的类比能力，体现数学的联系与变通，再次强化数学抽象能力。

几点说明：

（1）函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质;

（2）从数的角度叙述增减函数：必须是对于区间D内的任意两个自变量x1，x2

①x1）为增函数（减函数）

②函f（x）为增（减）函数，f（x1）>f（x2）（<），则x1>x2（<）

③函数f（x）为增（减）函数，x1f（x2）（<）

（3）从形的角度叙述增减性：

设计意图：从文字、式子、图形三个方面结合，帮助学生理解函数单调的概念，培养了学生的直观想象、数学抽象和逻辑推理的能力，更有利于学生对函数单调性概念的理解。

活动四：例题教学

例1画出下列函数的图象，结合图象说出函数的单调性。

1. y=x2+2x-1     2. y=

例2证明函数f（x）=x+在是单调减函数。

设计意图：由一般到特殊，把抽象数学应用到具体的习题中，更好地理解概念，同时培养了学生的逻辑推理能力，学会用数学思维思考问题，不等式应用也得到了具体体现。

活动五：巩固训练

证明函数y=x+在（-1，0）上为减函数。

设计意图：再次强化训练，体现逻辑推理和数学运算能力。

（三）教学反思

函数的单调性的概念是高中数学概论教学中的一个难点，也是高中学生学习函数的第一个性质，由于抽象能力较差，所以学生对概念的形成存在一定的困难，本节课从生活实际例子出发，再从学生最熟悉的一次函数和二次函数等特殊情况来研究函数单调性，最后探究、抽象出函数单调性的概念。让学生感受到数学来源以生活，避免了学生课堂傻傻的听，课下泛泛的补的不良习惯。体现了数学教学应让学生经历完整的抽象过程、参与完整的抽象活动。真正体现了数学课堂教学应再现抽象的过程，强化抽象的过程。通过课堂教学、学生作业反馈情况说明本节课程较好地完成了教学任务，达成教学目标。

四、“数学抽象”素养在课堂教学中培养的建议

1.教师应严格执行新的课程标准（2017版），在平时的教学活动中不断思考如何进行“数学抽象”素养的培养。

2.学生能力的形成有一个过程，教师应重视这个过程。教学中应该让学生获得数学概念和规律，提出数学命题和模型，形成数学方法与思想，认识数学结构和体系。

3.学生应该强化观察、直观感知的习惯，锻炼实际动手操作的能力，养成对某一类问题的归纳总结的习惯，增强对问题、现象敢于质疑的习惯，为抽象思维培养创造所需条件。避免只会解题而不知其所然。

总之，数学抽象是六大核心素养中最重要的，对学生的发展起有极其重要的作用，在新的高考模式下，课堂教学应加强数学抽象素养的养成，不断提高学生的抽象能力和水平。

[ 参  考  文  献 ]

[1]陶虹萍.探讨高中数学概念教学中核心素养培养策略[J].课程教育研究，2019（45）：130.

[2]罗梦玮，赵继源.数学抽象能力发展过程及培养策略探究[J].南宁师范大学学报（自然科学版），2019，36（03）：137-143.

[3]张金良.解密数学抽象探索教学策略[J].数学通报，2019，58（08）：23-26+66.

[4]刘洪忠.数学抽象素养的培养在高中课堂教学中的体现[J].延边教育学院学报，2019，33（04）：162-164.

[5]孙宏安.数学课程目标刍议——学习《普通高中数学课程标准（2017年版）》[J].中学数学教学参考，2019（22）：2-6+30.