2RPU/UPR+RP五自由度混联机器人参数标定研究
许允斗,王 超,赵春霖,杨 帆,姚建涛,赵永生*
(1.燕山大学 河北省并联机器人与机电系统实验室,河北 秦皇岛 066004;2.燕山大学 先进锻压成型技术与科学教育部重点实验室,河北 秦皇岛 066004)
1 引 言
相较于并联机构的工作空间小、调姿能力差等特点,混联机器人[1-2]综合了串联机器人与并联机器人的特点,具有工作空间大、调姿能力强、刚度高等优点。
目前世界上已得到成功应用的几款混联机器人均来自于国外,包括瑞典的Neos Robotics公司开发的Tricept[3]五自由度混联机器人,德国DS-Technoligie公司研制的Ecospeed-Sprint Z3加工中心[4],以及瑞典Exechon公司研制的Exechon混联加工中心[5-6],它们已成功应用于航空结构件的铣削和冲压模具制作等方面。
国内学者同样进行了五自由度混联机器人的研究,包括天津大学研制的TriVariant混联机器人以及最新提出的Trimule混联机器人[7],清华大学与齐齐哈尔第二机床厂于2003年联合研制的大型龙门式五轴联动混联机器人XNZD2415,清华大学与江东机床联合研发制造的XNZ2010型混联机器人,浙江理工大学研制的2UPR/RPU+RR结构混联机器人[8]等,但我国研发的混联机器人仍停留在实验研究阶段。本课题组基于2RPU/UPR并联机构提出了一种完全具有连续转轴的过约束五自由度混联机器人[9-10]。
目前,关于并联机器人、串联机器人标定算法的研究较多,例如Neagoe[11]提出了一种通用标定算法来进行对串联机械臂的标定。Gattringer[12]提出了一种低成本的工业机器人几何标定策略,并使用激光干涉仪和工业摄像机进行标定。Khalil[13]通过经纬仪辨识出串联机器人的几何参数。Nubiola[14]提出了6D测量系统用来测量工业6轴机器人,提高了机器人的绝对精度,戴智武[15]提出一种采用粒子群算法对Delta并联机器人的误差参数进行辨识的方法,省去了测量坐标系与机器人坐标系的转换。潘伯钊[16]提出了通过激光跟踪仪研究混联机器人标定。本文以本课题组提出的2RPU/UPR+RP五自由度混联机器人为对象,结合机器人自身的结构特征,建立其标定原理与算法,采用激光跟踪仪搭建标定实验平台进行标定实验研究。
2 运动原理与误差分析
2.1 运动原理
本文所研究的混联机器人是在两转一移并联机构2RPU/UPR基础上构造的[17-18],在并联机构动平台上串接一单自由度摇摆头,并在其下方单独安装一单自由度移动平台,如图1所示。
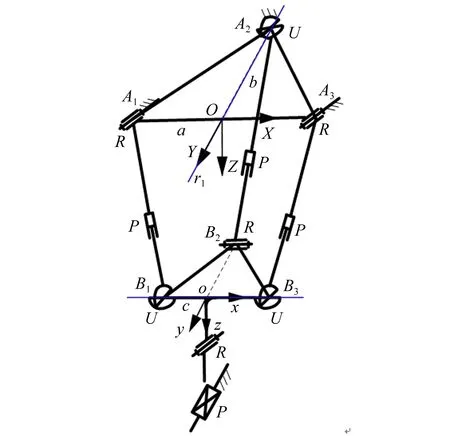
图1 混联机器人的机构简图
文献[9]和文献[19]已经对该混联机器人机构的位置正反解进行了详细分析,但是由于实际加工与装配的需求,样机的安装尺寸与原来的理论模型存在微小的差别。这里主要考虑该差别后,对位置反解模型进行解释。
由于该混联机器人机构所有转轴均是连续的,所以可以等效为如图2所示的五自由度串联机器人机构。这里与原来理论模型的差别在于:摇摆头轴线(z3轴)与,转动副R2轴线和R3轴线的公垂线之间存在偏距l3(理论上为0),考虑该偏距后,等效串联机构的反解解析模型如下:
(1)
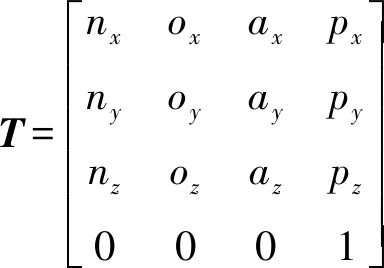
再将θ1,d1和θ2值带入并联机构的反解计算公式可得三个直线驱动支链的输入分别为qi=|Bi-Ai|-qi0,(i=1,2,3)。

图2 混联机器人等效的RPRR+P串联机器人模型
2.2 误差分析
机器人误差的主要来源为几何误差,即在机器人的制造与装配过程中,由于误操作或者加工装配的精度低,致使机器人的关节轴线的位置和各关节轴线之间的相对位姿关系产生误差。一般办法是通过提高加工与装配的精度来尽量避免这样的几何误差,但是由于数控加工机床本身加工精度以及不可避免地人工操作误差,这种方法显然不能完全避免这样地误差。所以,需要通过参数补偿地方法来提高混联机器人的精度,即首先找出关键的几何误差参数,然后通过运动学标定方法辨识出参数实际值,并将其代入到理论模型中进行补偿。
并联机构部分的几何误差来包括连接动、定平台铰点中心的位置误差,具体为定平台上的铰点Ai的位置误差(ΔxAiΔyAiΔzAi)T,动平台上的铰点Bi的位置误差(ΔxBiΔyBiΔzBi)T,以及始状态下各分支的初始杆长误差,但是独立的误差项仅为18项,因为杆长误差与两点位置误差之间存在一个相关项。
由于下方独立的移动平台设计技术较为成熟,精度很高,因此这里不需要进行参数标定。所以串联部分只需考虑摇摆头部分,这部分误差包括连杆长度l1、摆头长度l2和轴线偏置l3的误差Δl1,Δl2和Δl3,以及单自由度摆头的初始角度误差Δθ30。故串联分支共有4个独立的几何误差项。
综上所述,混联机器人的几何误差项共有25项,其中相互独立的几何误差项共有22项。其中杆长误差Δqi与摆头误差Δθ30由于装配过程中跟驱动器零位相关,容易产生较大误差。而其他几何误差仅与加工制造以及装配的精度相关,误差相对较小。故对混联机器人进行误差补偿时,首先要考虑的就是杆长误差Δqi与摇摆头误差Δθ30的标定辨识。对仅对初始杆长值qi0和摆头初始摆角θ30进行的标定我们称之为零点标定,这对机器人精度的提供至关重要。然后对剩下几何误差参数以及零点标定完的初始杆长值和摆头初始摆角的标定,此次标定也称为全标定。各误差参数的理论值如表1所示。
表1 误差参数理论值
Tab.1 Theoretical value of error parameters (mm)
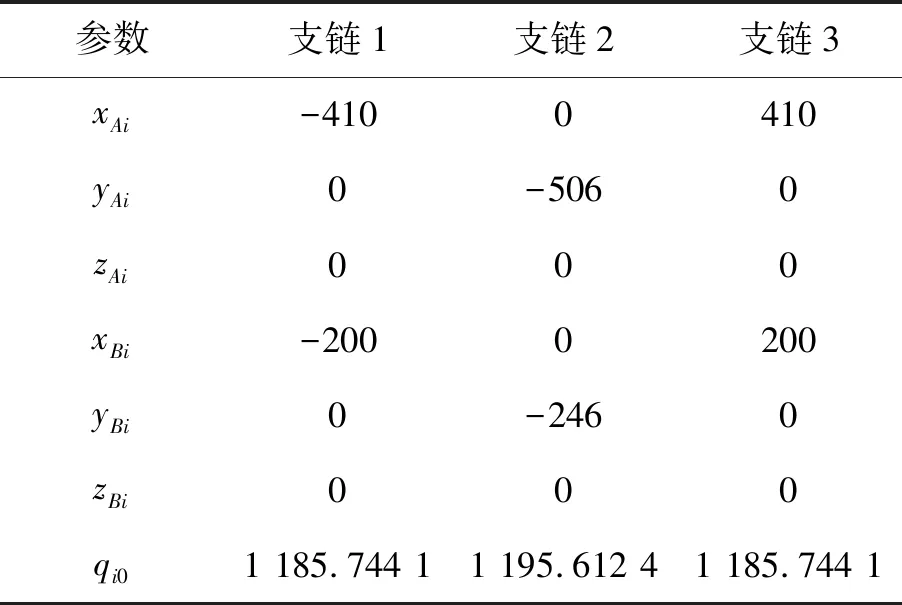
参数支链1支链2支链3xAi-4100410yAi0-5060zAi000xBi-2000200yBi0-2460zBi000qi01 185.744 11 195.612 41 185.744 1
3 标定原理与实验研究
3.1 标定原理分析
这里混联机器人的2RPU/UPR并联机构与单自由度摆头分别进行标定。
3.1.1 并联部分标定
(1) 零点标定原理与算法
根据并联机构部分反解可得:
qi=|RgBi+P-GAi|,(i=1,2,3),
(2)
其中:R表示并联机构动平台坐标系{g}相对于参考坐标系{G}的旋转变换矩阵,P表示平移向量。
当并联机构的姿态发生改变时,3条支链的长度均会发生改变。每改变一次姿态,通过伺服系统可以读取电机的转动的圈数,根据传动比可以计算出支链运动的变化量。那么各分支的杆长为:
qi=qi0+Δqij,
(3)
其中:qi0表示带有误差的3条支链初始杆长,Δqij表示在变换第j个位姿时,第i个支链杆长的改变量。
由式(2)和式(3)可得:
qi0+Δqij=|RjgBi+Pj-GBi|,(i=1,2,3),
(4)
其中:Rj为第j次改变位姿时的姿态矩阵,Pj为第j次改变位姿时的平移向量,可以通过外部高精度测量元件测量。
在研究零点位置误差时,只考虑初始杆长误差共有3个未知数,那么只需要改变1次位姿就可以根据式(4)构造出3个相互独立的方程,我们不妨设:
fij=fij(qi0)=

(5)
其中fij表示动平台处于第j个位姿第i个支链所构造的函数。理论上只需要动平台变换1次姿态即可求出3条支链初始杆长,但是由于测量过程中的可能误操作,测量一次显然不能满足精度的要求,所以需要进行多次测量,综合n次的测量结果才能使最终得到的结果更加逼近实际杆长。构造的方程组为:
(6)
因此求解零点位置误差的问题转化成了求解参数qi0使得目标函数F的值最小的区域寻优问题。其中:
(7)
式中ki为式(7)中各方程所占的比重,由于各分支相互独立,且各方程的对目标函数的影响相同,所以将ki的值设为1。
综上所述,2RPU/UPR并联机构零点位置误差标定问题可以转化为函数最优值问题。
(2) 全标定原理与算法
同样由式(4)可知,每变换一次位姿,可构造3个方程,而全标定共有18个独立参数需要辨识,因为初始杆长可由支链与动定平台连接两点的距离求得,所以至少需要变换6次位姿,但是为了提高识别精度,这里还是变换n次位姿(n>6),构造的方程组如下所示。
(8)
全误差标定时18个独立误差参数的辨识同样也可以转化成式(7)目标函数的优化问题。
3.1.2 摇摆头部分标定
(1)零点标定原理
由于单自由度摇摆头摆角可以通过测量摆头平面相对于动平台平面的夹角直接得到,其中动平台平面A和摆头侧面B均为光滑加工面,如图3所示,所以这里只需要通过测量平面A和平面B的夹角,就可以对摆头初始摆角直接进行补偿。
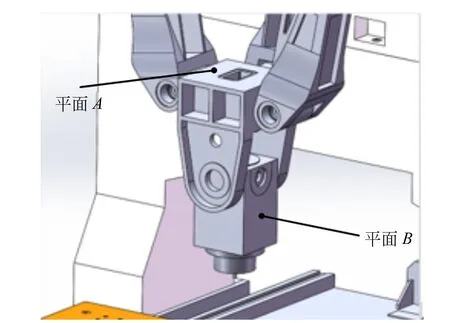
图3 待测量平面A和平面B
(2)全标定原理与算法
因为连杆长度和轴线偏置都是针对的关节轴线之间的相对位置关系,所以这里的标定算法还是通过测量的方法将关节轴线直接测量出来,分别为等效串联机构中z3轴、z4轴和z5轴,然后求解轴线之间的公垂线长度即为这些参数的实际值。这里通过激光跟踪仪采集多组连杆运动轨迹,进而拟合出机器人关节轴线。
3.2 标定系统搭建与标定实验研究
3.2.1 基于激光跟踪仪的位姿测量原理
由激光跟踪仪搭建的标定实验平台如图4所示。

图4 基于激光跟踪仪标定实验平台
图5所示为基于激光跟踪仪的位姿测量原理。激光跟踪仪作为外部测量元件,其可以精确的测量出跟踪仪(绝对)坐标系下目标点的三维信息,并可以通过特征点建立起坐标系。
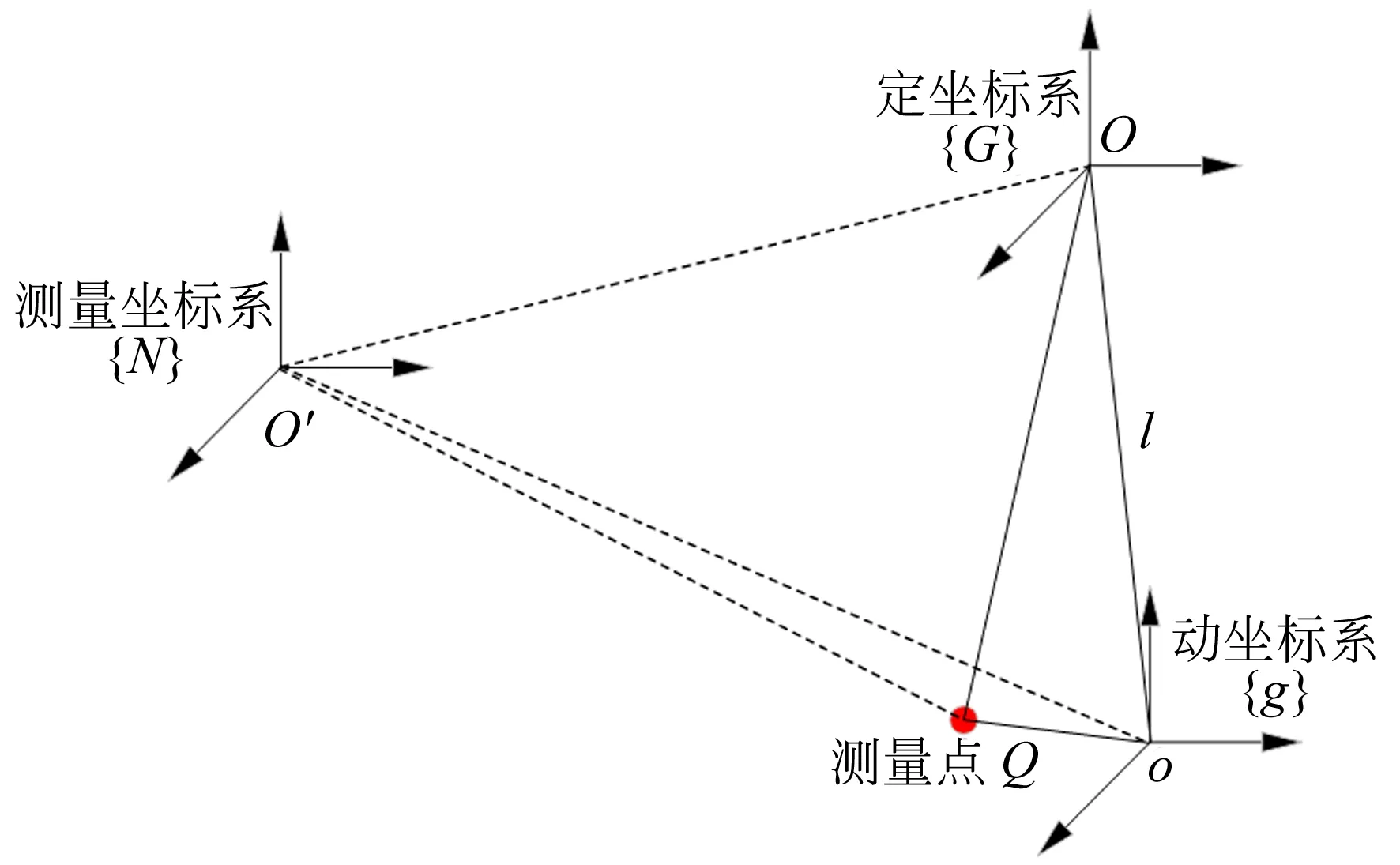
图5 激光跟踪仪的位姿测量原理
通过外部测量传感器建立测量坐标系{N},定坐标系{G}以及动坐标系{g}。当动平台开始运动时,动坐标系的位置与姿态的测量就变得十分困难,故引入一个辅助点来进行间接测量,设Q点为动平台上一个已知测量点。通过驱动数控系统改变并联机器人的杆长,从而改变动平台相对于定平台的位姿。
其中l表示定坐标系{G}原点O到动坐标系{g}原点o的矢量,于是,根据图5可以得到:
l=GOQ-GoQ,
(9)
根据刚体位姿的描述,可以得到:
(11)
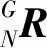
将式(10)和式(11)代入式(9)中整理得:
(12)
根据前面分析可以得知混联机器人并联部分具有三个自由度,并且动平台在运动的过程中没有Y轴方向的耦合位移量,则l可表示为:
(13)
将式(13)代入式(12)中整理得:
(14)

3.2.2 动、定坐标系测量
由上述原理可知,需要测量出混联机器人机构动、定坐标系的原点位置和各坐标轴矢量,根据激光跟踪仪拟合的关节轴线和定平台及动平台法线,在激光跟踪仪软件SA-job中建立坐标系。
(1)动平台动坐标系的建立。通过拟合动平台上的U副近动平台端的轴线,将其作为动坐标系的X轴;再拟合出单自由度摇摆头的轴线,将其作为动坐标系的Y轴的矢量方向;接下来沿着两条直线的公垂线平移单自由度摇摆头的轴线,相交的点作为动坐标系原点,Z轴通过“右手定则”判断。
(2)混联机器人定坐标系的建立。由于定平台铰链无法直接测量,故先通过拟合定平台上两个R副轴线,再做出两R副轴线的中心线,将其作为定坐标系的Y轴;再拟合出工作台平面的垂直向量,将其作为定坐标系的Z轴,X轴通过“右手定则”判断。
(16)
由于定坐标系Y轴是根据左右两R副拟合得到,故A1和A3铰点的实际位置应关于原点对称,即:
(17)
综上,混联机器人标定实验的定坐标系与动坐标系建立完毕。
3.2.3 并联机构部分标定
(1)零点标定
规划混联机器人三根驱动杆以0.3 mm的增量运行,共运行30次,按照图6示意摆放靶球至动平台上表面。测量得到靶球在动坐标系下的坐标为:
gQ=
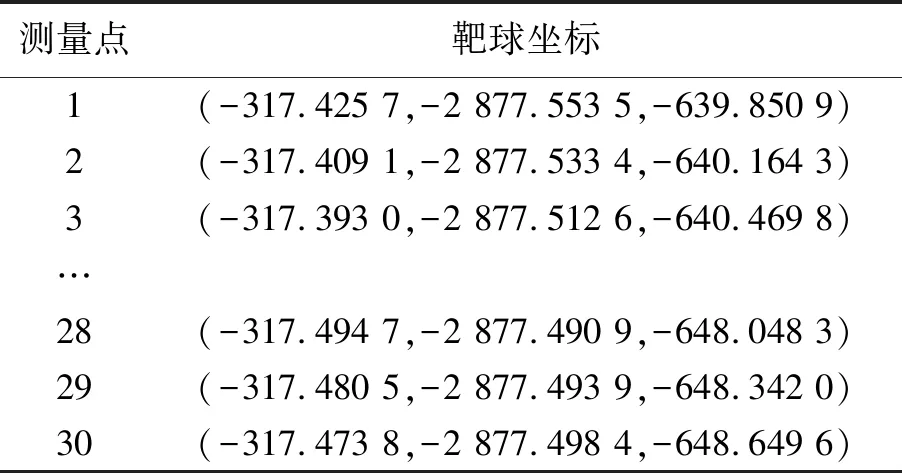
通过数控系统改变混联机器人的驱动杆长的同时,记录出靶球的在激光跟踪仪坐标系下的坐标如表2所示。

图6 靶球摆放示意图
表2 杆长变化时靶球的坐标
Tab.2 Coordinates of target ball with varying rod length
测量点靶球坐标1(-317.425 7,-2 877.553 5,-639.850 9)2(-317.409 1,-2 877.533 4,-640.164 3)3(-317.393 0,-2 877.512 6,-640.469 8)…28(-317.494 7,-2 877.490 9,-648.048 3)29(-317.480 5,-2 877.493 9,-648.342 0)30(-317.473 8,-2 877.498 4,-648.649 6)
将上述数据代入式(14),可以得到每次杆长改变时的θ1,θ2和d值如表3所示。
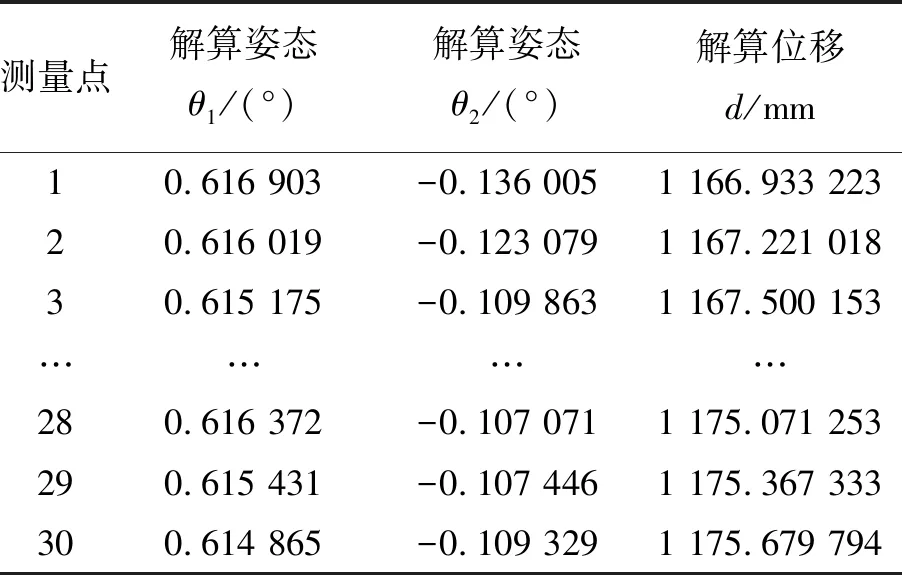
表3 解算得到的θ1,θ2和d值
然后采用求解的最优解,可得零点位置误差辨识的结果,如下表所示。

表4 零点位置误差辨识结果
(2)全标定
同样地,对式(8)求各参数的最优解,全误差辨识结果如表5所示。
3.2.4 摇摆头部分标定
对单自由度摇摆头进行零点位置误差标定时,首先通过数据点拟合出动平台上平面和单自由度摇摆头的侧平面,然后求得两平面的法向量。表6为测量得到的两平面上的点坐标。

表5 全误差辨识结果

表6 测量得到的两平面上的点坐标
由表6拟合出动平台上平面的法向量为(0.014 4,-0.999 8,0.002 1),单自由度摇摆头的侧平面的法向量为(-0.873 8,-0.036 7,-0.013 6),计算出两向量夹角为88.620 11°,故通过数控系统补偿的单自由度摇摆头零点位置误差为Δθ30=1.379 89°。
在进行单自由度摇摆头全误差标定时,需要通过激光跟踪仪拟合出混联机器人的z3轴线、摇摆头转动轴线(z4轴)以及刀具轴线(z5轴),在建立动坐标系时已经拟合出z3轴线和z4轴线,故还需要拟合出刀具轴线,将磁性表座吸到刀轴表面进行测量,如图7为刀具轴线的测量过程。

图7 刀具轴线的测量过程
通过拟合得到的3条轴线的函数表达式如表7所示,计算得到z3轴线与z4轴线公垂线长度l1为255.431 1 mm,z3轴线与z4轴线的公垂线,与刀具轴线的偏距l3为5.018 1 mm。通过测量单自由度摇摆头末端点,得到其与z4轴线间的距离l2为358.061 7 mm。

表7 拟合的三条轴线表达式
4 精度测量
本文主要使用中国国标GBT17421.2-2000的计算测量方式来对五自由度混联机器人进行精度测量[20]。
根据国标规定,数控设备的精度检测需要在设备的工作空间内,沿平行于坐标轴的某一轴线方向选取若干个定位点(5~15个),对于每个点分正负两个方向重复多次定位测量(3~5次),将测到的真实数据点代入国标公式中即可完成对数控设备的精度检验。
使用全世界最大的激光干涉仪生产厂家之一的安捷伦科技公司生产的Agilent(安捷伦)5529A激光干涉仪作为精度测量元件,分辨率为10 nm,该激光干涉仪使用双频激光作为测量激光,有效的减小了空气扰动对测量的影响。具体的精度测量方案如下:
步骤(1):搭建起激光干涉仪测量系统,安装好温度传感器,材料传感器后,将反射镜放置到混联机器人远端,干涉镜放置到待测量目标处,如图8所示。

图8 激光跟踪精度测量系统
步骤(2):调整好激光光路,使得在全工作空间内激光可以反射回干涉仪。
步骤(3):按照图9所示的测量行程路线示意图进行测量数据,表8为各轴的测量参数设置。
为了对比零点位置误差标定和全误差标定对混联机器人的精度影响,分别测量出混联机器人未标定时、完成零点位置误差标定后以及完成全误差标定后,X轴与Z轴的定位精度。由于Y轴输出由独立的单自由度移动平台完成,这里没有给出标定过程,直接测量出其定位精度和重复定位精度为0.015 mm和0.01 mm。表9和表10为X和Z轴的位置精度测量结果。
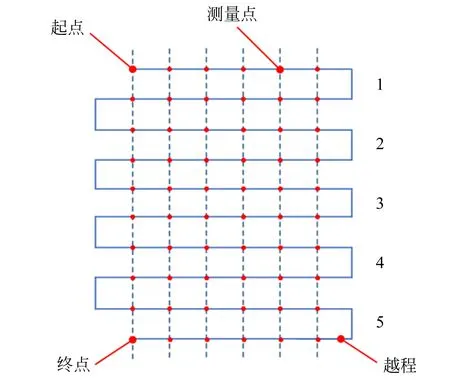
图9 测量行程路线示意图

表8 各轴的测量参数设置
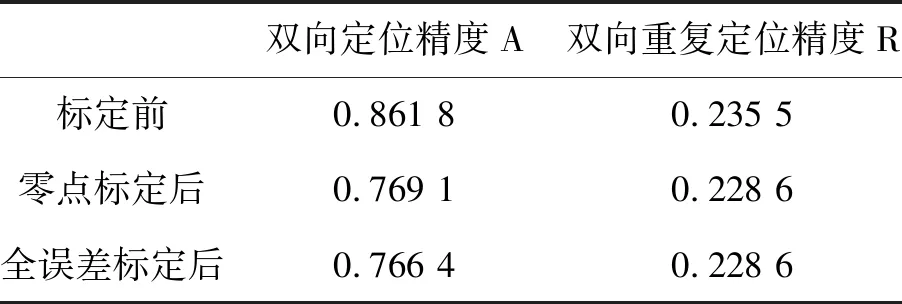
表9 X轴定位精度

表10 Z轴定位精度
5 结果讨论
从实验结果来看,五自由度混联机器人的Y轴定位精度最高,Z轴次之,X轴精度最低。一方面,由于Y轴运动由独立的单自由度移动完成,而Z轴和X轴运动则是4个电机联动完成的。另一方面,从刚度角度分析,混联机器人整体处于悬臂状态,其侧向刚度(X轴方向)要低于轴向刚度(Z轴方向),这也是X轴定位精度较低的主要影响因素。
通过运动学标定,其定位精度和重复定位精度较未标定时均有一定程度的提升,X方向的定位精度提升了近0.1 mm,Z方向的定位精度提升了近0.03 mm。其中零点标定对定位精度的提升比较明显,在零点标定基础上完成的全标定对定位精度有较小幅度的提升。实验数据充分表明了本文所提出运动学标定方法的有效性。
6 结 论
本文针对2RPU/UPR+RP过约束混联机器人的结构特征,分析了其误差源参数,共有22个独立参数需要标定,并将其分为并联机构和单自由度摇摆头两部分,分别建立这两部分的零点标定与全标定方法。提出了基于激光跟踪仪的位姿测量原理,搭建了标定实验平台,得到了误差参数的真实值,计算了标定前后的混联机器人的定位精度,结果表明,零点标定对机器人定位精度的提升非常明显,X轴和Z轴定位精度的分别从0.861 8 mm和0.093 8提升到了0.769 1 mm和0.060 5 mm,在零点标定基础上的全标定对定位精度也有较小程度地提升。
通过标定后,X方向定位精度仍然比较低,分析其主要因为为并联机构在X方向的侧向刚度比较低,主要支链驱动单元的导向部分结构刚度弱引起的,目前正在研讨改进方案,后续将进一步对该混联机器人进行改造。

