圆柱轴线相交相贯线解析性质分析
孙 华
(辽宁轨道交通职业学院,辽宁 沈阳 110023)
轴线相交的两个圆柱立体相贯是工程上较为常见相贯形式,常用的立体相贯线的投影求解方法有两种,图解法和解析法[1-2]。精确图解特殊点是绘制相贯线投影的关键,文章通过对两个圆柱轴线相交时相贯线投影上所有特殊点的解析分析,从而求得了相贯线投影的特殊点的图解方法。
根据两个圆柱轴线相交的角度不同,分为轴线正交和轴线斜交两种情况,如图1 和图2 所示,轴线相交的角度不同,产生的相贯线就不同。
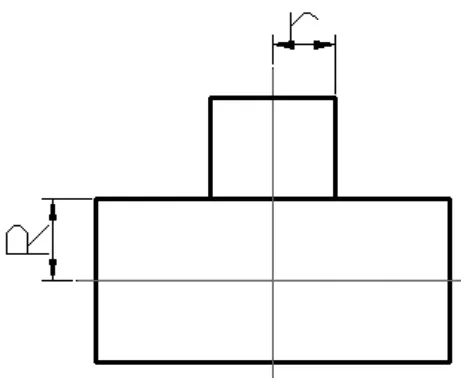
图1 轴线垂直相交圆柱

图2 轴线斜交圆柱
1 解析性质分析
1.1 轴线正交相贯线解析
如图3 所示,在主视图中建立直角坐标系,一个圆柱半径为R,另一个圆柱半径为r,主视图中取AB=X,那么俯视图中,在左视图中,中所以在主视图中的相贯线数学模型为:,最低点即是y'=0,解得x=0,代入得,即最低点坐标E(0,)。当R=r时,,即相贯线是两条线段,最低点坐标P(0,-R)。
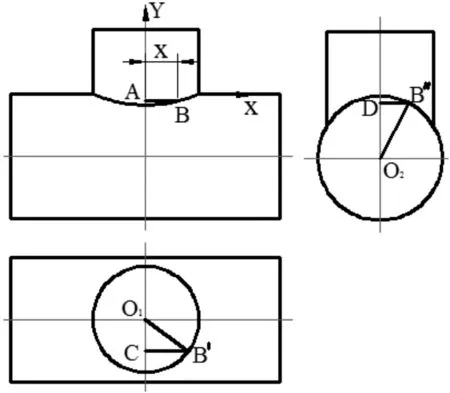
图3 轴线垂直相交圆柱三视图
1.2 轴线斜交相贯线解析
如图2 所示,当两圆柱轴线斜交时,左视图中有:
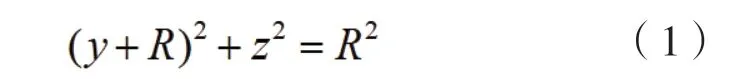
俯视图中,所有的点都是椭圆曲线中的点,所以有:

由式(1),(2)得:

欲求式(3)所表达的方程在Y轴方向极值点(即相贯线的最低点),需根据极值法对其求导。将式(3)表达为隐式

则其极值点[3-4]应该满足:

式(5)为一条直线方程,容易看出这是一条与圆柱半径无关的直线。它既是式(3)具有Y轴方向极值点的条件关系式,也具有特定的几何意义,即相贯线最低点在倾斜圆柱的轴线上。
将式(5)代入到式(3),可得到z=r,将z=r代入到式(1)得,即点是相贯线最低点坐标。
相贯线另外特殊点是与Y轴交点,故将x=0代入到式(3),可得到,即 点W(0,是相贯线与Y轴交点坐标。当R=r时,由式(3)整理得,相贯线是两条线段,最低点坐标V(-Rcotθ,-R)。
2 特殊点图解方法
2.1 轴线正交相贯线图解法
1)等径轴线正交。
2)不等径轴线正交。

图4 等径轴线正交相贯线
①以LJ 的中点I 为圆心,R/2 为半径画半圆;
②以L 为圆心,r为半径,弧交半圆I 于点K;
④用平滑曲线连接点M,E 和N。

图5 不等径轴线正交相贯线
2.2 轴线斜交相贯线图解法
1)等径轴线斜交。

图6 等径轴线斜交相贯线
2)不等径轴线斜交。
图解过程如下:
②过点E 作LI 垂线,交倾斜圆柱轴线于点Q;
③取LT=r,作TP 垂直于MN,垂足为P;
④以点L 为圆心,TP 长为半径作弧,交半圆I于点K。在LJ 上取JU=JK,过U 作LJ 垂线,交倾斜圆柱轴线于点S,取LX=LS,过X 作LJ 垂线交倾斜圆柱轴线于点Y,取LW=LY。
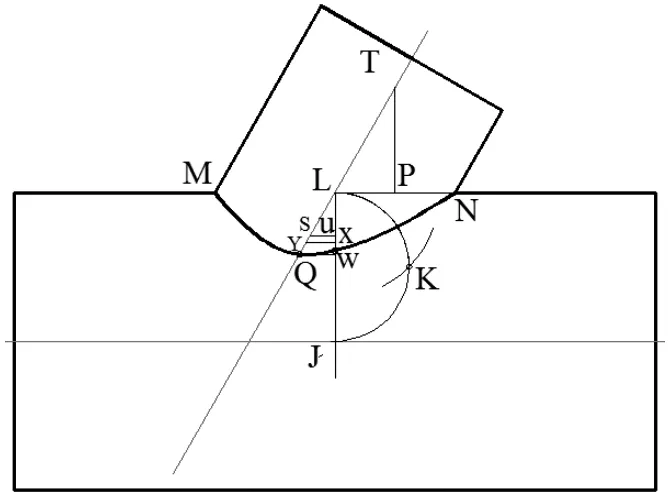
图7 不等径轴线斜交相贯线
3 结论
通过数学解析方法的详细分析,轴线相交的圆柱特殊点的准确位置可以用图解方法确定。
1)轴线相交的两个圆柱相贯线,无论是正交还是斜交,其相贯线投影上最低点的坐标都是在上面圆柱的轴线上,并最低点的竖直方向坐标值都为。
2)两个圆柱轴线无论是正交还是斜交,只要两个圆柱半径相等,相贯线的投影就是由两条线段组成,其余情况相贯线的投影都是曲线。
3)只有两个圆柱轴线正交时,无论半径是相等或者不等,产生的相贯线的投影都是左右对称的;两个圆柱轴线斜交时,如果半径相等,则相贯线左侧线段倾斜程度大,右侧线段倾斜程度小;如果半径不相等,则相贯线左侧曲线弯曲程度大,右侧曲线弯曲程度小。

