基于社会力模型的人员逆流行为
魏欢欢,周 颖,张 磊,鲍东宾
(河北工业大学 人工智能与数据科学学院,天津 300130)
0 引 言
在发生突发事件的情形下,人作为一个独立的个体将会产生恐慌、冲动、随大流等特殊心理[1],从而会产生逆流行为、从众行为、小团体行为[2,3]等。在研究人员疏散方面,行人动力学模型主要有宏观模型[4,5]和微观模型[6,7],人员疏散的研究大都集中在引导疏散上[8-10],其中董书衡从地铁站的特性、人员行为学原理和人员疏散行为特征等出发,收集大量人员基本特征与人员行为反应数据,并分析地铁站的特殊结构、人员基本特性等因素对人员疏散时间的影响;陈庆栋研究高大净空建筑火灾烟气蔓延时空分布对人员安全疏散过程的影响等。
在发生紧急情况的条件下,由于要帮助他人撤离、自身素质较低或者营救弱势群体等原因造成的逆流行为,会造成通道的堵塞,形成人员拥挤,进而发生伤亡事故。目前,对人员疏散过程中逆流行为的研究很少,为解决该问题,本文在基于社会力模型的基础上,首先对出口场馆中的逆流行为进行建模;其次分析多出口场馆中的两种逆流行为情况下对疏散的影响;最后在单出口场馆中研究逆流人数的个数来对所建模型进行验证分析。
1 基于社会力模型疏散仿真模型
在人员疏散的研究领域中,社会力模型作为一种较为典型的微观模型,模型表明,每个人都作用着社会力,即人与人之间、人与障碍物之间及人与周围环境之间的相互作用力,该模型可以很好地模拟个体在疏散过程中的一些行为特征及常见的疏散情况,为后文构建逆流行为模型仿真提供相应的理论基础。
1.1 选择出口模型
根据疏散个体到目标出口的距离、人员密度及人员数量建立个体选择目标出口模型。
(1)视野范围
根据文献[11]可将个体的视野范围(即个体在人群中看其他个体的视野范围)定义如下:在个体i的当前位置O与目标出口位置(Exit)所形成的直线方向上,第L个个体所在的位置为点P,则以点O为圆心,线段OP为轴线,以2α为圆心角,OP为半径的扇形区域即为个体i的视野范围。当L=6时,视野范围如图1所示。
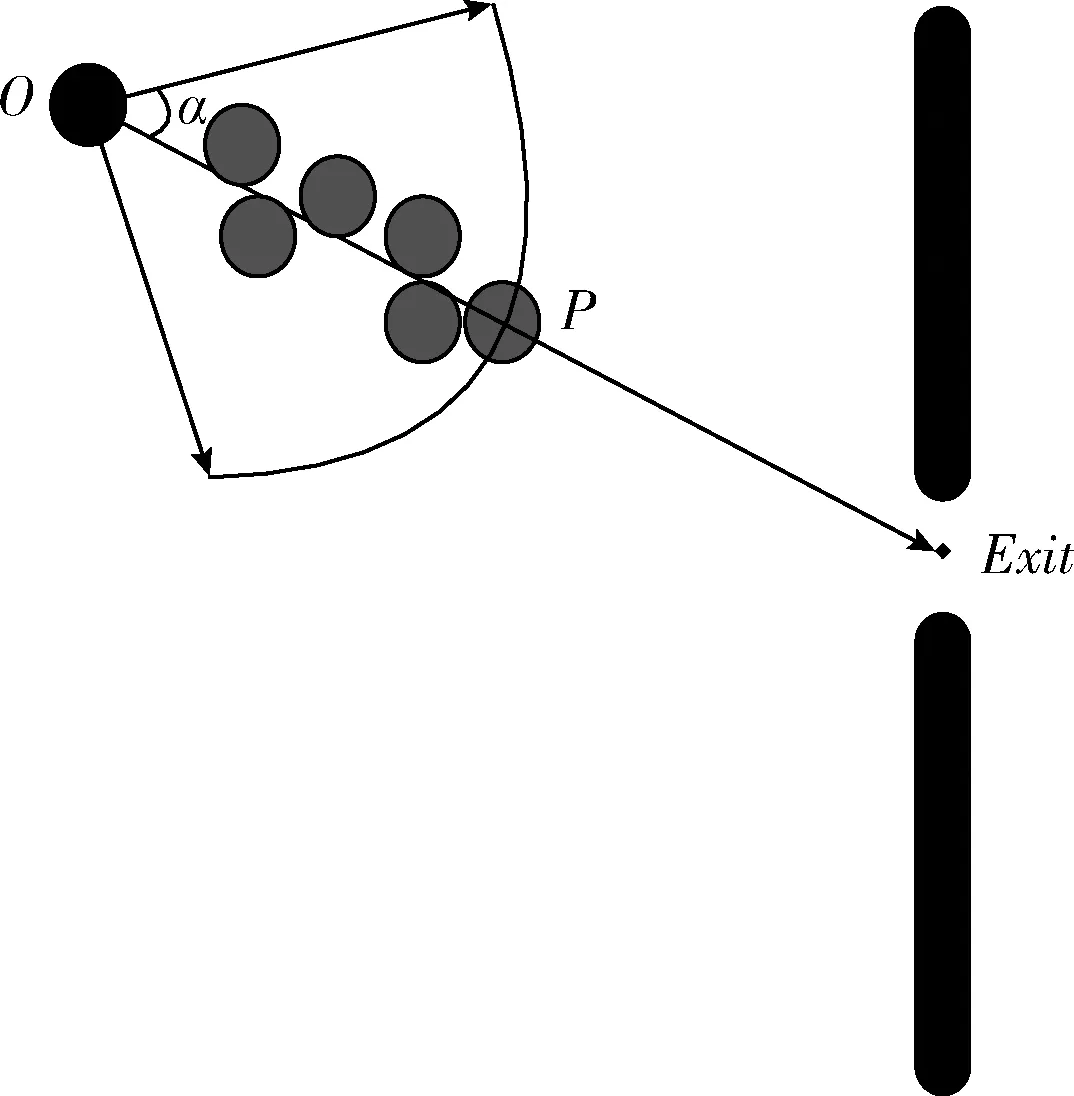
图1 个体的视野范围
(2)出口选择
假设整个场馆中有M个出口,且En表示场馆的第n个出口,n=1,2,3,…,M。 则所确定的出口目标模型为
(1)
其中,μ1,μ2,μ3表示目标出口各因素的权系数,且μ1+μ2+μ3=1,dn表示个体到出口n的距离,pn是该个体在视野范围内的人数,ρpn表示在该视野范围内的人群密度
(2)
(3)
(4)
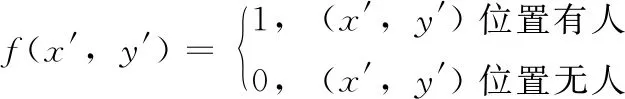
(5)
式中: (xi,yi) 和 (xEn,yEn) 分别表示个体i和出口n的位置坐标,该个体的视野范围半径为R, 视野范围的夹角为2α, 人的半径为r,f(x′,y′) 表示位置坐标在 (x′,y′) (该坐标为个体圆心的坐标,除圆心外的圆内坐标不视为被个体占据的点)上是否有人占据。
1.2 社会力模型描述
1.2.1 模型框架
Helbing等提出社会力模型中,在社会力作用下个体发生相应运动。社会力模型[12]可以比较精确描述个体运动变化过程,此外还可解释在出口处出现堵塞现象的原因。
1.2.2 模型建立
社会力模型是依据牛顿第二定律对个体进行运动建模的,建立个体运动与受力之间的关系。模型中的社会力包括为到达所期望的目的地个体本身的期望力、其他个体对自身的作用力以及墙壁等障碍物对自身产生的作用力,其动力学方程如下
(6)
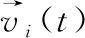
(1)期望力
期望力是个体本身想到达目的地时自身产生的动力,在疏散过程中个体产生速度很大程度上由期望力的大小决定。个体在期望力的作用下向出口方向尽快按照期望的速度行动,如式(7)所示
(7)
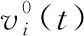
(8)
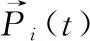
(2)个体之间的作用力
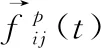
(9)
个体为了防止和他人产生碰撞,会产生一种心理作用力,且这个心理作用力会随着距离的改变而发生改变,当个体之间的距离达到最小时,这种心理作用力最大,如式(10) 所示
(10)
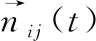
(11)
(12)

但是,在疏散过程中,个体之间的作用力不仅与个体之间的距离大小有关,实际中个体相对于后方的疏散人群而言会主动避让该个体之前的人群。周围的环境包括其他个体或者物对个体的心理作用力影响是不同的,即在个体视野范围之内的个体或物对该个体的心理作用力影响较大,视野之外的人或物影响力较小,也就是人或物相对于该个体的位置对个体的心理作用力影响很大,因此对个体之间的心理作用力进行改进,如式(13)所示
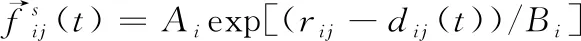
(13)

(14)
其中
(15)
在人群密度较低的场馆中,随着疏散时间的延长,在身体之间就会产生物理作用力,这种作用力包括妨碍个体运动切线方向的滑动摩擦力和个体接触时相互挤压产生的弹力,如式(16)所示
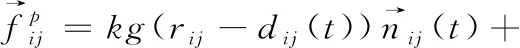
(16)
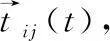
(17)
g(x)与x的函数关系是如式(18)所示
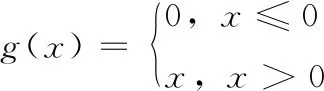
(18)
(3)个体与障碍物或墙壁之间的作用力
在场馆内的人员疏散过程中,随着拥挤程度的加剧,距离会变得越来越小,最后个体与障碍物或墙壁之间会产生物理作用力,如式(19)所示
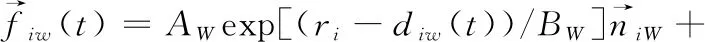
(19)

2 逆流行为模型建立及算法描述
在人员疏散的过程当中,不免有人会在疏散的过程中由于某些原因产生返回行为,这就形成了逆流行为。这些返回的原因有:寻找自己的亲人、返回拿落下的物品、帮助弱势群体撤离等,这样会形成人员移动方向的交叉,很可能发生踩踏事故,产生严重后果。存在逆流行为的人群中包括逆流个体和非逆流个体,其中逆流个体包括不返回个体和返回个体,本文中将逆流个体中的不返回个体定义为主个体,将逆流个体中的返回个体定义为从个体,下文与此相同。例如在出口附近的从个体回到场馆中寻找自己的亲朋好友(即从个体)。
根据从个体在靠近主个体之前主个体的状态,将常见的逆流行为归纳为:主不原地等待逆流行为和主原地等待逆流行为。主不原地等待逆流行为是指主个体不会等着从个体靠近后才向出口移动,而是自身主动向出口移动;主原地等待逆流行为是指从个体在未靠近主个体时,主个体会在原地等待从个体的靠近,待从个体靠近后两者一同向出口移动。
2.1 主不原地等待模型描述及建立
2.1.1 主不原地等待决策模型描述
在存在主不原地等待逆流行为的人群中包括逆流个体和非逆流个体,其中逆流个体包括主个体和从个体。非逆流个体的决策模型与疏散人群中的普通个体决策模型一致,逆流行为中的决策模型包括返回个体和非返回个体的决策模型,而返回个体的决策模型主要体现了从个体的行动方向以及主从个体之间的吸引力。其机理图如图2所示。
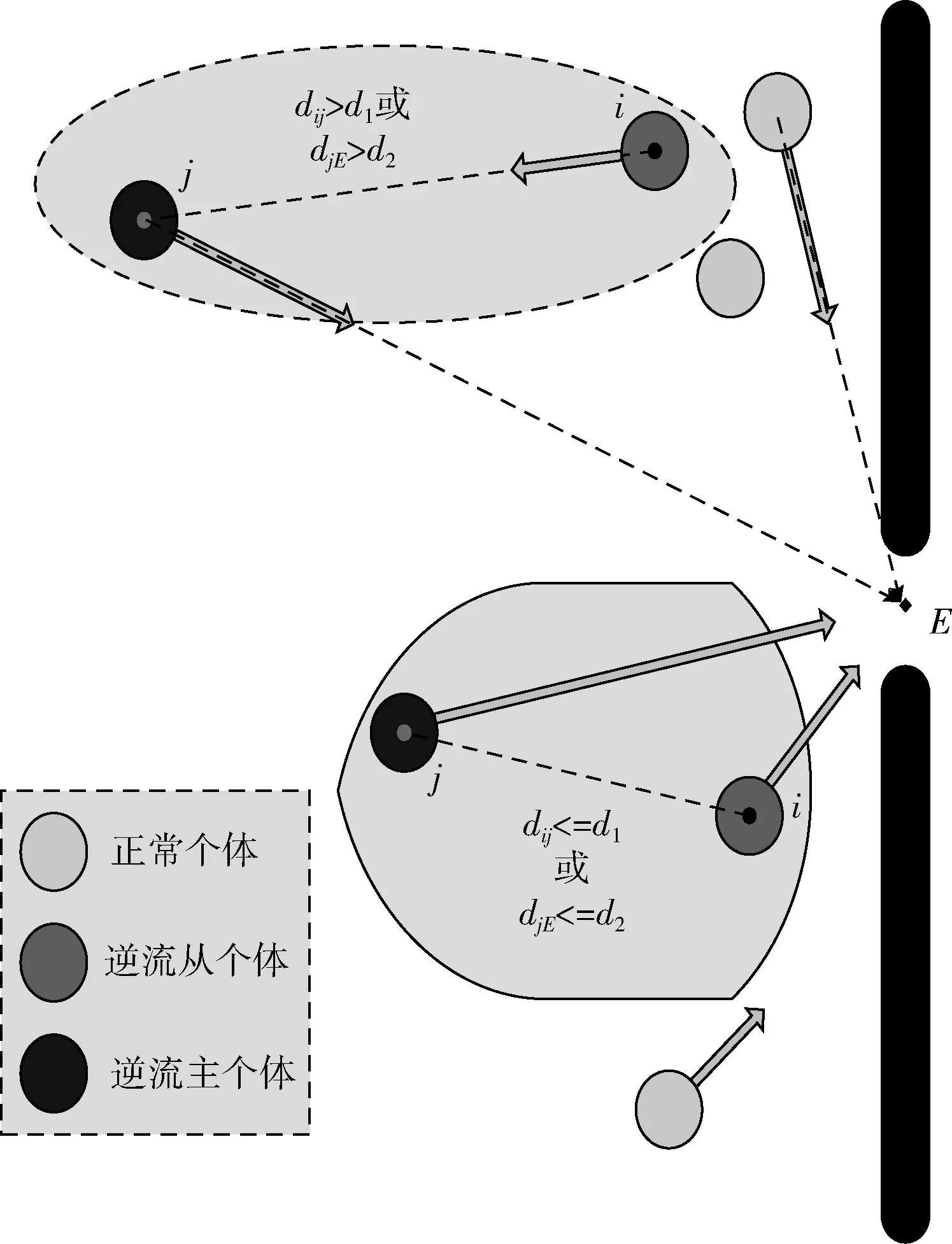
图2 主不原地等待机理图
2.1.2 主不原地等待决策模型建立
(1)主个体决策模型
在疏散过程中,主个体的期望目标是出口,根据主从间的距离、期望力大小来确定自身行动方向。同所述的非逆流个体的目标及行动方向的决策相同,不再叙述。该模型中逆流行为的主个体按照自己的意愿向出口进行疏散。
(2)从个体决策模型
当从个体还没有靠近主个体时,需返回,此时从个体的期望方向是主个体,即此时式(8)中,个体的期望目标位置为个体j。 同时从个体还受到主个体的吸引力如式(20) 所示
(20)
其它力与社会力模型相同,在此不再赘述。
从个体会根据自身距离主个体的距离来决定自己的方向,当从个体距离主个体较远时,从个体会先向主个体靠拢,然后一块向出口移动;当主个体距离出口较近时,从个体向出口移动;当主从个体距离较近时,两者均按照均朝出口进行疏散。对于逆流行为中的从个体下一步的移动目标方向如式(21)所示,其中公式中的d1,d2是参数
(21)
ri,rj分别表示从个体和主个体此刻的位置,dij(t) 表示在t时刻主从个体之间的相对距离,djE(t),diE(t) 分别表示主个体和从个体各自到出口的距离,本文如不做特殊声明,下同。
当主从个体靠拢后与主个体的决策模型相同,并一同向出口方向行动,在此不再赘述。
2.2 主原地等待模型描述及建立
2.2.1 主原地等待决策模型描述
在该模型中逆流行为的主个体当从个体未靠近时,主个体原地等待;从个体向等待个体方向移动,向主个体靠拢。等从个体向主个体达到靠拢后,一同向出口进行移动进行人员疏散。其机理图如图3所示。
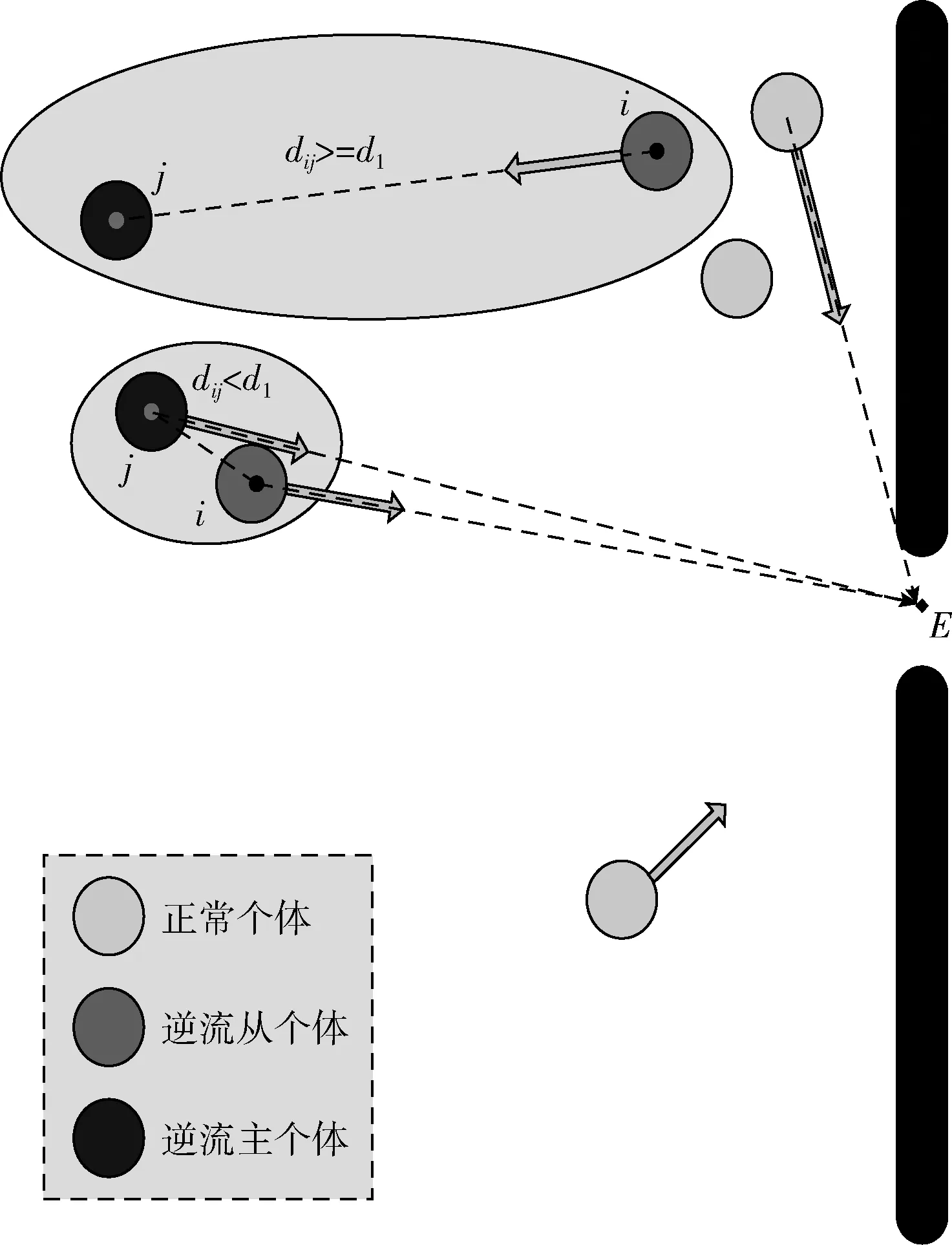
图3 主原地等待机理图
2.2.2 主原地等待决策模型建立
(1)主个体方向决策模型
在人员疏散的过程中,主个体会在从个体靠近的过程当中先原地等待;等从个体靠拢后主从个体均向门口移动。在逆流过程中,主个体的下一步移动方向如式(22)所示
(22)
其中,rE,rj分别表示出口以及个体j的位置坐标,dij(t) 和djE(t) 分别表示个体i和j的距离以及个体j到出口的距离。
(2)从个体方向决策模型
当从个体距离主个体较远时,从个体会先向主个体靠拢,即此时式(8)中,个体的期望目标位置为个体j。 达到靠拢后和主个体一同向出口方向移动,在逆流过程中,主个体的下一步移动方向如式(23)所示
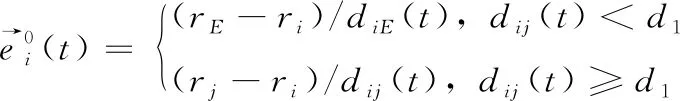
(23)
此外个体j对个体i有吸引力作用,如式(20)所示,该模型其它受力同社会力模型相同,在此不再赘述。
3 仿真结果及分析
本实验用Visual Studio 2017对场馆中的人群疏散行为进行仿真,其中浅灰色圆点代表普通人群,中灰色圆点代表逆流人群的从个体,黑色代表逆流人群中的主个体。
3.1 本次仿真场景
(1)房间大小为15 m*15 m,墙宽为0.25 m;
(2)房间设置2个出口,出口宽度为1 m;
(3)在该房间内随机布置共200名疏散人员,且男女比例1∶1;
(4)存在逆流,逆流主从个体各为4。
3.2 参数取值
在本文的实验模型中,相应的参数取值如下:AE=1500 N/m,BE=0.08 m,Ai=1500 N/m,Bi=0.08 m,d1=0.5 m,d2=1.5 m,Aj=1500 N/m,Bj=0.08 m,Aw=1500 N/m,k=0.9×105kg/s2,τi=0.5 s,κ=1.8×105kg/s2,λ1=0.75。出口选择的相关参数见表1。

表1 出口选择参数
3.3 无逆流(情景1)
以上4个图为仿真过程中的4个时刻仿真状态,其中图4(a)为初始状态。由图4可以看到,在不存在逆流的情况下,待疏散的人员自主的向出口进行疏散,并在出口附近形成拱形或者半圆形;可以观察到堵塞现象,随着堵塞行为的发生,变得越来越拥堵。

图4 无逆流
3.4 主不原地等待逆流(情景2)
从图5可以看出,在存在逆流且是主不原地等待情况下,在疏散过程中,非逆流个体均朝出口进行移动,并且形成拱形或半圆形;逆流的主个体也向出口进行移动,逆流的从个体向远离出口的方向移动,远离出口,存在明显的逆流行为;当逆流从个体靠近主个体后会同主个体一同向出口移动;当逆流从个体意识到自身和主个体都靠近出口时,逆流的从个体也会向出口移动。

图5 主不原地等待逆流

图6 主原地等待逆流
3.5 主原地等待逆流(情景3)
从图6可以看出,在存在逆流且是主原地等待情况下,非逆流个体也是均向出口进行移动,并且形成拱形和半圆形;主原地等待的从个体向主个体移动,远离出口,具有明显逆流行为,等靠近主个体后一同向出口移动;主原地等待的逆流的主个体在从个体未靠近前处于静止状态,等从个体靠近时一同向出口移动。
3.6 结果分析
3.6.1 数据对比
用MATLAB对无逆流、主不原地等待逆流(逆流主从个体人数各为4人)和主原地等待逆流(逆流主从个体人数各为4人)3种情况下,疏散人数随着疏散时间的变化关系进行对比,结果如图7所示。
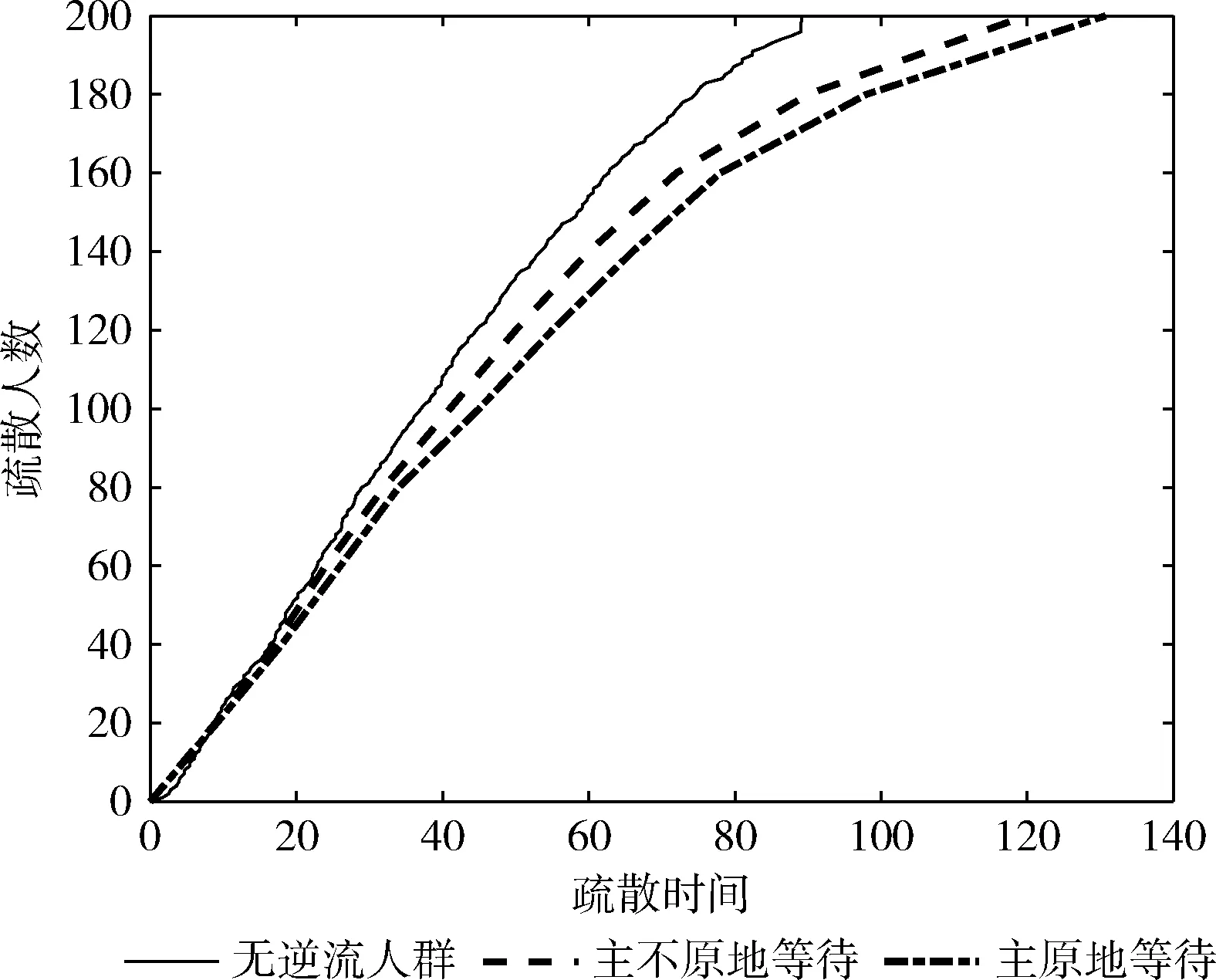
图7 各情况疏散人数随疏散时间的关系
由图7看出,在开始阶段,3种情况的疏散效率相差不多;在疏散的前半段时间内,存在逆流时,因在人群中存在逆流个体,疏散效率比无逆流低;在后半段时间,存在逆流个体的主从个体都向出口移动,此时与无逆流情况相似,因此后半段斜率相差不大,且疏散效率加快;相同条件下,存在主原地等待逆流个体比有主不原地等待逆流个体疏散效率更低。
3.6.2 疏散规律
为研究存在逆流个体时,逆流行为对疏散效率的影响,现在一个出口的情况下,探讨逆流人数(从个体人数)对实验的影响。由于实验数据具有偶然性,因此运行每次实验时,在相同的实验条件下取多次实验数据平均值。在单出口场馆中两种逆流情况总疏散时间随逆流从个体的人数变化如图8所示。
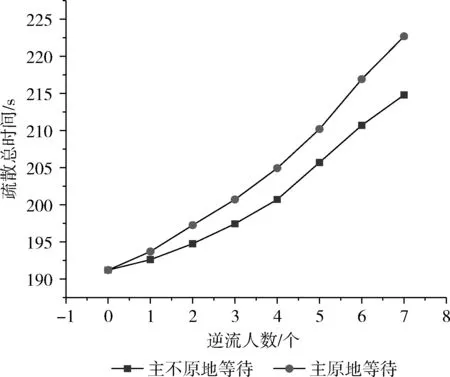
图8 单出口疏散总时间随逆流人数的影响
从图8可看出,在存在主不原地等待逆流行为时,相同条件下,疏散效率比主不原地等待逆流低,疏散时间也相应的增加,对疏散结果影响比较明显;且当逆流的人数越多,相同情况下主原地等待比主不原地等待的影响更明显。
本文提出的基于社会力模型的人员疏散逆流行为仿真模型能够模拟出在人员疏散过程中逆流个体的典型行为,该仿真模型具有一定的可行性,比较符合真实的疏散情景,能够再现和解释真实的人员疏散的情形,模拟出的逆流行为不利于整体疏散的进行。
4 结束语
本文在社会力模型基础上,建立逆流主从个体决策模型,在逆流中主从个体之间加上个体间吸引力,来表示逆流主个体和从个体成员之间的吸引力。通过单出口和多出口场馆进行仿真,结果表明,当人员疏散过程中存在逆流行为时,疏散时间会明显增加,严重影响疏散过程疏散效率;随着逆流人数的增多,疏散效率越低;相同情况下主原地等待比主不原地等待对疏散效果的影响更明显。本文提出的基于社会力模型对逆流行为的仿真具有可行性,在人员疏散仿真的研究上具有较好的效果,对研究人员疏散方案及疏散规律具有参考价值。

