协同智能的蝙蝠差分混合算法

赵志刚，曾 敏，莫海淼，李智梅，温 泰

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

差分进化算法[1](differential evolution algorithm，DE)是由R.tSorn和K.irPec提出的一种基于群体差异的启发式并行搜索方法。作为一种简单、高效的连续空间内全局优化方法，有着和其它基于群体的启发式搜索算法一样的结构简单、易于实现的优点。广泛应用在工程优化问题[2]、大数据分析[3]、云计算[4]、数据分类[5]等领域。

随着进化代数的增加，个体之间的差异化信息逐渐缩小，DE到后期收敛速度变慢，有时会陷入局部最优。为了提高DE的性能，改进的主要方法有：控制参数的改进、差分策略的改进、选择策略的改进、种群重构、混合算法等。拓守恒等[6]将和声算法和差分算法结合，提出了一种混合算法，并用于求解多模态复杂问题；贺军义等[7]基于和声差分进化算法对UKF算法进行改进，并应用于滤波器设计；邹华福等[8]将反向学习的思想引入到差分算法中，提出了一种算法，扩大算法的全局勘探范围；李志敏等[9]以云计算时间最少为优化目标提出了差分人工蜂群算法，以解决云计算资源调度问题；徐俊等[10]提出一种混合差分粒子群算法，来求解任务调度的问题，以更充分利用共享资源；张新明等[11]提出了一种灰狼算法和差分算法的混合优化算法，使用嵌入趋优算子的GWO算法搜索。

为了更好平衡差分算法的全局搜索和局部开发能力，利用蝙蝠算法有较好的局部搜索效果的特点，本文提出了一种蝙蝠算法与差分算法的混合算法。为了验证算法的有效性，使用9个测试函数和5个0-1背包问题，与标准粒子群算法、带高斯扰动的粒子群算法、蝙蝠算法、差分算法、烟花算法相对比。

1 差分进化算法

差分进化算法模拟生物进化，经过一代代循环迭代，保留最优个体，寻找最优解。主要包含了变异、交叉、选择3部分操作。

1.1 参数向量初始化

在D维向量空间里随机产生满足约束条件的M个向量初始化为

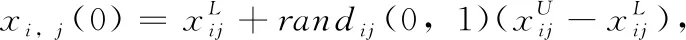
(1)

1.2 基于差分向量的变异

(2)

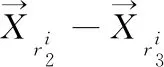
1.3 交 叉

通过交叉操作生成实验向量，增加种群多样性

(3)

其中， 〈〉D表示函数“对D取模”。

2 蝙蝠算法

蝙蝠算法(bat algorithm，BA)[12]模拟蝙蝠觅食来实现算法的迭代和寻优。蝙蝠在捕食过程中利用回声来定位，将各个蝙蝠个体看作可行解，捕食过程看作搜索过程。

2.1 蝙蝠的移动

每个蝙蝠有拥有自己的位置、速度、飞行频率，并可以发出声波。利用所在的位置的目标函数值来评估位置的优劣。蝙蝠种群个体通过速度和飞行频率的变化来进行位移，通过响度和脉冲的变化，来靠近最优解。标准蝙蝠算法使用式(4)至式(6)对飞行频率、速度和位置进行更新

fi=fmin+(fmax-fmin)β

(4)

(5)

(6)

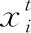
Xnew=Xold+εAVt,ε∈[-1,1]

(7)

其中，ε是[-1,1]范围内的随机数，AVt是当前蝙蝠种群的平均响度。

2.2 响度和脉冲

响度和脉冲会随着寻优过程而发生改变，当蝙蝠逐渐靠近猎物的时候，响度会越来越小，同时脉冲频率会越来越大。蝙蝠算法的响度和脉冲是根据式(8)、式(9)进行更新

(8)

对于任何0<α<1和β>0的情况下都有

(9)

3 差分蝙蝠混合算法

3.1 协同智能

协同智能[13]是指差分种群和蝙蝠种群信息交互、相互协作。蝙蝠觅食时距离猎物越近，其发出的脉冲逐渐大，响度逐渐小，对应算法寻优时越接近最优解，从全局搜索转换为局部搜索。利用蝙蝠算法这一特点，将其与差分算法结合起来，以期动态平衡算法的全局搜索与局部开发的能力。

具体操作为：当第i个蝙蝠种群个体发出的脉冲r(i)小于随机脉冲且响度A(i)大于随机响度时，对差分种群得到的当前最优解gbest进行高斯扰动产生局部解Batx(i)，相当于在gbest附近进行一次详细搜索。并对Batx(i)进行评价，并与差分种群的第i个个体X(i)的适应度值相对比，如果蝙蝠个体更优，则被选入下一代。产生局部解的具体操作如下

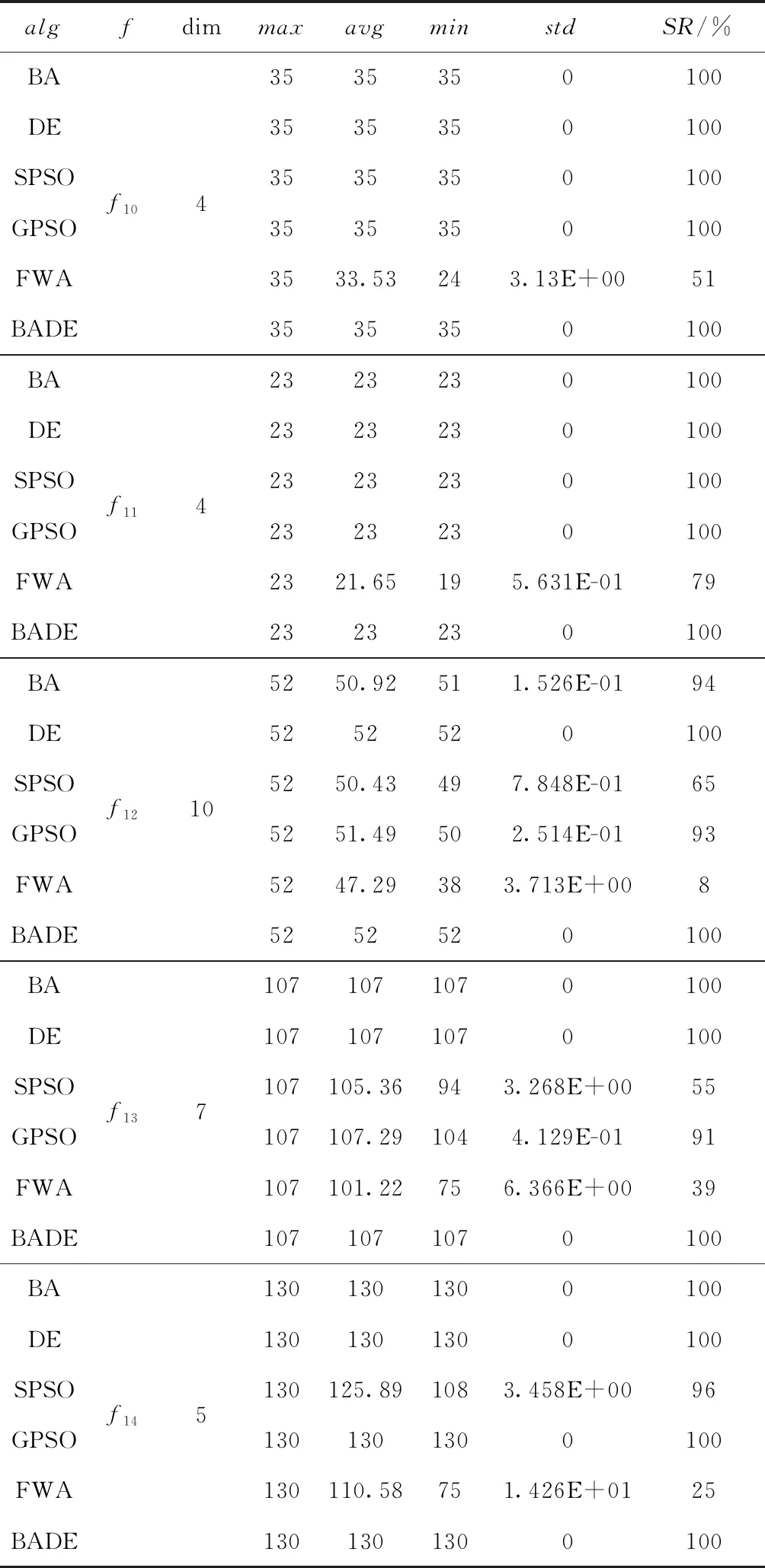
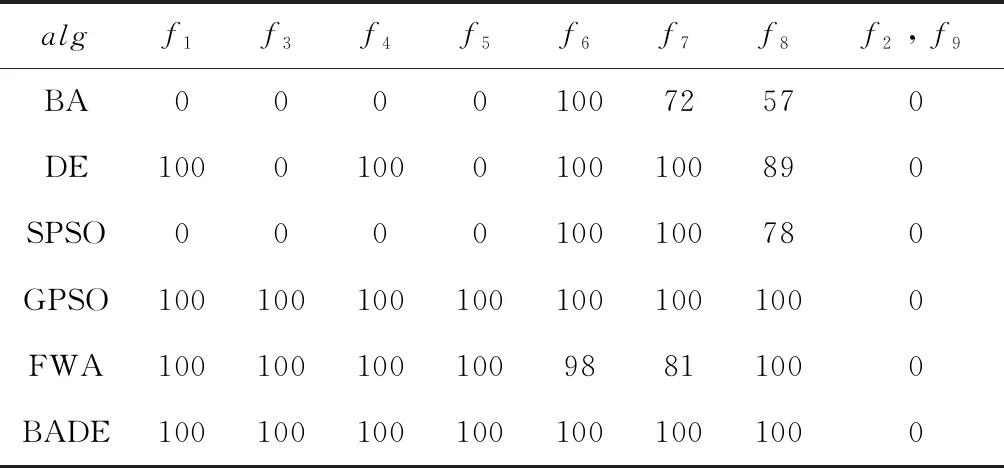
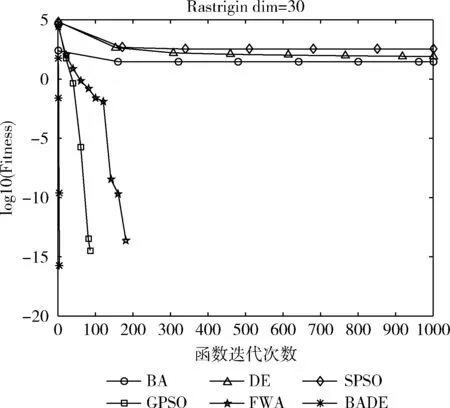
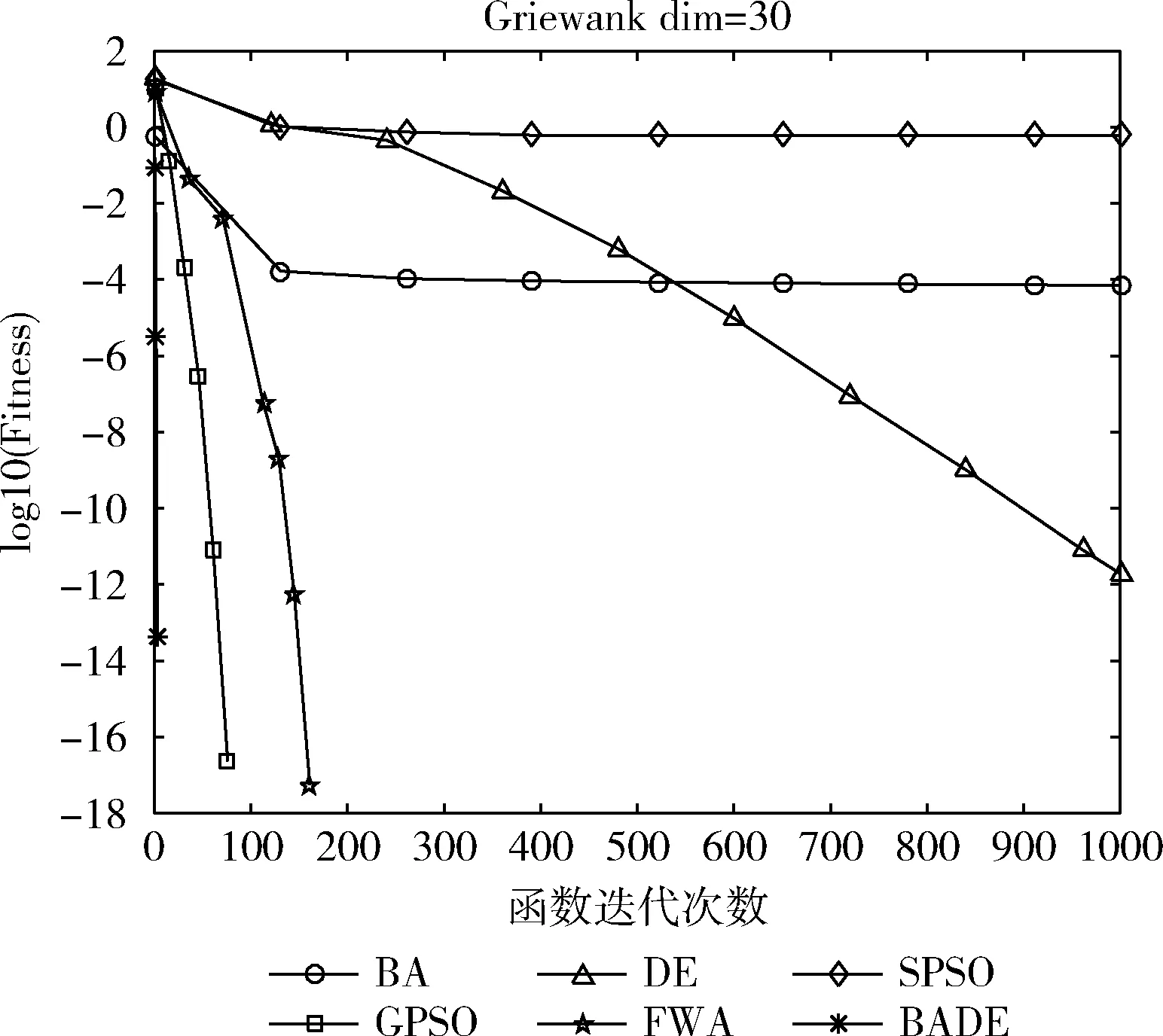
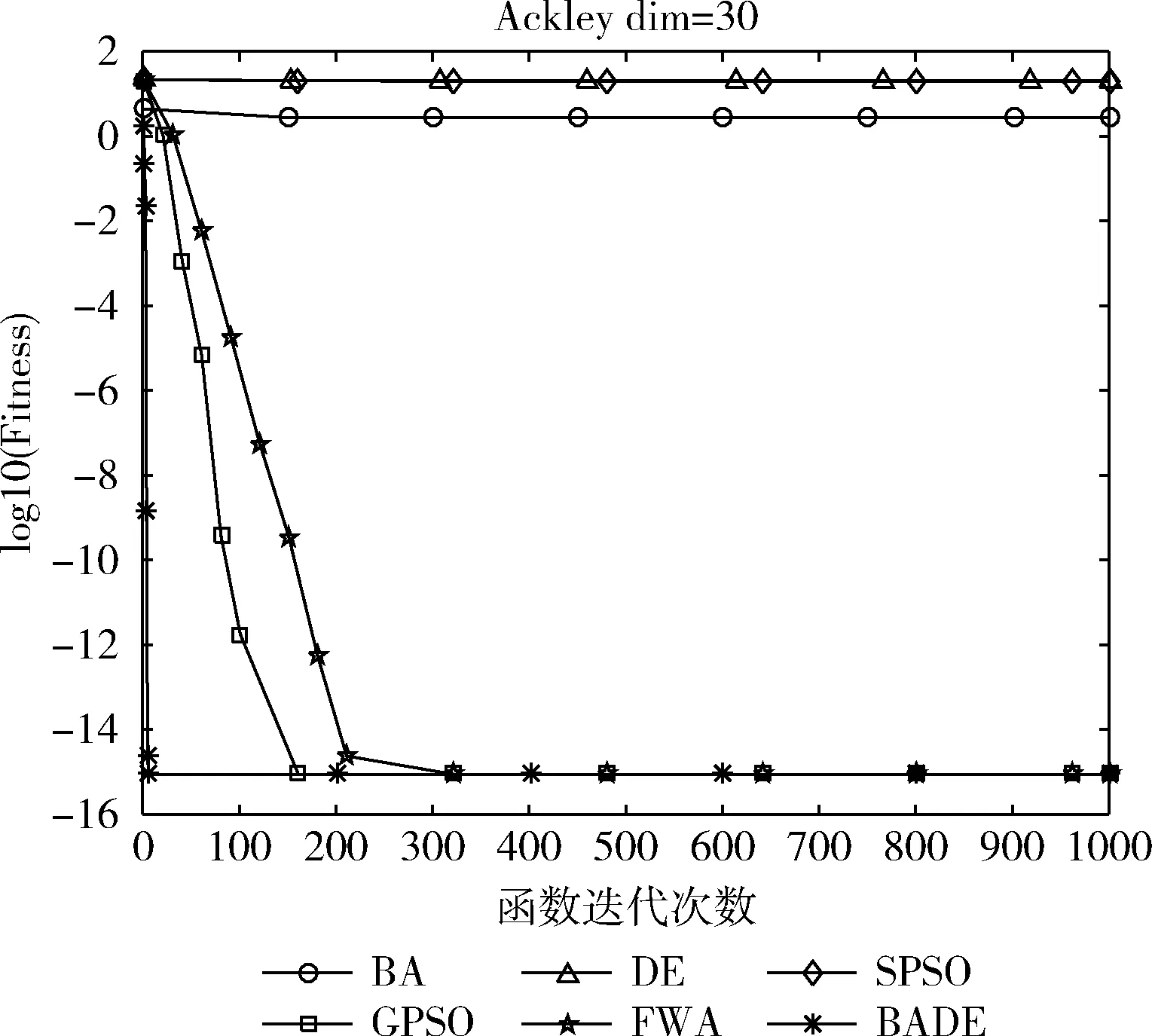
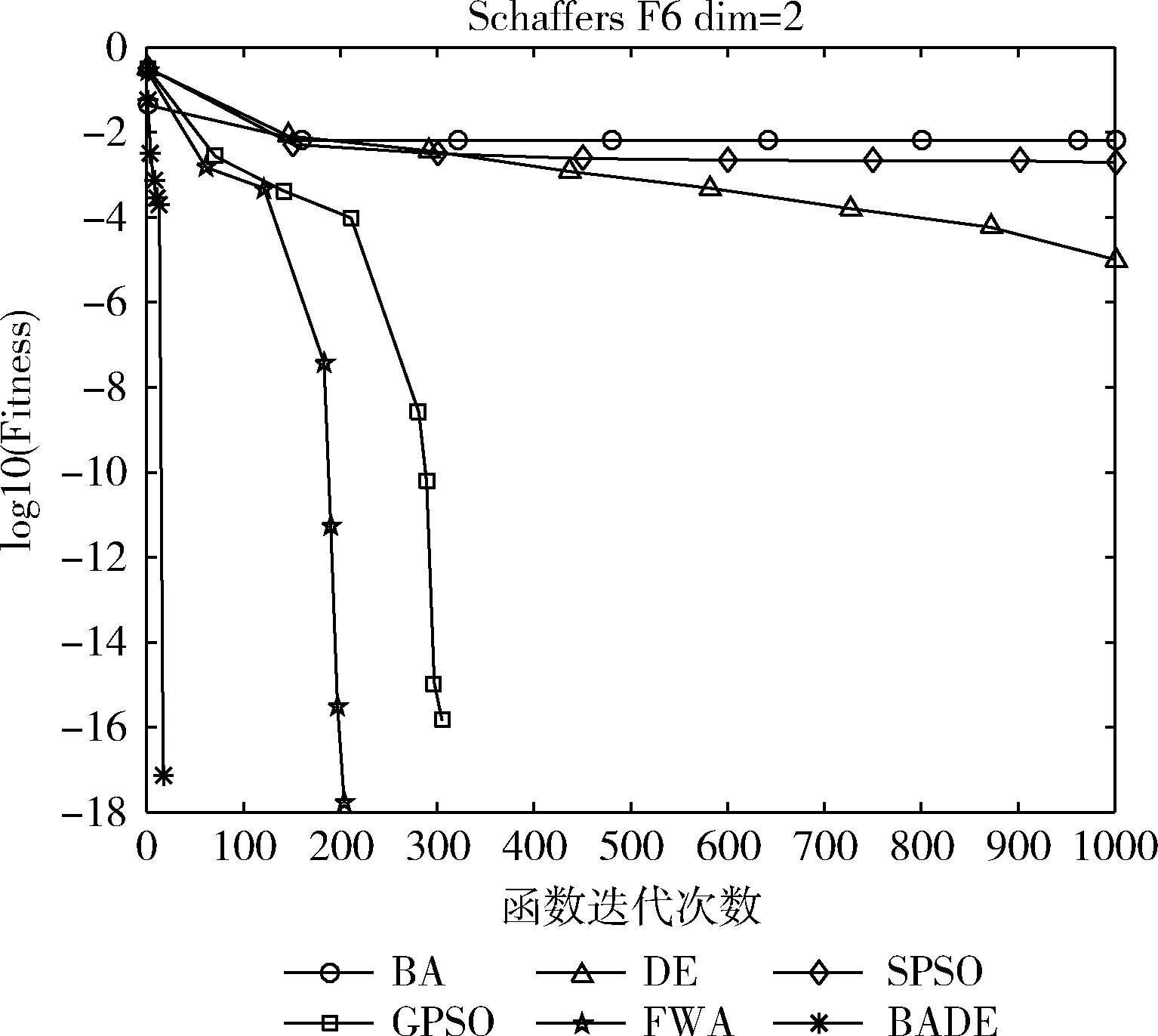
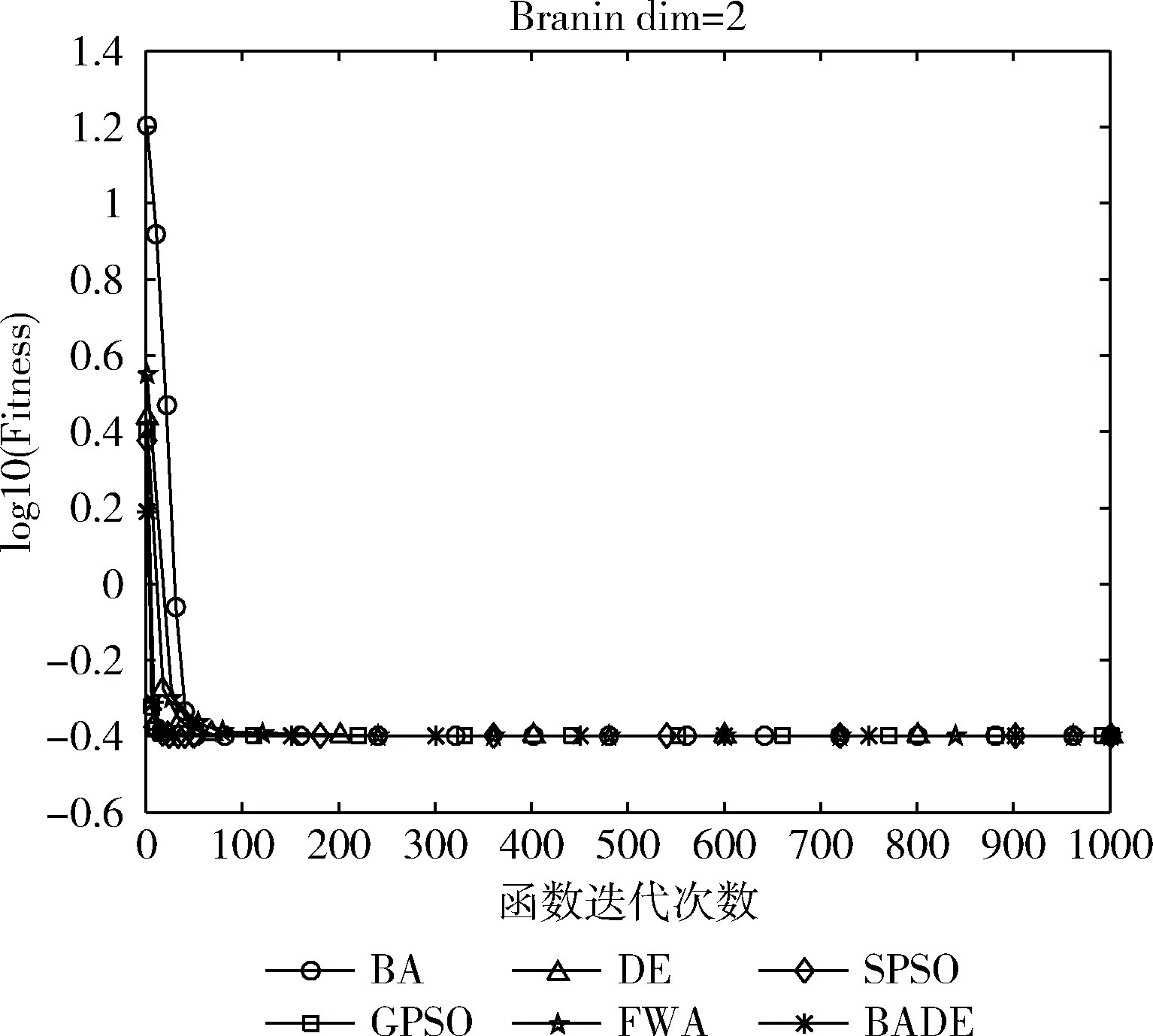
Batx(i)=gbest*(N(0,1)+1),asr(i)

(10)

其中，N(0,1) 是服从均值为0，方差为1的高斯分布函数；r(i) 是第i个蝙蝠发出的脉冲；rand是[0,1]内生成的随机数。

以适应度值来判断局部解的优劣，并以脉冲和响度条件作为约束，当满足式(11)时，局部解将加入下一次迭代，完成蝙蝠种群和差分种群的信息交互

x(i)=Batx(i),asf(Batx(i))rand

(11)

其中，AV(i)是第i个蝙蝠发出的响度。

差分种群与蝙蝠种群协同寻优的伪代码如 Algorithm 1所示：

步骤1 在当前最优解附近产生一个局部解，根据式(10)；

步骤2 对局部解进行越界处理，并计算其适应度值；

步骤3 根据式(8)、式(9)更新响度和脉冲；

步骤4 按照式(11)判断是否将局部解加入下一代；

步骤5 若该局部解优于gbest，则将gbest替换。

3.2 混合算法

综合第1小节的差分算法，以及3.1小节的协同寻优，本文提出了蝙蝠差分混合算法(hybrid bat and differential evolution algorithm，BADE)，BADE混合算法的伪代码如Algorithm 2所示：

步骤1 初始化蝙蝠种群、差分种群；

步骤2 差分种群分别根据式(1)、式(2)、式(3)进行变异、交叉、选择操作；

步骤3 蝙蝠种群协同寻优：Algorithm 1；

步骤4 判断是否接受新解，如果接受，更新gbest；

步骤5 重复步骤2～步骤4的步骤，达到终止条件之后，终止迭代。

4 仿真实验

4.1 测试函数

选用了表1中的9个基准测试来测试混合算法BADE在解决连续型优化问题上的能力，这9个基准测试函数均来自全局优化测试函数库。其中f1～f5的维度为30dim，f6～f9维度为2dim。“*”表示该函数的最优点不止一个。并与标准粒子群算法(SPSO)[14]、带高斯扰动的粒子群算法(GPSO)[15]、蝙蝠算法(BA)[12]、差分算法(DE)[1]、标准烟花算法(FWA)[16]进行对比分析。

表1 基准测试函数

4.2 与其它算法对比

为了避免参数设置的差异对于实验结果产生的影响，保证实验公平与公正，设置种群大小pop=40；寻优精度λ=10-5；最大迭代次数Max_Ite=1000。设置BADE的最大飞行频率fmax=100；最小飞行频率fmin=0.1；其它参数设置参照差分算法与蝙蝠算法。寻优过程中的搜索上界upperBound和搜索下界lowerBound根据不同测试函数具体设置；对比算法的参数设置参考了对应的参考文献。独立重复实验进行100次。

表2给出了6种算法在9个测试函数上进行100次对比实验后的平均结果，worst为最坏值，avg为平均值、std为标准方差。表3给出了6种算法在9个测试函数上的寻优成功率。其中f1～f5维度为30dim，f6～f9维度为2dim。

表2 6种算法对比的实验结果

为了更加直观地观察到收敛情况，给出寻优进化曲线，图1至图5给出了f1～f5的寻优进化曲线；图6至图9给出了f6～f9的寻优进化曲线。图中的纵坐标均为log10(Fitness)，取适应度值的对数，由于Six-Hump Camel-Back测试函数的最优值为负数，因此不取对数，为适应度原始值。

4.3 收敛性分析

在测试函数f1、f3、f4、f8的优化过程中，分析图1、图3、图4、图8：在寻优前期，在相同迭代次数情况下，BADE算法的收敛速度和收敛精度均优于其它5种算法。分析表2对应的平均解avg：BADE找到了最优值，且不亚于其它5种算法。

表3 f1～f9:6种算法寻优成功率

图1 f1寻优进化曲线

图2 f2寻优进化曲线

图3 f3寻优进化曲线

图4 f4寻优进化曲线

图5 f5寻优进化曲线

图6 f6寻优进化曲线

图7 f7寻优进化曲线

图8 f8寻优进化曲线

图9 f9寻优进化曲线

在测试函数f2、f5的寻优过程中，分析图2、图5：在寻优前期，迭代次数相同，BADE的收敛速度和收敛精度均优于其它5种对比算法；在寻优后期，6种算法均陷入局部最优。分析表2对应的平均解avg：迭代结束时，对于f2， BADE寻找到的平均解avg优于其它5种算法；对于f5， BADE寻找到的平均解avg不亚于其它5种算法。

在测试函数f7的寻优过程中，分析图7：BADE在寻优前期的收敛速度和收敛精度不亚于其它5种算法；分析表2对应的平均解avg：在迭代结束时，寻找到的平均解也不亚于其它5种算法。

在测试函数f6、f9的寻优过程中，分析图6、图9：在寻优前期，BADE的收敛速度和收敛精度略优于其它5种算法。分析表2对应的平均解avg：迭代结束时，BADE算法的平均解avg不亚于其它5种算法。

综上，BADE算法的总体收敛性能优于其它5种算法。

4.4 寻优成功率分析

设置寻优精度λ=10-5，寻优成功定义为：寻找到的最优解与理论最优解差值小于该寻优精度。由表3的寻优成功率可知：对于f2和f9， 6种算法均没有找到理论最优解。对于f1、f3、f4、f5、f6、f7、f8， BADE的寻优成功率均为100%优于其它5种对比算法。

综上，BADE的总体寻优成功率优于其它5种对比算法。

4.5 鲁棒性分析

算法鲁棒性可从标准方差std的大小反映出来，方差越小，鲁棒性越好；反之，算法的鲁棒性也就越差。分析表2中标准方差std一栏，在f1、f3、f4、f5、f8的寻优过程中，BADE算法的标准方差std均为0，表现出较好的鲁棒性。在f2寻优过程中，标准方差std比BA、DE、SPSO、GPSO小，略大于FWA；在f6寻优过程中，BADE的标准方差std比BA、SPSO、FWA小，略大于DE和GPSO；在f7、f9寻优过程中，标准方差std比BA、FWA小，略大于DE、SPSO、GPSO。

综上，BADE的总体鲁棒性优于其它5种对比算法。

4.6 讨 论

BADE混合算法表现出较好的性能主要是由于以下原因：

第一，利用蝙蝠回声定位的特点，加强对当前最优解附近的局部搜索，加快了收敛速度;

第二，差分种群与蝙蝠种群个体在整个寻优过程中，协同交互，及时反馈，加强了信息交互，做到协同智能；

第三，高斯扰动提高了种群多样性，有效防止了迭代过程中因陷入局部最优而导致的更新停滞，有利于跳出局部最优。

本文提出了一种蝙蝠差分混合算法，其主要思想是利用蝙蝠回声定位的特点，在当前最优解附近进行详细的局部搜索，同时高斯扰动的加入提高了种群多样性。双种群在寻优过程中，可以信息交流，优势互补，有效平衡了全局搜索和局部开发能力，在求解精度和稳定性表现出较好的性能。

5 算法应用

5.1 0-1背包问题

鉴于BADE在连续优化问题上有较好的表现，将BADE应用于离散优化问题是个合理的方向，离散优化是最优化领域的一个非常重要的方面，是应用数学和计算机科学中优化问题的重要分支。0-1背包问题(knapsack problem，KP)是典型的整型优化问题，数学模型如下

(12)

(13)

其中，n是物品数量，pi是第i个物品的价值，vi是第i个物品的体积，Vmax是背包的最大容量，xi是第i个物品的状态，0表示不被装进背包，1表示被装进背包。不允许部分装入也不允许重复装入。

0-1背包问题求解的是在背包最大容量限制下，使得装入物品的总价值最大。将问题转换成最小化问题[18]，目标函数为

(14)

5.2 算法离散化设计

0-1背包问题属于离散类型问题，在算法应用时应将差分种群个体以及蝙蝠种群个体的位置信息进行离散化

(15)

其中，x′(i,j) 是离散前位置，x(i,j) 是离散后位置。

BADE混合算法求解0-1背包问题的具体操作如Algorithm 3所示：

步骤1 初始化蝙蝠种群、差分种群；

步骤2 差分种群分别根据式(1)、式(2)、式(3)进行变异、交叉、选择操作；

步骤3 按照式(15)对当前位置信息进行离散化处理之后，按照式(14)评估适应度值；

步骤4 按照式(10)在gbest附近高斯扰动，产生局部解，按照式(15)离散化处理，按照式(14)评估适应度值；

步骤5 更新响度和脉冲；

步骤6 判断是否接受新解，如果接受，更新gbest；

步骤7 重复步骤2～步骤6，达到终止条件，则终止迭代。

5.3 对比实验

对于其它5种对比算法(BA，DE，SPSO，GPSO，FWA)进行同样的离散化处理之后，对实验结果进行比较。选用了表4中的5个常见0-1背包问题[17]。

表4 5个常见背包问题

5.4 实验结果与分析

参数设置：最大迭代次数max_it=500；独立重复运行次数run_num=50；其它参数设置参照4.3小节，对比实验的结果见表5。

表5的实验结果显示：由max这一栏可知，6种算法对于这5个0-1背包问题都能找到最优解f*； 由std这一栏可知：只有BADE对于这5个0-1背包问题对应的标准方差值均为0，这反映了BADE对于其它5种算法具有更优的鲁棒性；由SR这一栏可知：BADE对于其它5种算法具有更高的寻优正确率。综上，BADE算法在求解表5中给出的5个常见的0-1背包问题时，总体性能优于其它5种对比算法。

6 结束语

利用蝙蝠种群和差分种群的协同智能，本文提出了一种混合算法——蝙蝠差分混合算法。高斯扰动能够增加种群的多样性，避免算法陷入局部最优。协同智能能够有效的平衡全局搜索和局部开发能力。通过仿真对比实验，我们验证了蝙蝠差分混合算法具有较好的寻优能力，有着更快的收敛速度和更好的收敛精度。在未来研究工作中，将尝试从理论研究角度对将蝙蝠差分混合算法的收敛性进行分析，并与其它工程应用相结合。

表5 5个0-1背包问题的实验对比结果