基于多效用阈值的分布式高效用序列模式挖掘
曾 毅,张福泉
(1.广西大学行健文理学院 计算机与信息工程系,广西 南宁 530005; 2.北京理工大学 计算机学院,北京 100081)
0 引 言
频繁模式挖掘问题是当前数据分析领域的一个研究热点,许多现实问题中可通过频繁模式挖掘对数据实现有效的分析,提取出感兴趣的信息[1]。话题预测、金融行情的预测、购物篮问题等均为频繁项集挖掘的主要应用领域[2]。频繁项集挖掘支持向下闭包属性,该属性可在剪枝过程中极大减少后续项集的数量,提高挖掘的效率。而高效用项集挖掘[3]并不支持向下闭包属性,因此剪枝过程中保留了过多的候选项集。许多应用将事务以序列形式存储于数据库中,组成了序列数据库[4],序列模式的搜索空间明显大于其它模式,其计算复杂度也明显大于其它模式类型。
在高效用序列模式的挖掘问题中,提高剪枝的效率与搜索的速度一直是决定挖掘效果的关键指标[5]。文献[6]提出时空效率均显著提升的高效用序列模式挖掘算法,该算法提出1-2-UM和2-2-UM的效用信息列表结构,快速剪枝非候选序列。文献[7]提出了简洁的高效用模式挖掘算法,该算法设计了LIT结构保存效用信息,实现了高效的剪枝策略。文献[8]对候选模式自动计算最适合的间隔约束,并且设计了3种剪枝策略来提高算法的执行效率。文献[6-8]对于蛋白质序列、DNA序列、行为序列等小规模数据集表现出较好的效果,但是对于大规模数据集未能实现理想的效果。
为了提高高效用序列模式挖掘算法对于大规模数据集的处理效果,设计了基于多效用阈值的分布式高效用序列模式挖掘算法。该算法采用纯数组结构维护效用信息,采用前缀树trie-tree维护序列模式,这两种数据结构有效地提高挖掘过程的时空效率。设计了初步剪枝策略与深度剪枝策略,递归地从1-项集与2-项集中排除非候选模式。算法在评估前缀树节点的过程中,各个节点的挖掘顺序独立于其它同级节点,所以可以并行地处理前缀树中的所有子节点,并且不会影响结果。据此给出了本算法的分布式实现方案,能够在云计算、GPU(graphics processing unit)、多核处理器等平台上实现并行计算,从而实现快速的挖掘处理。
1 问题模型
设I={i1,i2,…,in} 为一个项集的集合,in为一个项集,设s={e1,e2,…,er} 为一个定量序列,表示一个按时间升序排列的定量模式列表,ej(1≤j≤r) 为一个模式,序列的每个模式ej描述为一个序列形式 (x1,x2,…,xm),xk(1≤k≤m) 为一个定量的项。定量序列的数据库SDB由若干的定量序列会话集组成,即SDB={s1,s2,…,sz},sy(1≤y≤z) 为SDB的第y个序列。序列sy包含一个元组 (SIDy,γy),SIDy为序列的ID,γy为sy序列的内容。如果l=|s|, 那么序列s称为l-序列,其中|s|=∑ej∈s|ej|, |ej| 为模式ej中的项数量,l为序列s的长度,序列的大小定义为序列中包含的模式集数量,表示为r。
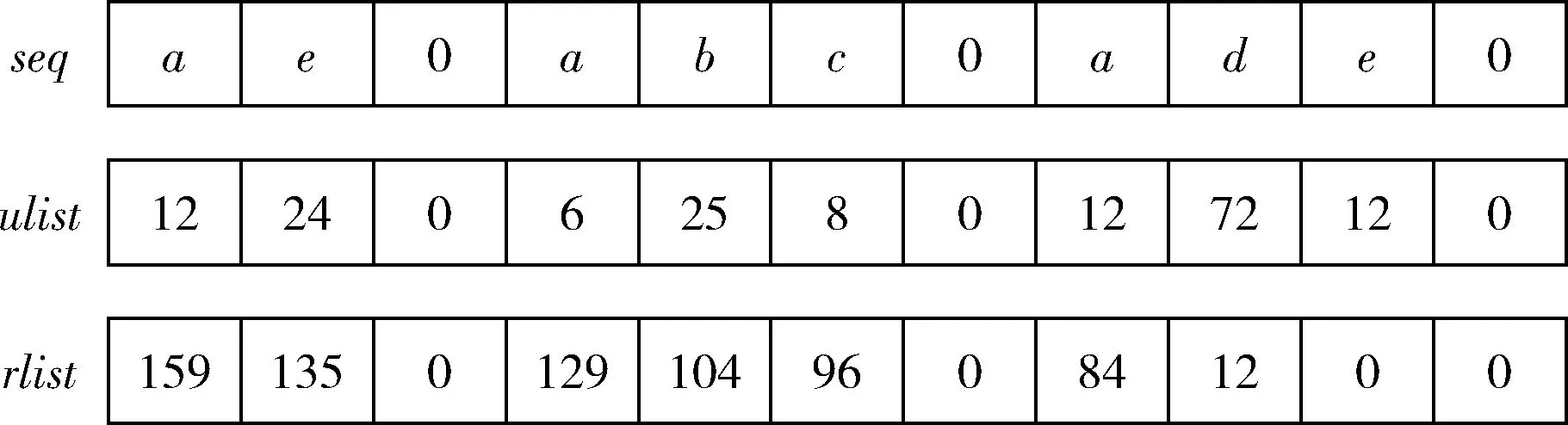
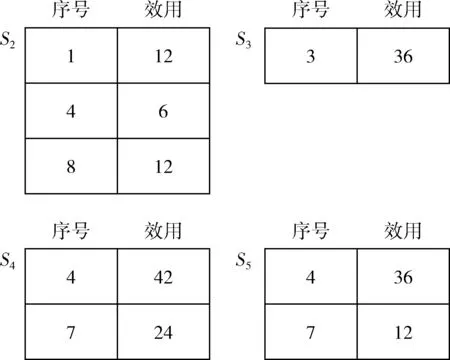
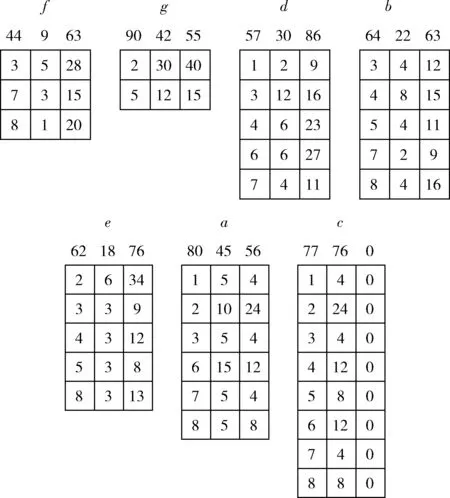
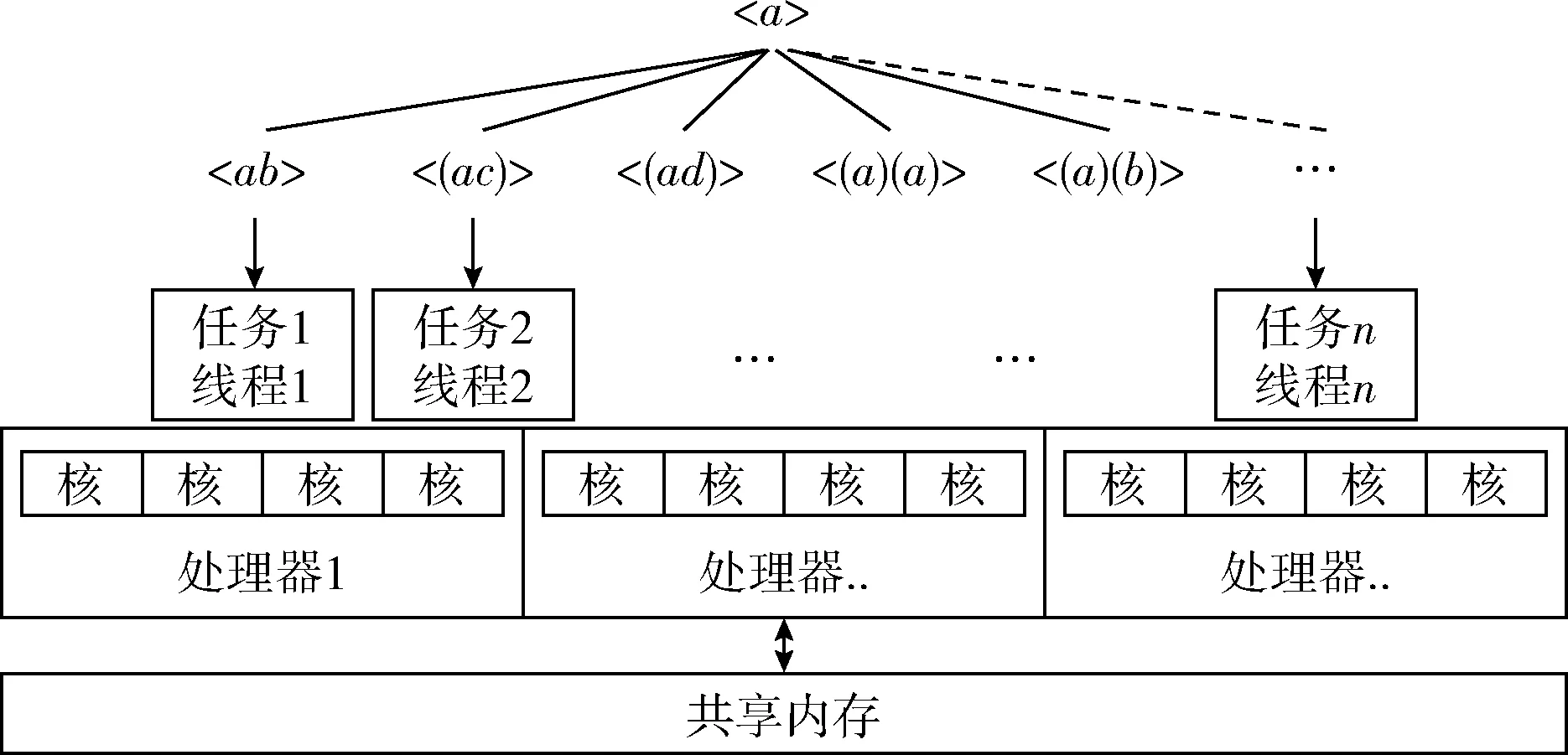
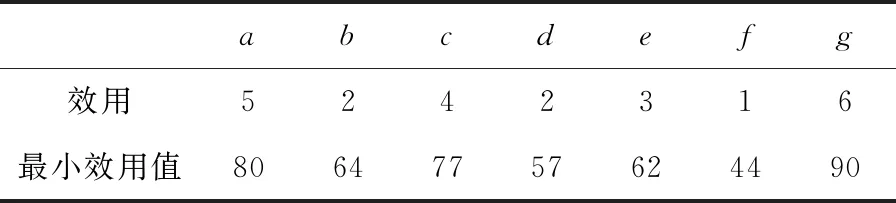
设α= 表1 会话数据库实例 表2 项的利润与最小效用阈值 定义1 序列s中项ij的内部效用定义为s中ij全部定量的总和,记为iu(ij,s)。 最大内部效用定义为s中ij的最大值,记为iumax(ij,s)。 项ij的外部效用定义为项ij的外部权重(例如:超市购物篮模型的利润),记为eu(ij)。 定义2 序列s中项ij的效用定义为外部效用与内部效用的乘积,记为u(ij,s)=eu(ij)×iu(ij,s)。 定义3 序列s中项ij的最大效用定义为外部效用与最大内部效用的乘积,记为umax(ij,s)=eu(ij)×iumax(ij,s)。 定义4 序列s的效用定义为序列s中所有项的效用总和,记为 (1) 定义5s中模式p的效用定义为s中p的最大效用,记为u(p,s)。 定义6SDB中模式p的实际效用定义为SDB所有序列的模式效用之和,记为 (2) 定义7 序列数据库SDB的效用定义为SDB所有序列的效用之和,记为 (3) 定义8 最小效用阈值的百分比记为δ,最小效用阈值记为MIU,定义为 λ=δ×su(SDB) (4) 定义9 模式p的序列加权效用(sequence weighted utility,SWU)定义为SDB中所有p的序列效用之和,记为SWU(p)。 如果SWU(p)≥λ, 则称p为高效用序列模式 (5) 定义10 满足以下3个条件的数据结构定义为字典树trie-treeT:①T的每个节点包含一个序列与其效用值,根节点为空。②T中每个节点p的子节点可分为I-级联形式或者S-级联形式。③T的所有节点按照字母顺序升序排列。本文修改了trie-tree结构,根节点设为“<>”,其它节点包含SDB中所有序列的模式与效用值,称为索引效用列表。 大多数算法[9]使用效用矩阵与剩余效用矩阵分别保存序列的效用与剩余效用,效用矩阵存储效用值的效果较好,但是需要消耗大量的内存。为了解决这个问题,设计了纯数组的效用数据结构,减少了内存的消耗。将序列的效用与剩余效用分别保存于3个数组中,分别称为会话序列数组、效用数组与剩余效用数组。 定义11 分界项定义为将序列分为子项集的项,记为ditem,ditem的值设为0。 定义12 会话序列数组定义为保存s中所有项的一维数组,记为seq,seq的大小等于s的大小r加s的长度l。seq中索引i的元素表示为seq[i],其中seq[i]为索引i的项。 定义13 给定一个序列s,项i在s中索引j的外部效用定义为i对于j的定量,记为iu(i,j,s)。 定义14 效用列表定义为保存序列s所有项效用的一维数组,记为ulist,ulist的大小等于s的大小r加s的长度l。 定义15 剩余效用记为ru,剩余效用列表定义为保存序列s所有项剩余效用的一维数组,记为rlist。rlist的大小等于s的大小r加上s的长度l。rlist中索引i的项剩余效用等于在ulist中j>i的项集效用之和 (6) 图1是3个列表的例子,seq、ulist、rlist这3个列表中的分界项分别为索引3、7、11,序列中e的第一个索引为2,因此ulist中e的效用为ulist[2]=iu(e,2,S2)×eu(e)=6×4=24。 索引5的剩余效用值为rlist(S2)[5]=ulist[6]+ulist[8]+ulist[9]+ulist[10]=8+12+72+12=104。 图1 3个列表的例子 定义16 序列模式的索引记为ilist(p)。假设序列s包含n个模式,每个模式为p= 本文设置一个索引效用列表保存p的所有索引与效用。 定义17 给定一个模式p,对p进行I-级联或S-级联操作获得超模式p′,s中索引i处的索引效用值定义为p′的索引效用值,记为iulist(p′,i,s) iulist(p′,i,s)=max{iulist(p,j,s)|∀p的序号ins∧j∧i}+ulist(s)[i] (7) 定义18 序列s中模式p的索引效用列表记为iulist(p),定义为 (8) SDB中模式p的索引效用列表定义为 (9) 定义19 序列s中模式p的前缀效用记为peu,定义为 (10) 式中:模式p的peu定义为 peu(p,s)=max{peu(p,i,s)|∀iins} (11) 定义20 节点p的效用上限记为peu,节点p在trie-Tree的子节点上限也是peu。如果peu(p)<λ, 那么可安全地剪枝p的子树,缩小挖掘程序的搜索空间。SDB中模式p的peu定义为 (12) 定义21 减少的序列效用记为rsu,对模式p进行I-级联或者S-级联处理产生超模式p′,序列s中p的rsu定义为 (13) SDB中序列p的rsu定义为 (14) 算法对序列p进行I-级联或者S-级联处理需要获得超序列p′的iulist。考虑一个1-项模式a,模式a同时出现于序列S2,S3,S4,S5中。S2中a分别出现于索引1、4、8处,对应的效用分别为12、6、12。S2、S3、S4、S5的iulist(a)如图2所示。 图2 序列iulist的例子 包含a的序列中通过I-级联与S-级联对a进行扩展。考虑序列ae,从iulist(a)生成iulist(ae)。S2中ae出现于索引2与10处,其效用值分别为12+24=36、12+12=24。采用上述方法可获得S3、S4与S5的iulist(ae),最终的iulist(ae)如图3所示。 图3 最终的iulist例子 从iulist(a)也可产生iulist(ae)。S2中ae出现于索引10处,而S2中a出现于索引1、4处,效用值分别为12与6。模式a也出现于S2的索引8处,但是并未生成该索引的ae,即iulist(ae,10,S2)=max(12,6)+12=24。 以相同的方式建立S4的iulist(ae),最终的iulist(ae)如图4所示。 图4 最终的iulist(ae)例子 采用I-级联与S-级联从序列p产生p′的过程中,仅仅扫描了序列中p之后的子序列,节约了扫描的时间。 如果算法在构建候选序列集之前,初步剪枝S-级联与I-级联的项,则可以加快挖掘程序的速度。考虑算法第一阶段的1-项模式集,每个模式p包含1个项i与其peu值,表示为peu(i)。第一阶段的iulist为空,根据定义20计算peu(i)值,如果项i满足peu(i)<λ,那么称之为低效项。提出一个剪枝策略来过滤S-级联与I-级联项集的低效项。 定义22 效用的上限记为euu(s′),假设s′为序列s的超序列,那么euu(s′)定义为 euu(s′)=u(s)+peu(i) (15) 理论1 给定一个序列s,其超序列为s′,如果s是s′的前缀或者s′=s, 那么u(s′)≤euu(s′)。 证明:设s′为序列s的超序列,那么u(s′)=u(s)+u(i), 可得u(i)≤peu(i)。 因此u(s′)≤u(s)+peu(i), 且u(s′)≤euu(s′)。 根据理论1,euu(s) 是s的效用上限,所以当euu(s)<λ, 可在不影响挖掘结果的情况下对s前缀的超序列进行安全的剪枝。 定义23 后缀最小效用记为SMU,定义为 SMU(p)=min(MIU(p),MIU(ext(p))) (16) 式中:ext()为模式的级联扩展,MIU为模式的最小效用。 定义24 引入文献[10]的估计效用共生结构,记为EUCS,EUCS是一个三角矩阵,其2-项集入口定义为 EUCS(X={xi,xj})=TWU(X={xi,xj}) (17) 式中:xi与xj为2-项集的两个项。 SHEPMA算法的伪代码如算法1所示。第一阶段,SHEPMA聚集所有的1-项模式,根据SWU过滤低效用的项,同时删除数据库中的空序列。第二阶段,初始化搜素空间p=NULL,iulist(p)=φ,asu(p)=0, 然后基于候选项集生成iulist。如果peu(p)小于λ,则搜素模式p的父节点,扫描p的投影数据库,发现其中I-连接或S-连接的项。根据理论1初步删除两个列表中的低效项,根据定义22计算euu(p′),如果满足条件,则将该模式分别放入i-exts与s-exts两个列表中。使用定义6的asu剪枝剩余的低效项。对于i-exts中的I-连接项,通过I-连接产生p′与iulist,如果序列p′的效用大于λ,则直接输出p′。 算法1:SHEPMA算法 输入: 序列数据库SDB, 最小效用阈值λ, 前缀p, 索引效用列表iulist(p),asu(p) 输出: 前缀p的HUSP集 (1) IFpeu(p)<λTHEN (2) RETURN NULL; (3) 一次扫描p-投影数据库; (4)IFeuu(p′)≥λTHEN (5)i_exts← I-级联项; (6)s_exts← S-级联项; (7)删除i_exts与s_exts中的低rsu项; (8)FOREACH 项i∈i_extsDO (9)p′←I_concatenation(p,i); // I-级联 (10) 建立iulist(p′); (11) IFasu(p′)≥λTHEN (12) RETURNp′; (13)SHEPMA(p′,iulist(p′),asu(p′)); (14)FOREACH 项i∈s_extsDO (15)p′←S_concatenation(p,i);//S-级联 (16) 建立iulist(p′); (17) IFasu(p′)≥λTHEN (18) RETURNp′; (19)SHEPMA(p′,iulist(p′),asu(p′)); 设计了适用于分布式挖掘程序的效用列表数据结构。项集的效用列表中包含以下两个信息:①项集的主要信息MIU(p),u(p),ru(p), ②三元组格式的序列信息 图5是修改后的1-项集效用列表,例如:模式f的MIU(f)=44,u(f)=9,ru(f)=63。f出现于序列3、7、8中,因此f的效用列表包含3个入口,每个入口包含序列的效用值与剩余效用值。例如:模式f出现于序列3中,效用值为5,剩余效用值为28。模式f出现于序列7中,效用值为3,剩余效用值为15。 图5 修改的1-项集效用列表 针对多阈值的分布式HUI挖掘问题,补充了3个新的剪枝属性,对HUI进行深度的剪枝处理。 属性1:TWU-属性。如果TWU(p) 证明:根据apriori属性[11]:Sup(X′)≤Sup(X), 说明TWU(X′)≤TWU(X) 例:设一个项集为X={fde}, 表1中项集fde出现于序列3中,TWU(fde)=33 属性2:SMU-属性。如果模式p的后缀效用总和小于SMU(p), 那么p的超集都不是HUI。如果u(p)+ru(p) 例:设一个项集为p={fe}, 表1中项集fe出现于序列3与8中。fe的效用与剩余效用分别为u(fe)=(5+3)+(1+3)=12、ru(fe)=(9+13)=22。u(fe)+ru(fe)=12+22=34, 满足条件u(fe)+ru(fe) 属性3:EUCS-属性。如果2-项集X的EUCS小于SMU(X),那么X的超集均不是HUI。 证明:因为EUCS(X={xi,xj})=TWU(X), 可得TWU(X′)≤TWU(X)。 如果EUCS(X)=TWU(X) 例:表1中EUCS(X={gb})=TWU(gb)=27,SMU(gb)=min(MIU(gb),MIU(ext(gb)))=min(MIU(gb),MIU(eac))=min(64,62)=62。 因为EUCS(gb) 在SHEMA算法的不同阶段应用上述3个剪枝属性,以提高HUI的挖掘效率。 SHEMA算法的输入为会话数据库D,最小效用阈值MMU。首先扫描数据库,计算所有1-项集的TWU值,第2次扫描数据库,进行以下的剪枝操作:步骤①应用TWU-属性(属性1)处理,然后重新计算候选项集的TU值;步骤②计算所有候选1-项集的EUCS;步骤③构建1-项集的效用列表。 算法2所示是SHEMA主程序的伪代码,第(1)-(12)行是扫描数据库的关键操作。之后explore_search_tree()函数搜索候选项集,挖掘所有的HUI。 算法3是前缀树的搜索程序,如果项集X满足TWU-属性,那么搜索X的前缀树。算法3的第(6)行应用了EUCS剪枝机制,在项集X与Y的效用列表构建之前缩小了候选项集的空间。搜索过程中项集X与Y具有相同的前缀,所以在应用EUCS属性的时候,排除相同的前缀项P(算法3的第(6)行)。 算法2:SHEMA算法的主程序 输入: 输入数据库D, 多个最小效用阈值MMU。 输出:HUI集 (1)扫描D, 计算所有1-项集的TWU; (2)foreachTj∈Ddo (3)Tj中xi按照TWU值升序排列; (4)TUj=0 /*重新计算TU值*/ (5) foreachxi∈Tjdo (6) ifTWU(xi)≥SMU(xi) then /*TWU-M-Prune属性*/ (7)TUj=TUj+U(xi,Tj); (8) foreachxi∈Tjdo (9) foreachxk∈Tj/xido (10)EUCS(xi,xk)=EUCS(xi,xk)+TUj; (11) 建立1-项集UL; (12)按照TWU值将1-项集UL升序排列; (13)HUI=explore_search_tree({},UL,MMU); 算法3:explore_search_tree函数 输入:P(前缀项集P的UL),UL(所有P的UL集),MMU(多个最小效用阈值) 输出: 前缀为P的所有HUI (1)foreach 效用列表XinULdo (2) ifU(X)≥MIU(X) thenHUI={HUI∪X}; (3) ifU(X)+RU(X)≥SMU(X) then (4)exUL={}; (5) foreachX之后的效用列表YinUL (6) ifEUCS(X-P,Y-P)≥SMU(X) then (7) ifUL(XY)≠NULL (8)exUL={exUL∪UL(XY)}; (9)explore_search_tree({},UL,MMU); SHEMA算法使用广度优先搜索(breadth-first search,BFS)遍历前缀树。SHEMA算法评估前缀树节点的过程中,各个节点的挖掘顺序独立于其它的同级节点,所以前缀树中任意节点的所有子节点可以同时被处理,并且不会影响结果。 图6是SHEMA分布式的一种实现方案。为每个候选序列会话p′建立一个并行的任务(进程),并且放入进程列表tasklist中[12],通过多核处理器分布式地处理tasklist内的所有任务,设置一个同步机制保证分布式任务的同步性。采用共享内存机制保存候选项集。 图6 SHEMA分布式挖掘 通过算例解释SHEMA算法的关键步骤。算法共有两个输入量:序列数据库D与多个最小效用值MMU。假设输入的序列数据库见表3,最小效用值见表4。 表3 会话数据库例子 表4 模式效用与最小效用阈值 首先计算所有1-项集的SWU值,项a-g的SWU值分别为186、128、242、124、180、72、97。然后遍历每个会话,选出候选1-项集并计算其EUCS值。 序列中的模式按照SWU值排序,获得的1-项列表为f,g,d,b,e,a,c,排序后的会话见表5。 表5 排序后的会话入口 计算所有候选1-项集的EUCS,例子中有7个1-项集,因此建立的三角矩阵共有21个入口。例:EUCS(gb)=27、EUCS(ge)=97、EUCS(fa)=72。 处理完所有会话,更新1-项集的效用列表,图1是例子的1-项集最终效用列表。 基于1-项集效用列表挖掘HUI,在后续的处理中无需再访问原数据库。通过深度优先搜索(DFS)搜索1-项集效用列表,首先,结合1-项集f与其它的1-项集效用列表产生2-项集,然后基于EUCS属性删除其中低效的模式。使用前缀f的2-项集递归地产生3-项集。重复上述搜索过程直至所有的1-项集均作为前缀,在递归处理过程中,检查HUI并且添加到HUI列表中。表6是最终产生的HUI。 表6 最终产生的HUI 实验环境为Dell PC机,配置为Intel Xeon 3.7 GHz处理器、64 GB主内存,Linux操作系统。基于Java语言编程实现各个挖掘算法。选择3个同类型的挖掘算法作为对比文献,分别为MaHUSPM[13]、MSPC[14]、MHHUSP[15],MaHUSPM是一种以降低内存消耗为目标的挖掘算法,MSPC是一种以删除冗余候选模式为目标的深度剪枝策略,MHHUSP是一种以加速挖掘速度为目标的隐藏模式挖掘算法。 采用两个公开数据集作为benchmark数据集,分别为Ta-Feng grocery[16]数据集与Kosarak[11]数据集。Ta-Feng grocery[16]为购物记录组成的序列数据库,Kosarak[11]为博客记录组成的序列数据库。Kosarak包含99万个序列,规模较大,Ta-Feng包含3万多个序列,规模中等。表7两个数据集的基本信息。 表7 实验数据集的基本属性 首先评估SHEMA算法剪枝策略的效果,统计4个挖掘算法产生的候选项集数量。图7是4个挖掘算法对于Ta-Feng grocery与Kosarak两个数据集的剪枝效果,图7(a)中δ=0.06045,图7(b)中δ=0.0045。图7(a)显示,对于中等规模的数据集,SHEMA算法在不同模式长度下的候选模式数量均低于其它3个挖掘式算法,本算法的3个剪枝属性效果较好,明显地缩小来了序列的搜索空间。图7(b)显示,对于大规模的数据集,其它3个算法随着序列数量的增加而迅速增长,但本算法缓慢提高。主要原因在于SHEMA算法在1-项集与2-项集阶段设计了深度的剪枝策略,有效地抑制了候选模式的保留量。 图7 4个挖掘算法对于Ta-Feng grocery与Kosarak 两个数据集的剪枝效果 缩小候选项集数量的关键目标是降低模式挖掘的处理时间,因此评估了SHEMA算法的挖掘时间。图8是4个挖掘算法的时间与阈值δ的关系,MaHUSPM、MSPC与MHHUSP这3个算法的挖掘时间随着阈值的提高迅速提高,而SHEMA算法的增长速度慢于其它3个算法。 图8 不用阈值下的挖掘时间(Ta-Feng数据集, 模式长度=3) 图9 不用模式长度的挖掘时间(Ta-Feng数据集, δ=0.06045) 图9是4个挖掘算法的时间与模式长度的关系,MaHUSPM、MSPC与MHHUSP这3个算法的挖掘时间随着阈值的提高迅速提高,而SHEMA算法的增长速度慢于其它3个算法。主要原因在于SHEMA算法在1-项集与2-项集阶段设计了深度的剪枝策略,有效地抑制了候选模式的保留量。 大数据是高效用项集挖掘的主要应用场景,因此评估挖掘算法对于大数据集的可扩展性效果。统计4个挖掘算法对于Kosarak数据集的扩展性,图10是不同序列数量的挖掘时间曲线,MaHUSPM与MSPC算法的挖掘时间随着序列数量的增加而迅速提高,MHHUSP与SHEMA算法则随着序列数量的提高基本保持稳定,SHEMA算法由于采用了分布式挖掘的机制,其挖掘时间保持了较好的稳定性。 图10 不同序列数量的挖掘时间曲线(Kosarak数据集, δ=0.0045) 图11 不同阈值的挖掘时间曲线(序列数量=990 000) 图11是不同阈值的挖掘时间曲线,MaHUSPM、MSPC与MHHUSP算法的挖掘时间受阈值的影响较大,而SHEMA算法设计了深度的剪枝策略,实现了较为稳定的挖掘时间。SHEMA算法随着阈值的变化呈现较为稳定的趋势,具有较好的可扩展能力。 在项集的挖掘过程中需要缓存大量的候选项集,该过程需要消耗大量的内存资源,因此挖掘算法的内存成本也是挖掘算法的一个重要性能指标。图12是不同序列数量挖掘过程所需的内存容量,MaHUSPM与MSPC算法的内存消耗随着序列数量的增加而迅速提高,MHHUSP与SHEMA算法则随着序列数量的提高基本保持稳定,可获得结论MHHUSP与SHEMA算法的剪枝效果较好,避免了大量的候选项集缓存。 图12 不同序列数量挖掘过程所需的内存容量 (阈值为3%) 图13是不同阈值挖掘的内存消耗曲线,MaHUSPM算法的内存消耗受阈值的影响较大,MSPC与MHHUSP而SHEMA算法则实现了较为稳定的内存消耗曲线。SHEMA算法设计了深度的剪枝策略,实现了较低的内存消耗结果。 图13 不同阈值的内存消耗(序列数量=9.9×105) 算法在评估前缀树节点的过程中,各个节点的挖掘顺序独立于其它的同级节点,所以可以并行地处理前缀树中的所有子节点,并且不会影响结果。据此给出了本算法的分布式实现方案,能够在云计算、GPU(graphics proces-sing unit)、多核处理器等平台上实现并行计算。SHEMA算法设计了深度的剪枝策略,实现了较为稳定的挖掘时间。SHEMA算法随着阈值的变化呈现较为稳定的趋势,具有较好的可扩展能力与稳定性。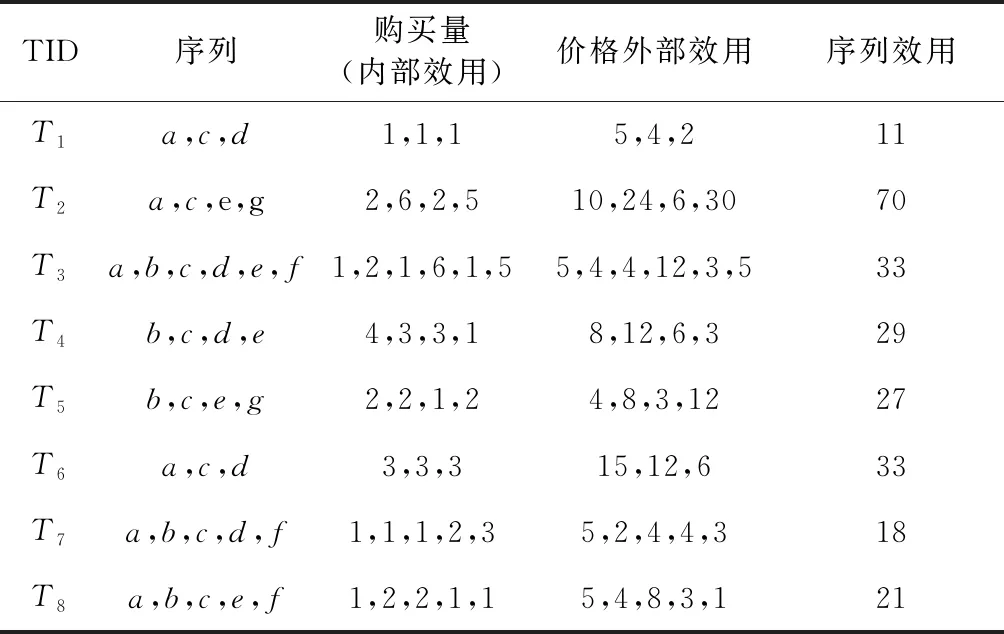

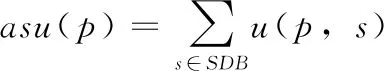
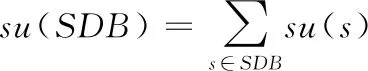

2 数据结构与算法设计
2.1 会话序列的字典树(前缀树)结构
2.2 基于数组的低内存快速挖掘策略

2.3 索引效用列表

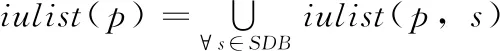
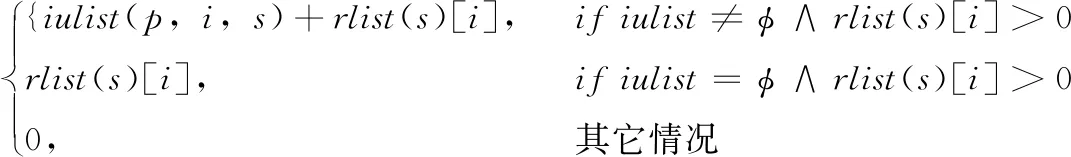
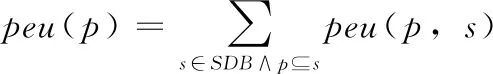
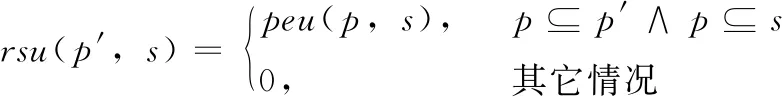

2.4 生成序列的iulist


2.5 效用上限与初步剪枝策略
2.6 串型高效用模式挖掘算法(string high efficient pattern mining algorithm,SHEPMA)
3 分布式高效用模式挖掘算法(distributed high efficient pattern mining algorithm,SHEMA)
3.1 分布式效用列表设计
3.2 分布式多阈值挖掘的深度剪枝属性
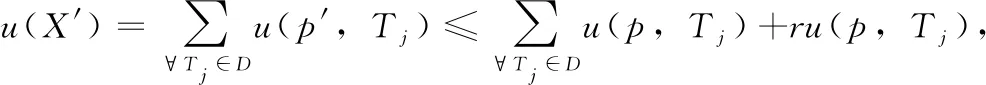
3.3 SHEMA算法
3.4 SHEMA的分布式实现方案
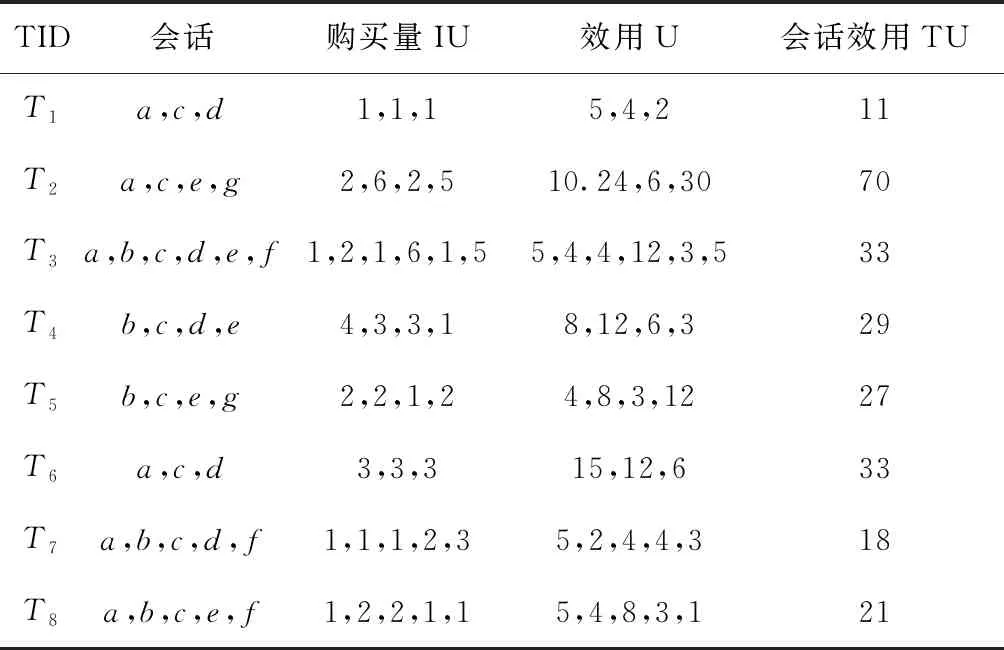
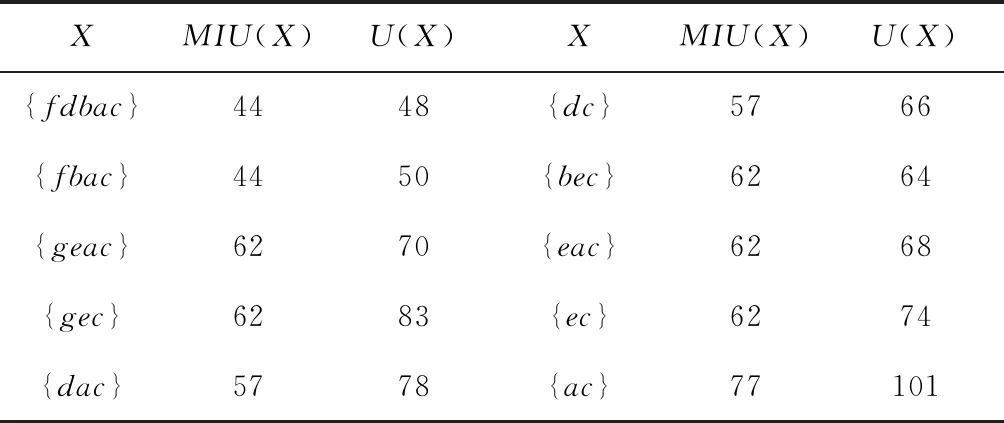
3.5 算 例

4 实验结果与分析
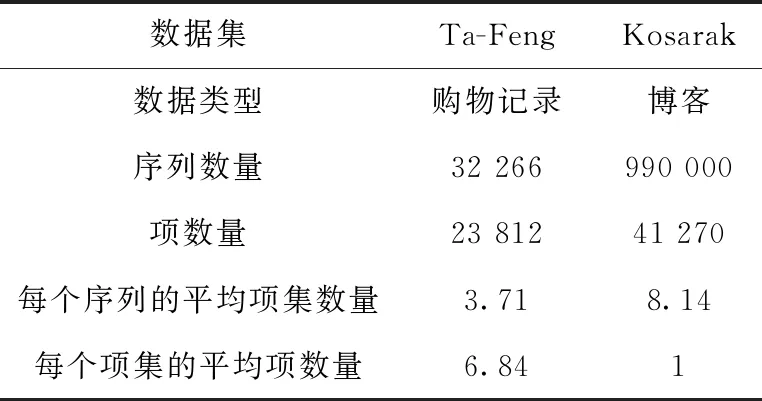
4.1 实验数据集
4.2 剪枝策略的性能
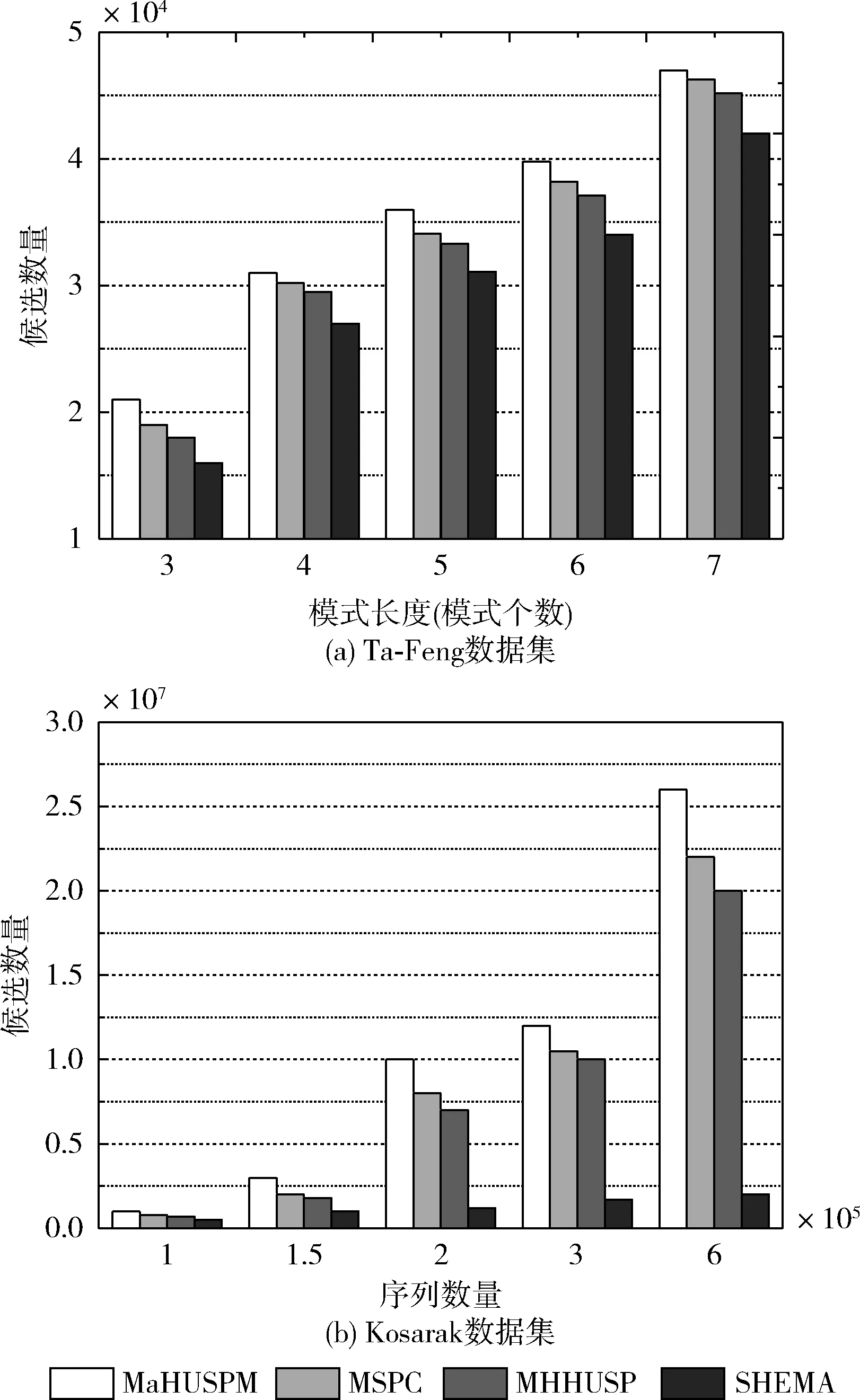
4.3 挖掘算法的挖掘时间

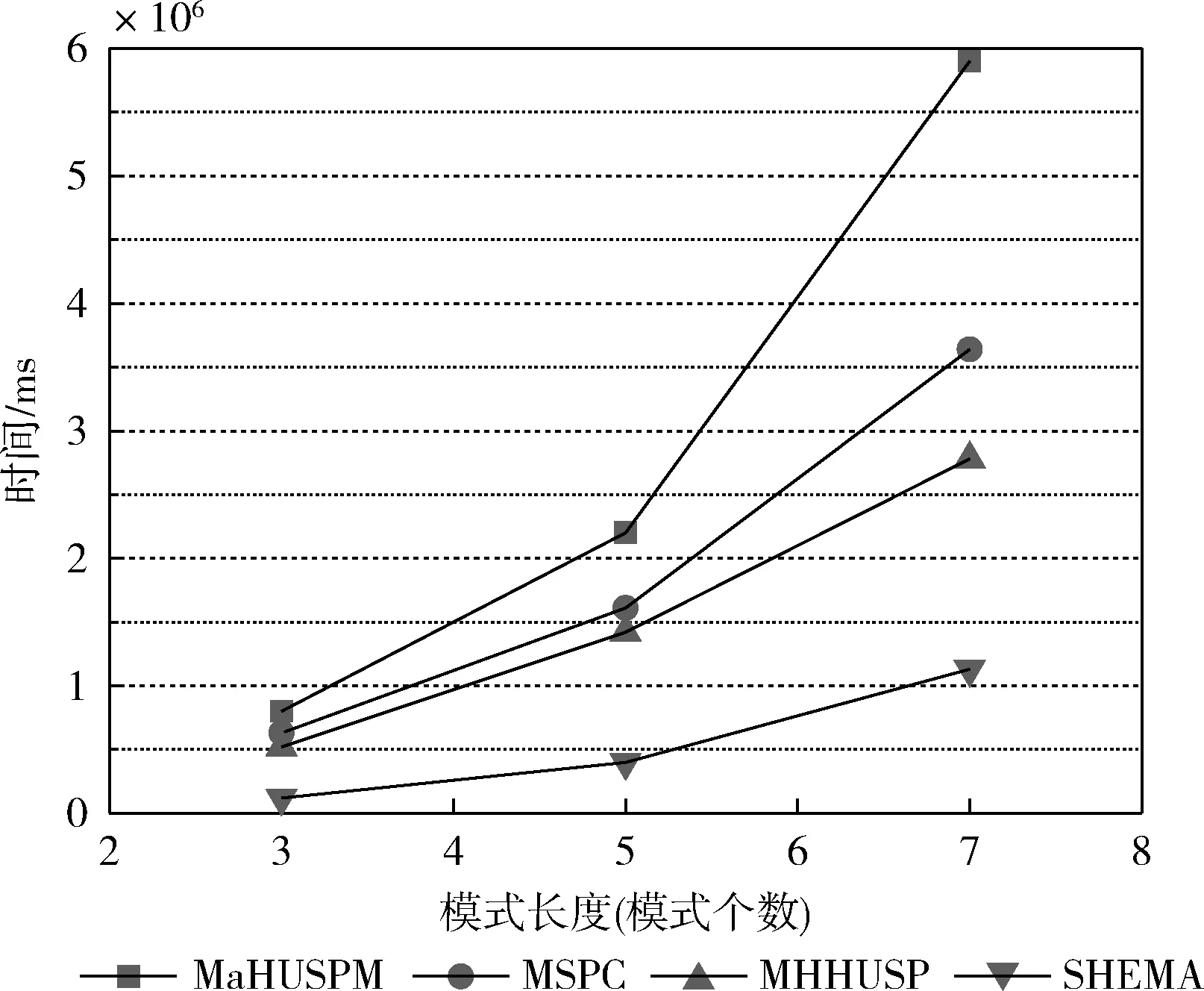
4.4 挖掘算法的扩展性性能

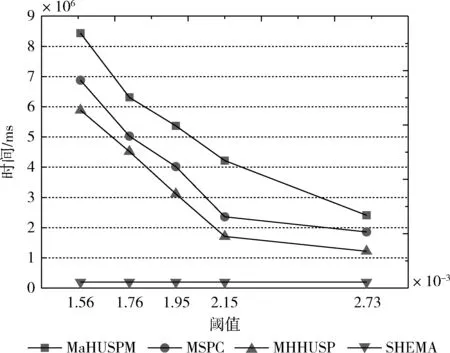
4.5 挖掘算法消耗的内存

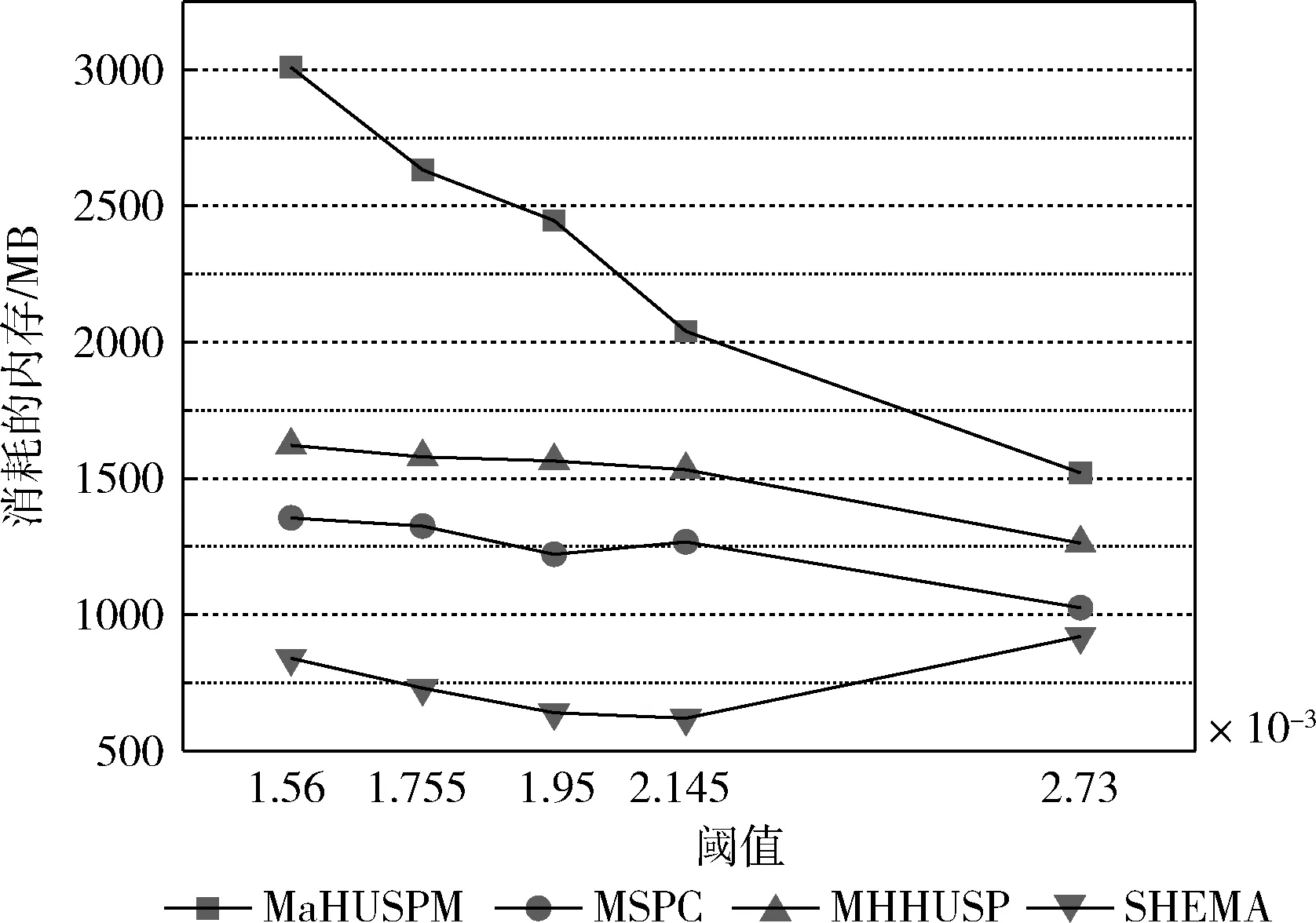
5 结束语

