改进灰狼算法及其应用

袁 岩，曹萃文

(华东理工大学 化工过程先进控制和优化技术教育部重点实验室，上海 200237)

0 引 言

群体生物有各自独特的群体规律性，学者们根据这些规律发掘出众多群智能优化算法[1-3]。这些算法常被应用于复杂数学求解问题[4，5]和实际工程建模优化[6-8]问题，并取得了很好的效果。灰狼算法[9](grey wolf optimizer，GWO)作为新型的仿生智能优化算法之一，因其算法结构清晰、灵活，调节参数较少，寻优精度相对较高等优点被许多研究学者广泛采用。为进一步提升灰狼算法的性能，文献[10]提出了基于末尾探索者策略的改进灰狼算法，此算法提升了算法规避局部最优的能力；文献[11]提出了基于贪婪思想和变异策略的改进灰狼算法，此算法提升了标准灰狼算法开发能力不足的问题。以上提出的两种改进方式都在一定程度上解决标准灰狼算法的全局勘探开发能力，但是以上改进的两种方式中位置更新策略和标准灰狼算法的位置更新策略大致相同，仍然存在容易陷入局部最优解的可能，算法的开发能力还有提升的空间。

针对以上问题，提出了一种改进的多策略灰狼算法(multi-strategy grey wolf optimizer，MSGWO)。MSGWO算法在标准GWO算法基础上，在算法初始化阶段加入对立搜索策略，在迭代计算过程中引入正弦余弦搜索策略和自适应局部搜索策略，加强算法全局探索开发能力、收敛速度和寻优精度。最后将MSGWO算法应用于8个测试函数的求解问题和加氢裂化数据建模参数的优化问题，对该算法的有效性和实际工程应用效果进行验证。

1 灰狼算法

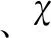
(1)包围猎物

当狼群发现猎物时，灰狼会迅速向猎物前进，其灰狼的位置更新及灰狼与猎物的距离如式(1)-式(3)描述(设搜索空间为d维)

X(t)={Xi(t)|i=1,2,…,d}

(1)

(2)

X(t+1)=XP(t)-AD

(3)

其中，t表示当前迭代次数，X(t)表示第t代灰狼的位置向量，D表示灰狼与猎物间的距离向量，XP(t)表示第t代猎物的位置向量(用当前种群的当前最优解代入)，C和A为系数变量，分别由式(5)和式(6)计算得到

(4)

C=2r2

(5)

A=2ar1-a

(6)

其中，a在迭代过程中按式(4)线性从2降到0，max_it为最大迭代次数，r1和r2为[0,1]上均匀分布的随机数。

(2)追捕猎物

当狼群包围猎物以后，狩猎行为开始，根据适应度排序得到最优解Xα、次优解Xβ和当前第三优解Xδ。其中α、β、δ灰狼的位置更新如式(8)，剩下灰狼的位置更新受到α、β、δ灰狼的引导，其更新方式如式(9)所述

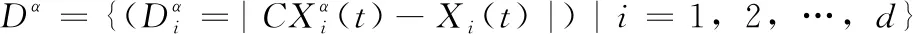
(7)

X1=Xα-ADαX2=Xβ-ADβX3=Xδ-ADδ

(8)

(9)

(3)攻击猎物

如上所述，待猎物停止移动时，灰狼开始攻击猎物。此过程可用数学描述为，A为[-a,a]之间的一个随机值，当A的值在[-1,1]范围之外时，搜索代理可以在灰狼当前位置和猎物位置之间的任意位置进行局部搜索，当A的值在[-1,1]范围之内时，灰狼必须攻击猎物。

2 改进的灰狼算法

2.1 对立搜索策略

GWO算法初始化种群位置采用的是随机初始化的方式，随机初始化种群个体位置有可能导致可行解的搜索范围变大，搜索时间延长，搜索速度较慢等缺点，进而影响整个算法的收敛速度。

本文在随机初始化的基础上添加对立搜索策略，其基本思想是在随机初始化的种群个体时，产生其对立个体，并将对立个体和此随机初始化个体进行适应度评价对比，当对立个体适应度评价优于此个体时就采用此个体，否则使用随机初始化的个体。数学表达式如下

(10)

其中，Ub、Lb为X的上下界，X(0)为初始化位置向量

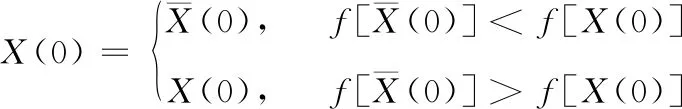
(11)

2.2 正弦余弦搜索策略

在GWO算法中，狼群的位置更新主要受到α、β、δ灰狼的引导，为提高GWO算法搜索精度，本文引入Seyedali Mirjalili的正余弦搜索算法[12]。即狼群在α、β、δ灰狼按式(9)的引导进行位置更新之后，再进行一次正弦余弦搜索。正弦余弦搜索的数学表达式如下

(12)

(13)

(14)

r4∈(0,360°)

(15)

式中：r3随迭代次数的增加而自适应减少，a为常数此处取值为2。r5，r6为[0,1]上的均匀分布的随机数。正余弦交叉搜索策略可以防止算法早熟从而提高算法的寻优精度。

2.3 自适应局部搜索策略

为提高GWO算法规避局部最优的能力，提出自适应局部搜索策略。GWO算法将α狼的位置作为算法的最优解，加入自适应局部搜索策略后，对最优位置Xα进行局部搜索，即在最优位置进行邻域搜索。最后将得到的新的最优解的邻域值与最优解逐个进行适应度比较，选取适应度好的个体作为新的最优解。

在迭代更新过程中，邻域搜索范围也会随迭代次数逐渐缩小，平衡了搜索速度和寻优精度，达到自适应搜索的目的，其数学表达式如式(16)描述

Xα(t+1)=(1-ε)Xα(t)+εRand

(16)

式中：ε为自适应系数，其元素值由式(17)决定

(17)

其中，Rand为d维的向量,其向量元素值为[0,1]上的均匀分布的随机数。

2.4 MSGWO算法流程

MSGWO算法的计算步骤如下：

(1)设置种群规模、最大迭代次数、待优化问题维度；

(2)初始化种群位置，对随机初始化位置进行对立搜索计算，比较随机初始值和对立值的适应度值，选取适应度好的种群个体作为初始化种群；

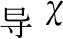
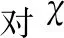
(5)对狼群个体进行适应度排序得到最优个体，对最优个体位置进行一次局部自适应搜索，并计算其适应度与最优值进行比较，选取适应度好的解作为新的最优个体；

(6)判断运算结果是否满足终止条件，满足则算法结束，否则转至步骤(2)。

3 实验测试与分析

3.1 实验测试

为检验改进后的灰狼算法性能，选取表1中的8个标准测试函数进行测试。仿真实验采用的计算机配置详细情况为：CPU为Intel Core i7-8550U，主频为2.0 GHz，16 G RAM，操作系统为Microsoft Windows10 64位操作系统。计算环境为Matlab2017(b)。实验测试中为检验改进算法对不同维度问题的处理能力，依次对表1中的8个测试函数分别进行20、30、50维测试。首先将MSGWO算法测试结果与GWO算法测试结果对比分析如图1中的8个收敛曲线图所示。然后将MSGWO算法和粒子群算法(particle swarm，optimization，PSO)、人工蜂群算法(artificial bee colony，ABC)、改进人工蜂群算法(improved artificial bee colony，I-ABC)对比分析，算法寻优求解结果使用求解平均值(Mean)和标准差(Std)作为对比指标在表2中展示，其中ABC、I-ABC算法中的数据源自文献[13]。

表1 无约束测试函数

为客观公正评价算法的性能，对算法选取以下的参数设置：4个算法种群规模均设置为40，最大40 000次适应度评价，分别独立运行50次取平均值。运行结果见表2，黑体加粗数据表示MSGWO算法较GWO算法寻优结果更好。

3.2 实验分析

(1)由表2可以看出，MSGWO算法相比较GWO算法对8个测试函数在20、30、50维寻得7次最优，尤其对f1、f2、f3、f6、f8测试函数寻优时，寻优精度提升明显，说明改进后的算法是有效的。表2数据显示，在测试函数高维(50维)寻优求解时，MSGWO算法同样表现出色。

(2)标准差用于反映算法求解寻优的稳定性，由表2的标准差列数据对比可以看出，MSGWO算法对8个测试函数的标准差值7次小于GWO算法，说明MSGWO算法的稳定性较好。

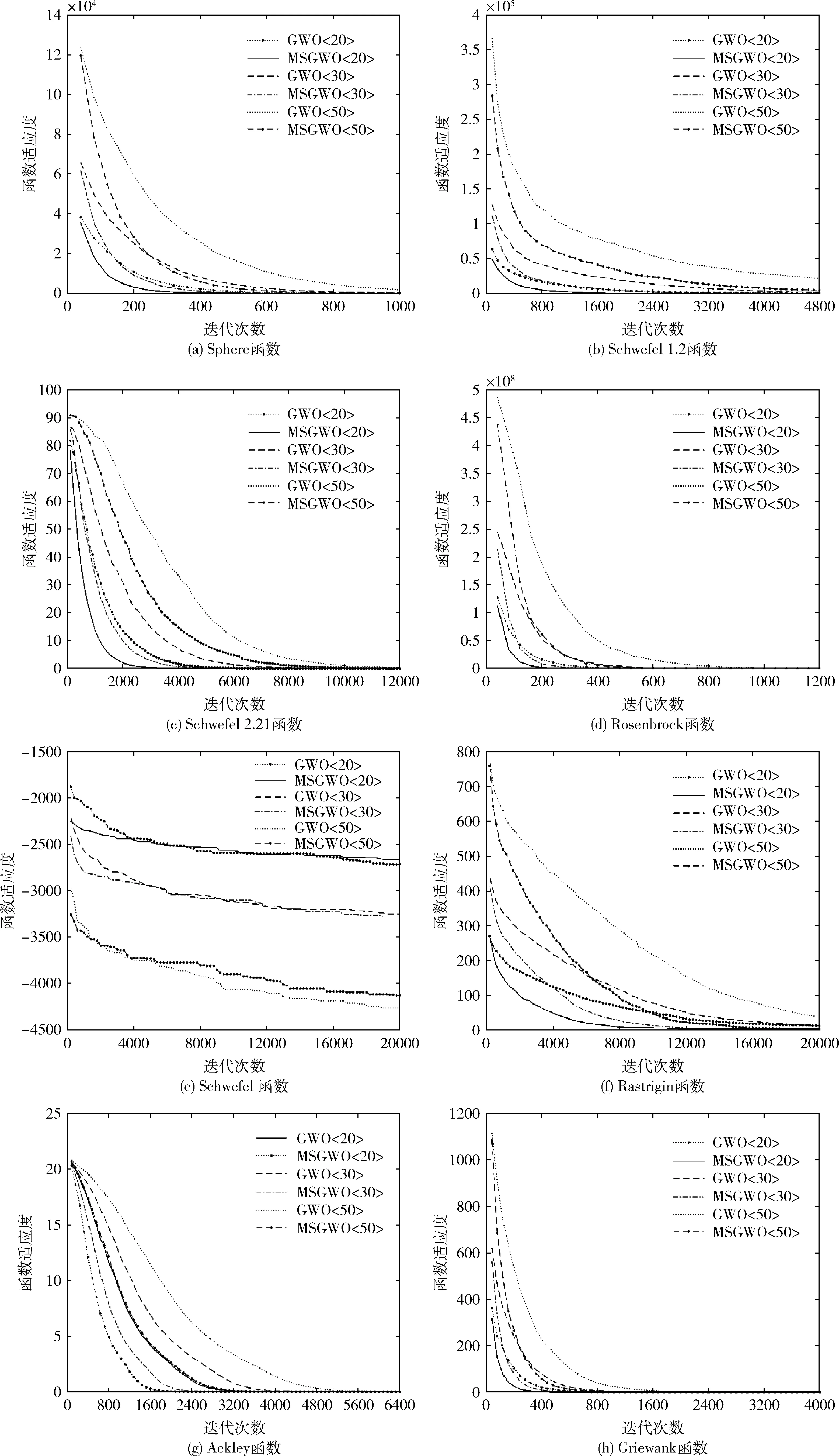
图1 测试函数的收敛效果

(3)图1中8个收敛曲线图显示，对于8个测试函数的20维、30维、50维等3个不同维度上的求解计算，MSGWO 算法收敛速度均快于GWO算法的收敛速度，表明MSGWO算法的收敛速度较快，改进效果很好。

(4)表2可以得到，MSGWO算法对Rastrigin、Griewank两个测试函数取得全局最优值，对于测试函数Schwefel，GWO算法求解时易陷入局部最优，而MSGWO算法能够跳出局部最优更接近理论最优值，说明改进灰狼算法采用局部自适应搜索策略能够一定程度上规避局部最优解，从而提升算法的全局勘探开发能力。

4 算法实例研究

4.1 最小二乘支持向量机

支持向量机(support vector machine，SVM)是一种二分类算法模型，采用最大间隔的学习策略，是数据驱动建模技术中的一种重要方法。最小二支持向量机(least squares support vector machine，LSSVM)是SVM的改进，把SVM中的优化约束中的不等式约束转化为等式约束问题，避免了求解二次规划问题，降低了计算复杂性，使得易于实际应用和大规模的数据建模场景。LSSVM优化问题的数学描述为：

设有n个样本组成的样本训练集

T={(xk,yk)|xk∈Rn,yk∈R,k=1,2,…,n}

(18)

其中，xk为输出向量，yk为输出变量。

可以构造一个分类函数

y(x)=wTφ(x)+b

(19)

其中，b为偏置变量，φ(·)∶Rn→Rnk为非线性映射函数，即将原输入特征空间映射到一个高维特征空间，w∈Rnk为权重系数向量。

那么LSSVM的最优化目标问题可以表述为

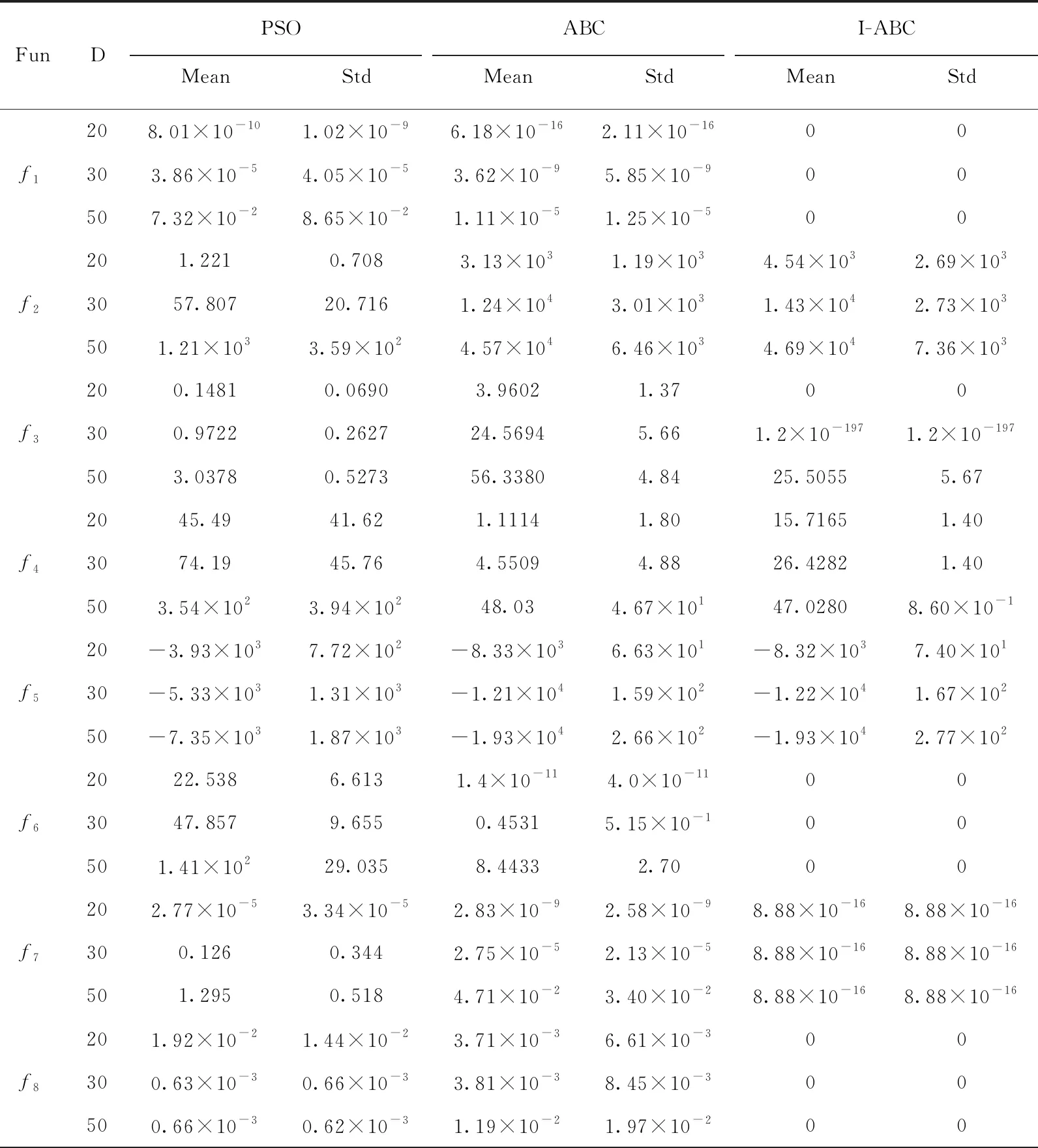
表2 算法优化对比结果

表2(续)

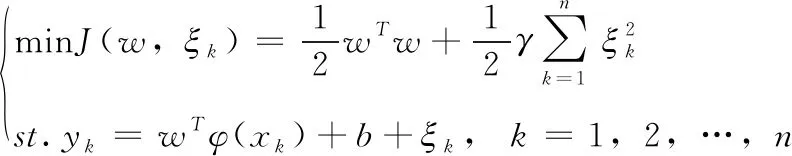
(20)

为解决该最优化问题构建拉格朗日函数为

L(w,b,,k))

(21)

对其求偏导数，得到

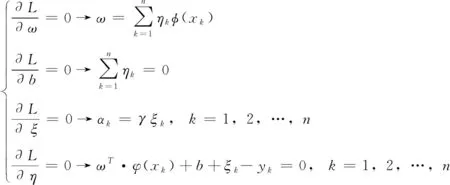
(22)

通过引入核函数

K(xk,xl)=φ(xk)·φ(xl),k,l=1,2,…,n

(23)

扩展到非线性领域，可获得线性方程组

(24)

通过上式，可以求得LSSVM的模型

(25)

其中本文中选用的函数为高斯径向基核函数

(26)

4.2 数据建模输入输出变量设计

单段串联加氢裂化工艺原理：原料油与氢气经加热炉后进入加氢精制反应器、加氢裂化反应器进行加氢精致、加氢裂化反应。反应产物降温后经热高压分离器后进入冷高压分离器进行油、水、气三相分离。冷高压分离器底部的生成油经减压后送入低压分离器，其流出物进入汽提塔，塔底流出物经加热后送入分馏塔，得到轻石脑油、重石脑油、航空煤油、柴油以及渣油[14,15]。

根据加氢裂化工艺原理以及使用Aspen Hysys模拟加氢裂化工艺流程灵敏度分析，得到影响加氢裂化产品产量以及产品性质的主要操作条件是[16]：原料油流量、反应氢油比、反应空速、反应压力、新氢补充量、循环氢耗量、反应器1床层1温度、反应器1床层2温度、反应器2床层1温度、反应器2床层2温度，所以选取以上10个变量作为数据建模的输入变量。选取航空煤油产量、航空煤油硫含量、航空煤油氮含量、航空煤油烷烃量、柴油产量、柴油硫含量、柴油氮含量、柴油烷烃含量共计8个输出变量作为预测目标变量。

4.3 数据驱动建模及参数设计

实验数据为某炼油厂实际采集的288组数据，随机选取220组数据作为训练数据集，剩余68组数据作为测试数据集。为说明改进算法的有效性，本文在Matlab2017(b)环境下，构建以下5种预测模型：①BP神经网络预测模型；②RBF神经网络预测模型；③PSO-LSSVM预测模型；④GWO-LSSVM预测模型；⑤MSGWO-LSSVM预测模型等共5个加氢裂化装置产品预测模型。

建模过程中的参数设置为：BP神经网络学习率为0.1，神经网络训练次数为1000；为保证所建模型使用算法对比的公平性，PSO、GWO、MSGWO等优化算法种群数统一设置为40，算法迭代次数均设置为500次。

预测目标误差选择：误差评价指标选择平均绝对误差(mean absolute deviation，MAD)，相对平均百分误差(mean absolute percentage error，MAPE)和均方根误差(root mean square error，RMSE)，其计算方式分别如式(27)-式(29)所示

(27)

(28)

(29)

目标函数：待优化的LSSVM模型的参数为式(20)中惩罚因子γ， 以及式(26)中核参数σ， 参数区间设置为γ∈[0.01 500],σ∈[0.01 30]， 优化的目标函数为

(30)

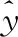
4.4 模型预测结果分析

PSO、GWO、MSGWO算法寻优γ和σ结果见表3。

表3 算法寻优γ和σ结果

本文选用MAPE和RMSE作为预测效果检验指标，预测结果见表4，黑体表示4种模型中结果最优值。其中表4中以“D_”开头表示柴油性质，以“J_”开头表示航煤油性质。预测效果如图2所示(为使图形清晰直观，程序中选取68组测试数据集中的前20组数据作图分析对比)。

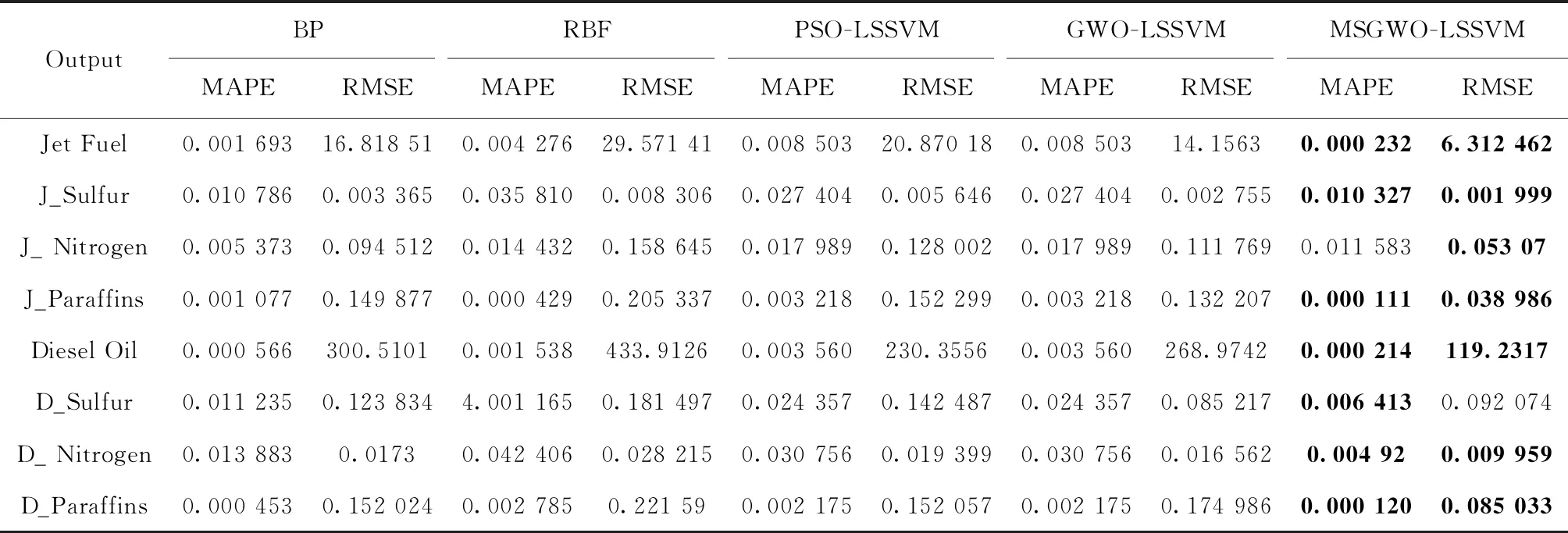
表4 5种预测模型预测对比结果

由表4和图2可以看出，相比较其它4种预测模型，对于8个预测目标变量在MAPE和RMSE两个指标上MSGWO-LSSVM模型的预测精度6次最好，在航煤油氮含量预测上MAPE指标不是最好但是和其它模型相比差距很小，

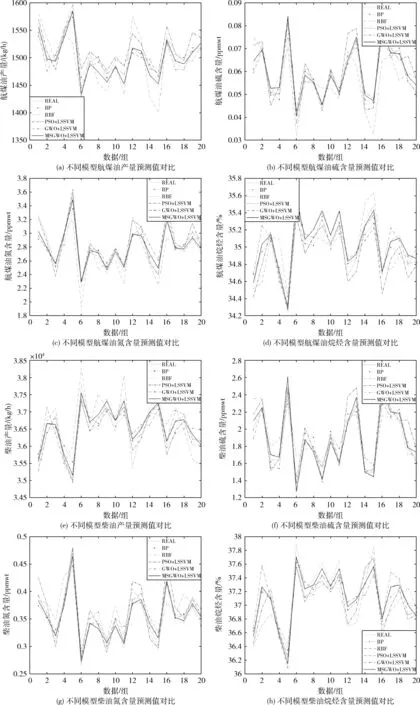
图2 各模型预测值对比

RMSE指标相对其它预测模型是最小的。在柴油硫含量预测上RMSE指标不是最好的，但是MAPE指标是最小的。说明所建MSGWO-LSSVM模型的预测效果是比较好的，具有一定的预测价值。这也进一步说明MSGWO算法在解决实际工程应用上的有效性和可行性。

5 结束语

本文针对GWO算法开发能力不足、收敛速度慢、易陷入局部最优等问题，提出了MSGWO算法，主要进行以下3个方面的改进：加入对立搜索策略进行种群位置初始化；加入正弦余弦搜索策略，提高算法的寻优精度和开发探索能力；加入自适应局部搜索策略，以提高算法的全局搜索能力防止陷入局部最优。使用8个Benchmark函数对MSGWO算法进行实验测试，并与GWO算法以及PSO、ABC、I-ABC算法进行比较，仿真实验结果表明，MSGWO算法在求解精度和收敛速度以及寻优稳定性上表现较好。

最后将MSGWO算法用于加氢裂化数据建模参数优化问题，建立MSGWO-LSSVM加氢裂化产品预测模型，并和其它4种预测模型对比分析，仿真结果说明MSGWO-LSSVM模型的预测精度较高，可靠性好。此模型可以较准确地预测出在操作工况条件变化下加氢裂化装置产品的产量以及产品性质，进一步验证了算法的有效性。