基于相关系数和灰色模型的振荡序列预测
田红丽,李成群,闫会强,陈 昕
(1.河北工业大学 人工智能与数据科学学院,天津 300130;2.河北工业大学 经济管理学院, 天津 300130;3.哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001)
0 引 言
灰色模型(grey model,GM)在振荡变化时间序列的预测研究一直是大家关注的热点问题,虽有很多研究成果呈现[1-4],但预测结果仍然不够理想。预测结果或导致病态结果出现,或得到的包络、区间形式,只能给出预测的大致区域。此外,现有的灰色模型在预测建模时,较少利用历史数据或完全舍弃历史数据[5,6]。实际上,随着数据的积累,振荡序列数据中的波动特性存在着一定的相似性。随着时间周期的积累,振荡序列也将呈现一定的周期性。
本文尝试充分利用历史数据信息,针对当前预测数据,利用本文提出的残差相关系数,在历史数据中寻找其相似数据段,在该相似数据段中利用遗传算法寻优得到灰色模型的权重系数。然后,利用最优权重系数灰色模型对当前数据进行预测,得到的预测结果再与历史数据结合,得到最终的预测结果。
1 基本理论
1.1 残差相关系数
文献[7]提出了一种综合考虑纵向偏差和横向残差的相关系数,相比其它相关系数可以更好地反映数据之间的相关性。但是该相关系数计算得到的相关系数数值普遍偏大,使得数据之间的区分性不明显。因此,本文提出一种新的残差相关系数(residual correlation coefficient,RCC)。该相关系数考虑了两个数据序列之间的空间距离及每个序列内横向残差之间的相似度。
给定两组数据X和Y, 它们之间的欧氏距离表示为
(1)
式中: T为转置运算符。
则二者之间的空间距离度量表示为
D(X,Y)=exp(-Δ(X,Y))
(2)
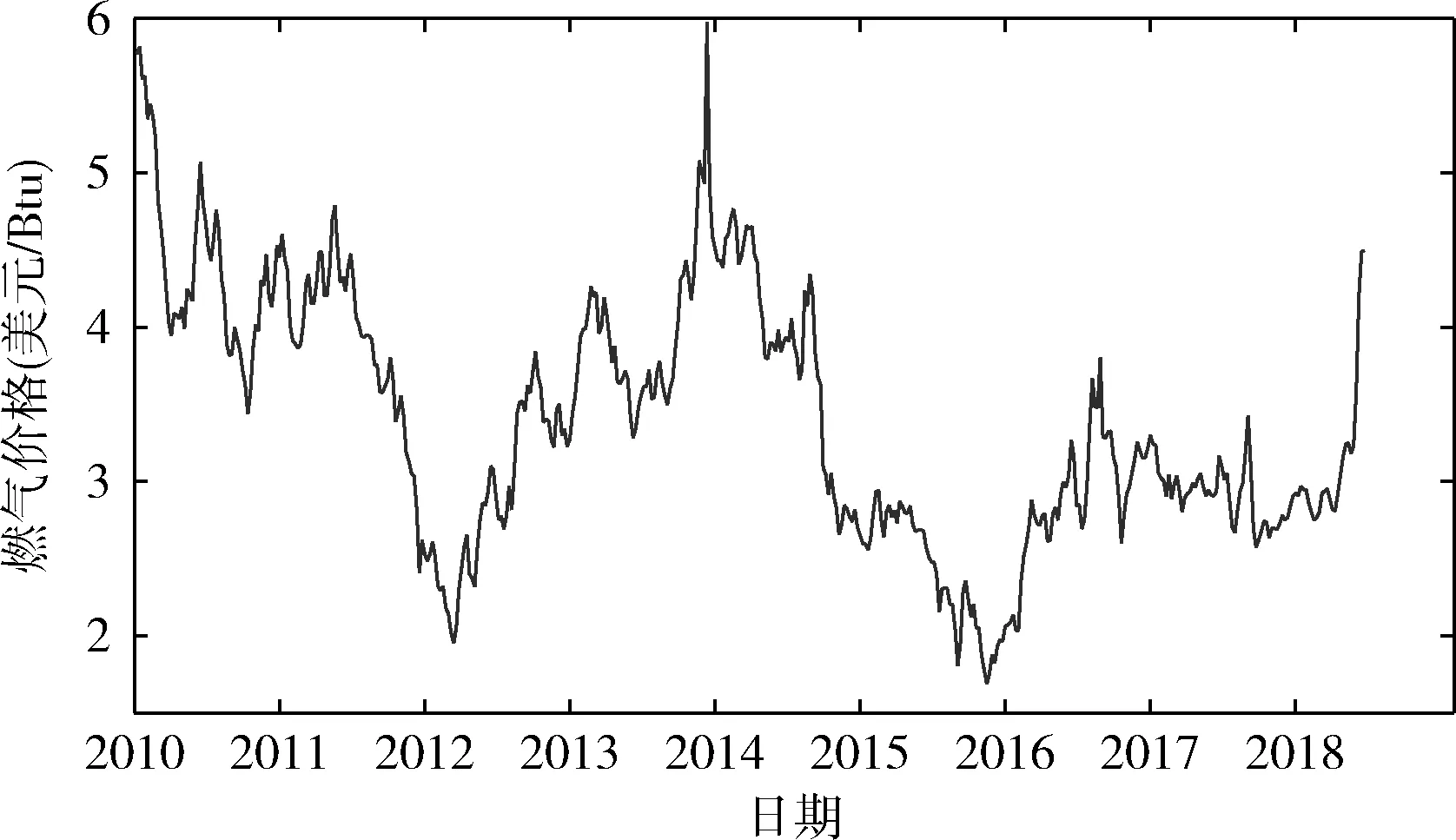
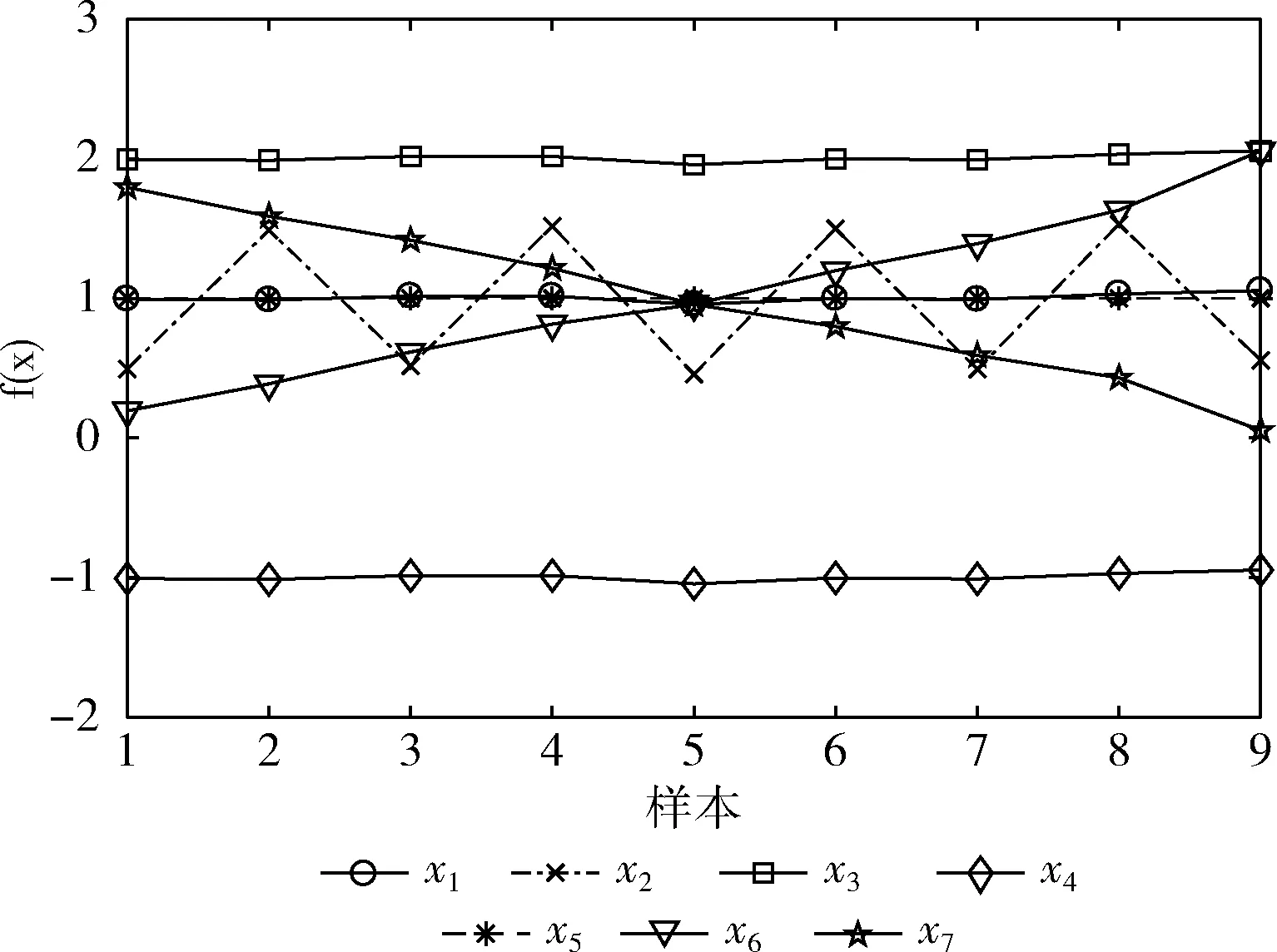
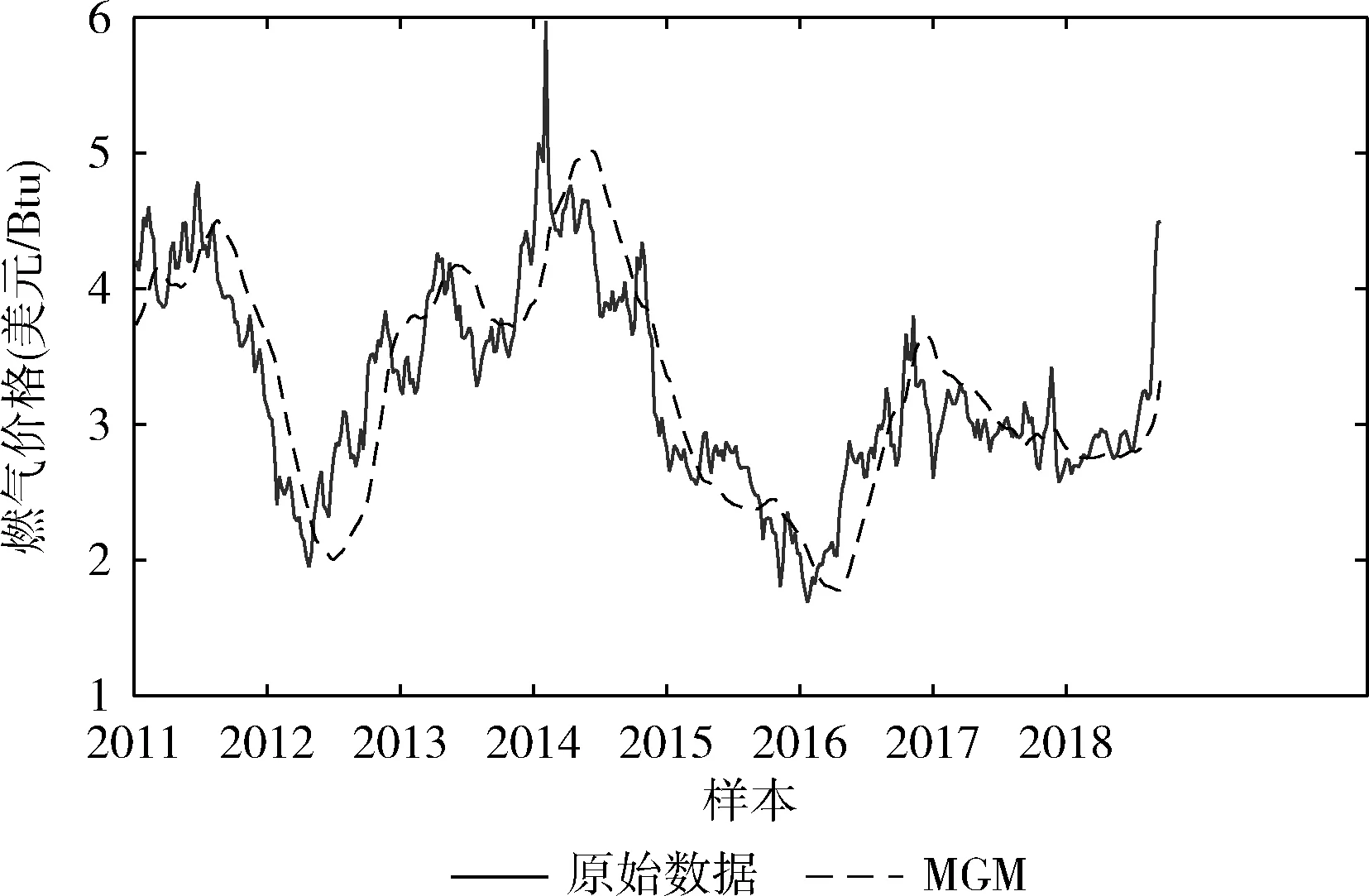
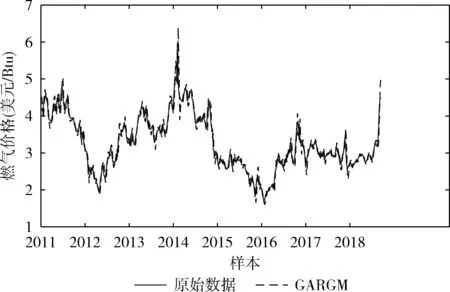
在式(2)中,利用指数运算可保证X和Y之间的距离呈现平稳过渡趋势,且0 在单一数据序列内,残差定义为 (3) (4) 因此,可以得到残差相关系数表示为 (5) 所以, 0 灰色预测模型是灰色系统理论的核心和基础,是一种客观的基于不确定性描述的预测模型。该模型巧妙地运用累加累减计算而放宽了对数据的苛刻要求,即该模型无需大量历史数据和数据序列的平稳性特征即可实现快速的中短期预测。但是,该模型及推广模型也普遍存在以下不足:①预测精度对模型参数选取比较敏感;②振荡数据的预测效果不理想。这也是本文主要解决的两个重点问题。 最常用的灰色预测模型为GM(1,1)模型。建立GM(1,1) 模型的基本流程和方法如下:给定X(0)={x(0)(1),x(0)(2),…,x(0)(t),…,x(0)(n)} 为一个时间序列模型,t=1,2,…,n,n称为历史数据维度。对其元素迭代累加后得到累加序列 X(1)={x(1)(1),x(1)(2),…,x(1)(T),…,x(1)(n)} (6) 由此得到紧邻加权值生成序列为 z(1)={z(1)(2),z(1)(3),…,z(1)(n)} (7) 式中:z(1)(k)=μx(1)(t-1)+(1-μ)x(1)(t),t≥2,μ为紧邻权重系数, 1>μ>0。 建立白化微分方程 x(0)(t)+az(1)(t)=u (8) 式中:a为发展系数,代表数据的发展态势;u为灰作用量,代表数据的不确定性。两个参数可按最小二乘法进行辨识获取 (9) 式中 (10) (11) (12) 则可解得离散时间响应函数为 (13) 然后利用累减运算求解预测结果为 x(0)(t+1)=x(1)(T+1)-x(1)(T) (14) 在最相似历史数据段Xh中,根据历史预测结果,以最小相对误差为目标函数,利用遗传算法寻找最佳的紧邻权重系数μ。 相对误差公式为 (15) 结合历史预测结果和当前预测结果,则可以得到最终的预测结果表示为 (16) 因此,可设计基于遗传算法寻优的组合预测模型一般过程如下: 步骤1 截取当前预测所需的训练数据序列Xc; 步骤2 在所有历史数据序列XA中,遍历计算每个等长序列与Xc的相关系数,找到具有最大相关系数的历史序列段Xh; 步骤3 在历史数据段Xh中,对紧邻权重系数μ通过选择、交叉、变异操作,在最大进化代数范围内找到使得相对误差最小的紧邻权重系数; 步骤4 利用最优紧邻权重系数对当前数据序列进行预测,包括累加序列生成、紧邻生成、白化微分方程参数求解、方程求解和累减运算输出结果; 步骤5 根据式(16)得到最终的预测结果。 为验证本文所提模型的有效性,选取美国天然气数据作为研究对象,截取2010年1月1日至2018年11月30日期间每周的天然气价格,单位为美元/Btu(British Thermal Unit)。原始数据如图1所示。 图1 天然气价格原始走势 通过图1可以看出,所使用的天然气数据序列为典型的振荡数据。 对比实验包括两部分,第一部分为残差相关系数的验证实验,第二部分为预测验证实验。在残差相关系数验证实验中,对比的相关系数包括余弦相似度(cosine similarity,CS)、广义雅可比相关系数(generalized Jaccarb coef-ficient,GJC)、皮尔逊相关系数(Pearson correlation coef-ficient,PCC)和横向残差与纵向相关系数(longitudinal and transverse correlation coefficient,LTCC)[7]。在预测验证中,选取的对比方法包括向前滚动灰色模型(forward rolling grey model,FRGM)[8]、新陈代谢灰色模型(metabolism grey model,MGM)[9]和改进灰色模型(revised grey model,RGM)[10]。其中,本文简记为GARGM(genetic algorithm based residual grey model)。 在本文的组合预测模型中,初始历史数据个数为60,当前历史数据个数n为10,遗传算法进化代数为100,初始种群数为100,二进制编码长度为10,交叉概率为0.6,变异概率为0.001,紧邻权重系数变化范围为0<μ<1。 3.2.1 相关系数对比实验 在本部分实验中,同样选取文献[7]中所用的人工数据作为测试对象,其分布如图2所示。 图2 人工数据走势 在计算相关系数时,以x1为参考基准,分别计算序列x2至x7与x1的相关系数。可以得到各种方法的相关系数结果见表1。 表1 相似灰色模型预测结果 3.2.2 预测对比实验 各种对比方法得到的预测结果如图3-图6所示,所得的平均相对误差见表2。 图3 FRGM预测结果 图4 MGM预测结果 图5 RGM预测结果 图3-图6的预测结果表明,向前滚动灰色预测模型由于不恰当地使用了历史数据,导致其预测结果只能大致跟踪数据的走势,但无法实现较为精准的预测;新陈代谢灰色模型通过舍弃历史数据对新数据进行更新,而得到了相对较好的趋势保持结果;改进的灰色模型,通过在历史数 图6 GARGM预测结果 FRGMMGMRGMGARGM平均相对误差18.182110.64115.10814.5900 据中寻找较优的训练数据维度,而实现了较好的预测效果;而图6中本文所提方法则通过合理地利用历史数据信息,使得预测结果与真实结果具有更好的贴合效果。表2中的平均相对误差结果再次验证了上述分析结果。 针对灰色模型在振荡序列中预测的不足,提出一种基于残差相关系数和灰色模型组合的预测方法。首先,根据时间序列特点,提出残差相关系数。然后,将残差相关系数和灰色模型结合,利用遗传算法对灰色模型参数进行寻优。最后,得到一种加权预测结果。基于人工数据的对比实验结果表明,残差相关系数更符合人们的自然认知,更适用于时间序列间的相似关系计算。基于天然气价格预测的对比实验结果表明,本文所提的组合预测方法预测精度更高,适用于振荡序列的预测。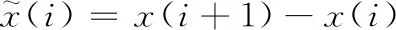

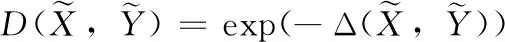
1.2 灰色预测模型

2 组合预测模型
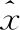

3 数值实验
3.1 数据来源及实验设定
3.2 对比实验与结果分析

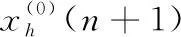



4 结束语

