Volterra型算子在Hardy空间和Bergman空间上的严格奇异性

林庆泽

（广东工业大学应用数学学院，广东 广州 510520）

0 引 言

用H（Δ）表示复平面单位圆盘Δ 上所有解析函数f 组成的函数空间，则Hardy 空间H2的定义如下：

用 A2表示 Δ 上满足

对于任一g∈H（Δ），定义Volterra 型算子Sg如下：

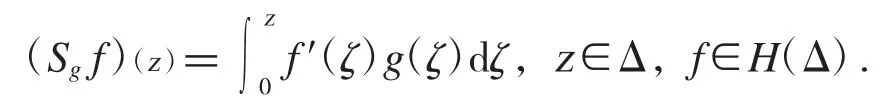
与Sg相伴而生的另一个算子是：

Pommerenke[1]首次研究Tg算子在Hardy 空间H2上的有界性并刻画了其与BMOA 函数的指数之间的联系.而关于Tg算子在一般的Hardy 空间Hp、Bergman Ap空间（0＜p＜∞）以及其它一些空间（包括加权Dirichlet 空间和加权Banach 空间等）上的有界性和紧性的刻画可参考文献[2-9].近年来，Miihkinen 等人[10-11]证明了Tg算子在Hardy 空间上的紧性与其严格奇异性的等价关系，其证明思路来源于文献[12].本文首先给出Sg算子在Hardy空间H2以及Bergman 空间A2上的有界性和紧性的充要条件，接着给出了Sg算子在这些空间上的严格奇异性的刻画，从而证明了该算子的紧性与其严格奇异性的等价关系.

1 Sg算子在Hardy 空间H2和Bergman空间A2上的有界性和紧性

我们首先给出Sg算子在Hardy 空间H2上的有界性和紧性的充要条件的完整刻画.记H∞为Δ 上所有有界解析函数f 组成的函数空间.根据Littlewood-Paley 不等式[13]，Hardy 空间H2有一个等价范数：

定理1若g∈H（Δ），则Sg算子在Hardy 空间H2上是有界的当且仅当g∈H∞.

证明若g∈H∞，则由Sg算子的定义可知，Sg算子在Hardy 空间H2上是有界的.

反过来，假设Sg算子在Hardy 空间H2上是有界的.由上面的Hardy 空间H2的等价范数可知，Sg算子在Hardy 空间H2上是有界的当且仅当存在C＞0 使得下面的不等式成立：

而根据文献[14]中的定理3.1，这个不等式成立当且仅当测度是一个3-Carleson 测度，根据文献[15]中关于Carleson 测度的等价条件的刻画，有下面的不等式成立：

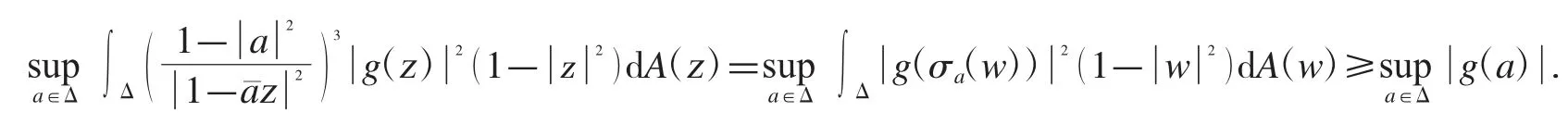
因此，g∈H∞.证毕.

定理2若g∈H（Δ），则Sg算子在Hardy 空间H2上是紧的当且仅当g≡0.

证明若g≡0，则很明显，Sg算子在Hardy 空间H2上是紧的.反过来，假设Sg算子在Hardy 空间H2上是紧的.同样根据文献[14]可知，Sg算子在Hardy 空间 H2上是紧的当且仅当测度是一个紧的3-Carleson 测度，也就是等于下面的极限[14]成立：

现在考虑Sg算子在Bergman 空间A2上的有界性和紧性条件.

定理3若g∈H（Δ），则Sg算子在Bergman 空间A2上是有界的当且仅当g∈H∞.

证明由于A2在范数意义上等价于加权Dirichlet 空间（参看文献[8]），因此 Sg算子在Bergman 空间 A2上是有界的当且仅当乘法算子（（Mgf）（z）＝g（z）f（z））在加权Bergman空间上是有界的[16-17]，而这又等价于g∈H∞.证毕.

定理4若g∈H（Δ），则Sg算子在Bergman 空间A2上是紧的当且仅当g≡0.

证明由与定理3 的证明思路一样.证毕.

2 Sg算子在Hardy 空间H2和Bergman空间A2上的严格奇异性

如果一个有界线性算子S:X→Y（其中X 和Y 是Banach 空间）限制在X 的任何一个无穷维闭子空间E 上所诱导出的线性算子SE:E→S（E）都不可能是同构映射，则称算子S:X→Y 为严格奇异的.类似地，如果一个有界线性算子S:X→Y（其中X 和Y 是Banach空间）限制在X 的任何一个同构于l2空间的无穷维闭子空间E 上所诱导出的线性算子SE:E→S（E）都不可能是同构映射，则称算子S:X→Y 为l2-奇异的[10-12].一个有界线性算子是紧的则必为严格奇异的，亦必为l2-奇异的；反之不然[12].

定理5若有界算子Sg在Hardy 空间H2上不是紧的，则Sg在Hardy 空间H2上不是l2-奇异的且Sg在Hardy 空间H2上不是严格奇异的.

换言之，定理5 是说，有界算子Sg在Hardy 空间H2上的紧性与其严格奇异性是等价的.

在证明定理5 之前，我们需要证明一个引理.由定理2 的证明可知，若Sg在Hardy空间H2上不是紧的，则存在Δ 内趋向于边界（不妨假定为1）的序列使得

也就是，存在k＞0 使得对于所有的an，都有其中容易验证，对于所有的

引理1若g∈H∞，对于Δ内趋向于1 的序列以及给定的ε＞0，定义集合记 m 为 Δ 的边界 ∂Δ的正则 Lebesgue 测度，则

证明（1）首先由几何关系，存在δ＞0 使得对于所有的n、0≤r≤1 以及都有不等式成立从而，

因此，对于任意的ζ∈∂ΔAε，都有

从而，

（2）当 ε →0 时，m（Aε）→0.由于 g∈H∞，算子 Sg是有界的，因此根据 Lebesgue 测度的绝对连续性，对于给定的证毕.

定理5 的证明 首先存在k＞0 使得对于所有的an，都有再由引理1，我们可以用归纳法得到，对于给定的序列ε1＞ε2＞…＞εn＞…＞0，我们能够找到序列的一个子序列使得下面三个不等式成立：

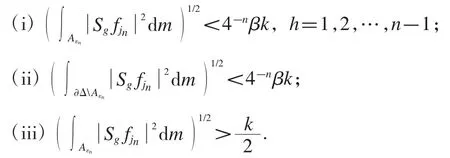
其中β 是一个充分小的正常数（其大小将在后面的证明过程中决定）.

接下来的按照文献[12]的617-618 页，我们得到，存在常数C1，C2＞0 使得对于任意的（bn）∈l2，都有若取g≡1，则可以推出存在常数C3，C4＞0 使得因此

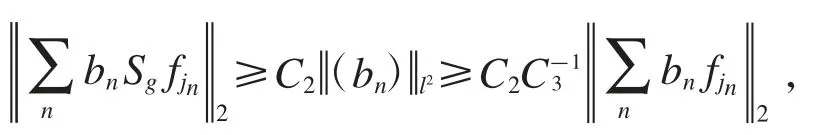
也就是，Sg在Hardy 空间H2上不是l2-奇异的，从而Sg在Hardy 空间H2上不是严格奇异的.因此，有界算子Sg的紧性与其严格奇异性是等价的.证毕.

定理6有界算子Sg在Bergman 空间A2上的紧性、l2-奇异性以及严格奇异性是两两相互等价的.

证明这是因为A2≈l2，可参照文献[12]的625 页.证毕.