工字型索网的几何与力集成设计方法①

陈聪聪，李团结*，唐雅琼，李欢笑

(1.西安电子科技大学，西安 710071；2.中国空间技术研究院西安分院，西安 710000)

0 引言

星载天线作为接收和反射电磁信号的载体，是实现深空探测、卫星导航、卫星通讯及电子侦察等任务的关键设备。为实现信号的远距离传输及获取微小发射功率的信号，星载天线需具有较大的口径；同时，受火箭运载能力和运载空间的限制，星载天线必须质量轻且为可展开的形式。美国航空航天局(NASA)、俄罗斯宇航局、欧空局(ESA)、日本宇航科学研究所(JAXA)及中国空间技术研究院等科研机构对各种类型的可展开天线进行了相关研究。如图1所示，根据结构形式的不同，空间可展开天线可分为固面可展开天线、充气式可展开天线、半刚性可展开天线及索网反射面可展开天线等[1-3]。

(a) 固面可展开天线 (b) 充气式可展开天线

目前，在轨运行的大口径天线主要为索网反射面天线。如图1. (d)所示，该类天线主要由可展开支撑结构、索网系统和金属丝网三部分构成。在支撑结构的作用下，索网系统张成特定形状的反射面，金属丝网依附于索网系统上，实现电磁信号的反射与接收。为保证电磁波能够有效的聚集，天线反射面的形面精度需有效保证。

由于索网系统不存在稳定的无应力状态，需要施加一定的预张力才能使其张成满足工作需求的形状并具有一定的承载刚度。现有天线反射面设计方法主要有两种：一是节点与预张力分步设计方法，即首先根据一定的形面精度要求设计网面节点的几何位置，然后寻求一组可使网面节点保持在设计位置的平衡预张力，常用的预张力设计方法有非线性有限元法、极小二范数、动力松弛法、逆迭代算法等；二是节点与预张力耦合设计方法，即利用张力与几何的耦合关系实现索网的几何设计的方法，常用的有Linkwitz和Schek等人[4]提出的力密度法及其演变方法[5]。

天线索网系统的几何形状和预张力相互牵制、相互耦合。一方面，当预张力设计不合理时，往往会造成一定的网面误差，影响天线精度；另一方面，当几何结构设计不合理时，又会造成预张力的不均匀，影响反射面的稳定性，甚至出现不存在使节点平衡的解的情况。

伞型索网反射面可展开天线(如图2所示)结构简单可靠，反射面精度好，在我国成功应用于多个型号中。本文针对伞型天线中广泛应用的工字型索网[6](如图3所示)，提出一种几何与力集成设计方法，该方法可有效控制背网面的张力水平且不受反射面及边界条件对称性的限制，具有较好的通用性。

图2 嫦娥四号月球探测器中继卫星Fig.2 Relay satellite of Chang'e-4 lunar probe

图3 工字型索网结构示意图Fig.3 A schematic of I-shaped cable net structure

1 工字型索网几何与力集成设计方法

1.1 工字型索网节点力平衡条件

单片工字型索网如图4所示。为保证反射面的形面精度，前网面的节点均位于理想反射面上；张力阵与背网面共同作用为前网面成形提供必要的张力；边界节点为索网与可展开支撑结构的连接点。

图4 单片工字型索网Fig.4 Single I-shaped cable net

索网上某节点i的力平衡方程为：

(1)

其中：Tij为索段的张力；lij为索段长度；j为与节点i相连的节点；(xi,yi,zi)，(xj,yj,zj)分别为节点i和节点j的坐标值；fix,fiy,fiz为节点在x,y,z方向所受外力；ci为与节点i相连的索单元数。对于索网中的自由节点，当其处于平衡状态时所受外力为0，即fix=fiy=fiz=0。对于拓扑形状已经确定的索网结构，当其在不受外载荷作用达到自平衡状态时，结构中所有非约束节点的力平衡方程是一个齐次线性方程组：

MT=0

(2)

其中：M为节点力平衡方程的系数矩阵，由索网节点位置和节点间连接关系唯一确定；T是索单元的张力向量。

对于平面工字型索网结构，当前网面分段数为N时，整个索网的约束方程数为4(N-1)(前、背网面各N-1个自由节点，每个节点X,Y方向分别受力平衡)，未知索力数为3N-1，当N>3时，未知变量数小于约束方程数，此时，节点平衡方程可能无解，即不能求得适当的索力值，使网面的所有节点均取得平衡。

特别的，对于边界条件对称的工字型索网(四个边界节点位于矩形的四个角点上)，可直接将前网面节点及张力进行对称得到背网面节点及张力[7]。对于边界条件不对称的索网，多采用不断迭代背网面节点坐标的方式，寻找一组存在平衡张力的节点位置[8]。上述方法均可得到满足一定精度要求的节点坐标及平衡张力，但未考虑背网张力值水平。

为此，提出一种可直接考虑背网张力水平的工字型索网几何与力集成设计方法。

1.2 背网面节点坐标及张力计算

如图5所示，背网面上节点i的坐标为Si=(xi,yi,zi)，与其相连的三个节点分别为ui,i-1,i+1。

图5 背网面坐标及张力求解示意图Fig.5 Solution diagram of coordinates and pretensions of back net

为使节点i平衡，则节点i、i-1、i+1、ui必须在同一平面上，该平面的方程为：

n(x-xi)+m(y-yi)+p(z-zi)=0

(3)

其中，(n,m,p)为平面的方向向量，可利用式(4)求解。

(n,m,p)=(xui-xi,yui-y,zui-zi)×

(xi-1-xi,yi-1-yi,zi-1-zi)

(4)

节点i+1的坐标Si+1为节点i,i-1,ui坐标Si、Sui、Si+1的函数，即：

Si+1=G(Si-1,Si,Sui)

(5)

节点i的平衡方程为：

fi+fi+1+fui=0

(6)

其中，fi,fui,fi+1是图中对应索段的张力向量，其大小分别fi,fui,fi+1。索力fi+1为索力fi,fui的函数：

fi+1=F(fi,fui)

(7)

所以，平衡时背网面节点坐标为前网面节点坐标和背网面第一根索张力的单值函数。

1.3 工字型索网几何与力集成设计方法

对于xoy平面内，张力阵沿y方向的平面工字型索网，若要求前网面节点位置不变，则根据平面投影原理，给定前网面张力沿水平方向的分量F1x，前网面和张力阵中的张力将唯一确定。

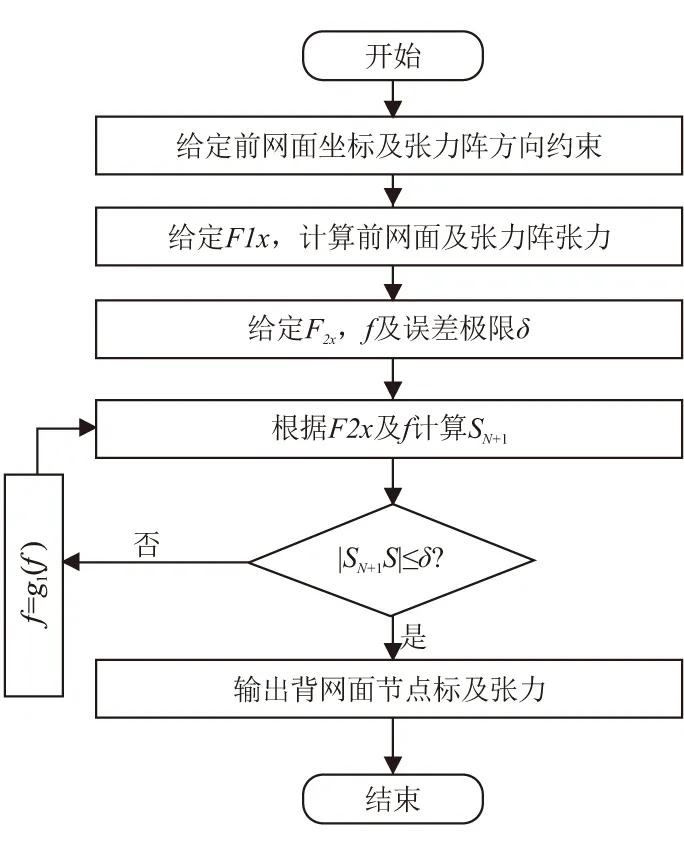
图6 平面工字型索网迭代求解流程图Fig.6 Flow chart of iterative algorithm of planar I-shaped cable net

稍加改进，上述方法可推广至前网面具有一定垂度的空间工字型索网的几何与预张力设计中。由于金属丝网张力等因素的影响，反射面边界处的索网往往具有一定的垂度。网面设计过程中要求前网面节点位于理想反射面上且位置保持不变，张力阵在xoy面内的投影平行于y轴。采用嵌套迭代的方式进行求解，具体流程如图7所示。

图7 空间工字型索网迭代求解流程图Fig.7 Flow chart of iterative algorithm of spatial I-shaped cable net

2 算例验证

对于图8所示的平面工字型索网，其前网面分为8段，张力阵沿竖直方向，图中各节点坐标如表1所示。

图8 工字型索网节点编号Fig.8 Node number of I-shaped cable net

表1 平面工字型索网各节点坐标Table 1 Node coordinates of planar I-shaped cable net

给定前网面张力的水平分量为10N，背网面张力水平分量为20N，算法迭代极限误差为1×10-13，用进退法进行迭代求解。如图9所示，经过361步迭代，算法收敛，迭代总用时0.0275s。给定不同的背网面张力水平分量值，设计结果如图10所示，可见，本文所提方法可很好的控制背网面的张力水平。

图9 算法迭代曲线Fig.9 Algorithm iteration curve

图10 不同背网面索力水平下的节点位置Fig.10 Node coordinates of back net under different pretension levels

使用ANSYS软件对所提网面设计方法的正确性进行验证。使用不受压杆单元LINK10对索网进行建模，给定索网的弹性模量为40GPa，索网直径为0.8mm，仿真结果如图11所示。各节点的最大位移为0.705×10-13m，这说明索网各节点在给定张力作用下处于平衡位置，因此本文所提索网设计方法是有效的。

图11 平面工字型索网变形云图Fig.11 Deformation of planer I-shaped cable net

当前网面在金属丝网的作用下具有一定的垂度时，各节点坐标如表2所示。

表2 空间工字型索网各节点坐标Table 2 Node coordinates of Spatial I-shaped cable net

给定前网面张力的水平分量为10N，背网面张力水平分量为20N，算法迭代极限误差为1×10-13，用进退法进行迭代求解。同样使用ANSYS软件进行验证，材料参数与上例相同，金属丝网对索网的作用以外力的形式添加到前网面的节点上，仿真结果如图12所示。各节点的最大位移为0.115×10-13m，验证了所提方法的有效性。

图12 空间工字型索网变形云图Fig.12 Deformation of spatial I-shaped cable net

3 结论

几何与预张力设计直接影响空间索网反射面天线的形面精度，进而影响其电性能。本文提出一种适用于工字型索网的几何与预张力集成设计方法，并进行了算例验证。所提设计方具有较高的精度，可实现对背网面张力水平的控制且不受反射面及边界条件对称性的限制，具有一定的应用价值。