谱元法在空间可展开结构振动带隙分析中的应用①

张 震，李团结，王作为，唐雅琼，范叶森

(1.西安工业大学，西安 710021；2.西安电子科技大学，西安 710071；3.中国空间技术研究院西安分院，西安 710000)

0 引言

空间可展开结构是一种典型的轻质、多柔体周期结构，其在展开、调姿以及空间交变热环境下所产生的振动幅度较大、持续时间长，严重影响设备的正常运行[1-2]。由于空间环境的特殊性及空间设备轻质性等要求，使得结构减振成为了空间可展开结构的主要难题。近几十年来，周期结构受到国内外学者的广泛关注[3-4]。他们对一维周期结构和一些简单的二维、三维周期性梁的波传播特性进行了的研究，如板梁结构、调制棒和加强板等[5-6]。他们的研究揭示了两种带隙机制，即 Bragg 散射机制和局域共振(LR)散射机制。其中，周期结构的带隙主要是 Bragg 散射机制引起的。相关研究表明，经过特殊设计的周期结构具有能够抑制弹性波传播的的频率范围，这个频率范围称为带隙。通过调节周期结构的材料参数、几何形状及尺寸等，可以人为调节带隙的位置、宽度以及对弹性波传播的抑制能力[7-8]。因此，可以利用周期结构的带隙机理来设计结构的减振特性。

对于空间可展开结构，其基本构件为轻质、柔性杆梁结构，结构中的振动可看作是不同频率弹性波的叠加[9]。于是可将空间可展开结构中的弹性波分解成拉压波、扭转波和弯曲波等特征波来分别研究。因此，为了保证空间可展开结构具有良好的结构减振特性，有必要对周期性空间可展开结构的振动带隙进行研究和设计。

由 Doyle 提出的基于傅里叶变换的谱元法，是在频域内建模，并能基于波动解建立与频率相关的插值函数，由此得到的频域解能够精确满足运动方程[10]，可提供精确的频域解。同时，谱元法还对复杂边界具有广泛的适应性、收敛速度快等优点，有重要的应用价值[11]。

本文采用谱元法推导可展开结构主体框架的通用刚度矩阵和谱元方程，并以二维复合梁框架结构和ADAM伸展臂为例，论述谱元法在可展开结构振动带隙特性分析中的应用。

1 空间可展开结构

由于空间可展开结构需要长时间在展开态的下工作，并且要求具有一定的承载能力和保形能力，因此可展开结构的主体结构一般都采用桁架或框架结构来构建，其基本结构构件是较为规则的杆单元或梁单元，因此可以采用谱元法对各结构构件进行建模并装配得到整体框架结构的谱元刚度以及谱元方程，进而计算弹性波在框架结构中传播时的振动频率响应，辅助预测和判断结构的动力学响应问题。

1.1 弯曲波谱元动力学方程

假设可展开结构主体结构为框架结构，其基本单元采用 Bernoulli-Euler 梁单元，则其对应弯曲波的振动方程为：

(1)

其中，wy(x,t)是中轴线法向位移，E是杨氏弹性模量，A0是横截面积，ρ是密度，Iz是关于中性轴转动惯量的截面矩。通过谱元法求解可得到 Bernoulli-Euler 梁弯曲波的谱元方程为：

(2)

其中

(3)

以及

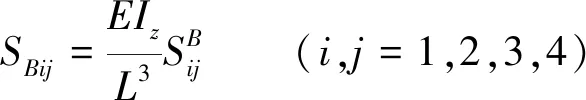
(4)

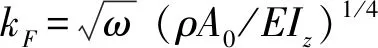
1.2 拉压波和扭转波谱元动力学方程

同理，可以得到 Bernoulli-Euler 梁拉压波和扭转波的谱元方程如下：

(5)

其中

(6)

以及

(7)

1.3 可展开结构主体框架谱元动力学方程

在理想状态下，空间可展开结构的展开态可近似成排列比较规则的周期结构，结合复合梁结构构件在空间位置关系，可以得到空间可展开结构展开态的谱元方程为：

S6N×6N(ω)d6N×1=f6N×1

(8)

其中

N=8mnp-7Rcenter-3Rface-Redge

Rcenter=(m-1)(n-1)(p-1)

Rface=2[(m-1)(n-1)+(m-1)(p-1)+(n-1)(p-1)]

Redge=4[(m-1)+(n-1)+(p-1)](9)

式中，N 表示p层框架的不重复节点总数，m和n分别表示底层单元格的行数和列数，Rcenter表示结构体内部相邻单元间共用的重复节点数，Rface表示结构体外表面相邻单元间共用的重复节点数，Redge表示结构体外部侧棱相邻单元间共用的重复节点数。

2 数值算例

2.1 二维复合梁框架结构

图1是一种由A和B两种材料组成而成的复合结构构件，图2是由该复合构件构建的二维复合梁框架结构。材料A和材料B的具体参数如表1所示，P点是外部激励，Q是检测点。其中，F=F0eiωt，F0=1N。

图1 复合梁结构示意图Fig.1 Schematic diagram of composite beam structure

图2 二维复合梁周期框架结结构Fig.2 Two-dimensional composite beam periodic frame structure

表1 等截面复合梁的几何参数和材料属性Tab.1 Geometric parameters and material properties of composite beams with uniform cross-section

图3是图2所示框架结构的结构单元在0-800 Hz范围内的频率响应与Ansys仿真结果的对比。从图3不难看出，谱元法结果与Ansys仿真结果的前4阶固有频率几乎完全重合，第5-7阶固有频率出现较小误差，第8-9 阶误差较大。例如：第4-7阶固有频率的偏移率分别是1.52%、0.43%和0.90%，第8-9阶固有频率的偏移率分别是2.63%和3.27%。显然，采用谱元法得到的前9阶固有频率与采用有限元法的结果误差在5%以内，是可以用来求解结构的频率响应以及振动带隙问题的。事实上，上述误差主要是有限元法引起的，因为采用该方法做响应分析时高频误差较大。

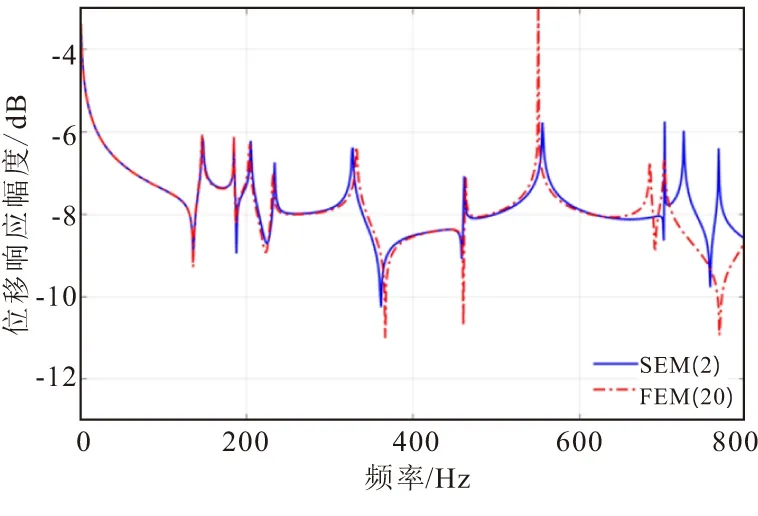
图3 框架结构单元频率响应与 Ansys 仿真结果对比Fig.3 The comparison of frequency response of the structural unit with the results of Ansys simulation

为了更加直观地反映波的传播特性，这里引入振动传递系数。假设符号wi和wo分别表示激励位置和检测位置的横向位移，则弯曲波的传递系数TN可以通过TN=lg|wo/wi|来计算。图4和图5分别是图2所示结构单元和整体框架结构在0-4500 Hz范围内的振动频率响应。

(a)

从图4可以看出，当检测到的位移响应幅度在-8 dB以下且其对应的传输系数在0 dB以下时，其对应的频率范围对波的传播的抑制能力较强，极有可能在这些区域产生带隙。

从图5可以看出，结构的带隙范围可以通过图4进行预测。图5中1065-1360 Hz、1540-1740 Hz、1870-2320 Hz和3010-3780 Hz区域产生了较为明显的带隙，结合图4的相关分析不难发现，图5中带隙的频率范围正好对应图4中对波的传播的抑制能力较强的区域。

从图5还可以看出，带隙的基本形状可以从图4进行预测。例如：图4(b)中1040 Hz、3114 Hz以及3248 Hz对应的传播系数较大但宽度较窄，其位置正好处于抑制能力较强的区域，则在整体结构中可能形成较窄的透射尖峰或者幅值较小的带隙。如图4与图5中实线椭圆形标记区域。再如1740-1870 Hz区域，其传播系数较大、宽度较宽，但其整体传输系数在0 dB以上附近，此部分正好对应图5中对应范围的通带，且能看出明显的两处透射尖峰，如图与图5中虚线椭圆形标记区域。

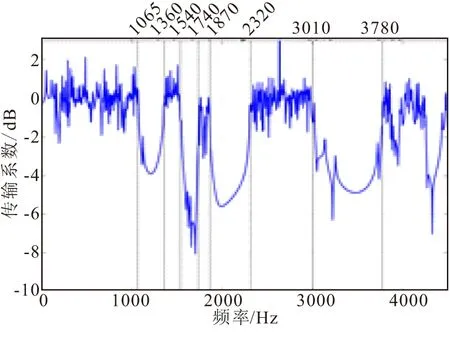
图5 复合梁框架结构频率响应Fig.5 Frequency response of composite beam frame structure

2.2 空间伸展臂

图6是可展开构架式伸展臂(ADAM)[12]，其中，图6(a)和(b)分别是ADAM伸展臂的折展原理和结构单元构成示意图。伸展臂结构单元的长、宽和高分别用L、W和H表示，伸展臂结构的材料用A和B表示。

(a) (b)图6 ADAM 伸展臂及其结构单元Fig.6 ADAM structures and its structural unit

若伸展臂的结构单元的长宽高都是 1 m，且暂时忽略索单元对伸展臂带隙的影响，可以得到图6所示伸展臂主体框架结构的振动频率响应如图7所示。

图7 ADAM 伸展臂(1×10)振动频率响应Fig.7 Frequency response of ADAM structures (1×10)

综上所述，采用谱元法可以求解可展开结构主体框架的动力学响应问题，且频域解具有较高的准确性；可以通过周期框架结构单元的频率响应来预测整体结构的带隙位置和范围，同时也可以预测带隙中的部分透射尖峰。

3 结束语

通过谱元法推导了空间可展开结构主体框架的通用刚度和谱元方程。以二维复合梁框架结构为例，讨论了谱元法在结构动力学响应中仅需要较少单元个数就可获得较高的精确度，并采用有 Ansys 对其结果进行了验证。分析了位移响应幅度和传输系数的相关特性和联系，提出了一种预测结构带隙位置和宽度的方法，并用一般框架结构的频率响应进行了验证。此外，还以ADAM空间伸展臂的振动频率响应为例，说明了谱元法在结构的动力学特性方面具有较为广阔的应用空间。