钒、氮单掺及钒和氮共掺ZnO 可见光光催化性能的模拟计算

左春英，陈佰树，钟成

（1．黑龙江八一农垦大学理学院，大庆 163319；2.中国工程物理研究院核物理与化学研究所）

纤锌矿氧化锌是一种在室温[1-3]下具有较大激子结合能（60 MeV）的宽禁带（Eg=3.37 eV）半导体材料，在电子、光子材料等领域有着广泛的应用，此外，在信息技术、生物技术、纳米科学与工程领域中均具有广阔的应用前景[4-6]。近年来，以ZnO[7]为载体的光催化剂因在环境净化和污水去除领域具有广阔的应用前景而备受关注[8-9]。然而，ZnO 颗粒由于其禁带宽而只能由太阳光谱的UV 部分激活。因此，ZnO 作为光催化剂在太阳光照射下的使用受到限制，这是由于太阳光中紫外光照射（＜387 nm）的比例很低（＜5%）。使用紫外灯不仅价格昂贵，而且对人体有害，因此，从环境和健康的角度出发，采取措施促使ZnO 的光活化区域向可见光方向移动是极其必要的。这可以通过多种方法来实现，其中有效的方法之一就是通过ZnO 掺杂来实现[10]。

实验表明，当ZnO 被Cr、Cd、Cu[11-13]等金属和N、S、C[14-18]等非金属掺杂时，其在可见光区的光催化活性增强。然而，金属掺杂易形成金属团簇，非金属掺杂的溶解度低且电离能高。因此，在ZnO 光催化领域寻找更有效的掺杂方法是有非常意义的一项工作。

TiO2作为一种常见的光催化剂，在实验和理论上都得到了深入的研究。近年来，共掺杂TiO2光催化活性显著提高[19]。ZnO 与TiO2的禁带宽度、导带和价带边缘位置等性质相似，但其电子迁移率比TiO2高10～100 倍，具有较低的电阻和较高的电子传输速率，是一种性能优异的光电器件。近年来，基于密度泛函理论的第一性原理计算方法已广泛应用于材料的晶体结构、电子结构和光学性质等方面的研究，其计算的结果与实验结果符合的很好[20-21]。因此，利用基于密度泛函理论的第一性原理计算方法对未掺杂、V掺杂、N 掺杂、共掺杂ZnO 的电子结构和光学性质进行了计算和比较，其中重点研究了不同浓度的共掺杂ZnO 的光催化性能。

1 计算方法

1.1 理论模型

Ⅱ-Ⅵ族ZnO 是直接宽带隙半导体材料，其稳定相为六方纤锌矿结构。ZnO 属于P63 mc 空间群，晶格参数a=b=3.25 Å，c=5.20 Å，c/a=1.60。

为了研究不同掺杂浓度对ZnO 化合物光活化性质的影响，以1×2×2（含16 个原子，包括8 个氧原子和8 个锌原子）、2×2×2（含32 个原子，包括16 个氧原子和16 个锌原子）、3×2×2（含48 个原子，包括24个氧原子和24 个锌原子）的超胞为基础，构建了6种模型进行了研究。这6 种模型分别是ZnO（Zn16O16）（模型Ⅰ）、Zn15VO16（模型Ⅱ）、Zn16O15N（模型Ⅲ）、Zn23VO23N（模型Ⅳ）、Zn15VO15N（模型Ⅴ）和Zn7VO7N（模型Ⅵ）。如图1 所示为Zn15VO15N 的超胞晶格结构。

图1 2×2×2 V+N 共掺杂ZnO 超胞结构图Fig.1 2×2×2 supercell structure of V+N- codoped ZnO

1.1 计算方法

利用基于密度泛函理论（DFT）和赝势平面波的CASTEP 软件包[22]进行计算，在广义梯度近似（GGA）的框架内处理交换和相互作用[23]。计算中k 点组的布里渊区采样网格参数对于纯ZnO 为9×9×6，对于掺杂ZnO 为4×4×3，平面波能量截断设置为400 eV。

为了确定杂质对结构稳定性的影响，首先对ZnO、Zn15VO16、Zn16O15N、Zn23VO23N、Zn15VO15N 和Zn7VO7N 的超晶格结构进行了优化，得到其晶格参数后对内部坐标进行优化，最后得到精确的结果。在几何优化完成后，我们计算了掺杂系统能带结构、电子态密度和光学性质。

2 结果和讨论

2.1 晶体结构和稳定性分析

计算得到的ZnO 晶格参数a=3.29 Å，c/a=1.61，与a=3.25 Å，c/a=1.60[24]的测量值相符，这保证了模拟结果的可靠性。

材料沿着c 轴的内应力定义为[25]

δ=4.536×1011（c0-c）/c0

公式c0为5.026 Å。计算结果表明，优化后的氧化锌，其c 轴内应力小于零，与实验结果一致，这说明其以拉伸应力为特征。所研究的掺杂系统的内应力均为负值。

从表1 中可以清楚地看出，与纯ZnO 相比，Zn16O15N 体系的总能量由于受体能级之间的相互排斥而增加。但是，由于V、O、N 原子间的吸引相互作用，V 掺杂ZnO 体系的总能量明显降低。此外，V+N共掺杂体系的总能量随V+N 掺杂浓度的增加而进一步降低。

计算了V、N、V+N 掺杂ZnO 的形成能。形成能Ef[26]可以表示为：

Ef=EZno∶V(N，V+N)-EZnO-μV（μN，μV+N）+μZn（μO，μZn+O）

其中EZno∶V(N，V+N)是掺杂了V、N 或V+N 的体系的总能量，EZnO是完美超胞的总能量，μV、μN、μZn、μO是钒、氮、锌或氧分子的化学势，μV+N、μZn+O是钒和氮及锌和氧分子的化学势之和。

对于掺杂材料，可以直接从表1 中发现，N 掺杂的ZnO 体系形成能量为正值，这表明Zn16O15N 不稳定。然而，V 掺杂ZnO 系统的形成能是负值。很明显，共掺杂的形成能小于V 单独掺杂的形成能。

2.2 掺杂浓度的分析

经过几何优化，我们发现Zn15VO16、Zn16O15N、Zn23VO23N、Zn15VO15N 和Zn7VO7N 掺杂体系的杂质浓度分别为2.517×1021cm-3、2.516×1021cm-3、1.689×1021cm-3、2.536×1021cm-3及5.080×1021cm-3，这表明它们是重掺杂退化半导体。

2.3 电子结构的研究

ZnO 晶体的电子结构随着掺入杂质的不同而发生变化，从而使态密度分布也不同。电子结构的变化可以通过能带结构和电子态密度来研究。

2.3.1 能带结构

计算出的纯ZnO 及不同掺杂ZnO 模型的能带结构分别如图2 所示。在图2（a）中观察到，在高度对称点G（Γ）处，直接带隙约为0.73 eV，这与使用DFT的其他计算值如Schleife[27]的0.73 eV 和Janotti[28]的0.80 eV 是一致的，并且由于GGA 的限制，使得计算值要小于3.37 eV 的实验数据。尽管DFT 存在这一缺点，然而这并不影响比较晶体的相关性质的准确性。

对于所有的掺杂ZnO 体系，掺杂后简并度降低，价带和导电带变得致密，但是它们仍属于直接能隙半导体。根据图2（b）、（c）、（d）、（e）和（f）计算了Zn15VO16、Zn16O15N、Zn23VO23N、Zn15VO15N 和Zn7VO7N 的带隙分别为0.75、0.58、0.84、0.87 和0.99 eV。对于N掺杂的ZnO，在价带之上引入未占据的受主能态，从而降低带隙。从图2（c）中可以清楚地看到，由于在价带顶部附近存在多余的空穴，所以通过N 掺入可以实现p 型ZnO。

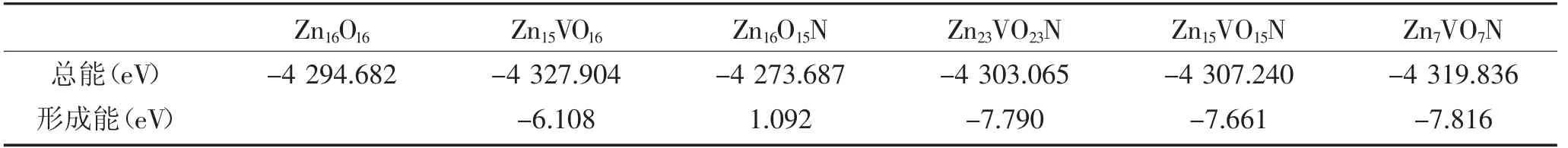
表1 不同结构系统的总能量和形成能Table 1 The total energy in unit cell and formation energy for different structures

图2 掺杂ZnO 系统的能带结构Fig.2 Band structures of pure and doped ZnO

与纯ZnO 相比，V 掺杂氧化锌体系的费米能级上升到导电带形成n 型退化半导体。V 掺入使费米能级与导带底部的差为1.85 eV，随着浓度的增加，其差值分别为1.42、1.47 和1.40 eV，这了表明V 掺杂体系具有金属特性。通过比较这些值，我们发现Zn15VO15N 是共掺杂体系中金属性质最强的。经过计算，Zn15VO16、Zn16O15N、Zn23VO23N、Zn15VO15N 和Zn7VO7N体 系 的 光 学 带 隙 分 别 为2.60、0.20、2.25、2.35 和2.39 eV。掺杂体系的光学带隙变窄其原因在于：一方面，高浓度载流子使光吸收边向低能方向移动，使光带隙变宽导致掺杂体系出现Burstein-Moss 移动[29]。另一方面，电荷之间的相互作用导致多体效应，致使光带隙变窄[30]。但多体效应对带隙的影响比Burstein-Moss 效应大，因此V、N 单掺及V+N 共掺杂均使光能隙变窄。

2.3.2 态密度

为了更好地分析电子性质，我们计算了态密度。对于纯ZnO，图3 描绘了价带中的两个区域，-5.73到-3.98 eV 能区主要由Zn-3d 和O-2p 组成，-3.98到0 eV 能区主要由O-2p 态组成。ZnO 的导带主要来自Zn-4s 和Zn-3p 态，与Zn-4s 和Zn-3p 的导带价电子相比，上价态O-2p 的轻微变化说明空穴有效质量较大，迁移率较小。

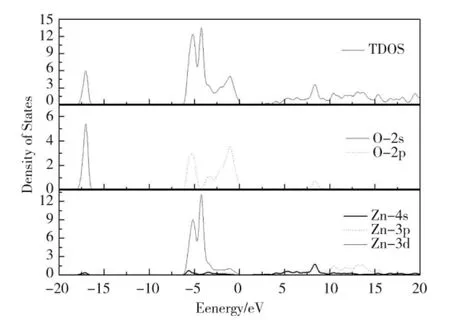
图3 纯ZnO 的态密度Fig.3 The density of states of pure ZnO

当V 作为取代原子掺杂时，费米能级附近的导带主要来源于V 位的3d 态和Zn 位的4s 态。对于所有V 掺杂的体系，处于-0.58～2 eV 能量范围的V-3d 态劈裂成两部分。对于Zn7VO7N 体系，V-3d 态变宽（-0.77～2.52 eV）且3d 峰的劈裂强度变弱；在-40.02 和-66.12 eV 中存在两个窄价带区，它们分别来自V-3p 和4s 态。与未掺杂的ZnO 相比，掺杂V 体系，O原子能态移入2.40 eV 的低能区；掺杂N 体系，O 原子能态保持不变；掺杂体系，对于Zn23VO23N，Zn15VO15N 和Zn7VO7N 系统，O 原子能态分别移入到1.86、2.03 和2.32 eV 的低能区。与未掺杂ZnO 相比，对于V 掺杂系统的Zn 的总态密度均会移动到大约2.40 eV 的低能区，然而，对于N 掺杂体系的Zn 的总态密度保持不变。与N 掺杂ZnO 相比，V+N 掺杂导致N-2s 态移动到2.01 eV 的高能区和N-2p 态移到2.83 eV 低能区。通过分析发现，V-3d 态对掺杂ZnO结构的性质有重要影响。

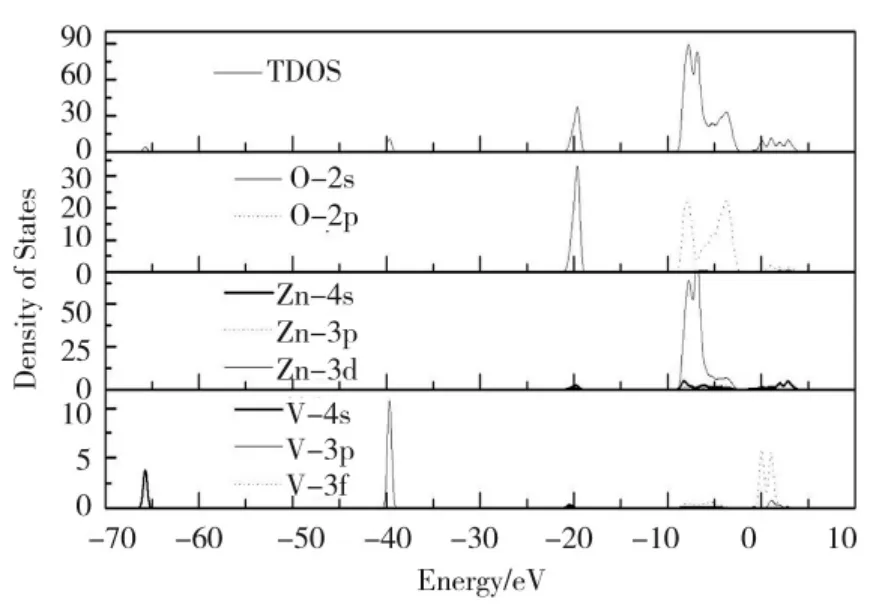
图4 V 掺杂体系的ZnO 态密度Fig.4 The density of states of V-doped ZnO

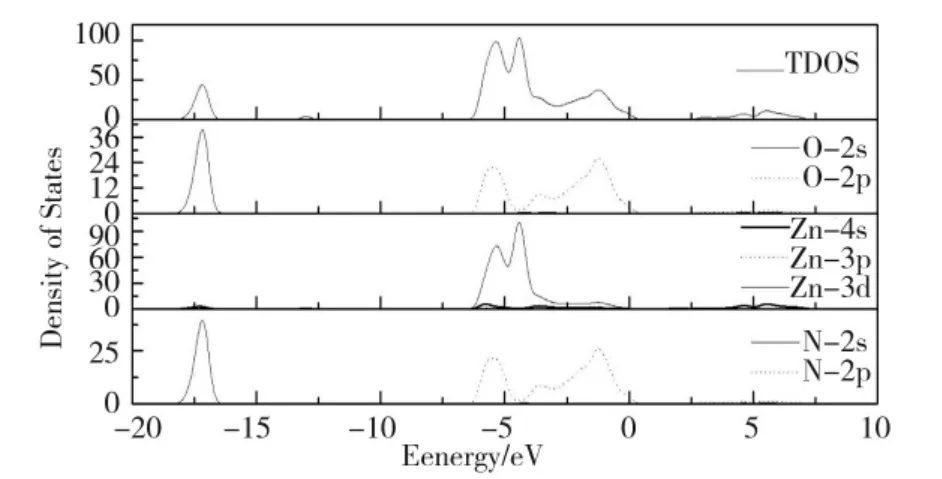
图5 N 掺杂ZnO 体系的态密度Fig.5 The density of states of N-doped ZnO

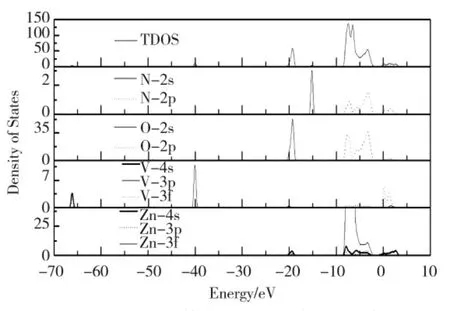
图6 V+N 共掺杂ZnO 体系的态密度Fig.6 The density of states of V+N- codoped ZnO

2.4 光学性质

最后，计算了纯ZnO 和另外五种掺杂模型的光学常数，包括介电常数和吸收光谱，分别如图7 和8所示，它们被剪子算符（剪子算符=3.37 eV-7.3 eV=2.64 eV）校正。

图7 未掺杂和已掺杂ZnO 体系的介电函数Fig.7 Dielectric function of undoped and doped ZnO

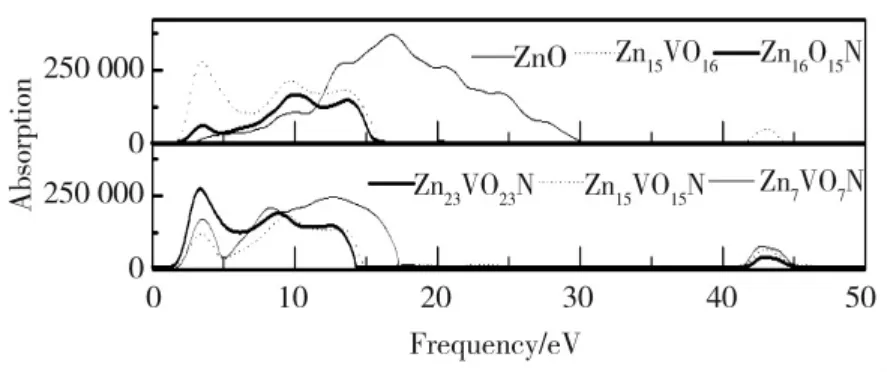
图8 未掺杂及已掺杂ZnO 体系的光吸收谱Fig.8 Optical absorption spectra of undoped and doped ZnO

众所周知，系统中光子与电子的相互作用可以用基态电子的含时微扰论来描述。占据态和未占据状态之间的光学跃迁是由光子的电场引起的。由激发态形成的光谱可以由价带和导带之间的态密度来描述。介电函数的虚部对于任何材料的光学性质都是非常重要的，它可以由占据态和未占据态之间的动量矩阵元来计算。介电函数的实部可根据著名的Kramer-Kronig 关系从虚部计算得出。所有其他光学常数，均可以从介电函数的实部和虚部推导得出。

对于从Ⅰ到Ⅵ6 个掺杂模型，计算的静态介电常数ε1（0）分别是3.66、16.05、4.96、14.45、5.02 和9.16 eV。纯ZnO 的介电函数实部在3.14 eV 达到峰值，主要由价带顶部到导电带底部的电子跃迁产生。然而，对于掺杂的ZnO（模型Ⅳ、Ⅴ和Ⅴ），其峰值在2.08、2.18 和2.25 eV 处，主要是由价带顶到费米面的电子跃迁产生的。根据ε1（ω）值，我们发现，当光子能量分别大于15.24、2.78、3.01 和3.11 eV 时，纯ZnO和共掺杂ZnO 将变成类金属。

从图7 中可以清楚地看出，ZnO 的介电函数ε2（ω）的吸收部呈现出三种结构，分别位于4.18、9.15、12.86 eV 处，这与实验结果[31]一致。位于4.18 eV 处的峰主要来自O-2p 和Zn-4s 轨道之间的电子跃迁。位于约9.15 eV 附近的峰来自于Zn-3d 和O-2p 轨道之间的电子跃迁。在约12.86 eV 附近的较弱的峰主要来自于Zn-3d 和O-2s 轨道之间的光学跃迁。对于掺杂体系，从图7 可以观察到ε2（ω）的第一个峰分别位于2.83、0.53、2.75、2.87 和2.95 eV 处，表明这些吸收边发生红移，ZnO 的光催化活性增强。值得注意的是，在我们的计算中，通过比较峰的宽度和高度[32]，N 掺杂ZnO 系统在可见光区没有表现出良好的吸收活性。根据能带图和态密度图，V 掺杂ZnO 的第一个峰位于2.83 eV 处，主要来自V-3d 态和Zn-4s 态之间的电子跃迁。对于掺杂ZnO 体系，其第一个峰位于约2.80 eV，主要由V-3d、N-2p 和Zn-4s 轨道之间的光跃迁产生。

图8 表明纯氧化锌的吸收光谱范围主要在紫外区，而在可见光区几乎没有吸收光谱。可见，在ZnO晶格中掺入V 可使可见光区的光吸收增加，从而提高了ZnO 的光催化活性。其中，Zn23VO23N 被认为是最好的光催化剂。此外，对于纯ZnO，光学响应范围更宽，约为30 eV，而掺杂氧化锌的响应宽度变窄，约为18 eV。然而，对于V 掺杂的ZnO 体系，在43 eV附近有一个较窄的吸收峰，光子诱导的电子跃迁主要来源于Zn15VO16的V-3p 态和Zn-4s 态之间的跃迁，以及Zn23VO23N、Zn15VO15N 和Zn7VO7N 的V-3p、N-2p 和Zn-4s 之间的跃迁。

3 结论

综上所述，利用基于密度泛函理论的平面波超软赝势技术的第一性原理计算，研究了V、N、V+N-掺杂ZnO 的形成能、能带结构、总态密度、分波态密度和光学性质。我们的主要结论可以概括如下：

（1）通过比较掺杂ZnO 体系的形成能，我们发现共掺杂ZnO 体系更加稳定。

（2）能带结构计算表明，所研究的化合物体系均属于直接带隙半导体，此外，掺杂ZnO 系统的光学带隙比纯ZnO 的光学带隙窄。

（3）对于掺杂ZnO 体系，费米能级附近的导带主要来源于V-3d 态和Zn-4s 态。通过计算分析，V-3d 态对掺杂ZnO 结构的性质有重要影响。

（4）光学性质的计算结果表明，与纯ZnO 相比，V、N 及V+N 掺杂ZnO 体系的吸收边红移非常明显。对于Zn23VO23N 掺杂体系，在363 nm 处有一个强吸收峰，其吸收宽度在26～939 nm 之间，这说明了该化合物是一种比较好的光催化剂。