五年级数学期末综合评价

○郭辉杰

一、填空

1.计算3.7×0.9，先按照整数乘法的法则计算（ ）×（ ），得（ ），再看因数中一共有两位小数，就从积的右边起数出（ ）位，点上小数点，最后得数是（ ）。计算25.5÷0.11，先利用（ ）的规律，把除数和被除数同时扩大（ ）倍，计算（ ）÷（ ），然后计算得数，用循环小数的简便记法表示为（ ），保留两位小数约等于（ ）。

2.根据12×4=48，写出下面各算式的得数。

1.2×4=（ ），0.12×0.4=（ ），0.48÷0.12=（ ）。

3.小华在教室的位置是第5列第3行，可以用数对表示为（ ，）；小凯在教室的位置用数对表示为（2，4），则小凯是第（ ）列第（ ）行；小云与小华在同一列，与小凯在同一行，可以用数对表示为（ ，）。

4.写一个方程（ ），使它的解是x=7。

5.两个因数的积是6.08，其中一个因数扩大10倍，另一个因数缩小100倍，这时积是（ ）。

6.一个平行四边形的面积是90平方厘米，底是15厘米，则它的高是（ ）厘米。如果一个三角形和它等底等高，则三角形的面积是（ ）平方厘米。

7.疫情发生后，某小学储备了一批防疫物资。其中口罩每只3.2元，共购买了a只；洗手液每瓶22.5元，共购买了b瓶。用含字母的式子表示购买口罩的钱数为（ ），购买洗手液的钱数为（ ），当a=2000，b=80时，学校购买这两项物资共花费（ ）元。

8.一辆汽车行驶100千米需要8升汽油，平均每升汽油可以行驶（ ）千米，每千米需要汽油（ ）升。

9.用载重为4.2吨的汽车运送一批20吨的货物，最少需要（ ）辆可以一次运完；做一套成人服装用布2.6米，200米布可以做成人服装（ ）套。

10.在〇里填上“<”“>”或“=”。

4.8×1.2〇4.8 5.6÷1.2〇5.6

0.8×12.5〇12.5÷0.7 0.82〇0.8

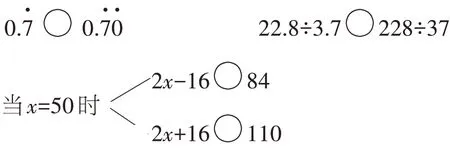
11.三个连续自然数的和为135，则这三个自然数中最大的一个是（ ）。

12.一个梯形的高是9厘米，如果上底减少5厘米，它就变成一个三角形；如果上底增加4厘米，它就变成一个正方形。这个梯形的面积是（ ）平方厘米。

13.一个盒子有红、黄两种颜色的球共10个，其中红球有2个，从中任意摸出一个球，则摸到黄球的可能性比摸到红球的可能性（ ），（ ）摸到绿球（提示：填“可能”或“不可能”）。

14.鸡兔同笼，从上面看有25个头，从下面数有80条腿，则鸡有（ ）只，兔有（ ）只。

15.在长为500米的景观路两侧栽梧桐树（景观路的两端也要栽），每两棵梧桐树的间距是10米，一共需要栽梧桐树（ ）棵。如果每两棵梧桐树之间再栽一棵海棠，则需要栽海棠（ ）棵。

二、选择

1.计算1.23×0.84，得数是（ ）。

A.1.0332 B.0.7652

C.1.202 D.1.1344

2.两个数的商是6.18，如果被除数扩大10倍，除数扩大100倍，则商是（ ）。

A.6.18 B.0.618

C.61.8 D.618

3.一个小数用四舍五入法保留一位小数后约等于3.6，则这个小数不可以是（ ）。

A.3.64 B.3.605

C.3.55 D.3.545

4)模型预测结果与实验得到的侵彻深度、侵彻模式、残余质量和时程曲线等数据吻合得较好，验证了本文理论模型的准确性。

4.下列式子中，（ ）是方程。

A.9+8=17 B.x+5>6

C.3x=24 D.12+x-7

5.先将点（1，1）、（5，1）连线，下列各点中与原来两点连线后不能构成三角形的是（ ）。

A.（1，2） B.（3，1）

C.（4，3） D.（5，3）

6.故宫的九龙壁是中国传统建筑中用于遮挡视线的墙壁，九龙壁正面长29.47米，高3.59米，估计它的面积不会超过（ ）平方米。

A.60 B.80

C.90 D.120

A.周长和面积都变大

B.周长没有变，面积变小

C.周长和面积都没有变

D.周长和面积都变小

8.A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行，经过3小时相遇。已知甲车每小时行驶80千米，求乙车的速度。下列式子错误的是（ ）。

A.（450-80×3）÷3 B.450÷3-80

C.（450-80）÷3

D.设乙车每小时行驶x千米，则可以列方程3x+80×3=450

9.为算式4×1.8选择一个合适的情境，不可以···是（ ）。

A.一个正方形的边长是1.8米，求正方形的周长

B.每支笔的价格是1.8元，求买4支笔所用的钱数

C.一头大象重4吨，是一头犀牛体重的1.8倍，求犀牛的体重

D.一个人步行的速度是4千米/时，求他1.8小时所行的路程

三、判断

（ ）1．两个数相乘，一个因数扩大10倍，另一个因数缩小10倍，积不变。

（ ）2.三角形面积等于平行四边形面积的一半。

（ ）3.一个数乘大于1的数，积大于原来的数。

（ ）4.因为22=2×2，所以32=3×2。

（ ）5.等式两边乘同一个数，或除以同一个数，等式两边仍然相等。

（ ）6.两个完全相同的三角形一定可以拼成平行四边形。

（ ）7.近似数6.8与6.80是相等的，所以这两个数没有区别。

（ ）8.数对（5，6）与数对（6，5）表示的位置不同。

四、计算

1.直接写得数。

3.2×4= 12÷5= 8.1÷0.9=0.2×0.45= 16.16÷4= 3÷0.3=5.7+5.3= 1.6÷100= 0.32=

0×3.68= 0.035×100= 18.9÷9=

4×（1.5+0.25）= 0.25×4÷0.25×4=

2.列竖式计算。

0.56×0.05 12.6÷0.28

3.脱式计算。（能简算的要简算）

5.7+3.25+7.75+6.3 23.5-6.7-3.3

0.25×32×0.125 99×3.65+3.65

0.92×102 17.5-7.5×2

0.37×64+37×0.37 0.666×7+0.222×79

4．解方程。

4x+8.2=36.2x+4.6=4.6

x÷2.9=5 13x+15x=5.6

4（3x-5）=10 5x-3×2.8=14.6

五、解决问题

1.某品种小麦平均株高1.1米，某品种玉米平均株高比这种小麦株高的2倍还多0.05米，求这种玉米的平均株高是多少米？

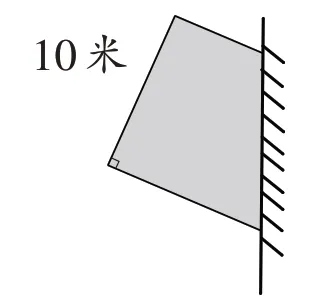
2.李爷爷用48米长的篱笆在靠墙的地方围了一块直角梯形菜地（如图），求梯形菜地的面积。

3.某城市出租车的起步价（路程在3千米以内）是10元，超过3千米的部分，每千米1.5元，张老师从家坐出租车到人民广场付了19元。张老师家到人民广场的路程大约是多少千米？

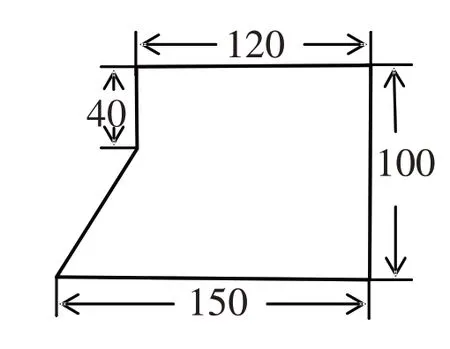
4.幸福村有一块如图所示的小麦田，请你求出小麦田的面积，合多少公顷？（单位：米）一台联合收割机每小时可以收割0.5公顷小麦，这块地需要几小时才能收割完？

5.某防护服加工厂接到一批防护服生产任务，原计划每天生产1.8万套，需要4天完成任务。实际生产中，该工厂改进了技术，提高了生产能力，每天多加工0.6万套。求该厂实际用几天完成加工任务。

6.某地为鼓励居民节约用电，电费结算采用分档计价方式。当月用电量不超过180千瓦时，每千瓦时0.52元；当月用电量超过180千瓦时，超过的部分每千瓦时加收0.05元。

（1）若小宇家某月用电200千瓦时，则当月应缴电费多少元？

（2）若小青家当月用电平均每千瓦时电费是0.53元，求小青家当月用电量。（用方程解）

7.悦悦和彤彤沿着一个圆形广场周围散步，她们发现在广场周围均匀分布着6杆路灯。已知两杆路灯的间距是50米，悦悦每分钟步行80米，彤彤每分钟步行70米，悦悦和彤彤从同一地点出发。

（1）求圆形广场的周长。

（2）若悦悦和彤彤同时出发，背向而行，多长时间可以首次相遇？