坡道长度对货车制动热负荷的影响
张宗威
坡道长度对货车制动热负荷的影响
张宗威
(西南交通大学机械工程学院,四川 成都 610031)
川藏铁路特殊的地形、地势造成沿线坡道长度顺势延展,坡道长度增加将导致货运列车匀速下坡制动工况更加恶劣。采用ANSYS有限元软件建立货车新轮三维有限元模型,针对坡道长度10~20 km连续延展的不同坡长工况,进行货运列车匀速下坡制动热负荷分析,采用间接耦合法计算车轮热应力场。仿真结果得出新轮在不同坡长条件下温度云图、热应力云图以及最高温度与最大热应力时间历程曲线,体现坡道长度增加对最高温度和最大热应力均有提高作用,但增幅逐渐减小;同时,对比车轮辐板圆角径向热应力可知,辐板疲劳裂纹易发生于轮辋与辐板过渡内圆角。
川藏铁路;踏面制动;温度场;热应力
川藏铁路起于四川成都终至西藏拉萨,沿线由四川盆地低海拔地区跃至青藏高原高海拔地区,地势起伏巨大、地形复杂、昼夜温差大。川藏铁路为客货共线铁路,因此线路设计必须同时满足客货车牵引制动要求,确保列车运行安全性。川藏铁路沿线巨大的海拔高度差势必导致坡段坡度加大至加力牵引坡度(20‰以上),坡长顺势延展。
踏面闸瓦制动为我国货运列车基础制动方式,其依靠闸瓦与踏面的摩擦将列车动能转化为热能,以实现列车减速或停车。国内外众多专家学者针对货车和地铁车辆闸瓦制动进行了大量的研究;A.-L. Cristol-Bulthé等[1]在专门设计的制动摩擦系统上再现了紧急制动工况,通过红外热成像在圆盘轨道上观察到的热现象具有特征性,并与摩擦系数的演变相关。肖绯雄等[2]采用热-结构顺序耦合法对高摩合成闸瓦在不同工况下进行瞬态温度场和热应力场分析,得出制动工况越恶劣闸瓦每万公里的磨耗量越大,最大值为21 mm/(万km)。张萍等[3]建立了车轮ANSYS有限元模型,计算分析移动热源和均布热源两种不同热流密度加载方式下,车轮三维瞬态温度场和热应力场,结果表明采用均布热源法计算车轮踏面制动热负荷简捷、准确。姚伟伟等[4]建立了闸瓦与机车车轮的踏面制动摩擦接触数学模型,利用Marc有限元软件,采用热-机耦合法对制动热过程进行了仿真计算,仿真结果与理论分析相符,验证了所构建模型和所选用计算方法的正确性。
上述文献从试验研究、数值仿真等角度对车辆闸瓦制动下车轮热负荷问题进行分析探究。由于川藏铁路沿线特殊的地理环境,坡道坡长设计将会顺势延长,而坡长的增加导致列车下坡制动距离的增加且车轮承载的热负荷进一步恶化;因此本文以川藏铁路为研究背景,分析不同坡长条件对货运列车匀速下坡制动车轮热负荷的影响。
1 有限元模型及边界条件
1.1 有限元模型
C70型敞车是我国铁路现行货运车辆使用最多的一种敞车,其载重大、自重轻,搭配转K6型或转K5型转向架,车辆最高运营速度达120 km/h,满足提速要求[5]。本文选用C70型敞车作为货运车辆,利用ANSYS有限元软件建立货车新轮三维有限元模型,如图1所示。

图1 新轮三维有限元模型
鉴于轮对结构对称性和轮轴过盈配合的结构应力对制动热应力的影响很小,因此本文只建立了单一新轮有限元模型。新轮直径840 mm,模型包含137880个节点和126240个单元;材料采用CL60,车轮热负荷计算涉及非线性分析,需考虑温度对材料力学参数的影响[6],材料力学参数随温度的变化见表1。

表1 车轮材料力学参数
1.2 边界条件
采用ANSYS在坡道长度10~20 km连续延展的条件下针对货运列车匀速下坡制动进行车轮瞬态热分析。根据传热学理论,求解踏面闸瓦制动下车轮非稳态导热微分方程,描述车轮内部温度场内在规律,需要确定其相应定解条件;包含第二类边界条件:给定车轮踏面与闸瓦接触面任意时刻热流密度,第三类边界条件:给定车轮表面与周围环境间的对流传热系数及周围环境温度[7]。
(1)热流密度
采用均布热源法施加热流载荷[3]。根据能量守恒定律,摩擦热能由列车加速下滑力做功转化而来,即采用空气制动,制动力与列车加速下滑力相平衡,控制列车匀速下坡,列车总制动力为:

式中:为列车总制动力,kN;、分别为机车整备质量和牵引质量,=200 t,=2000 t;为坡度千分数,=24‰;、分别为机车和车辆单位基本阻力[8],N/kN。
实际制动过程中,由于轮轨摩擦、空气阻力等因素的存在,车轮只吸收了一部分车辆制动产生的摩擦热能[9],因此实际车轮踏面热流密度为:
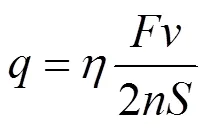
式中:为热流密度,kW;为热流分配系数[10-11];为机车与车辆的总轴数;为下坡匀速,=70 km/h;为闸瓦与踏面摩擦环带面积,m2。
(2)对流传热系数
根据传热学理论,影响对流传热系数的因素与影响流动的因素及流体本身的热物理性质相关[7]。根据众多研究表明,车辆制动过程中,车速是影响车轮表面对流传热系数大小的主要因素,因此表面对流传热系数取为[12]:
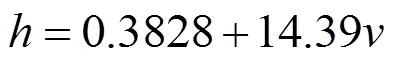
(3)环境温度
初始环境温度为20 ℃。
2 计算结果及分析
2.1 瞬态温度场分析
针对坡道长度10~20 km(坡长值逐级递增2 km)连续延展的不同坡长工况,将边界条件施加至有限元模型后,对不同坡长工况进行瞬态热分析,得出不同坡长条件下货运列车匀速下坡制动新轮热负荷仿真结果。
图2、图3分别为14 km坡长条件下新轮最高温度场云图和不同坡长条件下新轮最高温度时间历程曲线。如图2所示,当坡道长度为14 km时货运列车匀速下坡制动新轮最高温度为324.413 ℃,其最高温度位置位于车轮踏面与闸瓦摩擦环带区,车轮踏面温度场沿周向均匀分布。如图3所示,在制动初始阶段,车轮踏面与闸瓦接触摩擦产生高热且传递至车轮踏面,从而车轮踏面温度迅速升高,车轮最高温度随时间急剧上升;随着货运列车持续匀速下坡制动,摩擦热量不断传递至车轮踏面且传导至轮辋内部,由于温度的不断升高,而车轮材料的比热容顺势升高,因此车轮升高单位温度所需吸收的热量增加,但由1.2节可知,车轮踏面热流密度输入值恒定,从而车轮温升逐渐放缓;在制动结束至冷却阶段,车轮热量输入停止并与周围环境空气发生对流传热,车轮最高温度随时间迅速下降。根据图3可知,不同坡长条件下车轮最高温度随时间变化曲线趋势相同,呈“帆船状”分布;坡长由10 km增长至20 km,车轮最高温度从296 ℃逐级升至348 ℃。
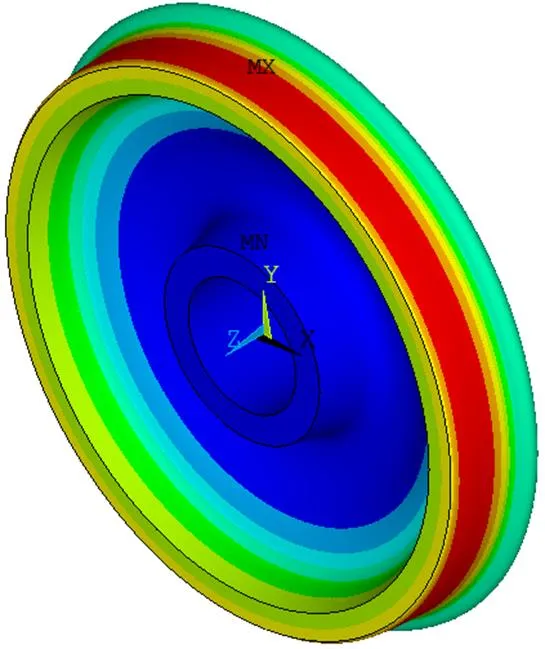
图2 14 km坡长条件下新轮最高温度场云图
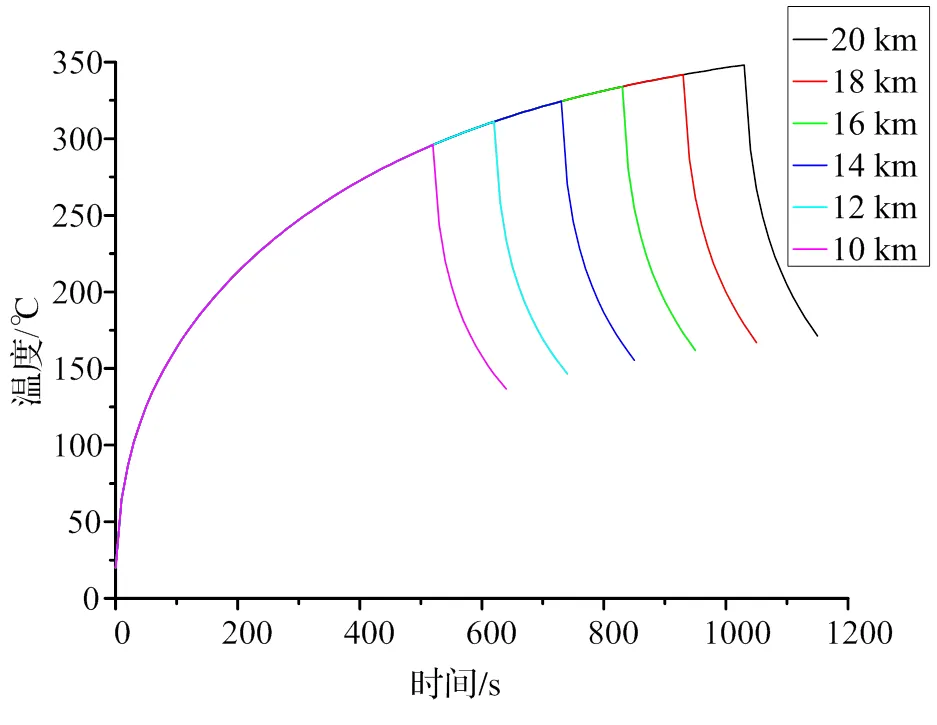
图3 不同坡长条件下新轮最高温度时间历程曲线
图4、图5分别描述了不同坡长条件对车轮踏面节点在车轮横向方向上以及轮辋区节点在车轮径向方向上的温度分布的影响。如图4所示,任意坡长条件下,车轮踏面节点温度从车轮外侧面至轮缘内侧面先升高再缓慢下降最后急剧降低,在距离车轮外侧面横向约0.04 m时到达最高温度;在靠近轮缘侧,由于轮缘增厚导致散热面积增加同时使得导热减缓,因此车轮踏面节点温度在轮缘侧急剧下降;随着坡长的增长,车轮踏面温度整体逐渐升高,但增幅逐渐减小。如图5所示,在最高温度时刻,轮辋区节点温度沿车轮径向呈线性分布;同一坡长条件下,轮辋区节点温度随轮辋区节点距踏面径向距离的增加而逐渐降低。
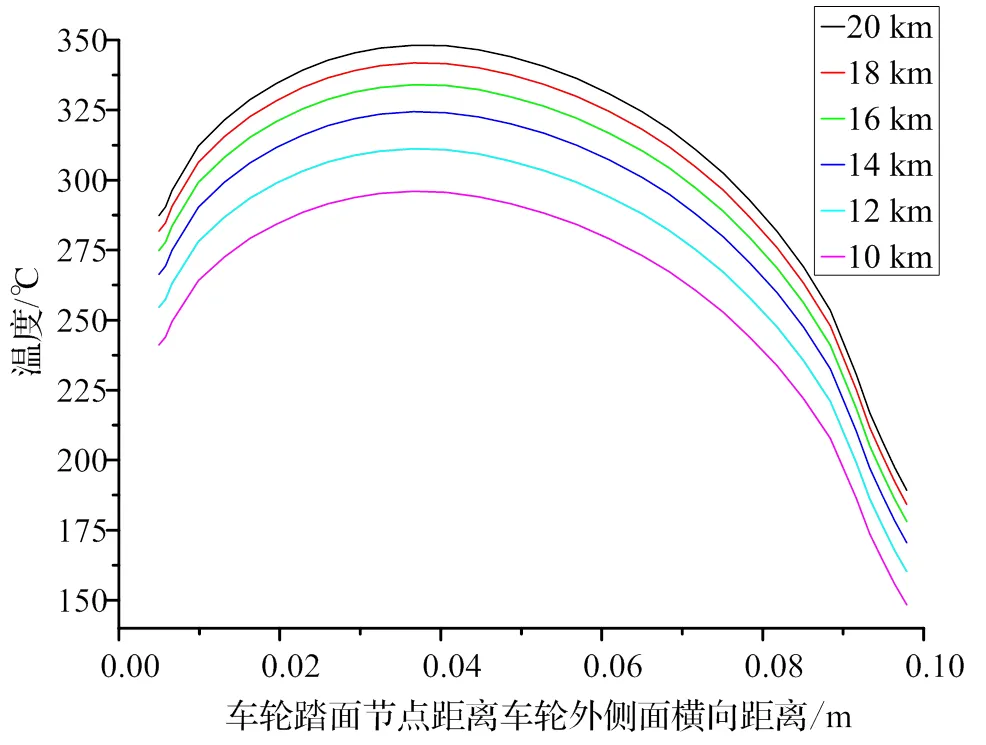
图4 最高温度时刻车轮踏面节点沿车轮横向方向温度值
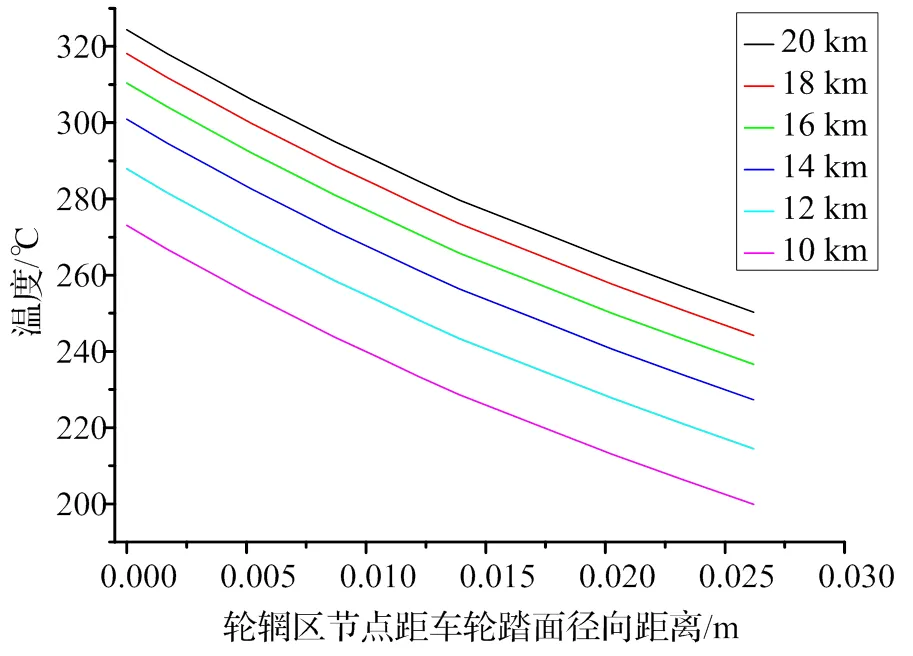
图5 最高温度时刻轮辋区节点沿车轮径向方向温度值
2.2 热应力分析
本文采用间接耦合法计算车轮热应力,在采用SOLID70热单元对车轮进行瞬态热分析后,将SOLID70热单元转换为SOLID185结构单元,并将瞬态热分析中求得的节点温度作为体载荷施加到有限元模型上,同时对轮轴配合面施加位移全约束再进行结构应力分析。
图6、图7分别为14 km坡长条件下新轮等效热应力云图和不同坡长条件下新轮等效热应力时间历程曲线。车轮温度发生变化时,由于内部和外部的约束作用,将对车轮内任一点造成一定的应力,使该点与温度变化对应的热变形,部分或全部地不能产生。如图6所示,在货运列车匀速下坡制动开始时刻,踏面温度骤升,而轮辋、辐板区温度较低,因此最高温度梯度位于踏面,从而车轮最大等效热应力也位于踏面;随着制动持续进行,踏面处热量不断传导至轮辋内部和辐板,从而轮辋区等效热应力逐渐增大,但最大等效热应力依然位于踏面;在制动结束时刻,由于热量不断传导至轮辋和辐板,最高温度梯度转移至轮辋与辐板过渡区,因此最大等效热应力同样转移至辐板区,最大等效热应力为287 MPa;制动结束之后,热量停止输入,但轮毂温度较低,车轮内部残余热量继续向辐板下部、轮毂传导,且最高温度梯度与最大等效热应力转移至辐板与轮毂过渡外侧面。如图7所示,不同坡长条件下车轮最大等效热应力时间历程曲线与最高温度曲线增长趋势相同。
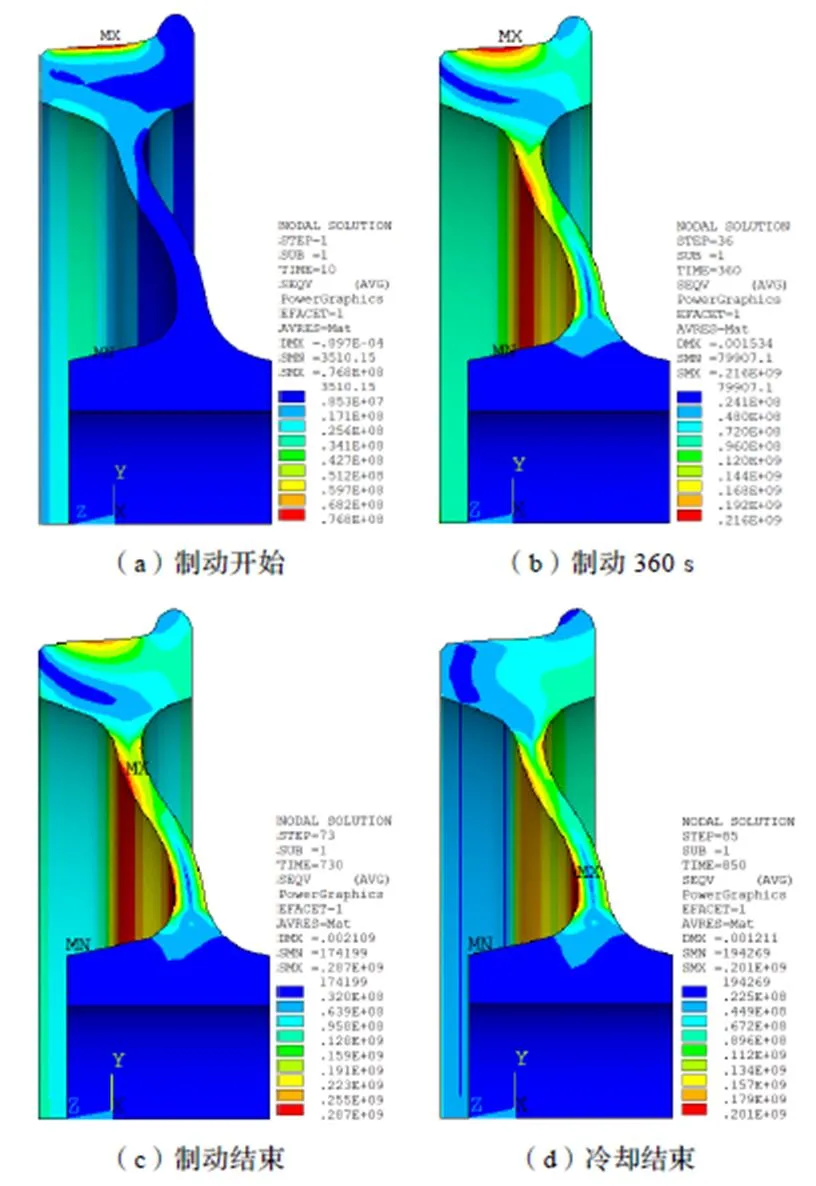
图6 14 km坡长条件下新轮等效热应力云图

图7 不同坡长条件下新轮最大等效热应力时间历程曲线
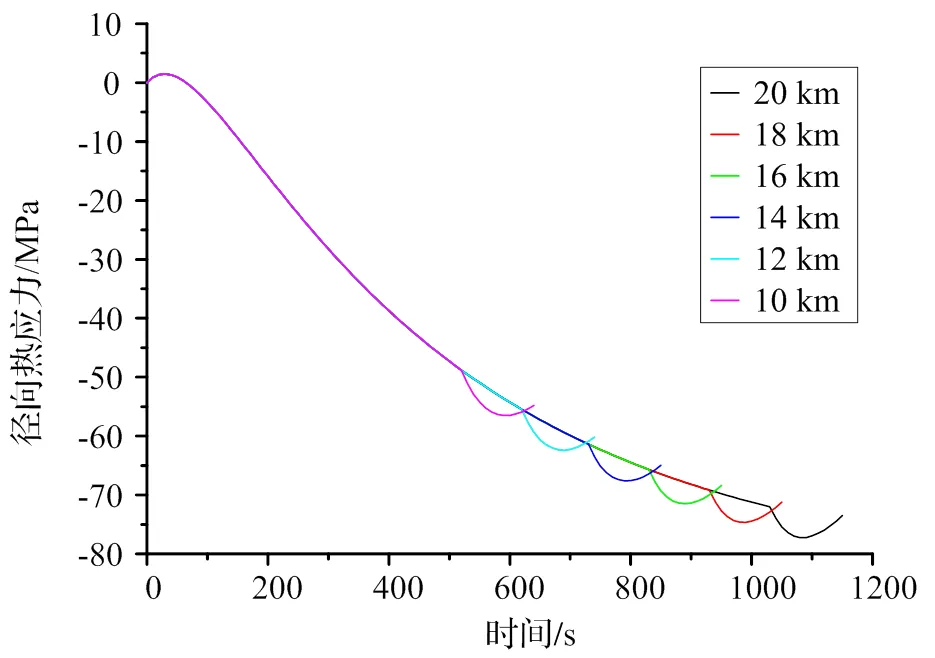
据调查,辐板疲劳裂纹在50 mm以上约占78%,其中400 mm以上占33.3%,最长可达815 mm,裂纹产生的部位多位于轮辋与辐板过渡的圆弧处[13];同时,影响车轮裂纹发展的应力主要为与其垂直的径向应力。因此,本文选取如图8所示车轮辐板圆角位置,分析车轮不同辐板圆角位置的径向热应力。
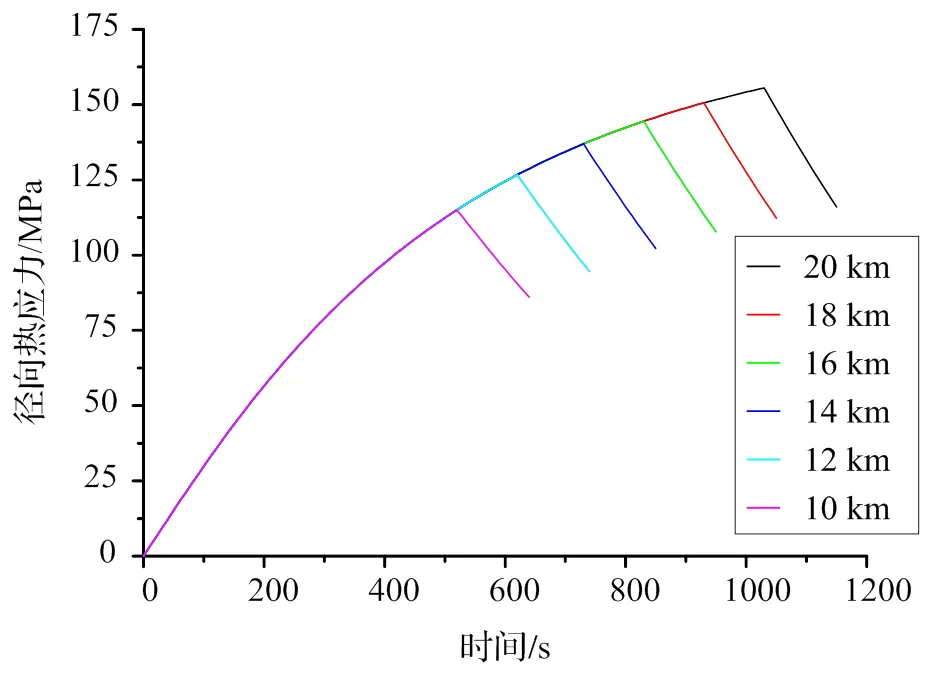
图9为车轮辐板圆角径向热应力时间曲线,由图9可知,辐板圆角位置1在制动初始时刻为径向拉应力后迅速转变为压应力且逐渐增大,在制动结束时因热量输入突然停止、车轮对流散热从而其径向压应力数值产生波动;辐板圆角位置2和位置3均为拉应力,其数值先增大后减小,随着坡长的增长其最大径向拉应力逐级增加;辐板圆角位置4表现为压应力,在制动和冷却过程中,其径向压应力先增大后减小。
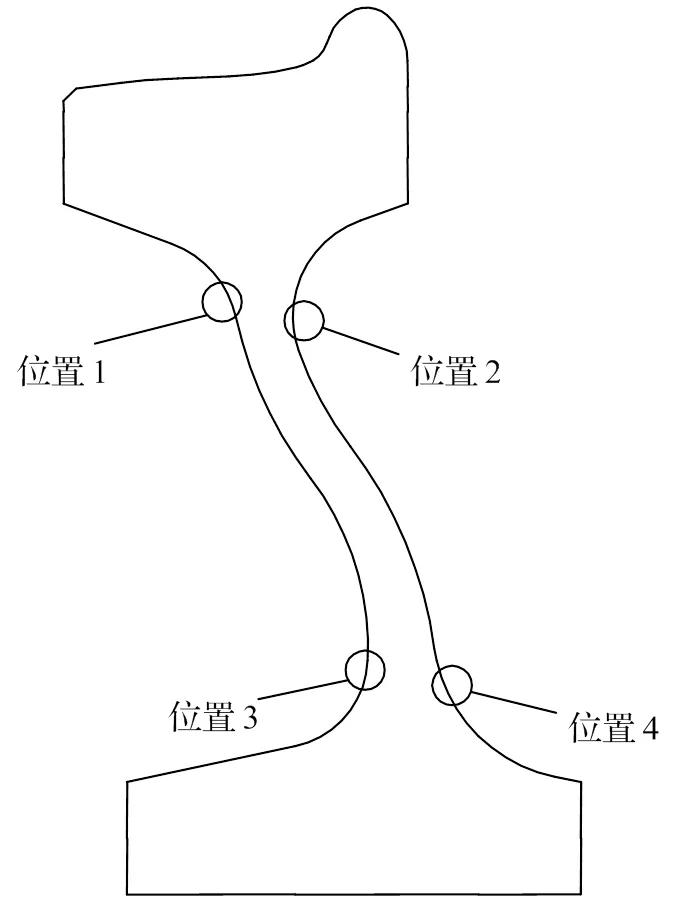
图8 车轮辐板圆角位置编号
3 结论
(1)货运列车匀速下坡制动,车轮最高温度随时间变化呈“帆船状”分布;随着坡长的增长,车轮踏面最高温度逐级递升,但增幅逐级降低;轮辋区节点温度沿车轮径向线性下降。
(2)在热应力仿真过程中,车轮最大等效热应力位置由车轮踏面逐渐转移至轮辋与辐板过渡外侧面和轮毂与辐板过渡外圆角;车轮等效热应力时间历程曲线变化趋势与最高温度曲线趋势基本相同。
(a)位置1
(b)位置2
(c)位置3
(d)位置4
图9 车轮辐板圆角径向热应力时间曲线
(3)车轮辐板圆角径向热应力数值先增大后减小;轮辋与辐板过渡外圆角、轮毂与辐板过渡内圆角受压,轮辋与辐板过渡内圆角、轮毂与辐板过渡外圆角受拉;辐板疲劳裂纹易发生于轮辋与辐板过渡内圆角(从热应力角度,其径向拉应力值最大)。
参考文献:
[1]A.-L. Cristol-Bulthé,Desplanques Y,Gérard Degallaix. Coupling between friction physical mechanisms and transient thermal phenomena involved in pad–disc contact during railway braking[J]. Wear,2007,263(7):1230-1242.
[2]肖绯雄,陈旭. 恶劣工况下货车高摩合成闸瓦磨损分析[J]. 北京交通大学学报,2014,38(4):20-25.
[3]张萍,温泽峰,吴磊,等. 不同热流加载方式下车轮踏面制动温度和应力场模拟分析[J]. 润滑与密封,2013,38(5):69-74.
[4]姚伟伟,何忠. 闸瓦踏面制动热过程的仿真研究[J]. 机械,2009,36(11):1-3,6.
[5]严隽耄. 车辆工程[M]. 3版. 北京:中国铁道出版社,2008.
[6]王京波. 合成闸瓦对车轮热影响的研究[J]. 铁道机车车辆,2003,23(S2):74-79.
[7]杨世铭,陶文铨.传热学[M]. 4版. 北京:高等教育出版社,2006.
[8]张雪才. 和谐系列货运电力机车牵引质量研究[J]. 铁道工程学报,2014(2):96-102.
[9]张琪,王玉光,周小江,等. 不同地铁车轮结构几何参数下踏面制动热负荷分析[J]. 计算机辅助工程,2016,25(2):19-24.
[10]Newcomb. T. P. Thermal aspects of railway braking[C]. In Proceedings of the IMECHE International Conference on Railway Braking,University of York,1979:7-18.
[11]Balakin. V. A. Heat transfer in friction contact zone at engagement of disc clutches and brakes[J]. Sov. J. Frict. Wear,1997,18(4):450-455.
[12]贾世平. 地铁车辆转向架制动动态温升特性研究[D]. 上海:同济大学,2007.
[13]郑伟生,刘会英. 关于车轮的若干问题及对策[J]. 铁道车辆,1987(1):9-17.
Effect of Slope Length on Braking Thermal Load of Freight Cars
ZHANG Zongwei
( School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract:The special topography and terrain of Sichuan-Tibet Railway cause the length of the ramp to extend along the line. Increasing the length of the ramp will lead to worse braking conditions for freight trains at uniform downhill speed. A three-dimensional finite element model of freight train new wheel is established by ANSYS finite element software. The thermal load of freight train braking at uniform downhill speed is analyzed under different slope lengths with continuous extension of ramp lengths ranging from 10 km to 20 km. The thermal stress field of wheel is calculated by indirect coupling method. The simulation results show the temperature cloud, the thermal stress cloud, and the time history curves of maximum temperature and maximum thermal stress of the new wheel under different slope lengths. It shows that the increase of slope lengths increases the maximum temperature and maximum thermal stress, but the effect decreases gradually. At the same time, by comparing the radial thermal stress of the wheel spoke, we find that the fatigue crack of the plate is prone to occur in the transition corner between rims and spoke plate.
Key words:Sichuan-Tibet railway;tread braking;temperature field;thermal stress
中图分类号:R852.51;U463.53
文献标志码:A
doi:10.3969/j.issn.1006-0316.2020.01.009
文章编号:1006-0316 (2020) 01-0051-06
收稿日期:2019-08-06
作者简介:张宗威(1994-),男,山东枣庄人,硕士研究生,主要研究方向为轮轨关系。

