流域分布式坡长不确定性的初步分析
王 程,陈正江,杨勤科,曹佳云,丑述仁
(西北大学 城市与环境学院,西安7100069)
区域土壤侵蚀调查制图是土壤侵蚀监测和水土保持宏观规划的基础,也是区域尺度土壤侵蚀研究的主要手段。由于区域土壤侵蚀模型尚在研究和开发阶段,因而通用土壤流失方程式(USLE)、修正通用土壤流失方程式(RUSLE)和中国土壤流失方程式(CSLE)等,在大区域土壤侵蚀调查制图中得到了应用[1]。USLE和CSLE中,地形对土壤流失的影响用坡度坡长因子(LS)表示[2-3]。计算流域内各点的LS,是模型应用于流域和区域的关键问题。为此研究者对流域尺度LS因子提取方法进行了一系列的研究,其中包括了对流域分布式坡长提取方法的研究。国外的研究有Hickey和Van Remortel的坡长算法[4-5],国内主要有曹龙熹[6]、张宏鸣[7]、杨勤科[8]和李俊[9]等对流域坡长与LS因子提取方法的研究。由于问题比较复杂,因而已有研究多集中在如何提取坡度坡长并计算LS因子值,而对于坡长的不确定性研究较少。本文从流向算法、分辨率和数据范围三方面对坡长提取的不确定性做出初步分析,以期为区域土壤侵蚀评价提供有力的数据支撑。
1 研究方法
从区域土壤侵蚀研究出发,在水文地貌关系正确DEM(Hc—DEM)的基础上,利用自行开发的LS因子计算工具,分析流域尺度的坡长提取结果的不确定性。
1.1 研究区域及数据基础
1.1.1 研究区 本研究选择典型的黄土丘陵沟壑区——延河流域的二级支流县南沟流域作为研究区。该区面积47km2,土壤侵蚀强烈,侵蚀地貌发育,是研究坡度坡长因子的理想区域。本研究在县南沟流域从流向算法、分辨率和数据范围三个方面进行坡长不确定性分析。通过按流域和行政单元分别进行坡长的提取,来分析数据范围的影响。
1.1.2 数据基础 本研究的数据基础主要为县南沟流域多种分辨率DEM,它是基于1∶1万比例尺地形图(等高线、高程点和水系三个专题层),用ANUDEM建立[10]分辨率分别为5~200m的一系列DEM,分辨率以5m为间隔,设置为5m,10m,15 m,…,195m,200m。
1.2 坡长提取方法
本文只利用经改进的累计径流算法及其相应的工具软件(LS_Tool)[7-8]来提取坡长。坡长提取操作包括:(1)用县南沟流域5m分辨率DEM,用LS_Tool中提供的单流向算法(D8算法)[11]、多流向算法(FD8算法)[12]提取坡长,结果分别称为单流向坡长和多流向坡长,用以比较流向算法对坡长提取结果的影响;(2)利用县南沟流域多种分辨率的DEM,根据单流向算法提取多种分辨率坡长,以分析分辨率对坡长的影响;(3)两种不同数据范围坡长的提取,一是将方塌村包含在内的整个县南沟流域进行坡长提取,裁切后获取方塌村坡长(下文简称为流域范围坡长);二是以方塌村为界,提取坡长(下文简称为村域范围坡长)。假设村界的一部分为分水线、流水线、流水线内和流水线外4种情况(图1),并通过对村界进行一定宽度的缓冲带来消除边界效应。
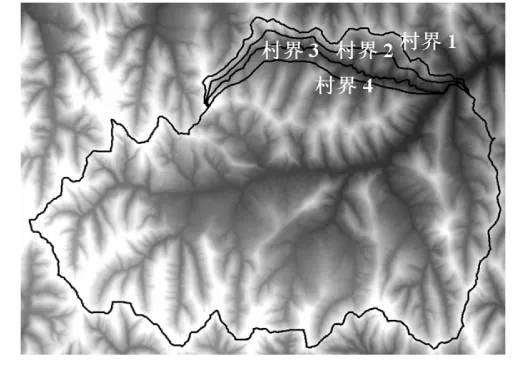
图1 村界图
1.3 坡长分析方法
对于流向算法和数据范围对坡长影响的计算结果,统计其坡长最大值、最小值、均值和标准差,计算坡长频率和累积频率,分析各种提取结果表面特征(空间格局)和统计特征及其与流向算法、分辨率和数据范围的关系。具体研究流程如图2所示。

图2 研究技术流程图
2 结果与分析
从流向算法、分辨率和数据范围三个方面,分析坡长结果的特征。
2.1 流向算法对坡长提取的影响
(1)坡长表面特征。从结果可知,FD8坡长图中短坡长所占的比例很大,主要分布在整个流域的分水线上及山脊处,长坡长主要分布在沟谷,D8坡长也具有基本相同的分布。从两个图的空间格局来看,FD8坡长表面较平滑,与地形关系协调性更好(图3)。

图3 不同流向算法下提取的坡长图(典型区)
(2)坡长统计分布。基于2.5m分辨率DEM提取的结果,单流向坡长与多流向坡长频率存在着较大的差异。多流向坡长分布连续且集中,众数在2.5 m。单流向坡长频率曲线呈锯齿状,众数出现在7 m,频率随坡长增大而变小。在累计频率上占90%面积的坡长值,多流向和单流向分别为21m和95m,说明多流向坡长较短而单流向坡长较长,这种特征从平均坡长上也可看出(图4—5)。
2.2 分辨率对坡长提取结果的影响
统计结果表明(图6—7),随着分辨率的降低,坡长均值和标准差呈线性增加,也就是坡长发生扩张。造成这种结果的原因是分辨率的降低使得DEM表面得到了平滑和概化,部分比较低级别的梁和沟道被忽略,导致坡长值增大[13-14]。

图4 不同流向算法下提取的坡长频率图

图5 不同流向算法下提取的坡长累积频率图
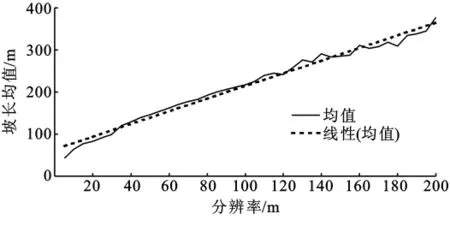
图6 分辨率-坡长均值分布图
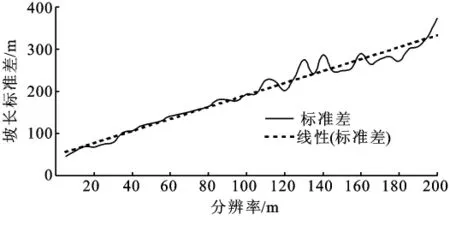
图7 分辨率-坡长标准差分布图
2.3 数据范围对坡长的影响
考虑到LS_Tool中单流向坡度算法比较成熟,本研究先只分析数据范围对单流向坡长的影响。
(1)对村域范围坡长与流域范围坡长进行差值运算,发现4种不同界限的村域范围坡长在其界限边缘都出现异常,在边缘处形成一个误差带。这一异常情况的出现主要原因在于坡长的计算原理是坡面水文学,而径流汇集以流域为单元,起点在分水线上,且水流方向向外,水流方向不正确导致提取的范围坡长产生异常。即使以流域为边界(村界1),也会带来误差。因此,流域分布式坡长的提取,不能简单地以分水线分割的流域为边界。避免的方法是进行界限范围的缓冲。通过对4个村界进行一系列带宽的缓冲试验可得到,当向外缓冲带宽为120m时,它们的边际效应基本得到消除。
(2)按照不同的村界界限提取的村域范围坡长与流域范围坡长之间存在着不同程度的差异,根据D8单流向算法原理,在坡长计算起点统计8个方向的水流流量,以最大水流流量方向作为水流方向来进行坡长累积,若最大水流流向为正东、正南、东南、正西、西南中的其中之一,则水流方向向外,不会影响图1中坡长的累积,提取的坡长正确;若最大水流流量方向为正北、西北、东北中其中之一,水流方向向内,以它或向内某一界限为界进行坡长的提取,会截断坡长的累积,坡长值变小,产生边际效应。根据差值图可以分4种情况(以村界一部分进行讨论)分析范围数据对坡长的影响。
村界位于分水线上(村界1):虽然坡长的计算起点在分水线上,但水流方向向内,截断坡长的累积,坡长值变小,产生较大的边际效应;村界位于流水线上(村界3):坡长计算起点在流水线上,水流方向向外,不影响坡长累积,提取的坡长基本正确;村界位于流水线内侧(村界4):坡长计算起点不在分水线上,但其水流方向向外,不会影响坡长的累积,提取的坡长基本正确;村界位于流水线外侧(村界2):坡长计算起点不在分水线上且水流方向向内,截断坡长的累积,坡长值变小,产生较大的边际效应。由于其坡长计算起点也不在分水线上,因此相比于村界1提取的村域范围坡长,村界2提取的村域范围坡长产生的边际效应更为明显。
3 结论与讨论
(1)不同的流向算法对提取的坡长存在较大影响。单流向算法提取的各长短坡长值所占频率都较小,随着坡长增大,频率有变小的趋势。而FD8算法下,短坡长所占比例大,且多流向算法下求出的坡长值较单流向算法坡长值大。通过比较发现,多流向算法提取坡长更加光滑、连续,更能体现地形凹凸(径流发散、汇集)的影响,与地形关系协调性更好。
(2)基于低分辨率DEM提取的坡长会发生扩张现象,这是由于较低分辨率DEM概化或去除了很多微地形信息,使地形变得平滑,从而导致坡长值增大。
(3)流域分布式坡长提取,必须以向流域外缓冲一定宽度的流域为单元;在本研究条件下,缓冲距离为120m。
(4)不同行政单元界限范围对坡长的影响,主要影响因素是水流方向。若村界位于分水线上且水流方向向外,则提取得到的行政界线范围坡长正确。若村界不在分水线上但水流方向向外,则提取的行政界线范围坡长基本正确。若村界不在分水线上同时水流方向向内,截断坡长的累积,坡长值变小,产生较大的边际效应。因此,坡长的提取应以流域边界或行政单元边界向外缓冲一定宽度为界,避免边际效应的产生。
本研究主要是从各种统计特征值及构造方面对坡长不确定性进行对比分析,因此存在一定局限。下一步工作主要是是利用地统计学方法,通过半变异函数的变化特征来说明空间分布与格局特征。此外,数据范围及其缓冲宽度的建议,仅仅针对黄土丘陵区2.5 m分辨率,更多水土流失区和较低分辨率DEM(如5 m和10m)的情况如何,有待进一步分析。
[1] 杨勤科,李锐,刘咏梅.区域土壤侵蚀普查方法的初步讨论[J].中国水土保持科学,2008,6(3):1-7.
[2] Liu B Y,Zhang K L,Xie Y.A empirical soil loss equation[M].Beijing:Tsinghua press,2002:143-149.
[3] Wischmeier W H,Smith D D.Predicting rainfall-erosion losses from cropland east of the Rocky Mountains:A Guide to conservation planning[M].Washington D C:USDA Agric.Handb,1978.
[4] Hickey R,Smith A,Jankowski P.Slope length calculations from a DEM within ARC/INFO grid[J].Computers,Environment and Urban Systems,1994,18(5):365-380.
[5] Van Remortel R D,Maichle R W,Hickey R J.Computing the LS factor for the Revised Universal Soil Loss E-quation through array-based slope processing of digital elevation data using a C++executable[J].Computers and Geosciences,2004,30(9/10):1043-1053.
[6] 曹龙熹,符素华.基于DEM的坡长计算方法比较分析[J].水土保持通报,2007,27(5):58-62.
[7] 张宏鸣,杨勤科,郭伟玲,等.基于GIS的区域LS因子算法及实现[J].计算机工程,2010,36(9):246-248.
[8] 杨勤科,郭伟玲,张宏鸣,等.基于GIS和DEM的流域坡度坡长因子计算方法[J].水土保持通报,2010,30(2):203-206.
[9] 李俊.基于GIS的小流域坡度坡长因子计算方法研究[D].陕西杨凌:西北农林科技大学,2011.
[10] 张彩霞,杨勤科,段建军.高分辨率数字高程模型构建方法[J].水利学报,2006,37(8):1009-1014.
[11] O’Callaghan J F,Mark D M.The extraction of drainage networks from digital elevation data[J].Computer Vision Graphics and Image Processing,1984,28:323-344.
[12] Freeman T G.Calculating catchment area with divergent flow based on a regular grid[J].Computers and Geosciences,1991,17(3):413-422.
[13] 郭伟玲,杨勤科,程琳,等.区域土壤侵蚀定量评价中的坡长因子尺度变换方法[J].中国水土保持科学,2010,8(4):73-78.
[14] 程琳,杨勤科,谢红霞,等.基于GIS和CSLE的陕西省土壤侵蚀定量评价研究[J].水土保持学报,2009,23(5):61-66.

