淮河流域降雨-侵蚀背景及时空演变特征
马 良,左长清,秦 冰,迟小军
(1.山东省水利科学研究院,济南250013;2.水利部水土保持生态工程技术研究中心,北京100044;3.山东省水利勘测设计研究院,济南250013)
降雨—侵蚀背景是建立土壤侵蚀预报模型的基础及先决条件。深刻理解降雨—侵蚀背景,对提高土壤水蚀预报准确性、提升预报模型精度、评价侵蚀对降雨变化的响应等具有重要的研究价值,并为指导区域水土流失的防治提供科学决策。经验性侵蚀预报模型中普遍认为,在地形、植被等下垫面信息设为常数的前提下,土壤侵蚀可表示成降雨侵蚀力的函数。作为降雨雨强、降雨历时、雨滴质量、直径和速度的复合参数,降雨侵蚀力成为研究降雨—侵蚀背景的特征指标,其代表了降雨引起土壤侵蚀的潜在能力[1-3]。
我国淮河流域地处长江和黄河两流域之间,是我国南北气候过渡带。受夏季季风和地形地貌的影响,流域内降雨具有由南向北递减,山区多于平原,沿海大于内陆,且年际及年内分配极不均匀的特点,从而造成了土壤侵蚀的时空差异。同时,淮河流域内土壤侵蚀对降雨的变化还具有敏感性。因此在水土流失严重及环境敏感的淮河流域开展降雨—侵蚀背景研究,探索背景变化的时间、空间特征,为区域水土保持适应未来气候变化、减少不确定性十分重要。
1 研究方法
1.1 数据来源与预处理
降雨资料来自中国气象科学数据共享服务网提供的中国地面气象资料日值数据集[4]。为消除空间差值客观存在的边界问题,研究中不仅搜集到淮河流域内31个气象站,也包括流域周边72个气象站在内的日降雨数据,通过对站点筛查和缺失数据插补,最终确定了90个有效站点及1951—2008年58a间的降雨序列。
1.2 降雨-侵蚀背景特征要素及计算
降雨侵蚀力是表征降雨—侵蚀背景的经典特征指标,传统可采用EI30公式计算次降雨侵蚀力。但由于很难获取各气象站较长年份的次降雨过程,研究中选择采用气象站常规降雨观测数据建立的简易算法作为计算公式。为保证计算精度,本研究采用以逐日雨量计算年降雨侵蚀力的公式[5]。
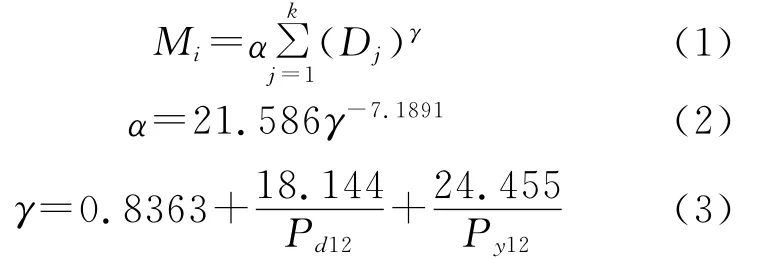
式中:Mi——第i个半月时段的侵蚀力值[(MJ·mm)/(hm2·h)];k——该半月内天数(d);Dj——半月时段内第j天的日降雨量,要求日降雨量≥12mm(与侵蚀性降雨标准对应)(mm);α,γ——模型参数,反映了区域降雨特征,各气象站各不同;Pd12——日降雨量≥12mm的日平均雨量(mm);Py12——日降雨量≥12mm的年平均雨量(mm)。由式(1)—(3)计算出各半月降雨侵蚀力,再求得逐月降雨侵蚀力,累加得到年侵蚀力值。
1.3 时间序列检验方法
研究中采用Mann—Kendall非参数法检验降雨侵蚀力长时间序列的变化趋势。Mann—Kendall检验统计S的计算见公式(4)。
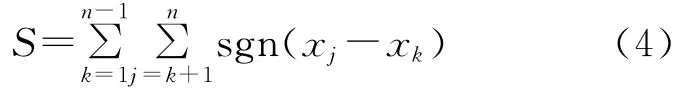
式中:xj,xk——第j年和第k 年代的数值,j>k;n——系列的记录长度(个数);sgn(xj-xk)——返回函数,xj-xk>0时为1,xj-x<0时为-1,xj-x=0时为0[6-7]。
利用统计检验值Zs进行趋势统计的显著性检验;如果︱Zs︱≤Z1-α/2,则接受零假设(无变化趋势),如果︱Zs︱>Z1-α/2,则拒绝零假设。Z1-α/2为标准正态偏量,α为检验的置信水平。Zs的计算见公式(5)。
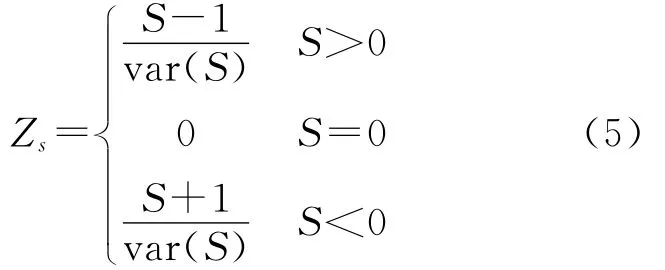
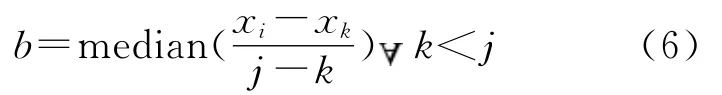
式中:xj,xk——第j年和第k年的数值,如果时间序列长度为n,可以获得N=n(n-1)/2个斜率估计值bi。N个bi的中值就是Kendall倾斜度β值。
1.4 地统计学空间插值方法
研究降雨侵蚀力的区域差异时普遍采用空间插值方法,即利用已知的部分空间降雨侵蚀力样本,对未知空间的侵蚀力信息绘制成图并进行估计。径向基函数(Radial Basis Function,RBF)插值是一种基于地统计学函数的内插方法,主要利用基函数来确定周围已知数据点到内插网格节点的最佳权重,属人工神经网络方法中的一种[9-10]。
是根据基函数类型可划分为多种插值形式,其中常用的是多重二次曲面函数。本文借助ArcGIS 9.3软件提供的RBF法进行空间插值。
Mann—Kendall方法还可用Kendall倾斜度β值来定量计算趋势的幅度[8]。当β为正值时,表示序列为增加趋势;当β为负值时,表示为减少趋势。︱β︱即为趋势的增减幅度。β值的计算如下:首先假设趋势变化是线性的,计算所有序列值对的斜率b:
2 结果与分析
2.1 淮河流域降雨-侵蚀背景分析
经统计计算,淮河流域多年年均降雨量为865.45 mm。如图1a所示,空间分布上呈现由南向北、由东至西递减的特征;南部大别山区是全流域降雨峰值所在,在1 300mm以上,东南部沿海也普遍高于1 000 mm;流域北部降雨量最少,低于600mm。
全流域多年年均降雨侵蚀力,也即降雨—侵蚀背景,为5 269.12MJ/(mm·hm2·h)。与年降水量呈现相似的区域分布特征(图1b),同样以流域南部最高,峰值高于8 000MJ/(mm·hm2·h),东部沿海也普遍在6 000MJ/(mm·hm2·h)以上;但与降雨量不同,流域西部为谷值区域,甚至低于年降雨量最低的流域北部,仅为3 000MJ/(mm·hm2·h)左右,流域北部侵蚀力为4 000~5 000MJ/(mm·hm2·h)。多年年均降雨量与侵蚀力的谷值区域间的差异,可以反映出降雨—侵蚀背景分析是不能用雨量指标简单地进行代替。
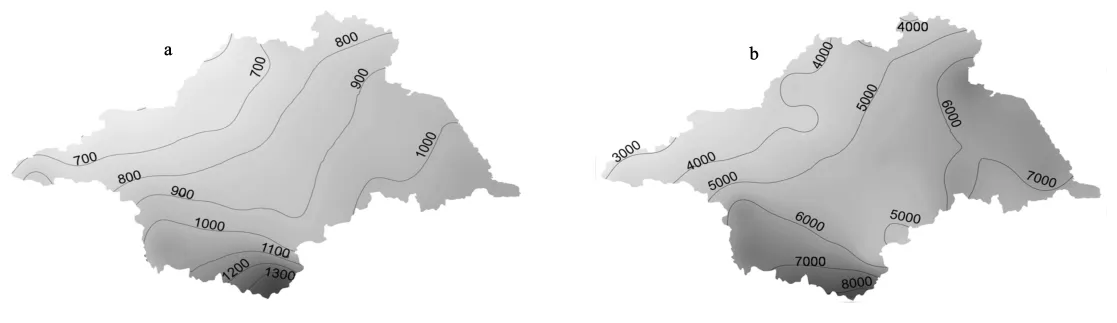
图1 淮河流域多年年均降雨量(a)和多年年均降雨侵蚀力(b)等值线
2.2 降雨-侵蚀背景演变的时间特征分析
图2绘制了淮河流域近60a逐年平均雨量及降雨侵蚀力的演变。线性趋势分析表明,降雨雨量与侵蚀力呈现正相关关系,谷值均出现在1965年,峰值则分别出现在2003年和1956年。但经Mann—Kendall非参数法检验认为,在1951—2008年间淮河流域内年降雨雨量及年侵蚀力未呈现显著增减变化。
虽然全流域各气象站平均的降雨—侵蚀背景的年值序列未显现增减变化,但并不能掩盖单个气象站可能存在的演变趋势。单个站点上降雨—侵蚀背景的演变趋势及空间特征,对了解区域降雨潜在侵蚀之间的差异具有更重要的意义。
2.3 降雨-侵蚀背景演变的空间特征分析
研究流域内降雨—侵蚀背景演变的空间特征,首先采用Mann—Kendall法对单个气象站的降雨量、侵蚀力年序列分别进行趋势检验,提取检验结果为显著气象站的定量趋势(即Kendall倾斜度β值),然后利用径向基法对β值进行空间插值,最后用淮河流域的边界进行提取,得到降雨量、降雨侵蚀力演变趋势的空间特征图(图3a、图3b)。
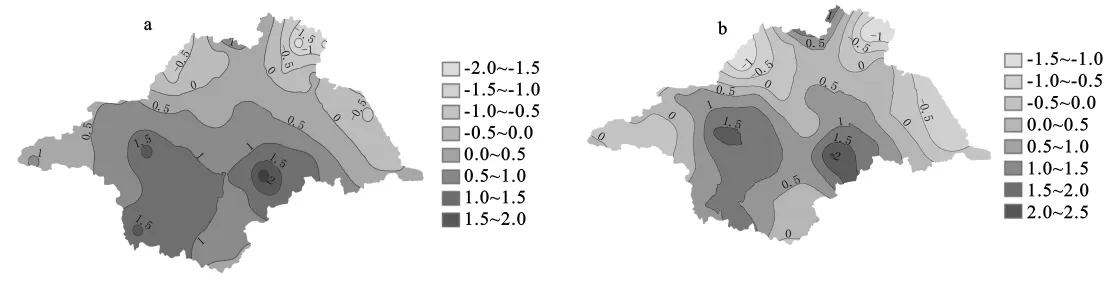
图3 淮河流域降雨量(a)和降雨侵蚀力(b)β等值线
淮河流域近60a雨量演变趋势的区域差异性显著,如图3a所示。全流域有三个显著上升中心,分别位于周口附近、桐柏山以及蚌埠附近,上升幅度即︱β︱均在1.5以上;另在流域北部受鲁中南低山丘陵区上升趋势的拉动作用[11],也呈现显著的上升趋势。在流域东部沿海地区,如盐城及沂沭河水系附近呈现显著下降趋势。
如图3b所示,降雨—侵蚀背景演变的空间分布趋势与雨量略有不同。流域中部周口附近上升中心、蚌埠上升中心的面积均显著加大,桐柏山上升中心向东南转移至大别山区;流域北部鲁中南低山丘陵沿脉区域的上升趋势更为明显。除流域东部沿海地区仍存在显著下降趋势外,山东南四湖附近及黄泛平原的降雨侵蚀力呈现下降趋势的面积显著扩大。
3 结论
本文提出以降雨侵蚀力为表征降雨—侵蚀背景的指标,对淮河流域近60a降雨—侵蚀背景演变的时间、空间特征进行了分析。综合研究认为,淮河流域多年年均降雨侵蚀力为5 269.12MJ/(mm·hm2·h),峰值分布在流域南部的大别山区,而谷值区域为流域西部。借助Mann—Kendall非参数检验,1951—2008年间全流域内降雨—侵蚀背景未呈现显著增减趋势。
研究中还得到,近60a间淮河流域内周口、大别山区以及蚌埠附近三个地区的降雨侵蚀力呈现显著上升趋势,北部鲁中南低山丘陵沿脉区域也呈现出一定上升趋势,也即上述地区的降雨—侵蚀背景逐渐增强。由于这里分布有国家级水土流失重点预防保护区(桐柏山—大别山区)、重点治理区(沂蒙山区)、主要的省级水土流失重点监督或治理区(如安徽省蚌埠南部等),因此以上区域应优先加强土壤侵蚀防治对未来降雨变化的适应研究。
[1] Morgan R P C.Soil erosion and conservation[M].Oxford:Blackwell Publishing,2005:45-50.
[2] Brown L C,Foster G R.Strom erosivity using idealized intensity distributions[J].Transactions of the American Soci-ety of Agricultural Engineers,1987,30(2):379-386.
[3] Van Dijk A I J M,Bruijnzeel L A,Rosewell C J.Rainfall intensity-kinetic energy relationships:a critical literature review[J].Journal of Hydrology,2002,261(1/4):1-23.
[4] 中国地面气象资料日值数据集[R/OL].[2011-07-05].http:∥cdc.cma.gov.cn/shuju/index3.jsp?tpcat=SURF&dsid=SURF_CLI_CHN_MUL_DAY
[5] 章文波,付金生.不同类型雨量资料估算降雨侵蚀力[J].资源科学,2003,25(1):35-41.
[6] Yue S,Pilon P,Cavadias G.Power of the Mann-Kendall and Spearman′s rho tests for detecting monotonic trends in hydrological series[J].Journal of Hydrology,2002,259(1/4):254-271.
[7] Burn D H,Burn M A,Hag E.Detection of hydrologic trends and variability[J].Journal of Hydrology,2002,255(1/4):107-122.
[8] Xu Z X,Takeuchi K,Ishidaira H.Monotonic trend and step changes in Japanese precipitation[J].Journal of Hydrology,2003,279(1/4):144-150.
[9] Lukaszyk S.A new concept of probability metric and its applications in approximation of scattered data sets[J].Computational Mechanics,2004,33(4):299-304.
[10] 魏义坤,杨威,刘静.关于径向基函数插值方法及其应用[J].沈阳大学学报,2008,21(1):7-9.
[11] 马良,左长清,尹忠东,等.山东省降雨侵蚀力多年变化特征分析[J].中国水土保持科学,2010,8(4):79-85.

