基于不同分辨率DEM提取坡长的统计分布
郭伟玲, 樊 宇, 杨勤科
(1.安徽理工大学 测绘学院, 安徽 淮南 232001; 2.西北大学 城市与资源环境学院, 西安 710127)
分布式侵蚀学坡长(简称坡长)[1]是指在土壤侵蚀过程中具有累积和截断特征的坡长,该坡长通常在两种情况下截断:一是在坡度大幅度变缓而发生沉积时,称为坡度截断;二是在清晰可辨的沟道或者河网处坡面漫流结束而发生截断,称为沟道截断[2]。这一概念在土壤侵蚀研究中被广泛使用[3-5]。
不同分辨率的数字高程模型(Digital Elevation Model,DEM)多基于相应比例尺地形图插值生成[6],目前主要是通过不同的数据采集方式,得到不同分辨率;如三维激光扫描得到亚米级、Lidar得到米级等。因此地形图的制图综合、采集方式以及数据组织方式[7]、DEM内插方法[8]等因素无疑会影响到基于DEM提取的地形因子如侵蚀学坡长的精度[9],并存在着复杂的不确定性[10]。此外流向算法、数据边界、坡长截断方式等,都影响着坡长提取的结果。
坡度和坡长是影响土壤侵蚀的最主要地形因子,也是水土流失评价中的重要指标。陈楠[11]、汤国安[12]、刘红艳[13]、王春梅[14]等许多学者对坡度与DEM分辨率之间的关系进行了一系列研究。郭伟玲等[15]和王程等[16]的研究表明随着DEM分辨率的增加,许多地形细节被概括,DEM将逐渐不能表达真实地表起伏情况,其上提取的坡度值变小,坡长值增大。秦伟等在坡长因子研究进展中对坡长因子研究提出了展望,其中包括提取算法、地貌地形、DEM分辨率等因素对坡长提取的影响[17]。关于坡长提取结果随分辨率变化的研究相对较少,坡长同样是影响土壤侵蚀的另一重要地形因素[18],因此在水土保持研究工作中也迫切需要能够提供准确的坡长信息。
本研究基于前人的研究成果[15,19],结合信息论和地统计学等理论[20]探讨侵蚀学坡长随DEM分辨率变化的规律并对其进行定量表述,以期为选取合适的DEM分辨率计算坡长提供技术支持。
本文以1∶10 000比例尺地形图生成的2.5 m分辨率DEM所提取的坡长为真值,对比不同分辨率DEM上提取的坡长与真值的误差并观察分级坡长区随分辨率变化的规律,计算误差与分辨率之间的数学关系,总结经验公式,并将经验公式在检验样区进行检验。研究将为水土保持工作中选取合适的DEM分辨率提供科学依据。
1 研究方法
1.1 研究样区与数据源
本研究选用两个研究样区,试验样区位于陕西省安塞县县南沟流域,检验样区位于陕西省绥德县韭园沟流域。两个研究样区均为地形变化复杂、水土流失严重的黄土丘陵沟壑区,这里沟壑纵横,地貌变化起伏无常,是土壤侵蚀较为严重的区域,也是水土保持研究工作的重点区域,图1为研究区的DEM示意图。
两个样区的数据均采用由国家测绘部门编制的1∶10 000比例尺的数字线画图(Digital Line Graphic,DLG,等高距均为5 m)经过必要的查错、编辑处理后作为本研究的数据源。
图1 研究区DEM
1.2 多尺度DEM生成及坡长提取方法
计算分布式侵蚀学坡长时,主要有单流向和多流向两种流向算法可供选择。单流向算法以单个格网单元为中心向周围流出,共有8个水流方向(即正方形的对角线和中线方向),但该格网单元的水流只能流入与之相邻的一个格网单元,而不分配流量。考虑到水流的发散性,给定格网单元的水流应该是结合坡度、坡向等因素分配流量后流入相邻的多个格网单元,所以本研究计算侵蚀学坡长采用基于坡度的多流向算法MS[21]。
本文使用1∶10 000比例尺DLG数据作为建立DEM的基本信息源,经专业DEM插值软件ANUDEM[22]多次插值生成2.5 m(最佳分辨率)[23]和10~200 m间隔10 m的不同分辨率的DEM数据。再通过LS_TOOL工具[24]分别对上述DEM数据提取多流向分布式土壤侵蚀学坡长。
1.3 坡长信息提取
基于统计学原理,结合之前的研究经验[25],坡长表面的坡长值分布呈多态和偏态现象,不符合正态分布。本研究将2.5 m分辨率坡长图进行自然对数计算,使其符合正态分布,再将其进行等间距划分,共划分成8个区间。对区间阈值进行反函数计算使其转换成坡长值,据此来划分出8个坡长分级,分级方案见表1。通过改变DEM分辨率,观察不同级别坡长面积占坡长总面积的比值随DEM分辨率变化规律。
表1 坡长分级方案
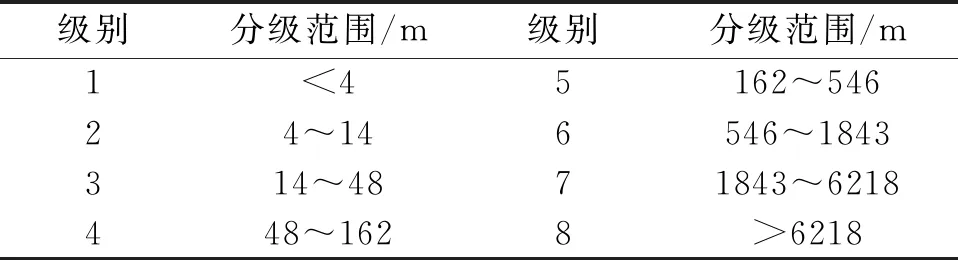
级别分级范围/m级别分级范围/m1<45162~54624~146546~1843314~4871843~6218448~1628>6218
2 结果与分析
2.1 DEM分辨率对坡长的影响
研究应用LS_TOOL软件[24]提取多流向土壤侵蚀学坡长,以研究区最佳分辨率2.5 m的DEM提取的坡长为基准值,结合研究特点制定分级方案(表1 )对2.5 m和10~200 m的坡长表面进行分级,计算得到不同坡长级别占坡长总面积的比率随分辨率变化趋势图(图2)。
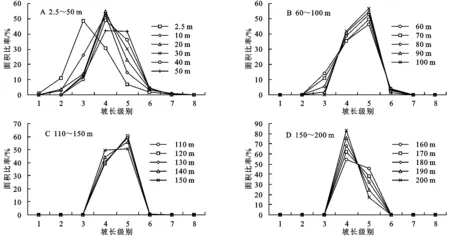
图2 不同分辨率DEM提取坡长分级面积曲线对比
观察图2可以看出,坡长总体取值范围随着分辨率变粗而缩小,即值域变窄,坡长面积分布逐渐向第4,5级过渡并集中,对2.5~150 m的坡长最大表面积所在级别进行统计并计算众数,发现众数为5,说明坡长表面积最终集中分布于第五级别范围内,尤其是分辨率大于90 m后。这说明随着DEM分辨率降低而产生制图综合作用,细小沟道被忽略,导致其上提取的短坡长合并变长,坡长值向较高级别区域扩张,短坡长面积比率逐渐趋于零,同时6~8级别坡长面积比率也呈现出相同的变化,到100 m分辨率时几乎为零。因此随着分辨率降低坡长面积比率曲线的峰值逐渐右移,呈现出2.5~50 m时向第4级别集中,60~140 m向第5级别集中,对比图2C和2D可以发现分辨率150~200 m时峰值部分又向第4级别集中,当分辨率为200 m时第4级别面积比率达到0.83,总体上坡长集中分布在4,5级别内。综上所述DEM分辨率对不同坡长级别的影响变化是不同的。
从图2B中还可以发现,坡长的1~3级别和6~8级别坡长衰减并向中等坡长区转化,导致4~6级别坡长所占面积的增加,其中短坡长部分的减少是由于坡长算法所导致的,坡长最小值基本为对应分辨率的一半,随着分辨率的降低坡长最小值必然变大,短坡长区也相应减少。可见分辨率的降低会造成短坡长区缩小并向中等坡长区延伸,长坡长区面积先增加后减少的现象。
将图2所对应的数据排列成每行为不同级别的坡长面积(1~8级别,共8行),每列为不同分辨率(2.5~200 m,共21列),进行列与列之间的相关性分析,得到相关系数矩阵,提取各分辨率与2.5 m分辨率坡长分级的相关系数,按顺序做成相关系数变化图,据此来说明各分辨率坡长分布特征与基准分辨率之间的变化相似性,见图3。
从图中可以看出120 m分辨率是一个突变点,120 m分辨率之前各分辨率坡长分布特征与基准分辨率的相关系数是下降的,之后略有上升。说明120 m分辨率下坡长分布特征变化与2.5 m相似性最低,变化较2.5 m有显著差异。
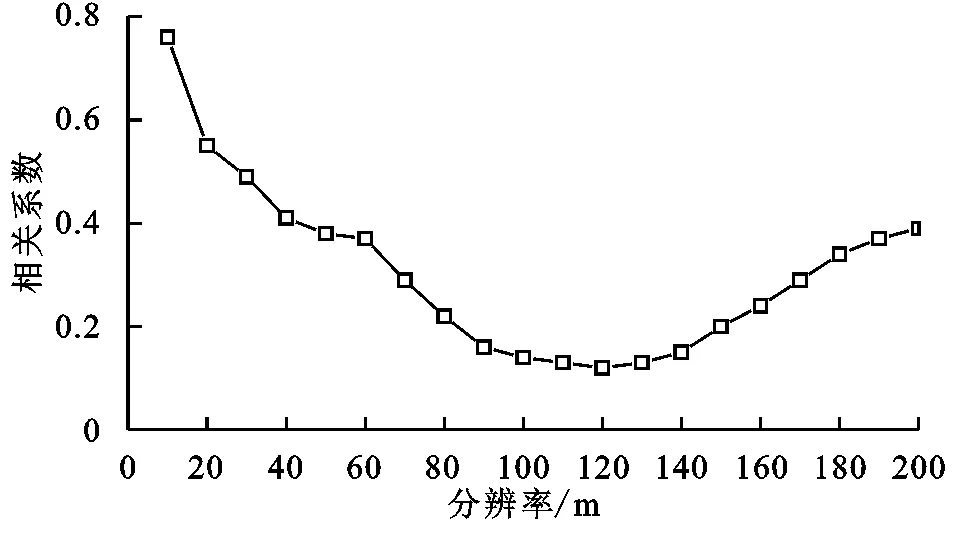
图3 相关系数变化
从统计学指标和信息论中信息熵概念[17]来总体分析分辨率对坡长提取的影响,见表2。
从表2可以看出,随着分辨率降低,坡长面积标准差总体上呈增大趋势,由此可见在分辨率降低过程中,即有效栅格尺寸增大,地表起伏被概括表达,坡长趋于扩张并且集中程度增加。标准峰度系数总体上随分辨率降低而增大,表明坡长面积比率曲线在低分辨率时要比高分辨率陡峭,分辨率在50 m和150 m时标准差分别出现一个低值,表明此时坡长分布集中程度要低于相邻分辨率,结合图2可以发现50 m和150 m正是坡长面积比率开始向另一级集中的拐点,随后集中程度开始攀升,这说明分辨率对坡长分布的影响是分段变化的,坡长面积比率曲线总体上变的更加陡峭,比正态分布更加集中。从坡长表面信息熵来看,2.5 m到40 m坡长表面信息熵是增大的,说明坡长表面随分辨率降低而变得更加离散。分辨率自40 m之后坡长表面信息熵呈现单调递减趋势,这是由于坡长分布趋于集中,短坡长区(1,2,3)和长坡长区(6,7,8)面积减少为零而引起的,与前述坡长面积曲线分析结果相互应证。
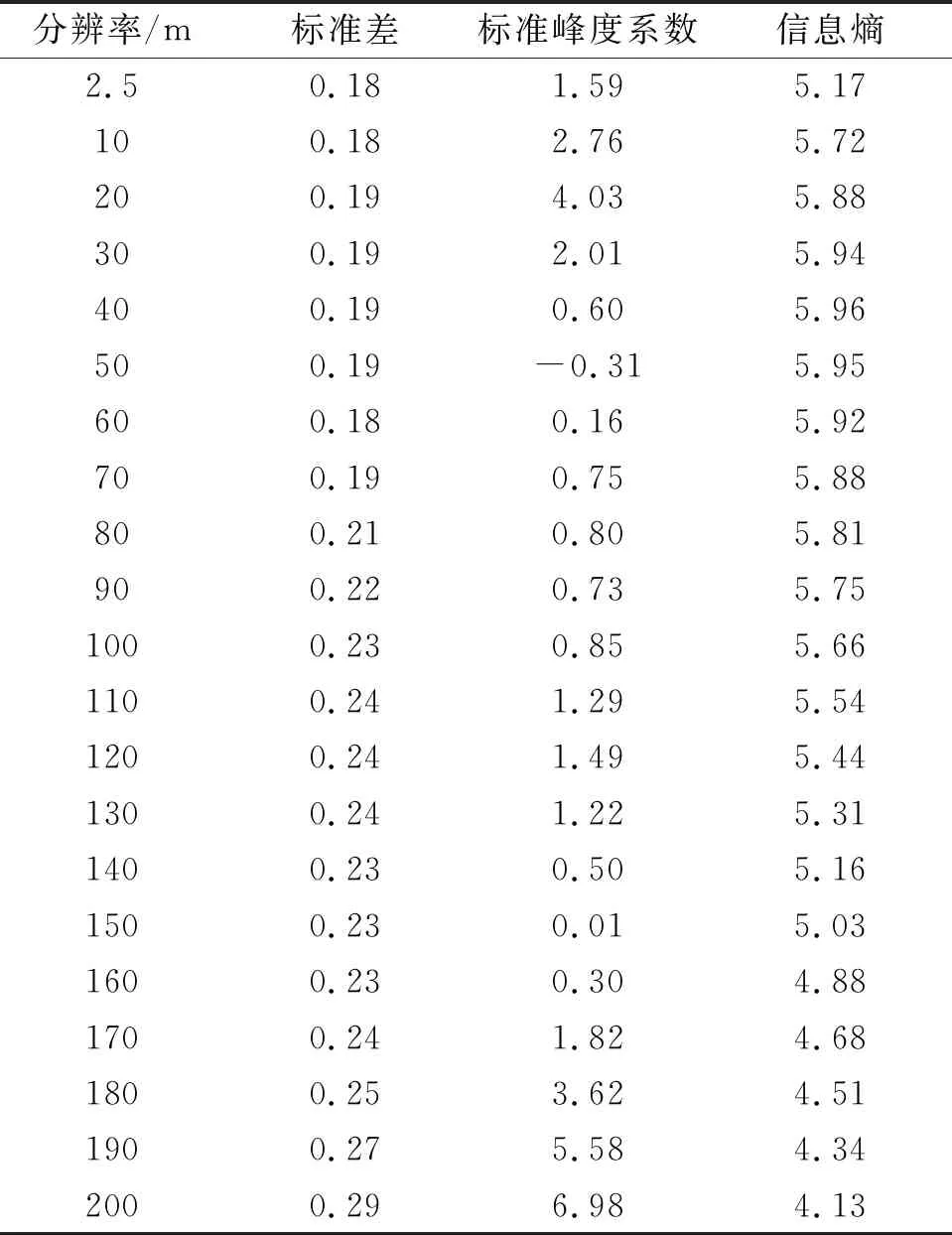
表2 不同分辨率坡长表面统计信息
对不同分辨率坡长信息熵进行拟合,得到公式(1):
y=-0.00009x2+0.01208x+5.451R2=0.9586
(1)
式中:y为坡长信息熵;x为DEM空间分辨率(m)。对(1) 式两边求导则有:
y′=-0.00018x+0.01208
(2)
根据导数的定义可知y′即为DEM分辨率造成的坡长表面分布变化的定量表述,因此式(2)可以作为县南沟流域1∶10 000比例尺下DEM分辨率对其提取坡长不确定影响的定量公式,用来衡量该比例尺下不同分辨率对坡长提取的不确定性影响程度。
2.2 坡长分布与DEM分辨率的函数关系
前面分析了不同坡长级别的面积变化特征,接下来需要找出一个指标来衡量不同分辨率的坡长误差大小,并求出误差与分辨率的函数关系。通过该函数的反函数即可根据误差精度的需要来求得适宜的DEM分辨率参数,这对提取坡长时选择合适的DEM分辨率,避免分辨率选取的任意性,保证坡长提取精度需求等具有一定意义。
以不同分辨率中各级别坡长面积相对于最佳分辨率中对应级别的坡长面积差值绝对值作为坡长的绝对误差。随后将绝对误差除以2.5 m分辨率坡长表面积作为相对误差,再根据2.5 m坡长表面积进行加权得到加权总体误差。计算公式如下:
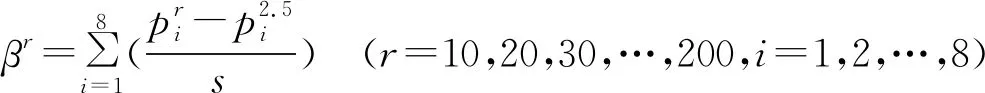
(3)
式中:βr为加权总体误差;p为坡长面积,上标r表示分辨率,下标i表示坡长级别;s为研究区总面积。
通过上述公式对试验数据计算结果见图3。对图3中的拟合函数求其反函数则可以得到公式:
r=10e4.72βr-3.19
(4)
式中:r为DEM分辨率;βr为误差大小。这样我们就可以根据坡长提取精度要求,即坡长加权总体误差大小,通过公式(4)来求得适宜的DEM分辨率。
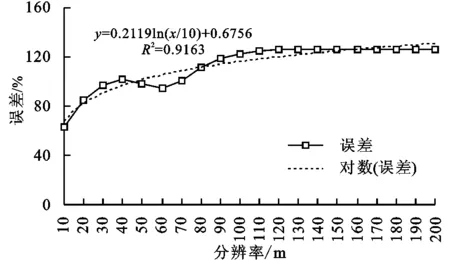
图4 误差与分辨率关系
2.3 模型检验
选取陕西绥德韭园沟流域作为检验样区,取加权总体误差0.5~1.5,根据公式(4)求得所需要的DEM分辨率,再根据求得的分辨率在检验样区建立相应的DEM并提取坡长,根据公式(3)计算实际加权总体误差,并求出所取误差与实际误差之间的绝对差值,见表3。
表3说明根据实际工作需要控制选取误差,并利用公式(4)求得对应分辨率DEM,在其上提取的坡长实际加权总体误差仍然非常接近公式计算中代入的选取误差βr,这表明此公式同样适用于其他黄土丘陵沟壑样区。
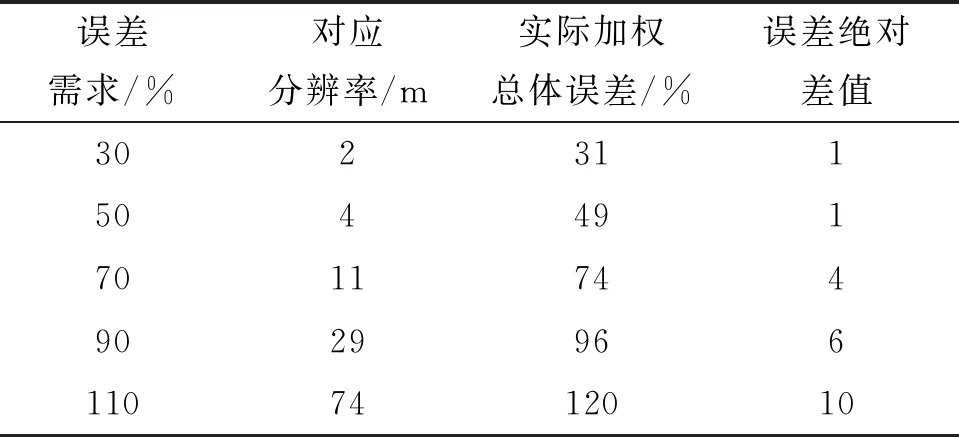
表3 模型检验误差对照
3 结 论
(1) DEM空间分辨率降低会导致坡长分布情况变化,表现为不同分辨率对坡长各个分级区的影响是不同的,变化规律为短坡长区和长坡长区均减少并向中等坡长区集中。
随着分辨率降低,坡长趋于扩张并且集中程度增加,此外分辨率对坡长分布的影响是分段变化的。
(2) 本文通过试验得出了由DEM分辨率降低而导致坡长表面变化的定量表述公式。通过对不同分辨率提取坡长的误差计算,用加权总体误差这一指标来衡量不同分辨率的坡长误差大小,并得出其与DEM分辨率的函数关系,通过该函数的反函数即可根据误差精度的需要来求得适宜的DEM分辨率参数。通过试验样区检验该经验公式,效果良好。
由于检验样区同为黄土丘陵沟壑区且样本量较小,今后的研究还可以继续深化,如采用不同地貌类型区,不同范围的研究区来探索经验公式,也可以结合地形图比例尺,地貌差异等多种因素来探讨。

