基于有限元法的电力巡线机器人机械结构动态特性分析

文广，苏睿，姚锟，吴学峰，惠重粒

基于有限元法的电力巡线机器人机械结构动态特性分析

文广1，苏睿1，姚锟1，吴学峰2，惠重粒2

（1.成都工业学院 智能制造学院，四川 成都 611730；2.成都天可精创科技有限公司，四川 成都 610041）

电力巡线机器人往往工作在距地数十米的高空，经常承受随机性的风载荷，其机械结构的动态特性对其动态响应影响较大。以某轮飞式电力巡线机器人为研究对象，利用有限元软件，对其动态特性进行分析，通过分析获取结构的固有频率、振型等动态特性参数。分析结果表明：该机器人机械结构在约束状态下的前6阶固有频率分别为：4961.1 Hz、19722 Hz、29702 Hz、94488 Hz、121190 Hz、161450 Hz，各阶模态振型表现为：第1、5、6阶为结构绕轴的摆动振型，第2阶为结构绕轴的摆动振型，第3、4阶为结构绕轴的摆动振型，其中第4、6阶模态对结构动态特性的影响最大。分析结果为该机器人机械结构的动态优化提供了理论基础。

电力巡线机器人；模态分析；谐响应分析；固有频率；振型

高压输电线路一般架设在户外距地数十米的高空中，所处环境比较恶劣，易出现散股、线路老化、破损、金具脱落等问题，因此，需要定期巡检[1]。高压输电线路的巡检工作一般有三种方式：人工巡检、直升机或无人机巡检、机器人巡检。相对而言，人工巡检效率低，且危险程度高，无人机或直升机巡检则费用高，因此，采用机器人巡检是目前比较普遍的线路巡检方式。设计开发方便实用的高空输电线路巡检机器人成为了各国相关机构的研究热点。早期的线路巡检机器人系统比较简单，仅仅能完成两座线塔之间的巡检作业，且工作时需要人工辅助[2]。国外研究线路巡检机器人的时间相对较早，如日本研制出了架空地线上作业巡检机器人（OPGW）[3]、伊朗研制出了高压线检测机器人[4]等，国内也在20世纪90年代开始了相关的研究工作，如上海大学研制出了高压导线巡检机器人[5]、沈阳航空航天大学研制出了模块化轮指式高压线巡检机器人[1]等。机械结构是输电线路巡检机器人的核心部件，其工作可靠性直接影响着机器人的巡检工作性能。也有部分研究人员针对线路巡检机器人的机械结构开展了设计工作。周俊等[6]专门为高压线路巡检机器人设计了一种越障机构，该机构由曲柄滑块机构、摆动导杆机构和槽轮机构组成。姜生元等[7]则为了解决吊臂巡线机器人跨越线缆时出现的姿态失稳问题而设计了一种自平衡机构。对输电线路巡检机器人来说，工作时承受的载荷往往是随机的动态载荷，其结构动态特性对动态响应影响较大，因此，在设计机器人机械结构时，非常有必要对其动态特性进行研究。目前，大部分的设计人员都将结构运动学或动力学特性[8-10]作为其研究方向，较少关注结构的模态振型等动态特性参数的研究。本文以某轮飞式电力巡线机器人为研究对象，利用有限元软件，对其动态特性进行分析，通过分析获取结构的固有频率、振型等动态特性参数，

并考察对结构动态特性影响较大的模态。研究结果为该机器人机械结构动态特性的优化提供了理论基础。

1 机器人机械结构示意及有限元模型

本文研究的电力巡线机器人主要通过最上方的两个车轮与输电线路接触来实现沿线路方向的移动。整机结构使用铝合金制成，表1给出了该材料的性能参数。分析前，在有限元软件中建立结构的有限元模型，由于模型为不规则结构，因此，采用solid187单元来模拟，并使用自由网格划分方式对其进行网格划分，该有限元模型共有252702个单元、359752个节点。图1给出了该电力巡线机器人机械结构的有限元模型。

表1 铝合金材料性能参数

图1 机器人机械结构有限元模型

2 机器人机械结构模态分析

模型建立后，采用兰斯索斯法[11]，对其进行约束状态下的模态分析[12]，分析后提取结构的固有频率和振型。根据实际工作状态对模型进行约束，该输电线路检测机器人在巡线时主要依靠上方的轮子在电线上行走，因此，本文分析时选择约束轮子（如图1所示）与电线接触部位的所有平动自由度。根据模态理论，对结构动态特性影响较大的是低阶模态，因此，本文只提取了该输电线路检测机器人的前6阶模态。该机器人机械结构的前6阶固有频率如表1所示，图2给出了结构的前6阶模态振型。

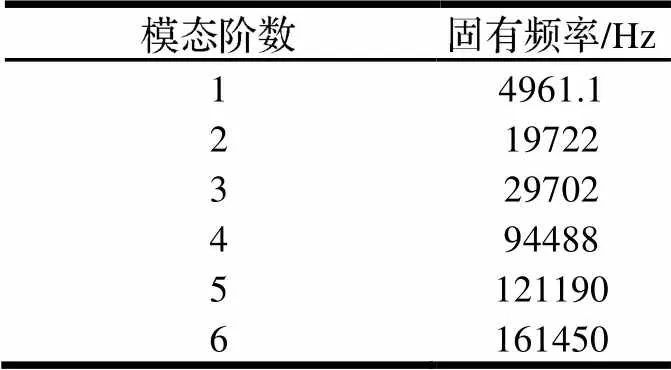
表2 电力巡线机器人机械结构模态固有频率

图2 电力巡线机器人机械结构模态振型

从图2可以看出，该机器人机械结构的前6阶模态振型表现如下：第1、5、6阶为结构绕轴的摆动振型，第2阶为结构绕轴的摆动振型，第3、4阶为结构绕轴的摆动振型。

3 机器人机械结构谐响应分析

为了进一步分析对结构动态特性影响最大的模态，对该电力巡线机器人机械结构进行了简谐振动响应分析。从模态分析结果可知，该机器人机械结构的前6阶固有频率最大值为161450 Hz，因此，在进行简谐振动响应分析时，将激励频率范围设置为0～165000 Hz，分成33份，载荷大小设置为阶跃载荷，即考虑结构在载荷大小保持不变时的响应。该输电线路检测机器人在工作时主要承受自身的重力，因此，本文仅研究结构在重力载荷下的位移响应。通过分析，提取结构上部分关键节点的位移幅值随激励频率的变化曲线如图3所示。

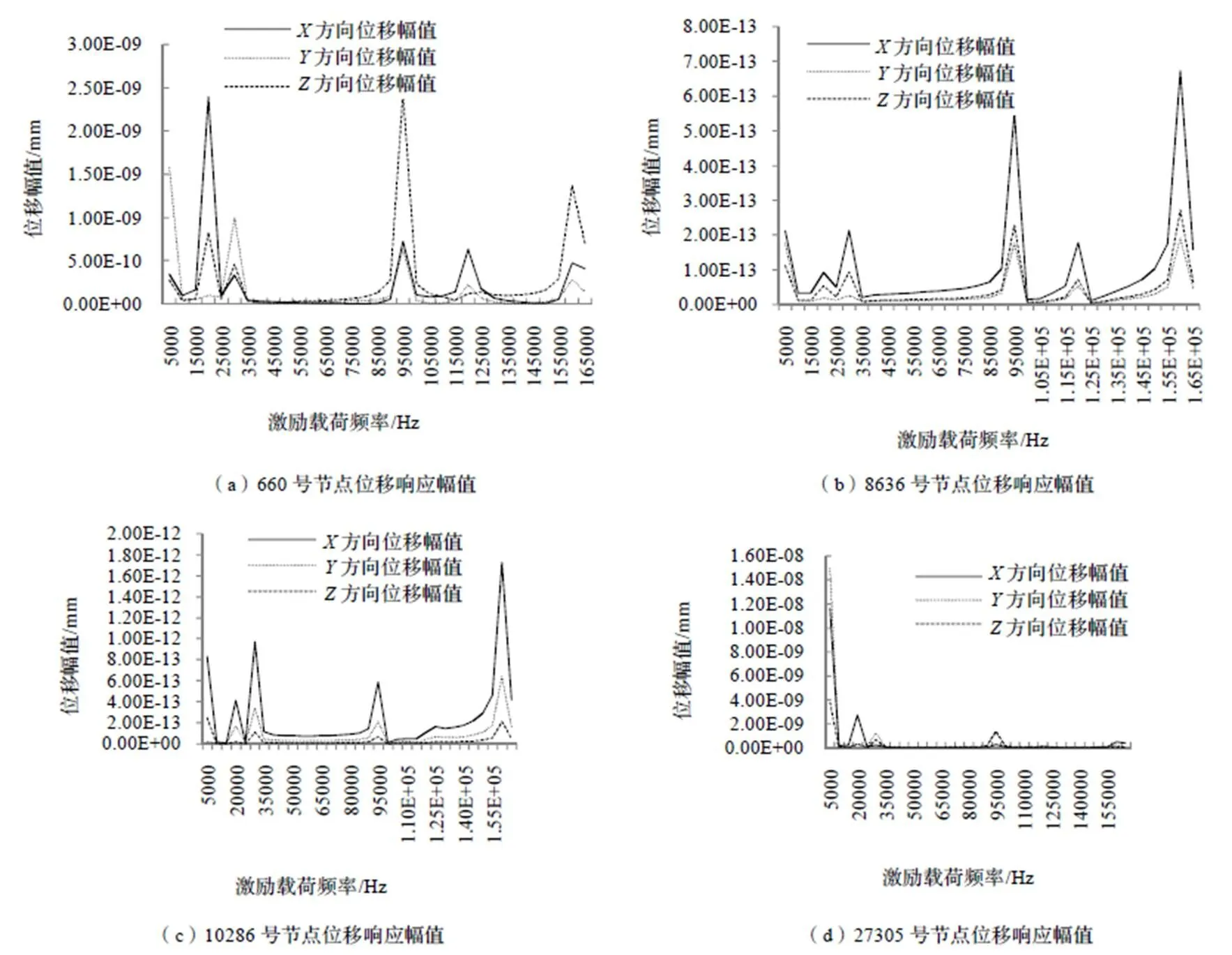
图3 关键节点的位移幅值随激励频率的变化曲线

从图3（a）可以看出，在不同激励频率的简谐载荷作用下，660号节点的、、三个方向的振动位移幅值均在激励频率为5000 Hz、20000 Hz、30000 Hz、95000 Hz、120000 Hz、160000 Hz时出现了峰值，其中，峰值较大值出现在激励频率为20000 Hz和95000 Hz时。从图3（b）可以看出，8636号节点在不同激励频率的简谐载荷作用下，其、、三个方向的位移幅值变化曲线也出现了明显的峰值，且峰值出现在激励频率为5000 Hz、20000 Hz、30000 Hz、95000 Hz、120000 Hz、160000 Hz时，当激励频率为95000 Hz和160000 Hz时，其峰值较大。从图3（c）可以看出，10286号节点的各方向位移幅值变化曲线表现规律和660、8636号节点相似，同样，其、、三个方向位移幅值变化曲线均出现了明显的峰值，峰值出现在激励频率为5000 Hz、20000 Hz、30000 Hz、95000 Hz、120000 Hz、160000 Hz时，当激励频率为30000 Hz和160000 Hz时，其峰值较大。从图3（d）可以看出，27305号节点的、、三个方向的振动位移幅值均在激励频率为5000 Hz、20000 Hz、30000 Hz、95000 Hz、160000 Hz时出现了峰值，当激励频率为5000 Hz时，其峰值最大。

综合来看，当激励频率值为20000 Hz和95000 Hz时，660号节点的位移响应幅值变化曲线峰值较大，而8636号节点的位移响应幅值变化曲线较大峰值出现在了激励频率为95000 Hz和160000 Hz时，10286号节点的位移响应幅值变化曲线较大峰值出现在了激励频率为30000 Hz和160000 Hz时，27305号节点的位移响应幅值变化曲线较大峰值出现在了激励频率为5000 Hz时。从上述分析结果来看，激励频率分别为95000 Hz和160000 Hz的载荷对机器人机械结构的振动响应影响相对更大，从模态分析结果可知，结构的第四阶模态频率与95000 Hz接近，第六阶模态频率与160000 Hz接近，因此，可以认为，对结构动态特性影响最大的的是第四阶模态和第六阶模态。

4 结论

本文利用有限元软件，对某轮飞式电力巡线机器人机械结构进行动态特性分析，通过分析得出如下主要结论：

（1）该机器人机械结构的前6阶模态固有频率分别为：4961.1 Hz、19722 Hz、29702 Hz、94488 Hz、121190 Hz、161450 Hz。

（2）该机器人的第四阶和第六阶模态对结构自身的动态特性影响较大，在后续优化设计过程中需要重点考虑这两阶模态的影响。

[1]叶长龙，闫法兵，姜春英，等. 模块化轮指式高压线巡检机器人[J]. 沈阳航空航天大学学报，2018，35（2）：28-34.

[2]DEBENEST P，GUAMIERIM，TAKITA K，et al. Ex-pliner-Robot for inspection of transmission lines [C]. International Conference on Robotics and Automation，2008：3978- 3984.

[3]SAWADA J，KUSUMOTO K，MUNAKATA T，et al. A Mobile Robot for Inspection of Power Transmission Lines[J]. IEEE Transactions on Power Delivery，1991，11（1）：57.

[4]MOSTASHFI A，FAKHARI A，BADRIM A. A novel design of inspection robot for high-voltage power lines[J]. Industrial Robot，2014，41（2）：166-175.

[5]ZHIBIN R，YI R，YONG Y，et al. Control of inspection robot for the power transmission lines based ondatabase[C]. 27th Chinese Control Conference. IEEE，2008：281-285.

[6]周俊，冷鸿彬，朱洪俊. 高压线巡检机器人越障机构设计[J]. 机械设计，2012，29（12）：25-27.

[7]姜生元，任立敏，焦宏章，等. 吊臂式巡线机器人悬吊姿态自平衡机构的研究[J]. 机械设计，2011，28（1）：49-52.

[8]王吉岱，张彦囡，甄静. 高压线路巡检机器人机械臂闭链机构的运动学分析[J]. 机床与液压，2018，46（11）：41-45.

[9]王海峰，李凤婷，贾言争，等. 适用于大规模光伏阵列的无水清扫机器人[J]. 可再生能源，2015，33（10）：1439-1444.

[10]封尚，章合滛，薛建彬，等. 线缆巡线机器人机械结构设计及动力学分析[J]. 机械与电子，2013（12）：70-74.

[11]张朝晖. ANSYS 12.0结构分析工程应用实例解析[M]. 3版. 北京：机械工业出版社，2010．

[12]王德民，别磊，姜俊霞，等. 工业机器人RV减速机摆线轮模态分析[J]. 机械，2019，46（6）：60-65.

Dynamic Characteristics Analysis of Mechanical Structure of Electric Patrol Robot Based on Finite Element Method

WEN Guang1，SU Rui1，YAO Kun1，WU Xuefeng2，HUI Chongli2

( 1.School of Intelligent Manufacturing, Chengdu Technological University, Chengdu611730, China; 2.Chengdu Tianke Jingchuang Technology Co., Ltd., Chengdu610041, China)

Electric patrol robot often works tens of meters above the ground and bears random wind loads, and the dynamic characteristics of the mechanical structures have a great impact on their dynamic response. This paper studies a flying electric patrol robot. The dynamic characteristics of the robot are analyzed by using finite element software, and the natural frequencies and vibration modes of the structure are obtained through analysis. The results show that the first six natural frequencies of the mechanical structure are 4961.1, 19722, 29702, 94488, 121190 and 161450 Hz, respectively. In the first, fifth and sixth order, the swing modes of the structure are aroundaxis. In the second order, the swing modes of the structure are aroundaxis, and in the third and fourth order, the swing modes of the structure are aroundaxis. Among them, the fourth and sixth modes have the greater influence on the dynamic characteristics of the structure. The analysis results provide a theoretical basis for the dynamic optimization of the mechanical structure of the robot.

electric patrol robot；modal analysis；harmonic analysis；natural frequencies；vibration type

TP242.3

A

10.3969/j.issn.1006-0316.2020.01.007

1006－0316 (2020) 01－0041－05

2019－09－03

四川省科技厅应用基础研究项目——基于安全保护功能的高空作业机器人自动控制系统研究（2018JY0132）；成都工业学院引进人才科研启动项目（2017RC009，2017RC007）

文广（1988－），男，湖北荆州人，博士，讲师，主要研究方向为智能机械结构设计与优化、摩擦学。