基于Miura折纸的蜂窝材料共面缓冲性能研究

马瑞君，王玉涛，李 萌，冯 健，蔡建国

1 引言

缓冲着陆装置是航天及航空飞行器中重要的组成部分。在着陆过程中，缓冲器需要吸收和消耗多余动能以保证飞行器的稳定性。传统的缓冲材料多采用正六边形蜂窝，具有轻质、面外刚度较高和压缩行程大等优势，具有良好的缓冲耗能性能。目前针对缓冲着陆过程的研究中，多以材料承受异面压缩的工况为主。然而，在未来的太空探索中，外星球实际的着陆面并非总是平整，着陆过程可能出现颠簸和倾覆。飞行器的缓冲装置有可能面临共面压缩的情况。正六边形蜂窝胞元具有良好的面外刚度，但在承受共面压缩时，会出现胞壁失稳等破坏，平台应力较低，缓冲性能较差。

为提高蜂窝材料的共面缓冲性能，研究人员对六边形胞元进行了改进。Thomas[1]在铝合金蜂窝胞元内增加水平加强筋以提高其刚度，采用试验和仿真的手段研究了这种加强型六边形蜂窝的共面刚度和耗能性能。也有学者采用具有负泊松比的胞元构建新型蜂窝，此类胞元种类繁多，例如内凹六边形胞元、星型胞元、箭头型胞元和手性胞元。在共面受压时，负泊松比胞元的变形机制被激活，材料将向受压区域集中。卢子兴等[2-3]采用数值方法，研究了内凹六边形和手性蜂窝在动态压力下的变形模式和耗能性能，分析了这2种材料的二维负泊松比特性。Qi等[4]对四手性蜂窝进行了面内压缩理论分析、试验研究和数值模拟。加载工况包括准静态和动力压缩，研究给出了此类负泊松比胞元的变形机制、理论模型和平台应力理论公式。卢子兴等[5]采用数值模拟的方法对星型、箭头型和二者的组合型胞元构成的蜂窝进行了面内冲击分析，计算结果指出，组合型胞元有更好的负泊松比特性，体现了最佳的耗能性能和压缩行程。侯秀慧等[6]采用有限元模拟的方法，对多凹角胞元、内凹六边形胞元和正六边形胞元进行了不同速度的面内压缩分析，研究结果指出，低速冲击时，内凹六边形胞元可能出现局部失稳的情况，耗能水平降低，在高速加载时，这种失稳现象消失，凹角胞元和内凹六边形胞元又体现出较高的耗能水平。Hu等[7]对比了内凹六边形蜂窝与传统六边形蜂窝的面内刚度，在局部压力作用下，等壁厚的内凹六边形蜂窝的刚度总是高于传统六边形蜂窝的刚度，但在等相对密度的前提下，内凹六边形蜂窝的泊松比绝对值必须大于特定值ν0时，才有更高的面内刚度，该文献也进一步说明了对于此类胞元，泊松比与面内刚度的关系。

上述所有负泊松比胞元在共面压缩时均体现出二维负泊松比的特性：即材料的xy平面内，当x方向压缩时，y方向收缩，结构的异面方向(z方向)不发生变化。根据文献[2]、[6]的模拟结果，在共面低速(≤7 m/s)压缩过程中，内凹六边形胞元会在低应变时即发生局部失稳，正六边形蜂窝则体现出稳定的压缩变形过程，只有在高速加载时，各层的内凹六边形蜂窝的内凹变形模式才能被激活。简单地引入内凹六边形蜂窝对提高缓冲结构的共面缓冲性能是有限的。为进一步提高蜂窝材料的共面刚度和耗能性能，本文对内凹正六边形胞元进行改进，引入Miura折痕，提出一种新型的蜂窝材料。该材料具有三维负泊松比特性，即在共面压缩时，共面的另一方向及异面方向均体现出材料收缩的特性。

2 几何设计

Miura单元是一种经典的折纸形式，由4个全等的四边形组成，如图1所示。合理的堆叠Miura单元可以形成具有三维负泊松比特性的超材料[8]，如图2所示。当承受挤压时，Miura单元的变形模式被激活，超材料从3个方向向受压处收缩。但是，此类超材料存在面内外刚度较低、拓扑复杂、不宜大规模生产的弊端。

图1 Miura折纸单元Fig.1 Miura pattern

图2 Miura单元组成的超材料[8]Fig.2 Miura folded core metamaterial

相比Miura超材料而言，目前被广泛研究和采用的负泊松比材料为内凹型蜂窝，如内凹六边形蜂窝。此类蜂窝在面内受压时体现出内凹变形机制，如图3所示。

图3 内凹六边形单元变形机制Fig.3 Deformation of auxetic hexagonal cell

为提高内凹六边形蜂窝胞元的共面刚度，避免失稳，同时激发其轴向负泊松比的特性，将2个Miura单元引入内凹六边形胞元中，作为两侧胞壁，形成图4所示的改进型内凹六边形胞元。根据文献[9]，Miura单元的4个几何参数确定，分别为单元基本四边形边长a、b及其夹角γ、单元折叠角θ。对于内凹六边形蜂窝，基本参数包括胞元高度H、胞元边长l、基材密度ρ和内凹角φ。为方便与正六边形蜂窝进行对比，定义φ=120°。将Miura单元引入后，再增加材料高度方向Miura单元的数量参数n。根据图4所示的几何关系，当蜂窝材料的基本参数确定时，Miura单元的参数a、b及折叠角θ可根据式(1)~(3)确定。在不改变内凹角的前提下，蜂窝主要的设计参数为胞元壁厚t及四边形内角γ。正六边形蜂窝和内凹六边形蜂窝相对密度 ρA和 ρB的计算方法如式(4)、(5)所示。 根据式(1)~(3)，考虑内角 γ，对式(5)进行修改，可获得改进型蜂窝的相对密度ρC的计算公式(6)。

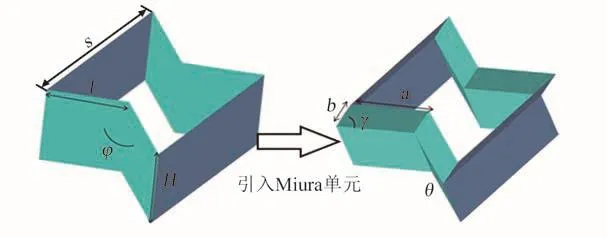
图4 改进型内凹六边形胞元Fig.4 Modified auxetic hexagonal cell

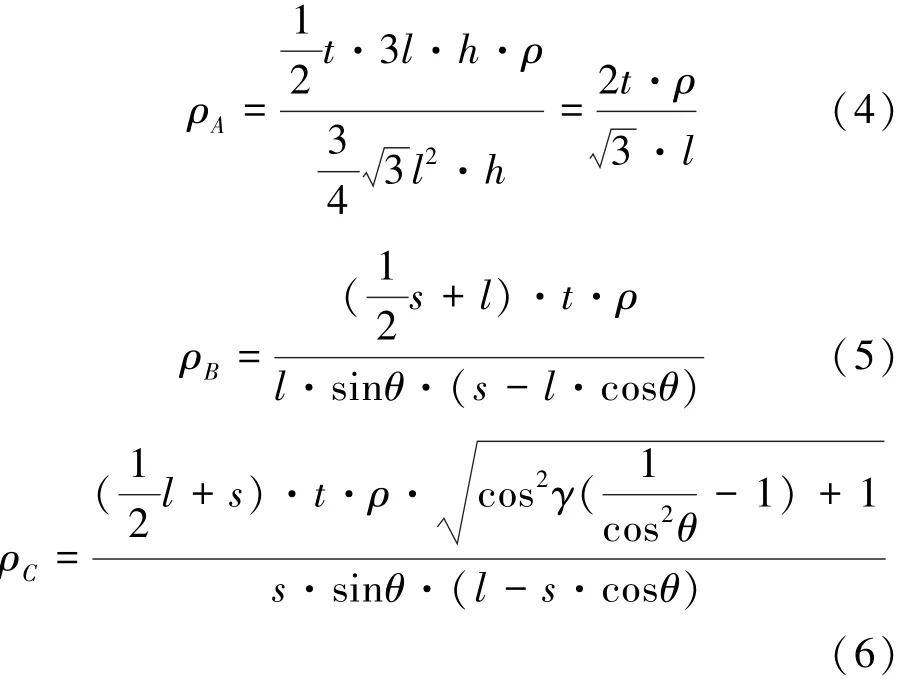
3 准静态压缩性能数值模拟

3.1 有限元模型设计

为验证第2节所提出的改进型内凹六边形蜂窝的共面和异面压缩性能，采用数值模拟的方法建立蜂窝微观有限元模型，进行准静态压缩分析。模型采用ABAQUS有限元软件建立，采用S4R壳单元模拟胞壁。网格尺寸取为0.5 mm×1 mm。共建立3种有限元模型：正六边形胞元蜂窝模型A、内凹六边形胞元蜂窝模型B和改进型内凹六边形胞元蜂窝模型C。材料的共面平面定义为xy平面，异面方向定义为z轴。胞元数量取为7×6，胞元边长取为6 mm，胞元壁厚0.18 mm。根据正六边形内角关系，3种蜂窝的平面尺寸均为x=66 mm，y=62.354 mm，模型高度取为H=40 mm。对于改进型内凹六边形胞元，取单元数量n=2进行研究，选择面内角γ=60°，根据公式(1)~(3)，可确定Miura单元的尺寸a=6 mm，b=12.247 mm，θ=12.247 mm。根据上述参数建立有限元模型如图5所示。蜂窝材料选择3003铝合金，条件屈服强度fy为115 MPa，弹性模量E为69.29 GPa，泊松比μ为0.33，密度ρ为2700 kg/m3。模拟中假定材料为理想弹塑性材料。

为验证3种模型在低速压缩状态下的共面和异面性能，选择准静态加载，下压速度为0.1 m/s，方向取为共面x方向和异面z方向。通过在加载方向定义刚性板实现加载过程。加载中考虑刚性板和蜂窝胞壁、蜂窝胞壁之间的接触摩擦关系。这些接触关系均采用ABAQUS软件中的通用接触关系进行定义。切向摩擦系数取为0.1。2个方向的加载方案如图6所示。

图5 结构有限元模型Fig.5 FE model

图6 边界与荷载条件Fig.6 Boundary and load condition

3.2 共面与异面准静态压缩模拟

3.2.1 共面加载

图7为3种蜂窝材料在共面x方向加载条件下的应力应变曲线(σ-ε曲线)。对于模型A和模型B，其曲线形状比较接近，包含典型的3阶段受力：弹性阶段、平台阶段和压密阶段。其中平台阶段是材料耗能的主要部分，该阶段的平均应力σC(又称平台应力)及压密应变εC是材料缓冲性能的主要指标。模型A与模型B的平台应力σCA=σCB=0.1 Mpa。模型C的曲线则可分为4个阶段：①弹性阶段(ε＜0.01)，该阶段与模型A和B相同，弹性应变较小，其刚度及耗能意义可忽略不计；②聚拢阶段(ε＜0.2)，此时蜂窝材料的折痕产生塑性铰，负泊松比特性被激活，结构开始聚拢变形；③平台阶段(ε＜0.6)，此时材料在承压的yz平面内聚拢为半密实状态以承受x方向压力，是耗能的主要阶段。此时材料的平台应力σCC=2.2 MPa；④密实状态(ε＞0.6)，材料逐渐压缩密实。根据式(4)~(6)，可获得 A、B和 C3种蜂窝的质量 mA=21.93 g，mB=32.19 g 和 mC=37.59 g，可计算模型A、B和C的质量比为1∶1.47∶1.71。根据该计算结果，改进型内凹六边形蜂窝的共面强度比同尺寸的正六边形蜂窝或内凹六边形蜂窝可提高22倍，而质量仅提高70%左右。

图7 3种蜂窝材料共面x方向加载应力应变曲线Fig.7 Load-displacement curves of three honeycomb materials in x direction

3种模型在达到密实应变时(εC=0.6)的变形模式如图8~10所示，对于模型A，在共面x方向压缩条件下，胞壁屈曲明显，塑性区域主要出现在胞壁交接线上。胞壁并未发生大面积的塑性变形即进入了压密状态。从2个视角的模型变形模式可知，结构体现出正泊松比的特征。对于模型B，在共面x方向压缩条件下，并未发生明显的内凹变形模式。胞壁同正六边形蜂窝类似发生屈曲变形，模型在较低的应力水平下发生压溃。对于模型C，在达到密实应变时，材料在y和z方向均出现收缩现象，即出现三维负泊松比特征。为研究这一特征，图11给出了模型C在聚拢阶段(ε=0.2)时的变形云图，并且显示了未变形的状态以方便对比。该时刻的变形模式更进一步说明了，在x方向压缩时，结构体现出明显的三维负泊松比特性。在聚拢状态下，模型C相比A与B，在低应变条件下即达到zy平面内的密实状态，为进一步压缩提供了更大的抗压面积。该变形模式进一步解释了图7所示的模型C的4阶段应力应变曲线。图12为某一胞元在ε=0.2时的塑性应变云图。根据该图可知，塑性区主要出现在折痕处，胞元壁并未出现明显塑性区。此现象说明，Miura变形机制与内凹六边形变形机制相互协调，未发生明显的干涉，因而面内无明显塑性变形。在这种条件下，材料实现了在3个方向的收缩变形，达到聚拢状态。

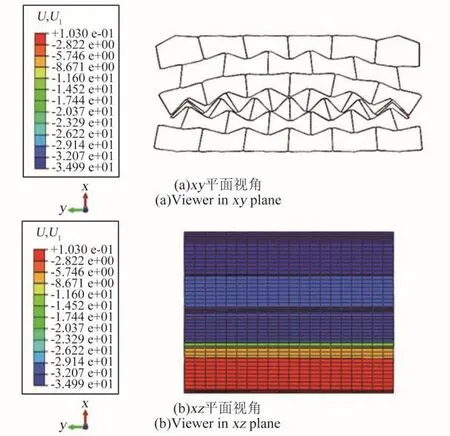
图8 模型A共面x方向压缩时变形云图(mm)(ε=0.6)Fig.8 Deformation nephogram of model A under loading in x direction(mm)(ε=0.6)

3.2.2 异面加载

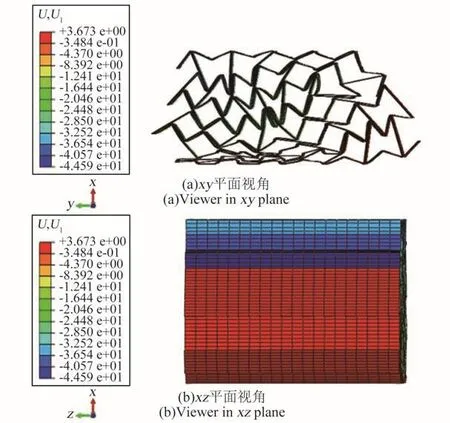
图9 模型B共面x方向压缩时变形云图(mm)(ε=0.6)Fig.9 Deformation nephogram of model B under loading in x direction(mm)(ε=0.6)

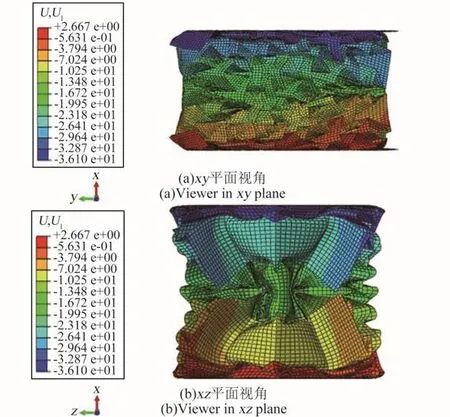
图10 模型C共面x方向压缩时变形云图(mm)(ε=0.6)Fig.10 Deformation nephogram of model C under loading in x direction(mm)(ε=0.6)

图13 为3种蜂窝材料在异面加载条件下的应力应变曲线。模型A和B体现出相似的3阶段变形特征且其平台应力相等：σCA=σCB=3.0 Mpa。模型C的异面耗能性能则明显较低，σCC=0.3 MPa。3种材料的密实应变基本相同，εC=0.7。图14~16为3种材料在压密时刻的变形云图。模型A与B均发生了典型的蜂窝材料逐层压溃变形模式，体现了良好的耗能性能。模型C的变形则主要依赖Miura机制进行折叠。该机制在异面加载时易于发生轴向屈曲，导致耗能水平下降。图17为应变ε=0.1、0.3、0.5和0.7时模型C的变形云图(xy平面视角)。与原始模型尺寸相比，结构体现出明显的双向负泊松比特性，即结构存在三维负泊松比。

图11 模型C共面x方向压缩时变形云图(mm)(ε=0.2)Fig.11 Deformation nephogram of model C under loading in x direction(mm)(ε=0.2)

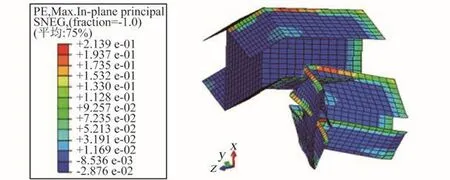
图12 胞元塑性应变云图Fig.12 Plasticity nephogram of cell

图13 3种蜂窝材料异面加载荷载位移曲线Fig.13 Load-displacement curves of three honeycomb materials under out-of-plane loading

图14 模型A异面z方向压缩时变形云图(mm)(ε=0.7)Fig.14 Deformation nephogram of model A under loading in z direction(mm)(ε=0.7)

图15 模型B异面z方向压缩时变形云图(mm)(ε=0.7)Fig.15 Deformation nephogram of model B under loading in z direction(mm)(ε=0.7)

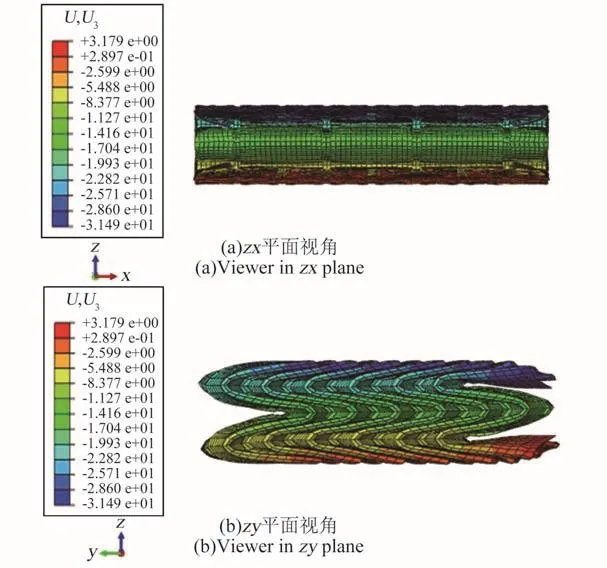
图16 模型C异面z方向压缩时变形云图(mm)(ε=0.7)Fig.16 Deformation nephogram of model C under loading in z direction(mm)(ε=0.7)

图17 模型C在各应变时刻的变形云图(mm)Fig.17 The deformation nephogram of model C under different strains(mm)

4 折纸型二级缓冲结构设计

采用蜂窝材料设计的缓冲结构，由于加工原因，多设计成多级蜂窝，如图18所示。文献[10]提出，通过改变蜂窝的型号尺寸，构建出由具有不同刚度的蜂窝组成的串联式缓冲结构，更适用于多种缓冲着陆工况。根据第3节的模拟结果可知，改进型内凹六边形蜂窝具有良好的共面压缩性能，而且所提蜂窝的异面刚度较低，耗能较少。基于上述特征，可利用所提蜂窝材料和无折痕的内凹六边形蜂窝材料进行串联组合，设计满足多种着陆工况的折纸型二级缓冲结构，如图19所示。此类结构在正常的着陆缓冲过程中，一级折痕蜂窝首先被压缩实现缓冲耗能。在严苛着陆过程中，二级无折痕蜂窝可提供更高的缓冲耗能。同时，当着陆遭遇水平压缩工况时，一级折痕蜂窝则提供较高的侧向刚度，进行平面内缓冲耗能。同时，相比于传统的串联缓冲结构，此类结构不需要通过改变蜂窝胞元尺寸以实现强度的梯度变化。该设计可省略隔板以减少缓冲结构重量。

图18 二级缓冲结构Fig.18 Two-stage buffer structure

图19 折纸型二级缓冲结构Fig.19 Miura two-stage buffer structure

为验证上述设计的可行性，建立缓冲结构的有限元模型并进行共面与异面的准静态压缩分析。其中，改进型内凹六边形蜂窝的有限元模型的设计参数同3.1节。单层无折痕蜂窝的高度为20 mm，其余参数与3.1节相同。采用共用节点的方法将3部分蜂窝进行连接。结构总高度80 mm。在准静态压缩条件下，结构的应力应变曲线如图20、21所示。由图可知，在共面加载条件下，折纸型二级缓冲结构体现出较好的共面耗能性能，平台应力达到0.6~0.8 MPa。在异面加载条件下，折纸型二级缓冲结构体现出明显的2阶段缓冲性能。相比于传统的二级缓冲蜂窝，其峰值应力较低，更容易实现软着陆。

图20 折纸型二级缓冲结构共面加载应力应变曲线Fig.20 Stress-strain curve of Miura series buffer structure under in-plane load

图21 折纸型二级缓冲结构异面加载应力应变曲线Fig.21 Stress-strain curve of Miura series buffer structure under out-of-plane load

5 结论

1)改进型内凹六边形蜂窝在共面加载时，体现出优良的面内刚度和耗能性能，其机制在于材料存在独特的聚拢阶段，具有三维负泊松比特性；

2)改进型内凹六边形蜂窝在异面加载时，体现出较低的面外刚度和耗能水平，其原因在于结构会在发生胞壁压溃前先引发Miura机制导致失稳；

3)二级缓冲结构满足飞行器在正常和特殊着陆工况下的缓冲性能要求。