滚卷式太阳毯结构张力保持系统与动力特性研究

沈银祥，项 平∗，吴明儿，商红军，关富玲

1 引言

空间太阳电池阵是航天器的核心供电设备[1]。随着航天器功率需求的增大，对低成本、高功率的大型空间太阳电池阵的需求随之不断增大。滚卷式太阳毯是美国可展开空间系统公司首先提出并研制成功的一种新型柔性太阳电池阵[2]，采用滚卷式展开方式，即太阳毯卷绕收拢滚动展开。太阳毯采用质量较小的薄膜基板，可以获得较大的质量比功率；结构上的独立性使得与航天器本体有较好的适应性；卷式机构能实现多次展开与任意的半展开状态，在空间具有较好的机动性，而其他型式的太阳电池阵较难完成这样的任务[3]。国外研究人员对滚卷式太阳毯进行了深入的研究，如国际空间站滚卷式太阳电池阵已经完成航天飞行试验[3-4]。国内研究人员对柔性太阳电池阵已有研究，如郭其威等[5]研究中国空间站太阳电池阵伸展机构临界屈曲荷载和整翼基频。目前国内对大型滚卷式太阳毯的研究尚处在起步阶段，有必要对其进行深入的研究。

航天器柔性附件的模态特性是姿态控制系统设计的重要指标[6]。为保证滚卷式太阳毯展开后的模态特性和平面形状，必须对其施加足够张力且在太空环境下保持不变。我国空间站柔性太阳电池阵采用张紧绳和桁架伸展机构作为张力保持系统[7]。本文设计一种采用恒力弹簧的滚卷式太阳毯张力保持系统来保证毯面的张力恒定，利用理论推导和有限元软件分析毯面的动力性能，并通过制作原理样机测试太阳毯模型的自振频率和平面度。

2 滚卷式太阳毯结构张力保持系统

2.1 张力保持系统组成及设计

太阳毯主要包括伸展杆、外端卷轴、根部横梁、毯面和张拉系统。毯面分3层，从底层到顶层依次是纤维网面、膜面和电子元器件，如图1所示。张拉系统主要包括恒力弹簧、传力梁和网面。恒力弹簧通过传力梁将恒定集中力均匀地传给网面，再由网面将张力均匀地传给膜面。在太阳毯毯面发生变形时，恒力弹簧张力保持不变，从而保证毯面始终保持张紧状态且张力恒定。

恒力弹簧采用0.1~0.2 mm的钢带或合金板材卷制而成，如图2所示，它的特点是成形后弹簧任一圈的自然曲率相等[8]。为保证恒力弹簧使用性能，需将其套在滚筒上，滚筒材料可选用硅胶、聚氨酯等。

图1 太阳毯毯面张力保持系统Fig.1 Tension-keeping system of roll-out solar array

图2 恒力弹簧与滚筒Fig.2 Constant force spring and roller

根据材料力学理论[9]，可推出恒力弹簧尺寸设计公式，如式(1)所示：

式中，P为张拉力，E为材料弹性模量，b为钢带宽度，t为钢带厚度，R为弹簧钢带曲率半径，v为材料泊松比。

由于恒力弹簧材料性能、制作工艺误差以及拉伸过程中外圈半径逐渐减小等原因，通过拉伸试验获取恒力弹簧荷载-变形关系。图3为定制的恒力弹簧(1号~5号)的荷载-变形关系曲线。恒力弹簧2号、4号和5号张拉力较恒定；恒力弹簧1号和3号张拉力在拉伸长度小于10 cm时基本保持不变，拉伸长度超过10 cm后，张拉力随拉伸长度增加而减小。根据恒力弹簧荷载-变形关系，挑选出在张拉过程中张拉力保持恒定的恒力弹簧(2、4、5号弹簧)应用于太阳毯毯面张力保持系统中。

2.2 太阳毯毯面张拉数值分析

图3 恒力弹簧荷载-变形曲线Fig.3 Load-deformation curve of constant force springs

采用有限元软件ABAQUS数值模拟恒力弹簧张拉下的网面和膜面的应力状态。网面、膜面和传力梁均选用S4R类型壳单元，膜面和传力梁通过绑定约束与网面建立接触关系，外端卷轴和恒力弹簧分别简化为简支边界和集中荷载，有限元模型如图4所示。各部分材料特性如表1所示。考虑毯面的非结构附加质量(如粘结剂等)50 g/m2，恒力弹簧合力F取170.5 N，分11个集中力均匀施加到传力梁上，数值分析结果如图5所示。

图4 有限元模型Fig.4 Finite element model

表1 材料特性Table 1 Material properties

由Mises等效应力SMises应力云图可看出，网面和膜面中部大范围应力均匀，只在左右两端小范围出现较大和较小应力。由第二主应力S2应力云图可看出，网面中间很大区域出现负应力，而整个膜面均未出现负应力，根据判别褶皱的主应力准则[10]，可认为网面发生了褶皱而膜面未发生褶皱。设SMises均匀区域中心处的SMises值为S，定义SMises值为(1±10%)×S以内的区域为有效区域，膜面有效区域面积与膜面面积之比为膜面有效区域率η。由图6可看出在不同恒力弹簧合力F作用下，膜面有效区域率η均可达到约97%，表明膜面应力均匀性较好。

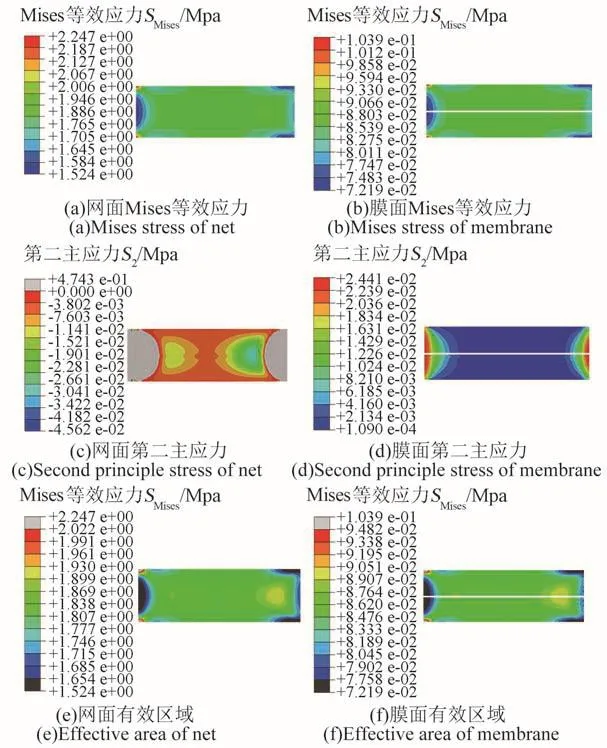
图5 张力保持系统的数值模拟Fig.5 Numerical simulation of tension-keeping system

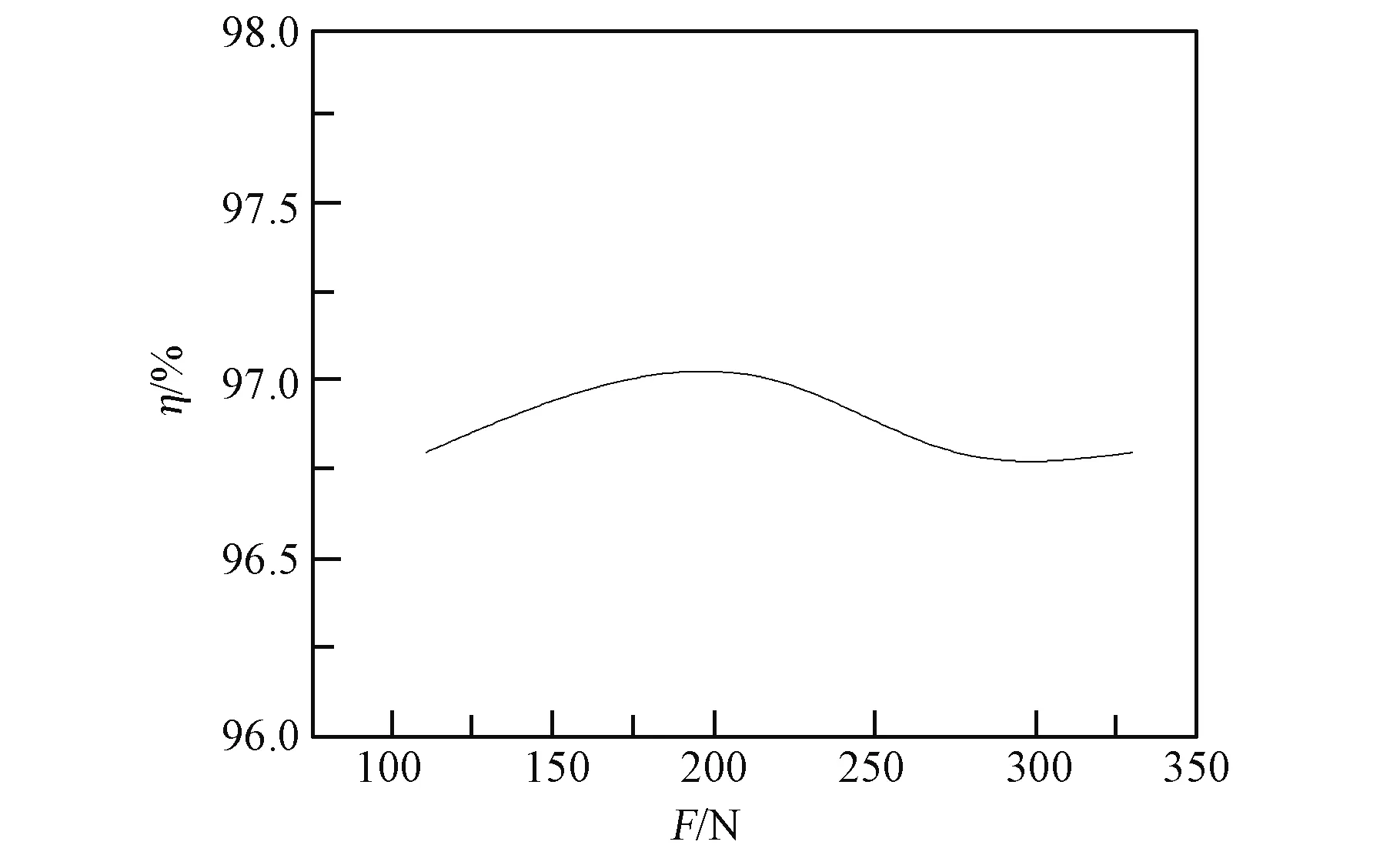
图6 恒力弹簧合力与膜面有效区域率关系Fig.6 Relationship between load and membrane effective area rate

3 滚卷式太阳毯毯面动力学分析

3.1 毯面基频理论计算模型

毯面可简化为张拉膜结构，张拉着的薄膜是张拉着的弦的二维相似物[11]。一对边张拉，一对边自由的矩形薄膜(图7)的横向振动与弦的横向振动类似。薄膜面密度为 ρ，线张力为σ，长度为l。

理论分析前做如下基本假定：

1)薄膜只发生横向振动，即各点振动方向垂直于平衡位置；

2)薄膜只发生微小振动，即振动幅度与薄膜切线倾角都很小；

3)薄膜的张力总是沿着切线方向；

4)忽略重力和阻尼影响。

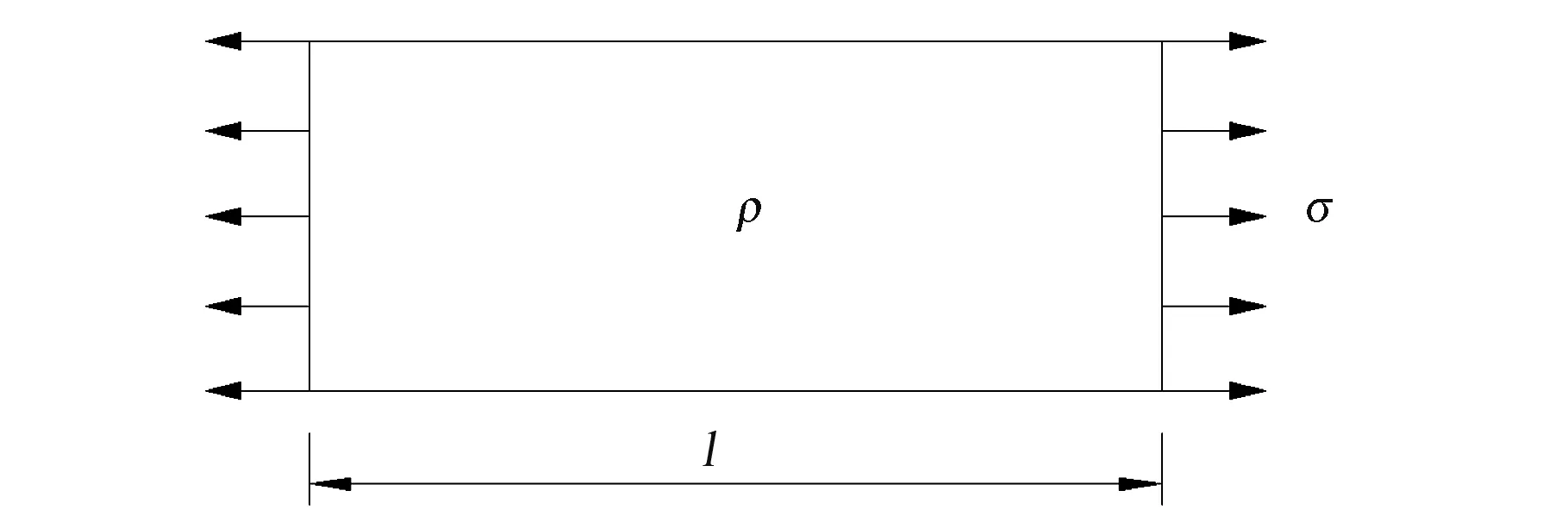
图7 一对边张拉一对边自由的矩形薄膜Fig.7 Rectangular membrane with two opposite sides tensioned and other two sides free

取单位宽度张拉薄膜作为研究对象，如图8所示。设薄膜在未受扰动时，平衡位置是x轴，两端分别固定在x=0和x=l处，则t时刻薄膜形状曲线为y=y(x，t)。任取一小段薄膜L1L2，忽略重力和阻尼影响，根据结构动力学理论[12]，对薄膜L1L2的振动采用拉格朗日运动方程描述，如式(2)所示：

式中，m为薄膜的质量，y¨为薄膜在y轴方向的加速度，fy为薄膜在y轴方向外力的合力。

图8 单位宽度薄膜横向振动Fig.8 Transverse vibration of unit width membrane

因薄膜只发生微小横向振动，进而可得式(3)：

将式(3)代入(2)得式(4)：

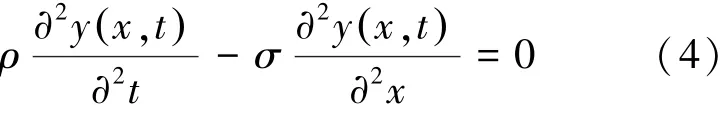
设 y(x，t)=X(x)T(t)，将边界条件 y(0，t)=0、y(l，t)=0代入式(4)可求得薄膜横向振动频率计算公式(5)：

式中，n为自然数，即振型阶数。

薄膜横向振动基频如式(6)所示：

3.2 毯面基频有限元与理论计算对比

采用图4的有限元模型计算毯面频率。电子元器件长度和宽度均与膜面相同，厚度为0.15 mm，密度为250 g/m2，弹性模量为8 GPa，泊松比为0.3，在整个膜面上均匀分布，选用S4R类型单元，通过绑定约束与膜面建立接触关系，电子元器件不参与刚度贡献，但增加结构质量，降低振动频率。同时考虑毯面的非结构附加质量分别为50 g/m2、100 g/m2和150 g/m23种情况。 为了调节基频一致，对应的总荷载分别取170.5 N、194.8 N和219.0 N。毯面基频有限元分析结果与根据式(6)得到的理论计算结果对比如表2所示。不同附加质量及对应的荷载作用下，毯面基频的有限元计算值为0.153 Hz，由式(6)计算的理论值为0.150 Hz，误差1.96%，证明了有限元模型的正确、可行。

表2 毯面基频有限元与理论计算结果Table 2 Results of fundamental frequency of roll-out solar array by finite element and theoretical calculation

4 原理模型试验

4.1 原理模型设计

为验证滚卷式太阳毯张力保持系统的有效性及毯面基频理论计算模型的正确性，设计原理样机并进行相关试验研究。太阳毯原理试验样机如图9所示。空间展开机构在地面与外太空的区别之一在于地面存在重力影响。针对空间零重力环境设计的太阳毯，无法克服自身重力，设计卸载装置对各展开部件进行重力卸载，最大限度地降低地面重力对机构地面试验的影响[13]。本文采用悬吊法[14]进行重力卸载。将外框架固定在支撑框架上，利用吊绳将网面悬挂在外框架上，吊绳可以沿着竖向对网面施加拉力。非结构附加质量采用硅胶板粘贴在网面背面。

图9 太阳毯原理试验样机Fig.9 Principle prototype of roll-out solar array

4.2 自振频率测试

采用非接触式的IL-300型激光位移传感器测量毯面的平面外振动位移响应，数据采集设备采用美国NI公司生产的CompactDAQ系统。测点布置如图10所示，激振方式为对毯面中心点(C1位置)施加垂直于毯面的冲击荷载。对不同非结构附加质量的太阳毯的振动试验数据进行处理，得到其位移-时间曲线和振幅-频率曲线，如图11所示。

图11纵坐标中s表示测点处平面外位移，A表示傅里叶变换后得到的频响函数幅值。薄膜在空气中振动时，空气附加质量对试验结果影响显著，频率分析需考虑空气附加质量。薄膜振动的空气附加质量分布相当于振型各区域上均匀分布0.65倍该振型区域特征长度的空气，见式(7)：

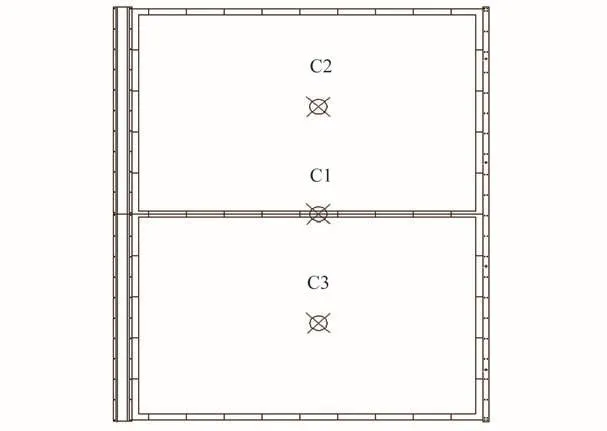
图10 测点布置Fig.10 Arrangement of measuring points

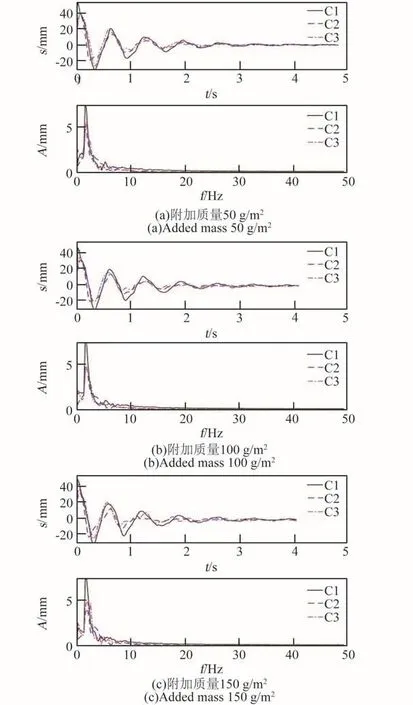
图11 不同附加质量的振动试验结果Fig.11 Results of vibration test with different additional masses

式中，ma为空气附加质量，ρ为空气密度，l为振型区域特征长度，取该区域内切圆直径[15]。试验测得的毯面振动主要为1阶振型，由式(7)可计算得毯面1阶振型的空气附加质量为0.977 kg/m2。表3给出了不同附加质量试验模型振动基频的理论值、有限元计算值和试验值。此处的基频理论值与表2的足尺太阳毯的基频理论值并不一致，这是因为在保证试验模型毯面线荷载与足尺太阳毯毯面线荷载一致的前提下，试验模型毯面尺寸较足尺太阳毯小且考虑了空气附加质量。

表3 毯面振动基频结果Table 3 Fundamental frequency of roll-out solar array

由表3的结果可知，试验模型振动基频的理论值与试验值最大误差为4.6%，有限元与试验值最大误差为3.4%，验证了滚卷式太阳毯张力保持系统的有效性及毯面基频理论计算模型的正确性。

4.3 平面度测试

滚卷式太阳毯展开状态下毯面的平面度是其所承载的电子元器件正常工作的重要保证。太阳毯是柔性薄膜结构，采用非接触测量法进行毯面平面度测试[16]，测量设备采用DIC数字图像测量系统，图像处理采用GOM Correlate软件。Kapton薄膜为黄色半透明薄膜，需在膜面上粘贴靶点作为目标点。试验装置及靶点布置如图12所示，试验模型中网面厚0.37 mm，膜面厚0.05 mm。根据采集到的靶点坐标算得毯面平面度RMS误差为2.62 mm。利用MATLAB软件对毯面进行曲面拟合，采用pointCloud和pcshow函数求得毯面各靶点处法线，如图13所示。靶点处法线与设计阵面法线夹角最大为 6.07°，最小为 2.65°，RMS值为3.94°，结果表明毯面未能完全张紧，局部出现褶皱，应提高加工制作工艺改善毯面平面度。

5 结论

1)通过原理模型验证了设计的滚卷式太阳毯结构张力保持系统的可行性。

2)通过太阳毯有限元模型张拉数值分析表明膜面未出现褶皱且膜面应力均匀性良好。

图12 DIC试验装置和靶点布置Fig.12 DIC testing device and target spots on membrane

图13 毯面靶点拟合面及其靶点处法线(mm)Fig.13 Target fitting surface and normal line at target spots(mm)

3)基于建立的滚卷式太阳毯毯面基频理论计算公式，与有限元及试验测试的结果对比，三者基频结果吻合较好，验证了滚卷式太阳毯张力保持系统的有效性及毯面基频理论计算模型的正确性。

4)通过对滚卷式太阳毯原理模型采用非接触测量法进行平面度测试，表明毯面平面度尚可，但仍需通过改进加工制作工艺以改善毯面平面度。