基于SST k-ω的超声速气膜冷却湍流模型温度修正
李子亮,于 洋,刘登丰
1 引言
超燃冲压发动机和大推力液体火箭发动机的高热负荷组件的热防护面临严峻考验。长期以来,气膜冷却的应用主要集中在以燃气涡轮冷却为代表的亚声速范围。近年来,随着先进发动机的发展,超声速气膜冷却以其更高的冷却效率逐渐应用于超燃冲压发动机燃烧室和大推力火箭发动机喷管的热防护。与常规亚声速气膜冷却相比,超声速气膜冷却压缩性作用显著,气体动量与能量紧密耦合,机理十分复杂。目前超声速气膜冷却可压缩效应尚未完全清楚,温度梯度和速度梯度耦合作用下的剪切层混合传热规律有待进一步阐明。
随着计算流体力学(Computational Fluid Dynamics,CFD)的发展,CFD模拟成为研究超声速气膜冷却的重要手段。在超声速气膜冷却数值模拟中,从不可压缩流动发展而来的湍流模型是最具不确定性因素的,在预测高速流动时可压缩性不可忽略,需要对模型进行可压缩修正。多年以来,以Sarkar[1-2]和Henze[3]为代表的研究者以标准k-ε模型为基础进行了大量修正工作。现有湍流模型已包含自由剪切层可压缩耗散的修正项,但并未将温度变化对剪切层增长速率的影响考虑在内,导致超声速气膜冷却可压缩流动传热预测结果不理想[4-6]。
超音速气膜冷却的流动包含自由剪切流与附体流,而目前工程中广泛应用的标准k-ε模型[7]只适用于计算高雷诺数湍流。Menter[8]提出的SST k-ω模型结合了k-ε模型与k-ω模型[9]的特点,对于近壁面低雷诺数流动采用标准k-ω模型计算,而在远壁面完全湍流区切换为k-ε模型,因此该模型可用于受限空间超声速气膜冷却的数值模拟。然而,现有SST k-ω湍流模型继承了k-ε模型的缺陷,在用于预测超声速气膜冷却之前,需要进行修正。
本文拟在现有SST k-ω湍流模型基础上,充分考虑剪切层温度变化对冷却气体与主流混合传热的影响,对其进行温度修正,并通过实验数据对修正后的模型进行验证。
2 模型建立与修正
2.1 控制方程
超音速气膜冷却流动过程满足粘性可压缩N-S方程,流体传输过程遵循质量守恒、动量守恒和能量守恒,其控制方程如式(1)~(3)所示。
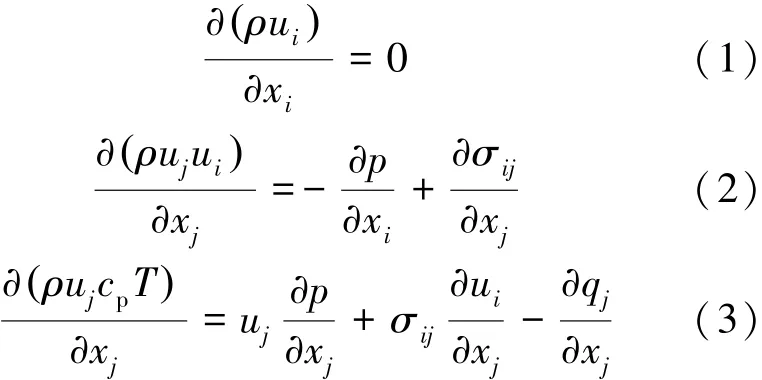
对于超音速气体,应满足如式(4)所示理想气体状态方程。

式(1)~式(4)中,u为速度,q为热流量,σij为粘性张量,cp为比热容,ρ为密度,T为温度,p为压力,R为气体常数。
2.2 SST k-ω湍流模型温度修正
SST k-ω双方程湍流模型中湍动能k与比耗散率ω的输运方程如式(5)~式(10)所示。

SST k-ω模型湍流粘度表达式如式(11)~(13)所示。

式(5)~式(13)中,τij为雷诺应力张量,Ω为涡度张量,μ为层流粘度,μt为湍流粘度,y为到壁面的距离,模型常数 a1=0.31,β∗=0.09,κ=0.41,σk1=0.85, σω1=0.5, σk2=1.0, σω2=0.856。
由于超声速气膜冷却剪切层存在较大温度梯度,本文模型修正的目的是将温度变化对剪切层发展的影响加入到SST k-ω模型中,方法如下。
通过总温梯度和湍流长度尺度定义修正变量Tg,其表达式为式(14)。
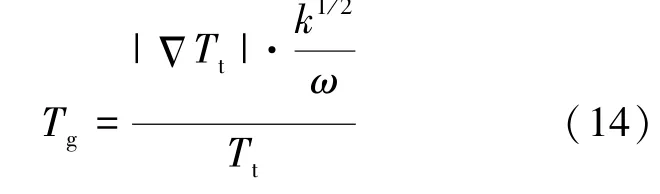
式中,Tt为气体总温,ΔTt为总温梯度, k1/2/ω为湍流长度尺度。
修正函数CT的表达式为式(15)。
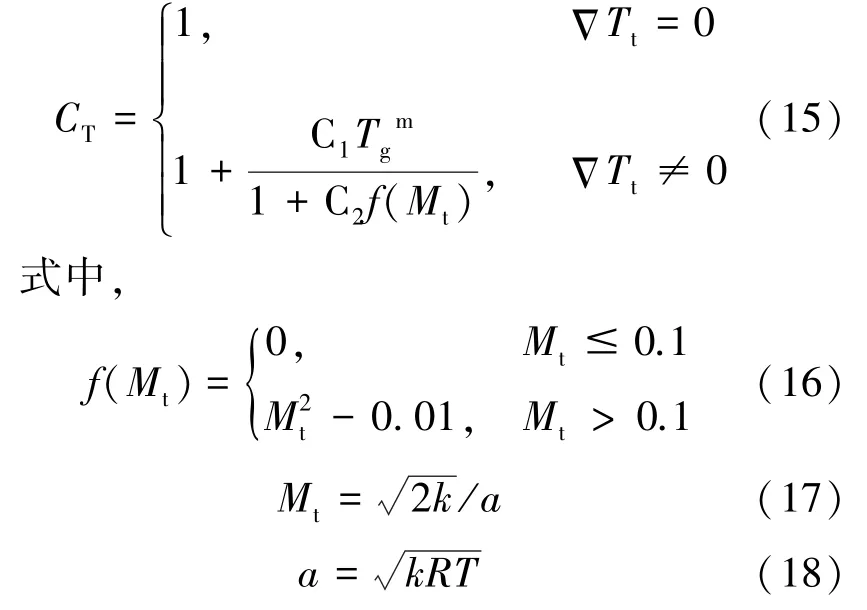
式(15)~式(18)中,C1、C2和m为修正函数CT中的常数,Mt为湍流马赫数,Mt≤0.1时,f(Mt)=0,即不进行可压缩修正,a为当地声速。因此,本模型修正是在可压缩SST k-ω模型基础上进行温度修正。
温度修正后的SST k-ω湍流粘度为式(19)。
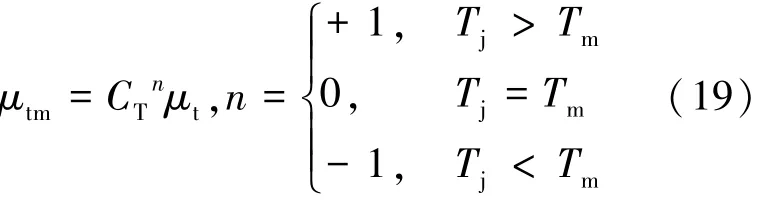
式中,Tj为冷却气体温度,Tm为主流温度,在超声速气膜冷却中,当冷却气体入射温度小于主流温度时,取n=-1。该修正模型适用于计算剪切层总温梯度较大的湍流混合耗散过程。
3 模型验证
3.1 非等温可压缩湍流混合
采用Sumi[5]的超声速低温射流与高温气体自由剪切混合的实验数据对模型的修正效果进行初步验证。建立与实验相同的二维计算域,并采用相同的边界条件,如表1和图1所示。将计算域划分为173 000个网格,壁面绝热无滑移,气体为可压缩氧气,采用密度基求解器进行计算。
采用修正前后的SST k-ω湍流模型计算温度为Tj=190 K超音速气体射入1002 K高温气体环境中时得到的湍动能分布如图2所示。由图可知,修正后的模型与修正前相比,剪切层垂直于射流方向,湍动能增长受到抑制,沿射流方向湍动能衰减变慢,这表明温度修正后的SST k-ω湍流模型有效抑制了大温度梯度下剪切层的增长速率,修正效果显著。

表1 非等温可压缩自由剪切流边界条件Table 1 The boundary condition of the non-thermal free shear flow
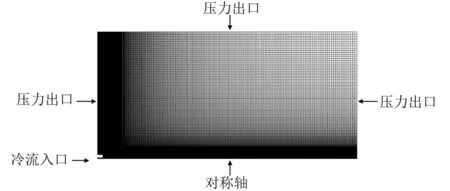
图1 非等温可压缩湍流混合计算域网格划分Fig.1 Mesh generation in computational domain for non-isothermal compressible turbulent mixing
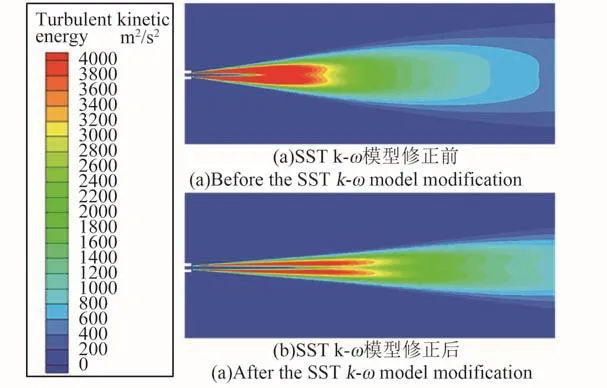
图2 SST k-ω湍流模型修正前后计算得到的湍动能分布(T j=190 K,T a=1002 K)Fig.2 The calculated turbulent kinetic energy distribution before and after the SST k-ωmodel modification(T j=190 K,T a=1002 K)
图3 为不同湍流模型计算得到的非等温可压缩湍流射流轴向速度分布,从图中可知温度与可压缩修正后的SST k-ω湍流模型计算结果与相同条件下的实验结果吻合,而可压缩修正的k-ω模型与SST k-ω模型的计算结果与实验值相差较大,这进一步说明了温度和可压缩修正的SST k-ω湍流模型对于大温度梯度自由剪切流预测的准确性。在此基础上,将修正模型用于预测同时含自由剪切流和附体流的超音速气膜冷却行为的准确性进行验证。

图3 非等温可压缩湍流射流轴向速度分布(T j=190 K,T a=1002 K)Fig.3 Axial velocity distribution of the non-isothermal compressible turbulent(T j=190 K,T a=1002 K)
3.2 超声速气膜冷却传热
采用Holden[10]的绝热平板超声速气膜冷却实验数据对修正模型的计算结果进行验证。并采用与实验相同几何尺寸与边界条件进行建模,相关参数如表2所示。

表2 平板气膜冷却计算域尺寸参数Table 2 The calculating domain size of flat plate film cooling /m
图4为平板超声速气膜冷却计算域,将计算域划分为256 089个网格,对壁面和冷却气体入口附近网格做加密处理,第一层网格节点距壁面0.005 mm。
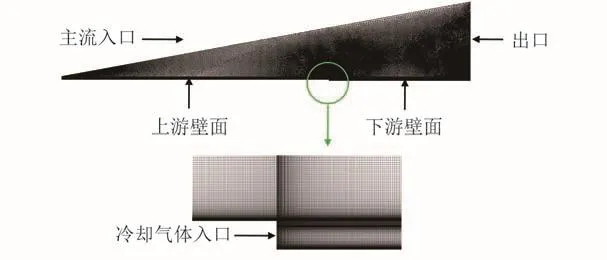
图4 平板超声速气膜冷却计算域网格划分Fig.4 Mesh generation in computational domain for supersonic film cooling of flat pate
超声速气膜冷却主流为空气,冷流为氦气,氦气通过小喷管加速后在凸台下游与空气进行掺混,将小喷管出口参数作为冷却气体在流场中的入射边界参数。具体的实验方案如表3所示。方案1为无气膜冷却下的超声速空气主流在无凸台平板上流动,方案2为无气膜冷却的超声速空气主流在下游壁面流动,方案3为气膜冷却下超声速氦气与空气主流在下游混合流动。壁面条件设置为光滑绝热无滑移,壁面温度为294.26 K,选择密度基求解器进行计算求解。
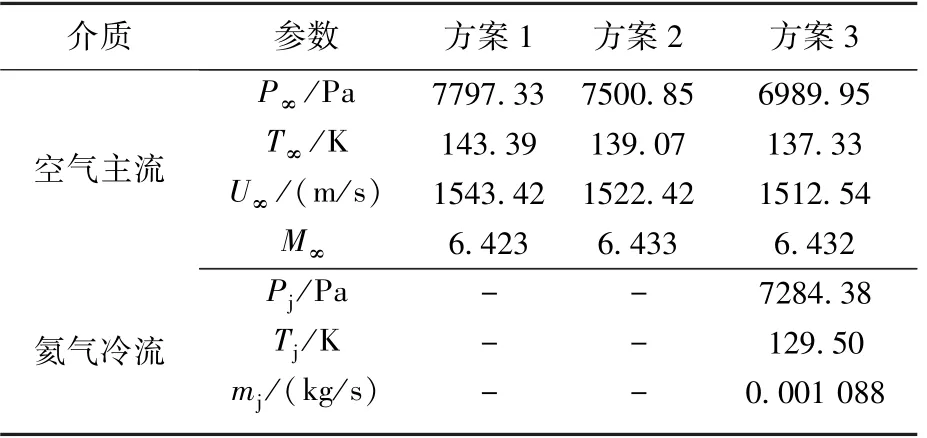
表3 超声速气膜冷却实验方案与入射参数Table 3 Experimental scheme and injection parameters of supersonic film cooling
图5为空气主流作用下平板壁面热流轴向分布曲线,图6为空气主流作用下凸台下游平板壁面热流轴向分布曲线。从图中可知,温度和可压缩修正的SST k-ω模型计算得到的无凸台平板x>0 m区域(图5)和凸台下游(图6)的壁面热流与实验值吻合最好,而采用可压缩修正的k-ω和SST k-ω模型的计算值均较实验值偏高。这是因为温度修正的SST k-ω模型是在可压缩修正的基础上考虑了温度变化对剪切混合的影响,进行了温度修正,弥补了现有模型过高或过低预测剪切层增长速率的缺陷,模型更加完善,从而使计算结果与实际更为接近。

图5 空气主流作用下平板壁面热流分布Fig.5 Heat flow distribution on flat plate wall under the action of air mainstream

图6 空气主流作用下凸台下游平板壁面热流分布Fig.6 Heat flow distribution on upstream flat plate wall of the boss under the action of air mainstream
图7 为平板凸台下游超声速冷却氦气与空气相互作用下壁面热流的轴向分布曲线。从图中可知,在初始混合区(x<0.1 m)计算结果与实验结果存在加大差距,这是由于本文计算中将冷却气体入射边界y方向设置为均一参数,使初始区壁面边界层气体温度过低,热流偏高。比较图中3个湍流修正模型在充分混合区的结果可知,温度和可压缩修正的SST k-ω模型与实验结果最为接近。这是因为经过温度修正后的模型可以更加准确预测冷却气体与主流剪切层的混合发展速率;此外,比较与温度和可压缩修正的SST k-ω模型的计算结果可知,在前半段与温度修正模型计算结果接近,而在充分发展区二者计算结果差距变大,可压缩修正的k-ω模型对于湍流充分发展区的预测表现出一定的局限性。由此可知,在可压缩修正的SST k-ω模型基础上构建的温度修正模型适用于预测超声速气膜冷却湍流剪切层的发展变化,确保了冷却气体与高温主流剪切混合传热计算结果的准确性。
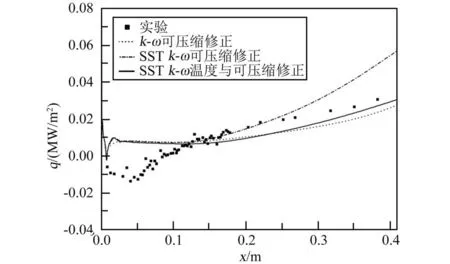
图7 气膜冷却作用下凸台下游平板壁面热流分布Fig.7 Heat flow distribution on upstream flat plate wall of the boss under air film cooling
4 结论
1)温度变化对超声速气膜冷却剪切层湍流混合耗散影响显著,基于总温梯度变化的SST k-ω修正模型弥补了现有湍流模型的理论缺陷,大幅度提高了非等温超声速自由剪切流的计算精度。
2)温度修正的SST k-ω模型对绝热平板超声速气膜冷却的计算结果与实验结果吻合,对于剪切层总温大梯度变化的超声速气膜冷却数值模拟,该模型与现有可压缩修正模型相比具有显著优越性。
3)温度修正的SST k-ω模型有待通过更多的实验数据进一步验证和完善,进而指导液体火箭发动机喷管超声速气膜冷却方案的设计。

