典型机械加工表面形貌统计参数分析

方 兵， 叶峻锋， 孟素各， 顾天奇

(1. 福建农林大学机电工程学院， 福建 福州 350002； 2. 福州大学机械工程及自动化学院， 福建 福州 350108)

0 引言

机械加工表面微观的不平整性导致零部件连接部位刚度、 电阻和接触热阻等物理特性发生非线性的变化. 在采用计算机辅助设计(CAE)开发产品时， 这种变化将影响设计的准确性. 因此， 如何建立零件连接部位(即结合部)的分析模型是解决上述问题的关键. 基于统计表面形貌统计参数研究粗糙表面接触特性是常见的方法[1-3]. 采用统计模型的首要任务是确定“凸峰”的几何属性， 包括位置、 高度(或高度分布)、 曲率半径以及分布密度等信息. 目前， 解决这一问题的基本思路是： 在一定范围内寻找局部最高点， 并以该点附近的点拟合得到一个“凸峰”， 再计算其曲率半径和高度等信息. 根据搜索范围的不同有3点峰准则[4-5]、 5点峰准则[6]、 7点峰准则[7]等. 上述方法很好地解决了“凸峰”确定问题， 但往往会导致表面轮廓线不连续； 其次， 这些方法一般采用分型函数(WM函数)生成表面形貌数据， 从而导致该方法生成的数据和实际有差别. 因此， 本研究基于样条曲线拟合理论和凸峰独立的原则， 提出一种新的凸峰定义方法. 在此基础上， 测取不同机械加工表面的形貌数据， 分析粗糙表面形貌的统计参数， 并对比分析了不同加工方法、 不同粗糙度值的表面形貌数据.

1 表面形貌统计参数分析

1.1 凸峰的定义

机械加工表面形貌可以看作是一个各态历经的平稳随机过程， 不能用确切的函数表达式来描述. 为能够分析其统计特性， 对表面形貌数据采样， 得到表面离散点数据， 并采用三次样条曲线拟合表面形貌数据[8]. 对某一表面轮廓以步长Δh等间隔采样， 得到离散点序列(xi,yi)(i=0, 1, …,k)，xi为取样长度，yi为表面轮廓高度. 在子区间 [xi,xi+1] (i=0, 1, …,k-1)内， 建立插值函数

fi(x)=aix3+bix2+cix+di

(1)

其中：ai,bi,ci,di是待定系数. 通过给定子区间的连续条件(即一阶导数和两阶导数连续)和2个附加的边界条件(给定两端一阶导数值)， 即可求解出所有待定的系数， 确定唯一的三次样条曲线[8].

凸峰在微观表面形貌中意味要高于周围的点， 且在载荷的作用下， 不与周边的凸峰发生干涉. 直接利用三次样条拟合得到的曲线， 往往会出现“峰上峰”的现象， 这不符合凸峰的定义.

图1 表面微观形貌示意图Fig.1 Schematic of microscopic surface morphology

为避免出现凸峰重叠现象， 规定： 若拟合曲线中两凸峰的距离小于3×Δh时， 将由一个新的凸峰代替现有的两个凸峰. 如图1所示， 点i至点i+4形成的凸峰互相干涉. 此时， 保留两个端点(即Pi和点Pi+4)， 定义新的点PN替代点Pi+1、Pi2和Pi+3， 点PN为两峰值点的中心， 需满足关系

(2)

式中：Ps1和Ps2分别为两个凸峰的坐标.

得到PN坐标后， 再次利用三次样条曲线拟合， 得到新的拟合曲线. 重复检测凸峰之间的距离， 并按公式(2)得到新的拟合点， 便可解决凸峰重叠的现象.

1.2 凸峰高度分布函数

实际上两个表面相互接触时， 往往不是全部表面接触， 而是一些“凸峰”接触， 或一个表面的“凸峰”伸入另一表面的“凹谷”中， 形成交错. 因此， 需要找到拟合曲线的局部最大值， 并分析其高度分布规律. 拟合后曲线的局部最高点对应表面的“凸峰”， 局部最低点对应表面的“凹谷”.

在子区间[xi,xi+1] (i=0, 1, …,k-1) 内有插值函数fi(x), 求解该函数的一阶导数f′i(x)和二阶导数f″i(x). 若该区间内存在x*， 使得一阶导数等于零且二阶导数小于零， 则插值函数fi(x)在x*处取得局部最大值， 即为凸峰. 得到整条拟合曲线的所有局部最大值， 记为 (xi,yi) (i= 1, 2,m)， 并假设其高度服从某种分布(如高斯分布). 根据数据集 (xi,yi) 可以求得分布函数的参数， 从而确定其凸峰高度分布函数.

1.3 峰顶曲率半径

赫兹接触理论中， 凸峰的曲率半径与该点载荷、 接触面积以及塑性变形指数等有密切关系. 因此， 需要知道每一个峰顶的曲率半径. 可根据公式(3)， 求解出插值函数fi(x)各个局部最高点的曲率半径值，

(3)

1.4 凸峰密度

凸峰密度是指单位面积上的凸峰数目， 是GW接触模型中计算接触面积和载荷的关键参数之一. 通常可认为表面为各向同性， 因此可以根据凸峰的线密度来推测其面密度. 寻找出整条拟合曲线的所有凸峰后， 计算单位长度上的凸峰数目nl( 个 / mm)， 取其平方， 即获得单位面积的凸峰数目n( 个 / mm2).

2 测量实验与分析

2.1 粗糙表面形貌测量

使用如图2所示的Taylor Hobson Form Talysurf i120轮廓仪， 测量粗糙度标准样块(平磨、 外磨、 立铣、 平铣、 车削、 刨削)的表面轮廓数据. 选取采样长度为5 mm， 采样间隔为125 nm， 每个样块测量三次.

图2 表面形貌测量实验Fig.2 Experiment for rough surfaces test

实际表面轮廓是由粗糙度、 波纹度和形状误差组成的[9]. 根据ISO 11562标准[10]， 采用零相移高斯滤波对表面轮廓进行处理. 高斯权函数的定义为

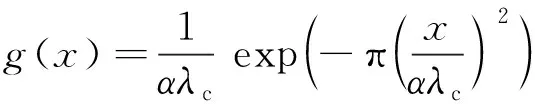
(4)

式中：λc是截止波长， 可根据ISO 4288—1996选择；α是常数， 通常取α=0.469 7.

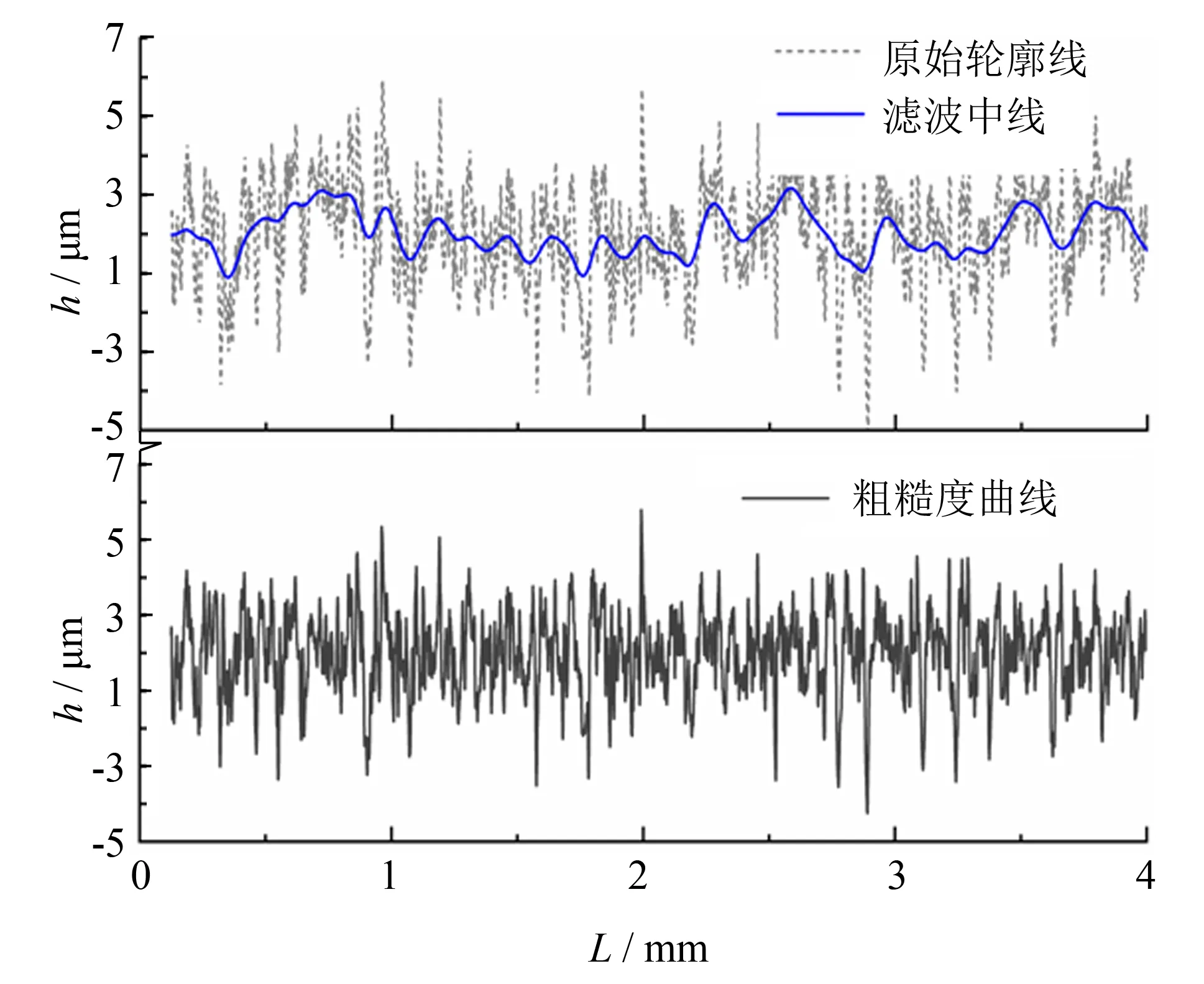
图3 表面轮廓曲线与高斯滤波中线Fig.3 Contour curve and Gaussian filter center line

若实际表面轮廓为z(x)， 信号长度为N， 高频粗糙度信号为r(x)， 低频基准信号为w(x). 通过表面轮廓z(x)与高斯权函数g(x)进行离散卷积运算， 将粗糙度信号r(x)从中分离出来[11].

(5)

r(x)=z(x)-w(x)

(6)

以粗糙度为Ra=0.8 μm端铣加工的标准样块为例. 通过高斯滤波得到的基准线是一条连续曲线， 如图3所示. 包含于原始轮廓中， 粗糙度轮廓曲线为原始轮廓线减去高斯滤波中线， 能够比较准确地反映其粗糙度特性.

2.2 表面粗糙度计算与分析

轮廓曲线高度参数用于表达一维形貌. 其最常用的是轮廓算术平均偏差Ra

(7)

式中：zi是各测试点相对于平均线的高度；n是测试点数， 一般由评估长度和采样间隔来确定[10].

根据式(7)分别计算不同机加工方法下， 不同表面粗糙度标准样块的Ra值， 将得到的实测值与标准值进行比较， 其结果如表1所示. 由表1可见， 根据ISO 11562标准推荐的滤波算法和截至波长λc得到的Ra实测值与标定值误差均在3%以内. 对比结果表明， 采样得到的形貌数据能够较真实地反应实际形貌.

表1 表面粗糙度实测值与标定值比较

3 结果与讨论

3.1 凸峰曲率半径对比分析

由式(3)可知， 根据峰顶的一阶和二阶导数可求得该点的曲率半径. 以外圆磨加工、 粗糙度Ra=0.8 μm的标准样块为例， 峰顶曲率半径分布直方图如图4所示. 实际上每一个峰顶的曲率半径不尽相同， 但其值往往会集中在某一值附近. 为便于计算， 在实际应用中往往取其平均值， 即

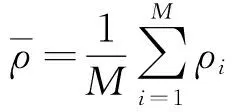
(8)

对比了不同加工方法、 不同Ra值标准样块表面形貌的凸峰曲率半径， 如图5所示. 由图5可见， 采用相同加工方法， 随着表面粗糙值的增大， 表面凸峰的平均曲率半径也相应增大. 如同样是车削的加工方法，Ra为0.8和6.3 μm时， 其平局曲率相差约为6倍. 其主要原因为采用表面粗糙度衡量微观不平整性， 粗糙度值越大， 表面起伏越明显， 较高凸峰上易生成较小凸峰， 根据本算法， 较高凸峰周边的凸峰会合并为单个的新凸峰， 因此拟合得到的曲率半径将变大， 导致平均曲率半径随着粗糙度的增加而变大. 在相同Ra值的情况下， 如同为Ra= 0.8 μm， 铣、 车和刨加工表面形貌凸峰的平均曲率分别为0.55、 0.53和0.51. 说明加工方法对平均曲率半径影响并不显著.

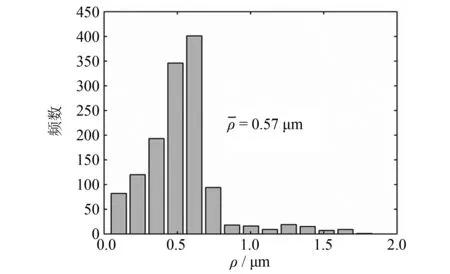
图4 峰顶曲率半径直方图(Ra=0.8 μm)Fig.4 Histogram of curvature radius for peaks(Ra=0.8 μm)

3.2 凸峰密度对比分析

计算不同加工方法、 不同Ra值的样块单位长度上的“凸峰”数， 取其平方， 得到凸峰密度. 车、 铣和刨加工， 不同Ra值标准样块表面形貌的凸峰密度对比如图6所示. 随着Ra值的增大， 离表面平均线越远的点更容易形成“凸峰”， 而凸峰周边的点形成另一个“凸峰”的机会将更小， 因此， 三种加工方法均表现为， 凸峰密度都随着Ra值的变小而增大. 在相同Ra值下比较几种加工方法的样件. 可以发现： 铣削加工方法得到的凸峰密度大于车削， 车削的大于刨削的. 相对来说, 刨削加工表面的痕迹较为明显、 车削次之、 铣削较小. 加工痕迹明显， 意味着表面形貌的采样点更容易聚集在某凸峰附近， 导致凸峰点数变少.

3.3 凸峰高度分布曲线对比分析

凸峰高度分布是指各峰顶相对于平均线的高度分布特性. 通过统计高度分布的直方图， 再拟合直方图便可得到近似的高度分布曲线. 以外圆磨加工， 粗糙度为Ra=0.8 μm的标准样块为例， 其凸峰高度直方图和分布曲线如图7所示， 凸峰高度分布曲线呈钟型， 两头低， 中间高， 左右对称， 近似于高斯分布.

图6 不同加工方法下的表面形貌的凸峰密度Fig.6 Peaks density by different processing methods

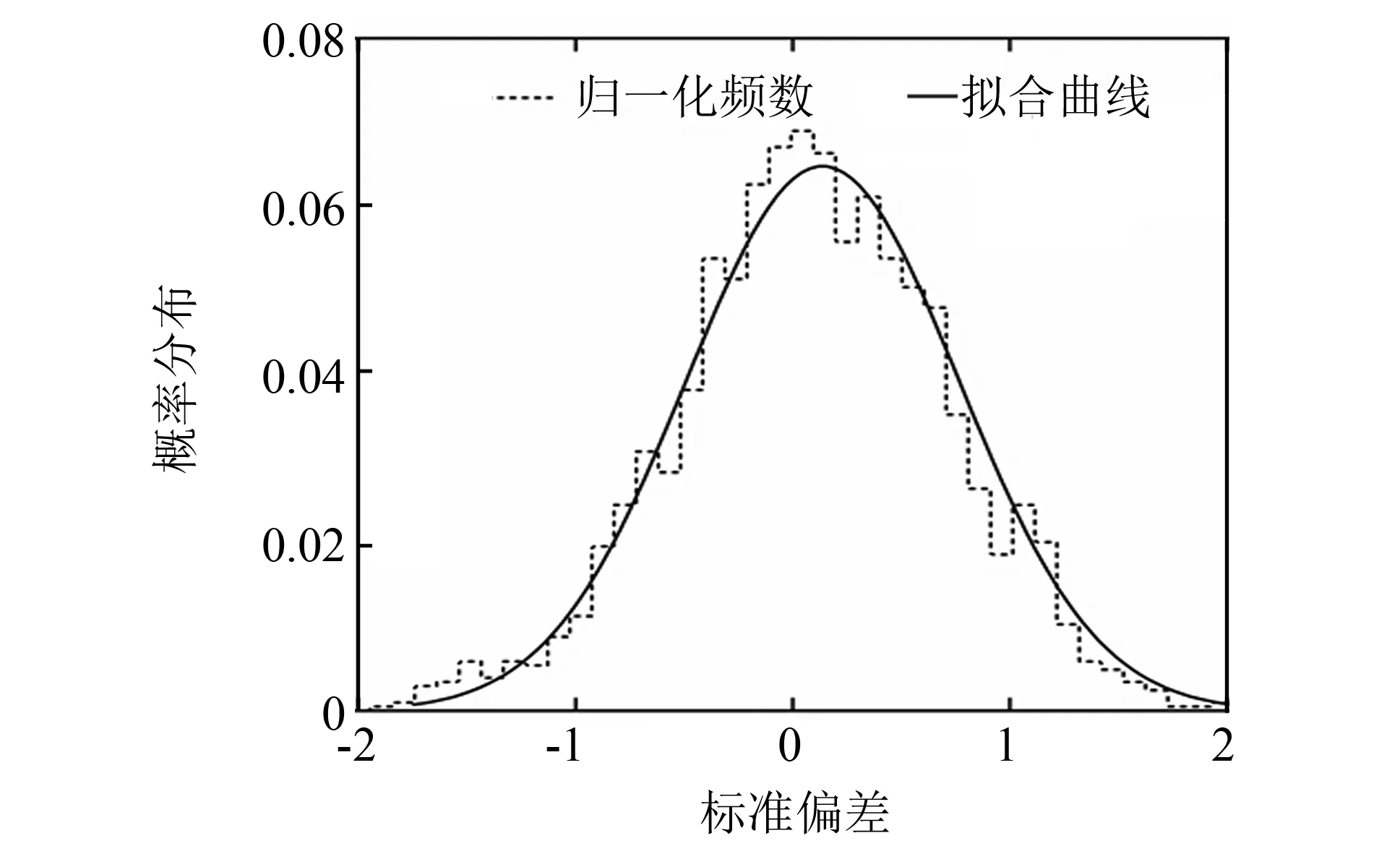
图7 凸峰高度直方图与分布曲线(Ra=0.8 μm)Fig.7 Histogram and distribution curve of peaks height(Ra=0.8 μm)

为揭示粗糙度参数和加工方法对高度分布的影响， 对不同类型的凸峰高度分布曲线进行比较. 车削加工不同Ra值样件的表面凸峰高度分布曲线如图8所示， 高度分布曲线皆近似地服从高斯分布. 由于Ra值的增大， 凸峰高度分布的区间就越大， 且总的凸峰数量也越小， 因此其标准偏差也越大， 造成高度分布曲线越平坦.

不同加工方法Ra均为1.6 μm的标准样件的表面凸峰高度分布曲线如图9所示. 可以看到， 分布曲线均近似于高斯分布， 但不同的加工方法对应曲线的标准差会有所不同， 其标准差由小到大的次序分别为： 铣、 车、 刨. 标准差小的， 表明分布更加集中， 其加工精度更高， 工件的表面质量更好. 与表面凸峰密度分布特点类似， 相对于车与刨来说， 铣削加工方法得到的表面加工痕迹相对较不明显， 固其凸峰高度分布曲线的标准差也相对较小.

图8 不同Ra值的凸峰高度分布曲线Fig.8 Peak height distribution curve for different Ra

图9 不同加工方法下的凸峰高度分布曲线Fig.9 Peak height distribution curve for different processing methods

4 结语

1) 基于曲线拟合理论定义凸峰的方法， 可以更快速和简便地得到粗糙表面形貌统计参数， 可应用于粗糙表面接触分析. 同时， 本方法可以确定每个凸峰的位置、 高曲率半径等信息， 从而避免“等半径”和服从高度分布函数的人为假设以开展粗糙表面接触的数值分析.

2) 对典型加工方法得到表面的形貌统计参数定量分析可知， 粗糙度值对平均曲率半径、 高度分布函数和凸峰密度的影响显著； 粗糙度Ra值越大， 表面形貌的平均曲率半径越大， 单位面积凸峰点数越少， 其轮廓高度值分布得越分散， 高度分布曲线越平缓.

3) 相同Ra值， 不同机加工表面形貌的平均曲率半径和凸峰高度分布曲线各不相同. 总体来说， 磨削和铣削加工表面的凸峰密度相对较大， 凸峰高度分布曲线的方差相对较小， 但加工方法对平均曲率半径影响并不显著. 因此， 采用统计参数分析表面接触刚度、 接触热阻、 实际接触面积以及弹塑性比等特性时， 应考虑加工方法和粗糙值的影响.