采用Cattaneo-Christov热通量模型的Casson流体流动研究

许晓勤, 陈淑梅, 林绍义

(1. 福建船政交通职业学院汽车运用工程系， 福建 福州 350007； 2. 福州大学机械工程及自动化学院， 福建 福州 350108)

0 引言

非牛顿流体在工程和工业中有着广泛的应用， 例如聚合物溶液、 钻井泥浆、 油漆、 番茄酱、 洗发水等流体均不服从牛顿粘滞定律， 其应力和应变率之间的关系是非线性的. 不同场合的非牛顿流体控制方程更加复杂且不尽相同， 近年来比较流行的非牛顿流体模型主要有Maxwell流体、 Williamson流体、 粘弹性流体、 切线双曲流体等. 其中Casson流体是最常见的非牛顿流体流变模型之一， 能成功描述血液、 果汁、 汤、 酱油、 巧克力等非线性流变行为. 如Sankar等[1]在分析通过狭窄动脉的血流脉动情况时就将血液看作Casson流体， 而将周围的血浆看作牛顿流体处理； Cikrikci等[2]在研究低热量巧克力配方的物理特性时也认为Casson模型最能拟合不同巧克力配方的流变数据.

由拉伸板运动产生的非牛顿流体流动在实际生产中也广泛存在， 如通过狭缝挤出熔融聚合物、 塑料片生产、 食品加工、 造纸、 电线和纤维涂层等. 在这些过程中， 产品的最终质量在很大程度上取决于传热过程中的冷却速率， 而磁流体动力学(magnetohydrodynamic， MHD)参数是控制冷却速率， 获得所需产品质量的重要参数之一[3]. 这也是广大学者研究的热点问题之一， 如Nadeem等[4]研究在热辐射存在下， 指数收缩板引起的Casson流体MHD流动与传热； Mukhopadyay等[5]研究在给定热通量条件下， 指数拉伸板引起的Casson流体稳态MHD边界层流动与热传递. 结果均表明磁场能够抑制速度场而增大温度场.

当两个接触物体或同一物体温度不同时， 就会产生热交换， 过去主要采用傅立叶定律来描述. 傅立叶热传导定律给出的是抛物线方程， 意味着任何初始温度变化均会瞬间被整个物体感受到， 而这与实际并不相符[6]. 为了解决这个问题， Cattaneo[7]在傅立叶热传导定律基础上引入热松弛时间， 认为热是以低速热波的形式传递. 随后， Christov[8]利用热松弛时间及Oldroyd上对流导数修正了Cattaneo定律(即后来学者们经常提到的Cattaneo-Christov热通量模型)， 以保持模型的材料不变性. 近年来， Cattaneo-Christov热通量模型在各种物理场合的应用研究引起了越来越多学者的关注. Hayat等[9]研究了在Cattaneo-Christov热通量存在时， 双扩散效应对3D纳米流体流动的影响； Mustafa[10]探讨拉伸板引起的粘弹性流体旋转流动与传热， 采用Cattaneo-Christov热通量模型； Mahmood等[11]分析Casson纳米流体边界层流动的熵产与传热现象， 热传导模型采用Cattaneo-Christov热通量形式.

受上述文献启发， 本文旨在研究由线性拉伸板引起的Casson流体作磁流体流动时的边界层流动与传热现象， 热传导方程采用Cattaneo-Christov热通量模型, 能量方程采用Cattaneo-Christov热通量模型. 利用打靶法， 结合龙格库塔法和牛顿迭代法数值计算, 用图形详细分析各控制参数对速度、 温度及表面摩擦系数、 局部Nusselt数的影响. 并与经典的傅立叶热传导定律进行对比分析. 最后文章还给出了Casson参数和磁场参数对流体流动和传热的影响.

1 数学模型

图1 Casson流体流动示意图 Fig.1 Schematic of Casson fluid flow

研究不可压缩Casson流体在拉伸表面上的磁流体流动， 考虑了Cattaneo-Christov热通量形式， 施加的磁场为恒定磁场B0. 采用笛卡尔坐标系，x轴平行于拉伸表面,y轴垂直于拉伸表面， 如图1所示. Casson流体作各向同性、 不可压缩流动时的流变状态方程为[12]：

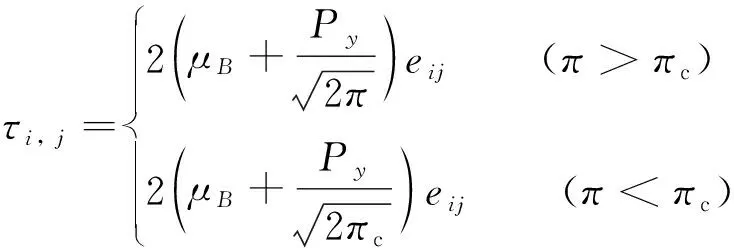
(1)

式中：μB为非牛顿流体的塑性动力学粘度；Py为流体的屈服应力；eij为(i，j)变形率分量；π=eijeij为变形率分量的自乘量；πc为基于非牛顿模型变形率分量自乘量的临界值.

由质量守恒定律、 动量守恒定理及能量守恒定律可得如下边界层方程：

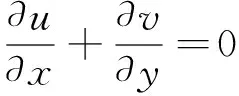
(2)

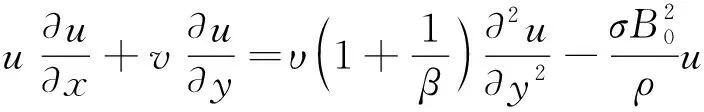
(3)

(4)

边界条件：

u=uw(x)=cx,v=0,T=Tw(y=0)

(5)

u→0,T→T∞(y→∞)

(6)

引入下列相似变量：

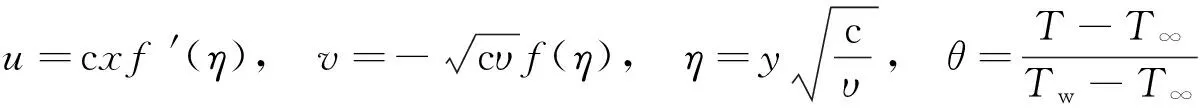
(7)

将式(7)代入方程(2)～(4)， 可知方程(2)自动满足， 方程(3)～(4)简化为：

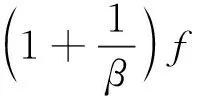
(8)

θ″+Prfθ′-λ0Pr(f2θ″+ff′θ′)=0

(9)

边界条件(5)～(6)转化为：

f=0,f′=1,θ=1 (η=0)

(10)

f′→0,θ→0 (η→∞)

(11)

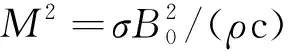
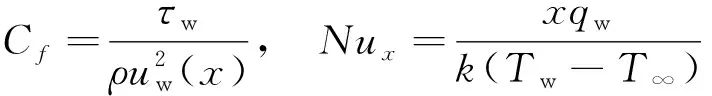
(12)

此处沿拉伸板表面摩擦力τw、 热通量qw分别定义为：

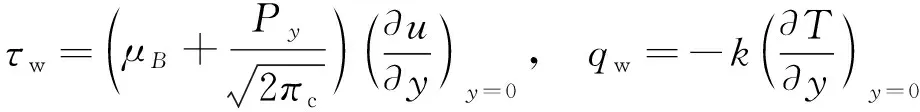
(13)

将式(13)代入式(12)得：

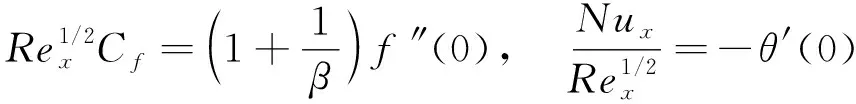
(14)

其中:Rex=uwx/υ为局部Reynolds数. 因此(1+1/β)f″(0)可代表表面摩擦系数， 而θ′(0)可代表局部Nusselt数.

2 数值方法

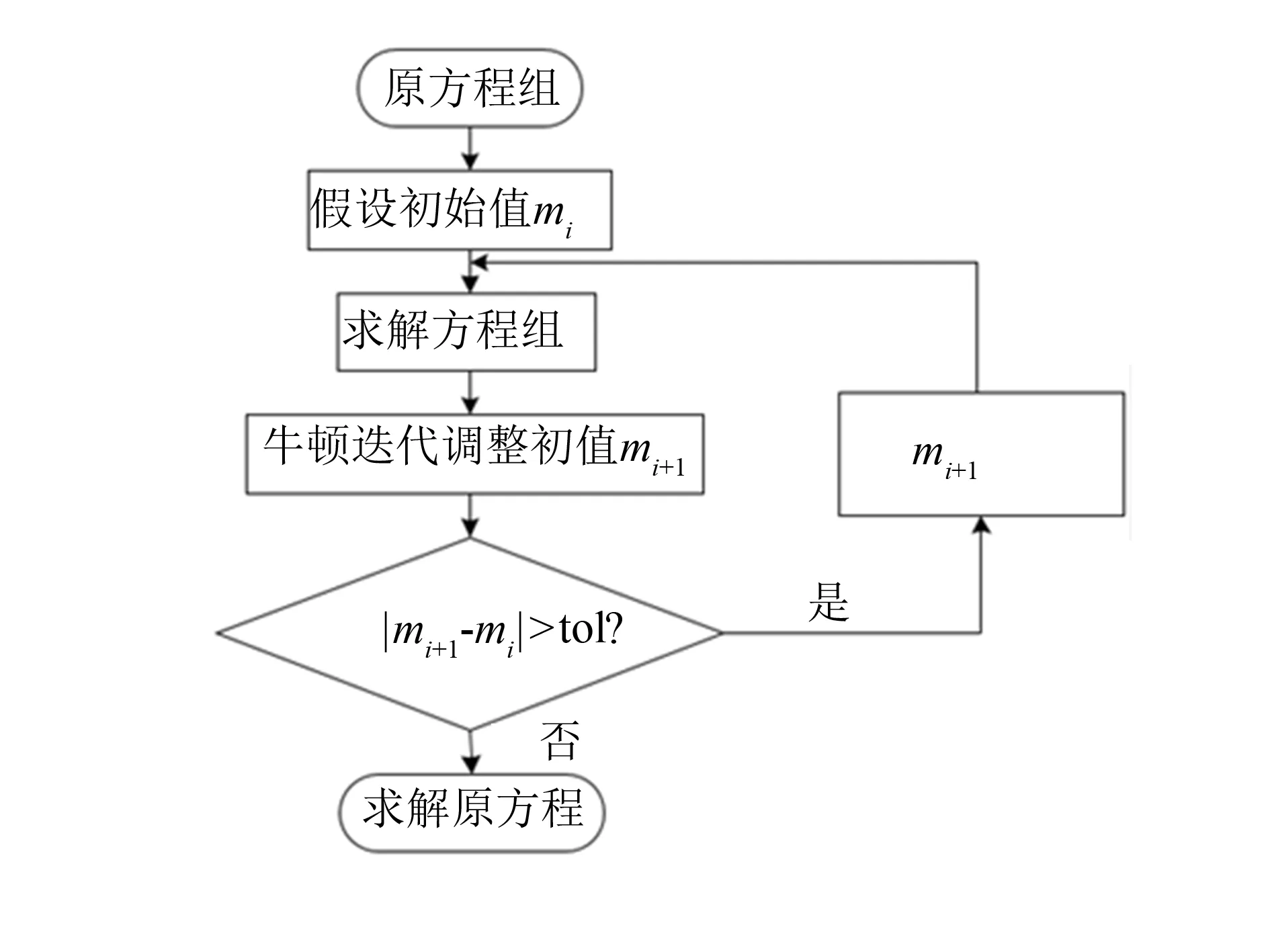
图2 程序框图Fig.2 Block diagram

上述非线性微分方程的求解采用龙格库塔法， 在Matlab程序包中结合ode45算法求解. 首先通过打靶法将边值问题转化成初值问题， 假设初始值的未知参数， 通过参数赋值后采用龙格库塔法求解， 通过牛顿迭代法不断地调整未知参数的值， 直到方程的解满足精度要求.

龙格-库塔法是求解常微分初值问题的一种重要方法， 其特点是精度高、 收敛性及稳定性好、 计算过程可改变步长等， 是目前求解初值问题的一种有效方法. 为进一步提高计算效率和计算精度， 同时采用打靶法， 其实质是将边值问题转化成初值问题来求解， 基本思想是将边值问题中未知的初始值设为未知参数， 从而将此问题看作是带有未知参数的初值问题. 文章设置误差极限为10-5， 边界层厚度η∞取有限值10， 整个过程运用Matlab编写程序代码进行迭代求解， 程序框图如图2所示. 为验证该数值方法的准确性， 将表面摩擦力-f″(0)和局部Nusselt数-θ′(0)与现有文献结果进行比较， 结果很吻合， 如表1～2所示.

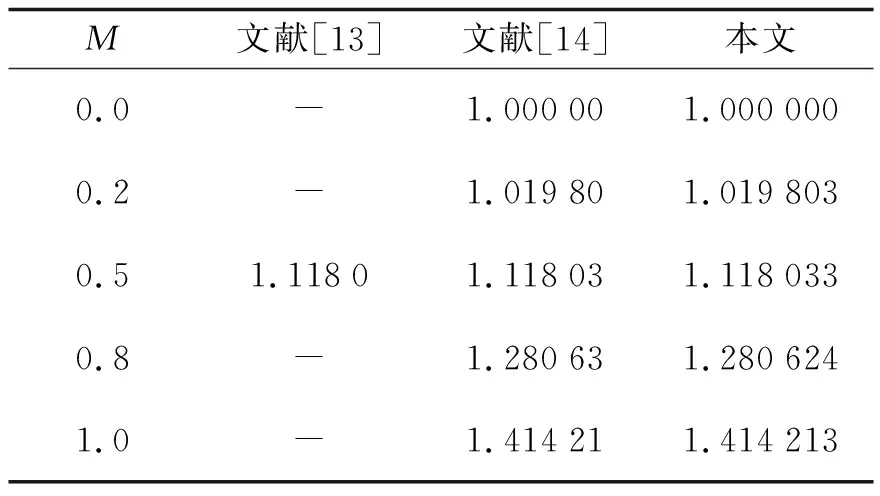
表1 M取不同值时的-f ″(0)

表2 Pr取不同值时的-θ′(0)

3 结果讨论

图3给出Casson参数β对速度和温度分布的影响， 由图可知， 速度轮廓随着Casson参数的增大而下降， 而温度变化趋势却相反. 这是因为β越大， 塑性动力学粘度越大， 阻碍流体流动， 同时粘度增加使传热加快， 从而使温度上升.

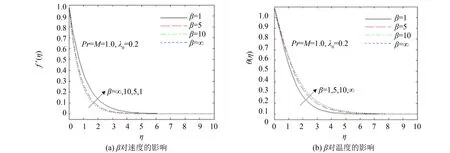
图3 Casson参数β对速度轮廓和温度分布的影响Fig.3 Effects of Casson parameters β on the velocity profiles and temperature distributions

图4给出Hartmann数M对速度和温度分布的影响， 由图4(a)可知， 速度和边界层厚度随着M的增大而减小， 这是因为磁场的上升会产生与流动方向相反的力(洛伦磁力)， 阻碍流体流动， 使速度分布减小. 由图4(b)可知， 温度的变化趋势与速度相反， 这是因为洛伦磁力会产生焦耳热， 使温度增加. 因此磁场可以控制冷却速率， 改善产品最终质量.

图4 Hartmann数M对速度轮廓和温度分布的影响Fig.4 Effects of Hartmann number M on the velocity profiles and temperature distributions

图5给出Prandtl数Pr和热松弛参数λ0对温度分布的影响， 由图5(a)可知， 温度分布及其边界层厚度随Prandtl数的增大而下降， 这是因为Prandtl数越大， 热扩散系数越小， 热扩散速度越慢， 限制温度的升高. 由图5(b)可知， 随着热松弛参数λ0的增大， 温度也下降且边界层变薄， 从物理层面解释， 热松弛参数越大， 材料颗粒将热量传递到相邻颗粒所需的时间越长， 从而降低了温度. 值得一提的是， 当热松弛参数λ0=0时， 热通量表达式与经典傅立叶热传导定律相同. 因此与采用经典的傅立叶热传导定律相比， 采用Cattaneo-Christov热通量模型得到的温度和边界层厚度均比较低.

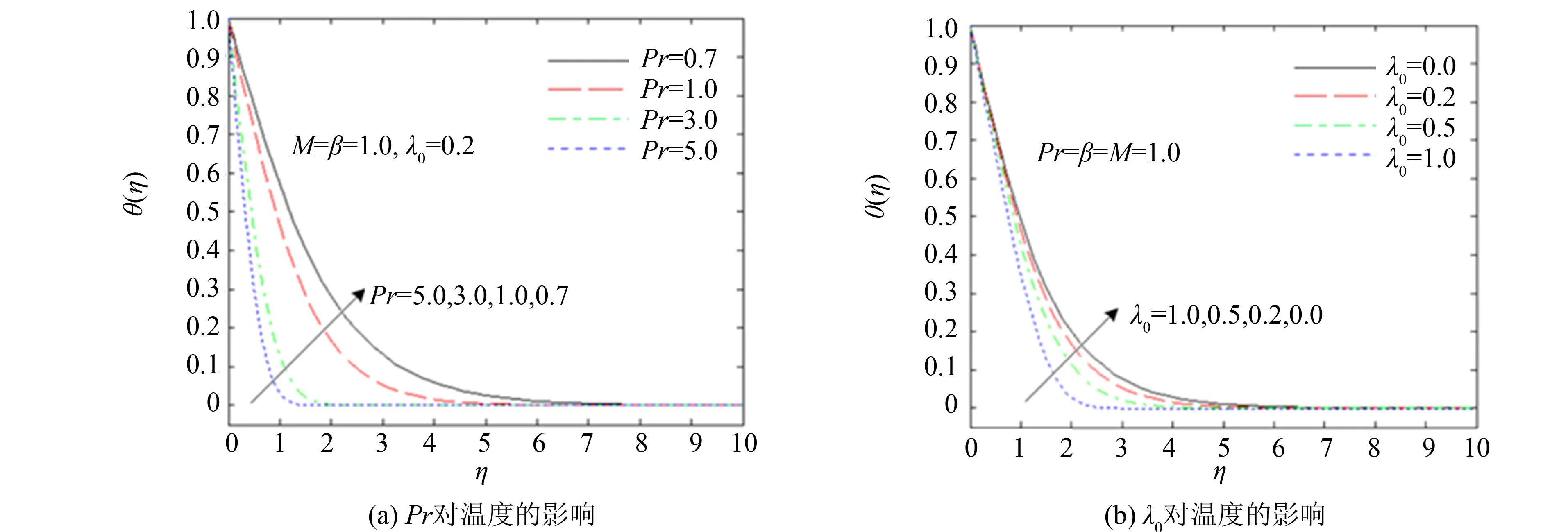
图5 Prandtl数Pr和热松弛参数λ0对温度分布的影响Fig.5 Effects of Prandtl number Pr and thermal relaxation parameter λ0 on the temperature distributions

图6给出了不考虑热松弛情况下Casson参数β和Hartmann数M对表面摩擦系数和局部Nusselt数的影响. 由图6可知， 当Hartmann数M不变时， 表面摩擦系数和局部Nusselt数均随着Casson参数β的增大而减小, 这是因为随着β值的增加， 从壁面传递给流体的热量减少， 局部Nusselt数降低. 而对于所有的Casson参数β， 表面摩擦系数均随着Hartmann数M的增大而增大， 局部Nusselt数均随着Hartmann数M的增大而减小， 这可能是由于洛伦磁力的存在增大了壁面摩擦力， 阻碍流体流动， 使流体对流传热程度减弱.

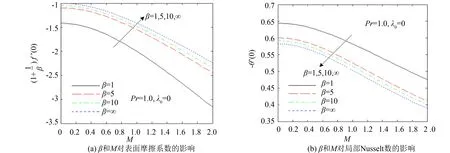
图6 Casson参数β和Hartmann数M对表面摩擦系数及局部Nusselt数的影响Fig.6 Effects of the Casson parameter β and Hartmann number M on the skin-friction coefficient and local Nusselt number

4 结语

1) 随着Casson参数或Hartmann 数的增大， 速度下降而温度上升， 通过控制磁场强度可以控制流体流动速度和冷却速率.

2) 温度随Prandtl数或热松弛参数增大而下降， 与采用经典的傅立叶热传导定律相比， 采用Cattaneo-Christov热通量模型得到的温度和边界层厚度均比较低.

3) 表面摩擦系数和局部Nusselt数均随着Casson参数β的增大而减小.

4) 表面摩擦系数随着Hartmann数M的增大而增大， 而局部Nusselt数却相反.