电动汽车再生制动与防抱死制动协调控制

周海林， 严世榕, 2， 刘 战

(1. 福州大学机械工程及自动化学院, 福建 福州 350108; 2. 闽江师范高等专科学校机电系, 福建 福州 350018)

0 引言

电动汽车的制动系统主要包括再生制动系统(regenerative braking system, RBS)与防抱死制动系统(anti-lock braking system, ABS). RBS研究的是电机制动力、 前后机械制动力的分配比例， 使电机制动回收部分能量， 执行机构有机械制动系统和电机制动系统. ABS研究的是通过控制机械制动系统使车轮运动保持在路面最佳滑移率附近. 因此， 在遇到电动汽车执行RBS时触发ABS这种情况下， 为避免两系统相互干涉， 使制动时从RBS到ABS过度平稳， 需协调这两者的控制， 这不仅能优化执行ABS时的能量回收率， 而且对维持制动安全性具有重要意义.

本田公司的Insight、 戴姆勒-克莱斯勒公司的ESX3等混合动力汽车在制动系统中对再生制动进行集成[1]. Gao[2]将制动分为轻度制动和紧急制动等不同工况， 并在车轮抱死前对机械制动力矩和电机制动力矩进行主动调节. Hara[3]的专利中， 在ABS触发前设置一个时间门限值， 当其触发时电机制动力矩按一定速率减小. Oleksowicz[4]对后驱混动车辆在ABS触发后提出三种协调控制策略： 立即终止再生制动力、 斜坡下降电机制动力至零、 斜坡下降电机轴制动力矩至一固定值. 朱雅君[5]在ABS触发预先设置减速度门限值R， 当其触发后电机制动力梯度减小. 冯亚朋[6]把再生制动按照制动强度分为小、 中、 大3类， 小强度时纯电机制动， 中等强度时混合制动， 大强度时纯液压制动， 在中等强度进入低附着路面进时， 逐步退出电机制动力矩. 张磊[7]设置不干扰制动力矩动态变化的稳定门限值， 进入ABS后电机力矩协调减压至稳定门限值以下. 李其军[8]利用电机制动对电动轮汽车进行ABS控制， 当制动强度大于电机最大制动强度， 则电液复合制动， 阶段性增加液压制动力. 郑迎[9]同样采用纯电机制动对电动轮汽车进行ABS控制， 若液压制动力矩不存在则采用纯电机制动ABS； 若液压制动力矩存在， 则保持其不再上升， 同时使用电机调节ABS. 典型ABS控制策略分为基于逻辑门限的控制与基于滑移率的控制两种， 本文主要基于滑模控制ABS对协调控制展开研究.

1 关键部件模型建模

1.1 电机制动系统与电子液压制动系统

在制动协调控制中有电机力矩与液压力矩共同参与， 故有必要对这两个执行机构动态响应进行分析建模.

虽然电机转矩响应迅速， 但传动系的转动惯量很大， 输出的电机力矩经传动系最终到达车轮的动态响应时间达不到毫秒级别. 采用一阶惯性环节来近似模拟电机动态响应特性， 其中时间常数t为150 ms.

电子液压制动系统(electro-hydraulic brake system, EHB)是ABS的执行系统， 因此有必要对EHB系统进行精确建模. 在Simulink中建立EHB模型， 其制动力矩跟随控制原理如图1所示.

图1 EHB力矩跟随控制原理图Fig.1 EHB torque following control schematic

1.2 轮胎模型建模

轮胎模型是指在制动过程中附着力与其它各种参数之间的关系， 常用的轮胎模型有魔术公式、 Burckhardt模型与双线性模型. 只考虑对纵向附着系数影响最大的因素， 采用双线性模型， 其模型表达式为：

图2 典型路面附着系数与电机稳定门限值Fig.2 Typical road surface adhesion coefficient and motor stability threshold

几种典型路面的实验参数如表1所示. 表1中四种附着系数与滑移率的关系如图2所示.

表1 典型路面实验参数

1.3 车辆动力学模型建模

图3 车辆制动动力学模型Fig.3 Vehicle braking dynamics model

研究前驱型电动汽车制动， 只需考虑车辆纵向直线运动以及车轮转动， 而不必考虑车轮转向等情况， 故将车辆简化为前后两轮的双轴模型， 如图3所示. 根据图3可得前轮制动时的动力学模型为

(1)

式中：Tbf_m为前轮电机制动力矩；Tbf_h为前轮液压制动力矩；Fzf与Fzr分别为地面对前轮与后轮的法向反作用力；μf、μr分别为前后轮的制动力系数；Fres为车辆行驶时所受到的风阻、 坡阻；r为轮胎半径；J为轮胎转动惯量. 以上公式在制动时Tbf_m、Tbf_h、Tbr_h为负值.

2 协调控制考虑因素

与传统汽车不同的是， 电动汽车进入ABS后会有多余的电机制动力矩， 故由RBS进入ABS过程中， 协调控制的目标即处理电机制动力矩， 使其不影响正常的ABS制动. 对基于滑移率控制的ABS系统， 电机力矩处理问题主要从两方面考虑. 第一， 要考虑制动能量是否回收. 在进入ABS后， 若全部把电机制动力矩退出， 虽使用机械制动会相对安全， 但不能回收能量. 我国部分南方地区降雨天气占比高达40%， 而东北地区的雨雪天气占比也达33%， 当车在这些低附着系数路面行驶时， 很容易触发防抱死控制门限， 若将电机力全部退出， 则能量都会被浪费掉； 第二， 要考虑电机制动力矩门限值的选取. 若想充分回收能量， 则需保留一些电机制动力矩， 此力矩不宜过小也不宜过大. 过小的电机力矩能量回收较少， 过大的电机制动力矩会干扰正常的液压制动执行ABS控制， 因此需选取合适的门限值， 使得电机制动力矩退出至门限值以下.

根据目前的研究现状， 门限值的选取并没有严格的理论指导， 不合适的门限值会影响制动稳定性. 另外， 考虑到不同的路面情况， 固定的门限值没有充分利用路面条件， 导致能量回收不充分. 因此， 以制动稳定性与能量回收最大化为目标进行RBS与ABS协调控制， 首先求取带有电机制动力矩时， 不影响EHB系统执行滑模控制ABS的稳定门限值， 其次根据门限值制定出合适的ABS协调控制算法.

3 ABS滑模控制分析

对带有电机制动力矩时的滑模控制ABS稳定性进行证明， 为门限值的选取打下基础.

令Fxf=Fzfμf和Fxr=Fzrμr，Fxf、Fxr分别为前轮与后轮地面制动力. 由公式(1)可得：

(2)

对前轮滑移率公式λ=1-rω/v的λ进行求导， 并将公式(2)代入可得：

(3)

(4)

(5)

4 滑模控制时的电机稳定门限值

根据滑模控制的推导， 当电机制动力矩参与制动时， ABS能正常工作， 然而实际制动中液压制动力矩会受到一定的限制， 其减压最低限制只能到0. 由于本研究采用液压制动系统作为ABS执行的动力源， 因此当电机制动力矩过大时， 进入ABS会发生两种情况： 1) 当电机制动力大于路面附着力时， 若不减小电机制动力矩， 液压制动力会一直保持为0， 滑模控制的ABS无法正常工作， 车轮会抱死. 2) 当电机制动力略低于路面附着力时， 若保持电机制动力矩， 则留给液压制动力矩变化的范围很小， 考虑到路面复杂情况以及液压制动延时等因素， 也可能导致ABS无法正常工作. 当电机制动力大于路面附着力时的ABS滑模控制的仿真如图4、 图5所示.

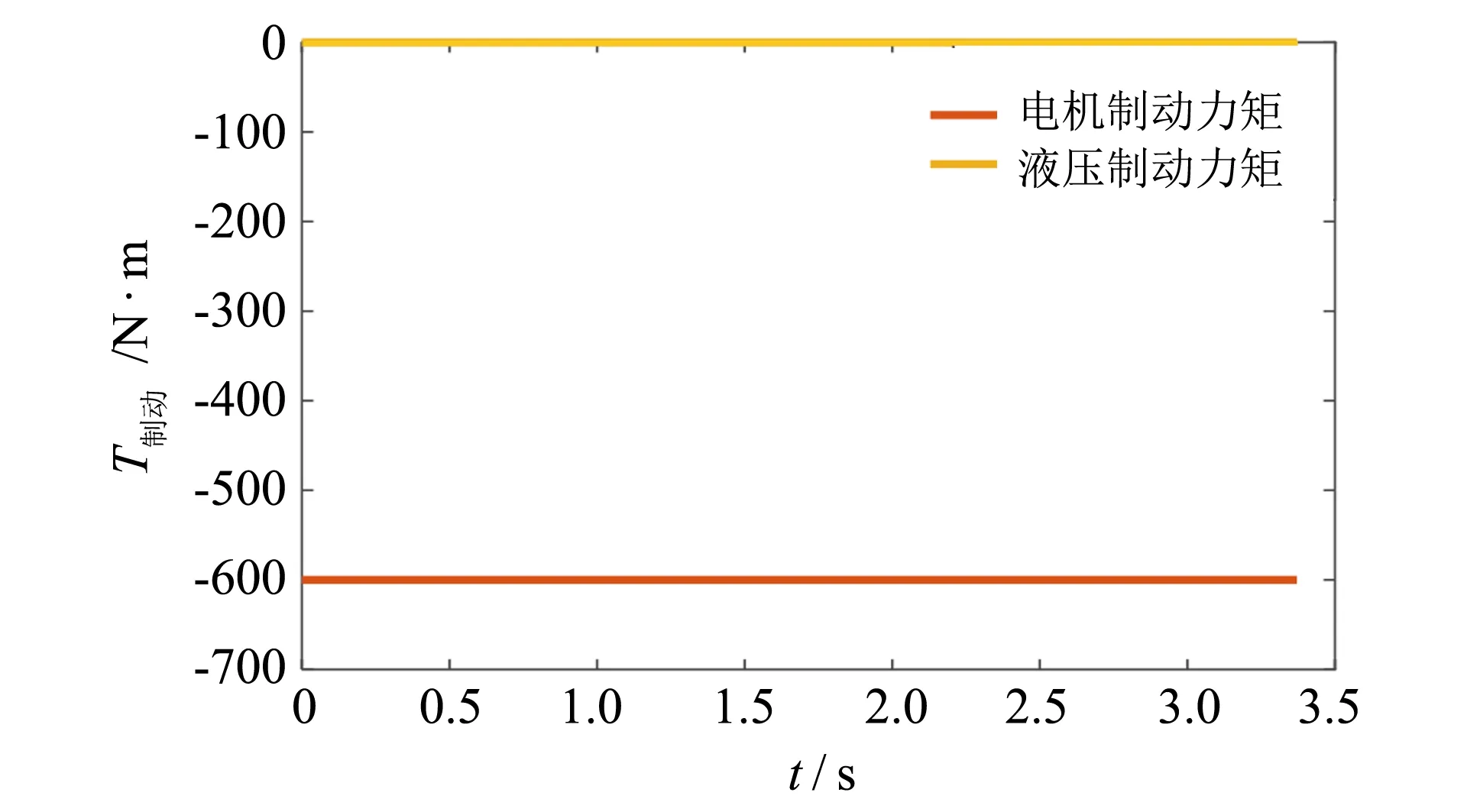
图4 液压与电机制动力矩Fig.4 Hydraulic and motor braking torque

图5 前轮滑移率Fig.5 Front wheel slip ratio

仿真路面设为湿泥土路面， 前轮路面附着力矩约为 -500 N·m. 仿真初速度为50 km·h-1， 电机制动力矩恒为-600 N·m， 电机制动力矩大于路面附着力矩， 因此滑模控制的液压制动力矩只能限制在0 N·m， ABS无法正常工作导致车轮抱死. 可见电机制动力矩需要退出至一个合理的值来维持ABS的正常工作， 此值称为电机稳定门限值.

在进行ABS控制时， 不同附着系数的路面制动力矩的变化范围也不尽相同， 若对所有的路面只限制一个电机稳定门限值， 既不合理， 也没有充分考虑利用路面条件进行能量回收的情况. 因此, 考虑到路面变化情况以及最大化回收制动能量前提下， 提出一种电机稳定门限值制定方法.

此方法为在已知最优滑移率基础上， 设置略小于最优滑移率的滑移率门限值， 将此滑移率门限值对应的路面制动力(滑移率对应的制动力系数乘以前轴重力得到的值)作为电机制动力的门限值. 这样做的优点在于能充分利用已测得的路面条件， 在保持电机制动力矩能量回收最大化的同时， 也能留给液压制动力矩一定的变化范围， 使其维持ABS的正常工作. 经仿真实验， 将略小于最优滑移率的滑移率门限值设置为： 所测得的最优滑移率值减去0.05. 以轮胎模型中四种典型路面为例， 各个路面的滑移率门限值与其相对应的制动力系数如图2的A、B、C、D点所示. 将此制动力系数乘以前轴重力即为电机制动力的门限值.

5 RBS与滑模控制ABS协调控制算法

在制定出协调控制的门限值后， 需要制定出进入ABS后的协调控制算法. 第3节证明了在进行ABS滑模控制时， 电机制动力矩的变化不影响制动稳定性， 故本研究制定的策略为： 在电机制动力矩减小的同时， 液压制动系统执行ABS滑模控制. 协调控制算法流程如图6所示.

考虑到RBS的分配策略以及路面阶跃等因素， 在进入制动模式后首先要识别路面， 并更新系统参数如路面对应的门限值. 其次判断是否触发ABS， 当触发ABS进入协调控制模块后， 判断当前电机制动力矩是否大于门限值， 若大于则在执行ABS的同时， 减小电机力矩.

图6 RBS与滑模控制ABS协调控制算法流程图Fig.6 RBS and sliding mode control ABS coordinated control algorithm flow chart

6 仿真分析

为验证协调控制算法正确性， 分别选择低附着系数路面与高附着系数路面进行仿真. 整车参数如表2所示.

表2 纯电动汽车整车基本参数

6.1 低附着系数路面仿真

低附着系数路面以湿泥土路面进行仿真， 其峰值附着系数为0.456 5， 初始车速为50 km·h-1， 驾驶员需求的制动强度z简化为在1 s内由0线性上升至0.5， 随后保持不变， 仿真结果如图7所示.

图7 低附着系数路面仿真图Fig.7 Low adhesion coefficient pavement simulation

仿真过程分为ABS触发前、 触发时、 触发后. 在触发前电液制动力矩分配方式按照RBS制定的策略进行， 本研究RBS中采用串联分配中的最大化制动力分配策略[10-11]， 因RBS不是本文研究重点， 故不再进行此过程的力矩分配介绍. 在ABS触发时， 电机制动力矩已经超出设定的电机协调门限值， 故按照协调控制策略执行电机制动力矩的减压控制. 在触发ABS后由液压制动调节滑移率， 电机制动力矩退出至门限值后则一直保持不变， 滑移率在进入ABS后一直控制在最优点， 验证了带有电机制动力矩时的滑模控制稳定性. 从SOC图可看出进入ABS后保持一定的电机制动力矩能很好地回收制动能量.

6.2 高附着系数路面仿真

高附着系数路面以干混凝土路面进行仿真， 其峰值附着系数为0.9， 初始车速为80 km·h-1， 驾驶员需求的制动强度z简化为在1 s内由0线性上升至1， 随后保持不变， 仿真结果如图8所示.

图8 高附着系数路面仿真图Fig.8 High adhesion coefficient pavement simulation

在触发ABS时， 电机制动力矩没有超出设定的电机协调门限值， 这是因为触发时速度较高， 电机工作在恒功率区域， 对应制动力矩受到外特性的限制， 同时也是因为高附着系数路面的电机协调门限值较高. 所以在触发ABS后， 将一直保持电机制动力矩不变， 由液压制动调节滑移率. 从SOC图、 滑移率图可看出， 在高附着系数路面同样验证了协调控制算法的有效性.

7 结语

对电动汽车的再生制动(RBS)与防抱死(ABS)协调控制展开相关研究. 首先分析协调控制中电机制动力矩的处理问题时需要考虑的因素， 采用滑模控制方法进行ABS控制， 验证了带有电机制动力矩时滑模控制的稳定性. 其次分析了过大的电机制动力矩会对ABS控制产生一定影响， 进而提出不影响ABS滑模控制的滑移率门限值， 并针对门限值设计了协调控制算法. 通过仿真得出： 进入ABS后电机制动力矩能很好的退出至门限值以下， 在进行液压制动力矩执行ABS控制的同时， 也保留了一部分电机制动力矩， 因此能有效地回收能量， 表明协调控制算法的正确性.