范畴的广义局部化

唐丽丹， 沈 臻

(福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

局部化也称为分式化， 是交换代数及代数几何中的重要工具[1]. 通过局部化思想， 可利用局部性质反映代数系统的整体性质. 局部化的思想近年来发展蓬勃, 文献[2-3]先后推广、 引入交换环与交换模的广义局部化； 文献[4]利用Serre类引入了Abel范畴上的局部化； 文献[5]通过épaisse子范畴构造了三角范畴的商范畴， 即局部化范畴. Abel范畴与三角范畴局部化的方法在环论、 代数表示论等多个方面都具有丰富的应用[6]. 本研究将在此基础上引入一般范畴的广义局部化的概念， 并证明加法范畴的广义局部化范畴仍是加法范畴.

1 范畴的广义局部化

定义1[7]设C是范畴，C中若干态射构成的集合S称为C的一个乘法系， 若以下条件成立：

Ⅰ)S对于态射合成是封闭的, 对任意Χ∈objC， 有1X∈S.

Ⅱ)对于C中任意态射a,s， 其中s∈S， 都存在态射c,t, 其中t∈S, 使得at=sc； 对偶地， 对于C中任意态射a,s， 其中s∈S， 都存在态射c,t， 其中t∈S, 使得ta=cs.

Ⅲ)对于C中的态射s,f,g， 若sf=sg， 其中s∈S， 则都存在t∈S， 使得ft=gt； 对偶地， 对C中的态射s,f,g， 若fs=gs， 其中s∈S， 则都存在t∈S， 使得tf=tg.

首先， 给出右分式的定义:

定义2设S、T是范畴C上的两个乘法系， 且S⊆T，X,Y∈objC. 则称态射图(图1)为从X到Y的一个右分式， 其中s∈S， 记为(b,s).

接下来， 通过介绍一些相关的引理来引出范畴的广义局部化的概念.

图1 态射图 图2 等价关系交换图 Fig.1 Diagram of morphisms Fig.2 Equivalence relation exchange graph

引理1设S、T是范畴C上的两个乘法系， 且S⊆T，X,Y∈objC.X到Y的右分式集上定义关系如下： (a,r)～(b,s)⟺存在i∈hom(C,Z1)，h∈hom(C,Z2)，u∈T， 使得ri=u=sh且ai=u′=bh， 即存在如图2的交换图. 则“～”是等价关系.

证明 由图2可知对称性显然成立， 下证自反性与传递性即可. 对任意右分式(b,s)， 存在1Z∈hom(Z,Z)，s∈S⊆T， 使得s1Z=s=s1Z且b1Z=b=b1Z， 故自反性成立.

假设(a,r)～(b,s)， (b,s)～(c,t)， 则存在交换图(图3(a)～(b))， 其中u,v∈T. 由定义1的Ⅱ)可知， 存在C中的态射x∈hom(L,C)，y∈hom(L,K)， 其中x∈T， 使得ux=vy， 则(sh)x=(sk)y， 即s(hx)=s(ky). 由定义1的Ⅲ)可知， 存在w∈S， 使得(hx)w=(ky)w， 则s(hxw)=s(kyw). 注意到有sh=u且sk=v， 所以uxw=vyw. 又有ri=u，tj=v， 所以r(ixw)=uxw=vyw=t(jyw). 同理可证，aixw=u′xw=cjyw， 这里由u,x∈T，w∈S且S⊆T可知uxw∈T， 即有交换图(图3(c)). 故(a,r)～(c,t).

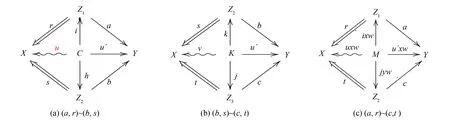
图3 引理1中传递性的交换图Fig.3 Commutative diagram of transitivity in Lemma 1

图4 右分式等价类的合成Fig.4 Composition of right roofs

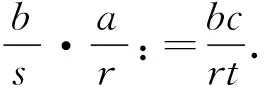
图5 引理2中1) 的证明交换图 Fig.5 Proof commutative diagram of 1) in Lemma 2

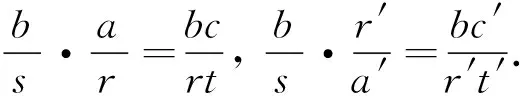
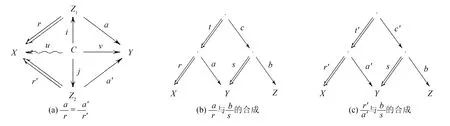
图6 引理2中2) 的证明交换图Fig.6 Proof commutative diagram of 2) in Lemma 2

3) 同理可证.

图7 引理3中的交换图Fig.7 Commutative diagram in Lemma 3

图与的合成

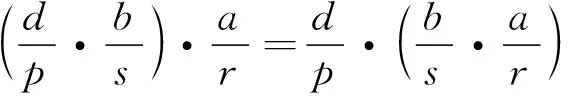
证明 假设有如图7的交换图, 则：

证明 由于图8是交换图， 如右图所示：

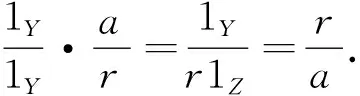
由引理2～4， 可以得到广义局部化范畴的定义.

Ⅰ) 其对象是C中的对象；

例1设R是交换环，S，T是R的乘法闭子集， 且有S⊆T， 可以定义如下：

①对象：x；

② 态射： homC(x,x)=R；

③ 态射合成定义为R中元素的乘法.

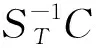
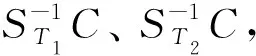
2 加法范畴的广义局部化

图9 右分式加法定义中的交换图Fig.9 Commutative diagram in the definition of additive of right roofs

引理5设(a1,p1)～(a2,p2)， (b1,p1)～(b2,p2)， 则(a1+b1,p1)～(a2+b2,p2).

证明 由已知条件存在交换图(图10(a)～(b))， 其中u,v∈T.

图10 引理5证明中的交换图Fig.10 Commutative diagram in the proof of Lemma 5

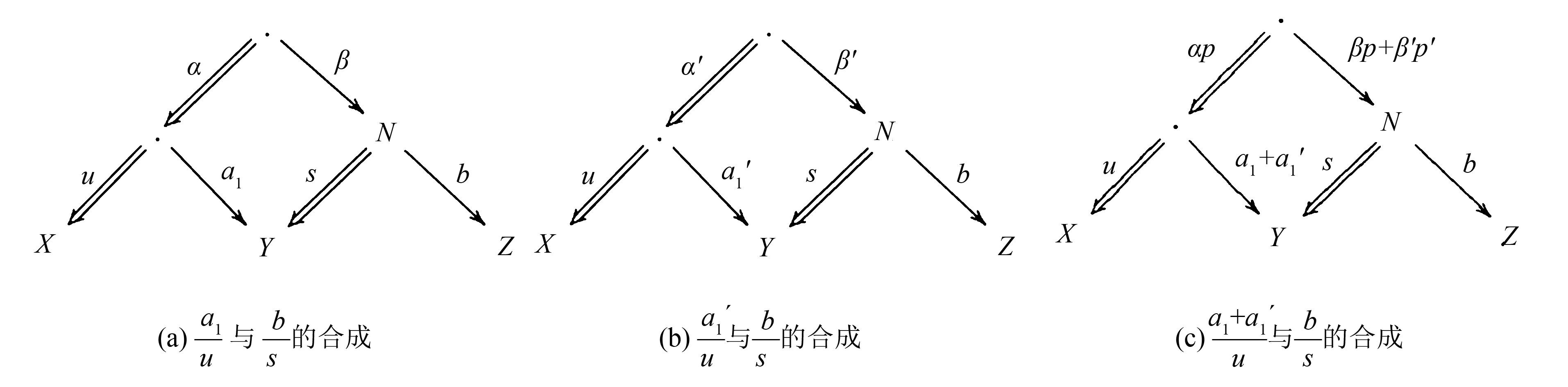
图11 引理7证明中的交换图Fig.11 Commutative diagram in the proof of Lemma 7

引理8设X1,X2∈C，X1X2是X1与X2在C中的上积，li∈homC(Xi,X1X2)是典范嵌入，πi∈homC(X1X2,Xi)为典范投影， 即πili=1Xi，πjli=0(当i≠j时)，l1π1+l2π2=1X1X2. 则是X1与X2在中的上积， 其中X1X2)为典范嵌入，为典范投影.

证明 由于存在交换图(图12(a))， 所以:

由上面的引理6～8， 可得出以下定理：

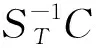
图12 引理8证明中的交换图Fig.12 Commutative diagram in the proof of Lemma 8