三角形面积公式不应该统一成一个

王亚红

三角形面积公式的推导，一般有三种（指最简洁的三种，其它忽略），第一种是拼组法（如图①），这种方法的特点是“底、高不变，面积翻倍”，所以在求三角形面积时，需要用平行四边形面积除以2，因此可得公式“三角形面积=底×高÷2”；第二种是割补法（如图②），这种方法的特点是“面积和底不变，高为一半”，所以三角形面积就是平行四边形面积，因此可得公式“三角形面积=底×（高÷2）”；第三种也是割补法（如图③），但它的特点是“面积和高不变，底为一半”，所以它可归纳为“三角形面积=（底÷2）×高”。

通过上述推导，我们可以发现这三个公式有着本质的区别，但又因为后两个可以通过“乘法结合律”或“乘法交换律”转化成“底×高÷2”，所以老师们往往喜欢把它们归纳成一个，即“三角形面积=底×高÷2”。但笔者认这样做，很不好。首先，当只有公式一个时，转化过程和空间图形都不需要想，学生计算面积时只需要套用公式，与只教结论不教过程还有什么区别。其次，不能灵活计算面积，笔者曾出过一道“已知三角形的底和高的一半，求三角形面积”的题目（如图），答案其实只需要“5.6×2”就可以了，但很多学生却还要回到统一公式，即“5.6×（2×2）÷2”。再次，不知道算式的真正意义，比如一个三角形的底是9.5cm，高是16cm，求三角形的面积。学生也都会列成9.5×（16÷2），但当问他们为什么这样列式时，他们只知道是根据公式列出来，再添加括号（目的是为了计算简便），至于是怎样的转化方式，学生却不了解。我们常说要让学生经历探究过程，积累基本活动经验，但事实已经说明大部分教师都把推导过程和积累的经验全部抛掉了。

那么怎样才能把推导过程用起来，把活动经验积累起来？笔者对此有过一些思考和实践，发现效果非常好。首先要允许学生怎样简便怎样列式，比如底7cm，高5cm的三角形，可列式为7×5÷2；底9.5cm，高16cm的三角形，可列式为9.5×（16÷2）；底10cm，高17cm的三角形，可列式为（10÷2）×17。其次要根据算式画出相应的示意图，比如7×5÷2，要画出类似于图①的图，9.5×（16÷2）要画出类似于图②的图，（10÷2）×17，要画出类似于图③的图。只有这样，才能让推导过程不断地在学生脑海中呈现，从而不断积累活动经验。

同时，笔者还把后两个公式简化成了“三角形面积=底×半高”“三角形面积=半底×高”，这与长方体的体积计算简化成“底面积×高”一样。既方便记忆，又体现了公式意义，还有利于解决“已知三角形面积和高（底），求三角形底（高）”的问题，即：三角形面积÷半高=底，三角形面积÷半底=高。

总之，不同的推导方法得出的公式所表示的意义是不同的，倘若统一成一个，则会将课堂上的探究过程将付之一炬。学生日后还要学习梯形面积、圆面积等，都可以运用这种方式，比如圆面积（如图），一个表示“长乘宽”，一个表示“正方形面积的π倍”，两者是不一样的。所以我们要认真对待每一个公式，認真解读背后的意义，只有这样，才能让学生达到灵活运用的目的，并不断地积累经验。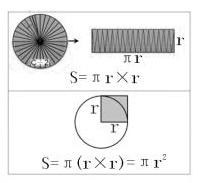

（浙江省桐乡市崇福镇留良小学）