一种基于S-R-S 构型特点的正交冗余机械臂避障规划方法
吴长征,岳 义,,韦宝琛,刘明芳
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.上海航天设备制造总厂,上海 200245)
0 引言
冗余机械臂是指关节空间维数大于任务空间维数的机械臂。由于具有冗余的自由度,机械臂在避障、避关节奇异、避关节角极限、增加特定方向的可操作度、最小化能量消耗、最小化关节力矩以及容错能力上都有优异的性能[1]。这些优点促进了冗余机械臂的广泛应用与研究。
避障规划是机器人运动规划的重要部分,也是机械臂进行自主运动的关键环节。姜力等[2]基于冗余机械臂的零空间自运动特性,利用臂型角并结合人工势场法给出了一种避障控制方法。同样是利用冗余机械臂的自运动特性,申浩宇等[3]基于协同操作雅可比矩阵提出协调避障算法。Khatib[4]于1986年最早提出了人工势场法,并将其用于移动机器人以及机械臂的避障规划,设定与目标位姿的引力场,设定与障碍物之间的斥力场,使机器人沿着势场的负梯度方向运动。Park等[5]改进了人工势场法,将其用于动态环境下的避障规划。基于零空间的方法,利用了雅可比数值迭代,需要考虑数值迭代的稳定性,人工势场法及其改进在使用过程中需要避免局部极小值带来的问题。
依托于计算机硬件性能的规划方法也受到了学者们的广泛关注。从基于搜索的规划方法,如A*方法、D*方法以及它们的改进算法ARA*(Anytime RePairing A*)等[6]方法,到基于采样的规划方法,如RRT(Rapidly Exploring Random Tree)方法、PRM(Probabilistic Roadmap)方法以及它们的改进算法T-RRT(Transition-based RRT)等[7]方法。这些方法具有很突出的规划能力,但都需要进行大量的运算。基于搜索的A*方法、D*方法适合低维度机器人,如移动机器人等,对于高维度的机械臂规划难以胜任;基于采样的方法,如RRT-CONNECT(RRT Connect)方法、PRM 方法能很好地解决高维空间的问题,但随机性很强,且同一个问题能得到多个可行解,不能保证最优轨迹;基于采样规划的改进优化方法,如RRT*[8]方法、PRM*方法能够优化得到最优轨迹,但处理效率低,甚至在指定的规划时间内难以完成求解[9]。
上述避障规划方法都有其各自适应的领域,但缺乏广泛的通用性。针对当前广泛采用的正交冗余机械臂的避障规划问题,本文利用机械臂自身的构型特点,提出一种基于S-R-S(球副-转动副-球副)构型的避障规划新方法,避免采用现有数值迭代和随机采样方法带来的问题。
1 冗余机械臂构型分析及碰撞检测模型
1.1 机械臂构型及其等效
现有的机器人厂商推出的协作型机器人大多采用正交型7 自由度冗余机械臂,如KUKA 的iiwa、ABB 的yumi、YASIKAWA 的SDA5、SCHUNK 的Lwa 4D等。本文以德国SCHUNK 公司的Lwa4D机械臂为例说明。此类型机械臂的关节配置模式如图1 所示。
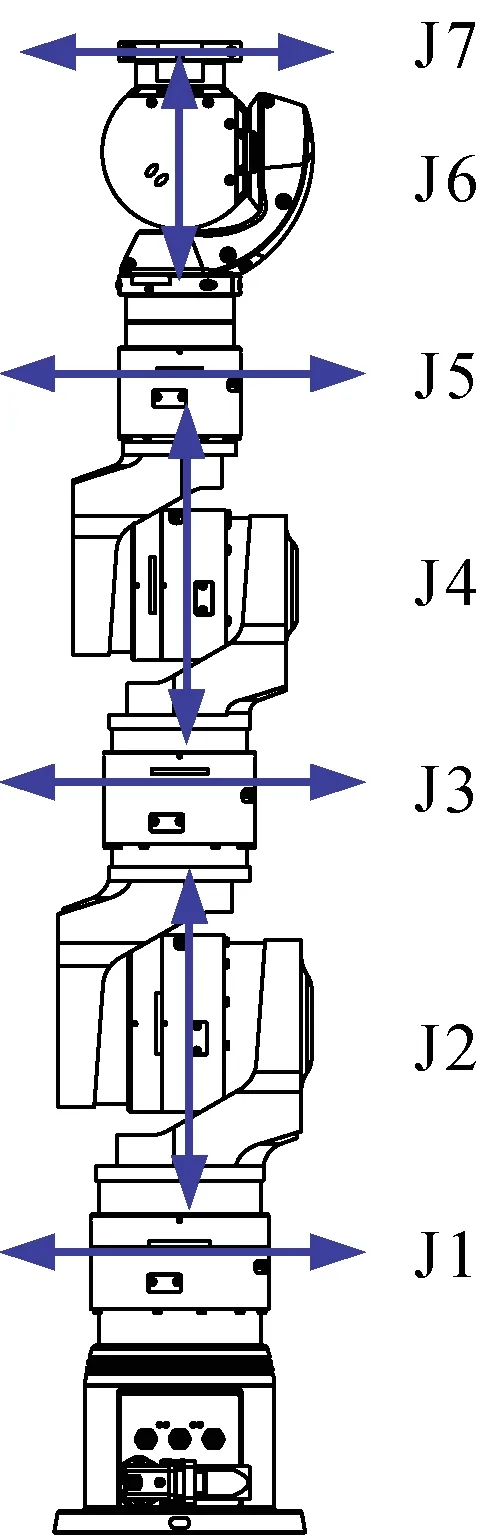
图1 Schunk-Lwa4D 机械臂的关节配置模式Fig.1 The joint configuration of the Schunk-Lwa4D manipulator
在图1中,此类型关节配置的特点为:前3 个关节(J1-J2-J3)、后3 个关节(J5-J6-J7)轴线相互垂直,配合形成球运动副。上述7 自由度正交冗余机械臂可以等效为S-R-S 构型,如图2 所示。由于存在两个等效球副,机械臂的自运动性能优越。
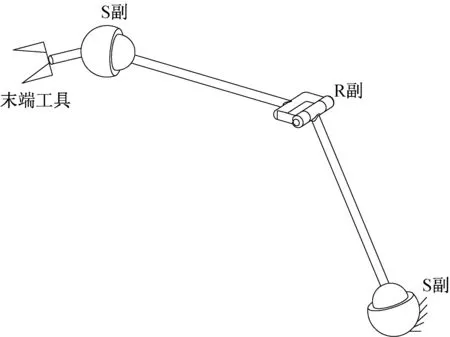
图2 等效的S-R-S 构型的机构示意图Fig.2 Schematic diagram of the equivalent S-R-S configuration
1.2 机器人杆件及环境障碍物模型
机械臂与环境障碍物的碰撞检测是进行避障规划的基础,为提升环境障碍物检测的效率,需要对环境障碍物进行预处理建模。根据包围盒原理[10],可将环境障碍物简化为圆柱体或球体两种类型,如图3 所示。这两种处理形式对计算机内存及计算资源的消耗小,同时,在碰撞检测过程中的计算量也小。相比于球体,圆柱体在空间中等效占据的体积与实物更为接近。机器人杆件以及外部障碍物一般较为规则,在本文的研究中,将机器人杆件及外部障碍物均处理成圆柱体模型。

图3 机器人杆件及环境障碍物简化模型处理Fig.3 Simplified models for the robot bars and the environmental obstacles
对机器人杆件及环境障碍物均处理为圆柱体凸体对象,多个凸体之间可以找到一个分割面,且凸体对象上两点间的距离既是局部最小值,也是全局最小值。这些性质使得圆柱体简化模型更适合作碰撞检测。
通过上述简化后,机械臂的碰撞检测等效为2个圆柱体之间的碰撞检测。2 个圆柱体上各点之间的几何关系如图4 所示。
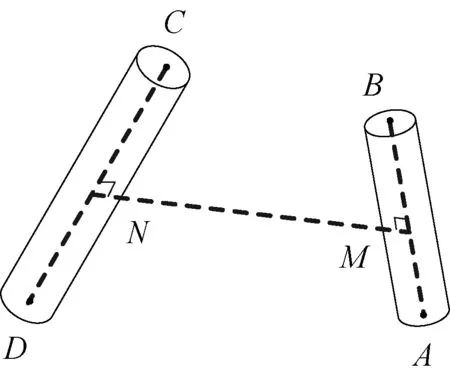
图4 碰撞检测几何关系Fig.4 Geometric relation for the collision detection
MN表示AB与CD的公垂线段,且有
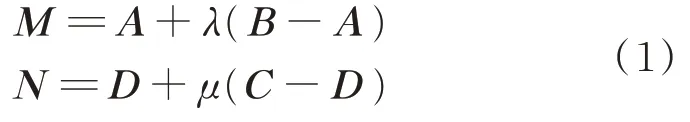
式中:{λ|λ<0或0 ≤λ≤1或λ>1},{μ|μ<0或0 ≤μ≤1或μ>1},根据λ与μ的9 种不同取值[11],得到杆件之间9 种不同的碰撞模式。
2 基于S-R-S构型特点的避障规划方法
2.1 避障规划模型
根据图2等效S-R-S 构型,可知肘部关节的位置在一个球面上,且球面区域为单连通区域。这种单连通性也能很好地映射到机械臂关节空间,球面上的连续曲线对应到关节空间同样也为连续区域。
图5为机械臂等效避障规划示意图。单臂在障碍环境中的避障规划等效于E点,在球面上的规划加上关节4(q4)的规划以及末端工具位置T的规划。可知在S点和W点均等效于一个球关节,因此,在规划完E点和q4之后,T点的规划与E点的规划类似,均为在球面上的规划。
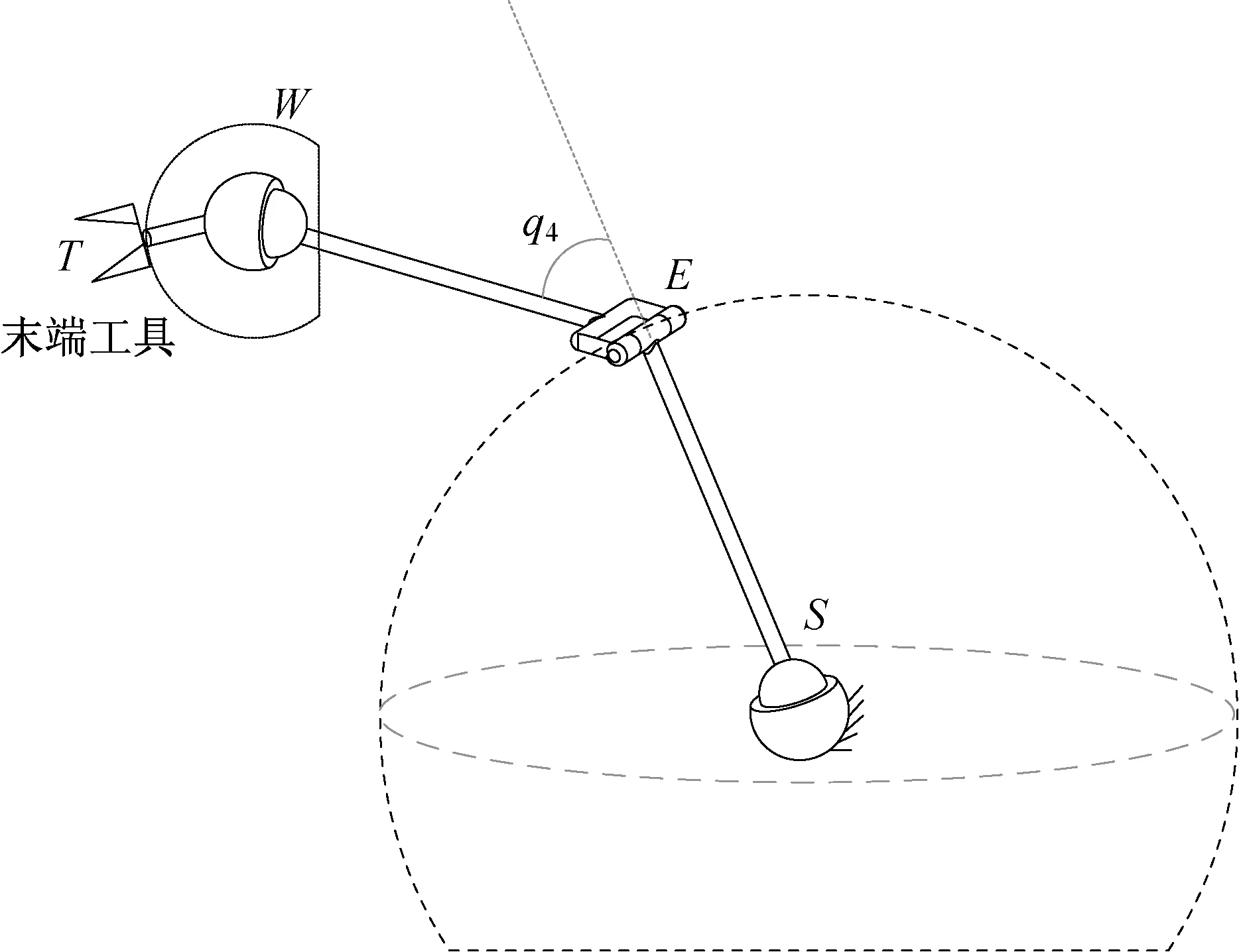
图5 机械臂等效避障规划示意图Fig.5 Schematic diagram of the equivalence obstacle avoidance planning for the manipulator
机械臂的构型为串联结构形式,前面靠近基座的关节的运动会对后面关节的状态产生影响。为排除这种强耦合的影响,将单臂的避障规划分成肘部笛卡尔位置规划、第2 根臂杆规划、末端工具规划这3 个部分依次进行。即先进行杆件SE的无碰撞规划,再进行杆件EW的无碰撞规划,最后再进行末端工具杆件WT的规划。
2.2 肘部笛卡尔位置规划
当机械臂臂杆SE与障碍物碰撞时,可以分为3种情况:1)障碍物完全在E点的可达球面内;2)障碍物一端在E点的可达球面内另一端,在可达球面外(包括在球面上);3)障碍物的两端均在可达球面外(包括在球面上)。如图6 所示为杆件SE与障碍物碰撞的3 种情况。在图6中,FG为障碍物,且S、F、G3 点必定构成一个平面。过S点作SFG的垂直平面,该垂平面与FG的交点为H点。
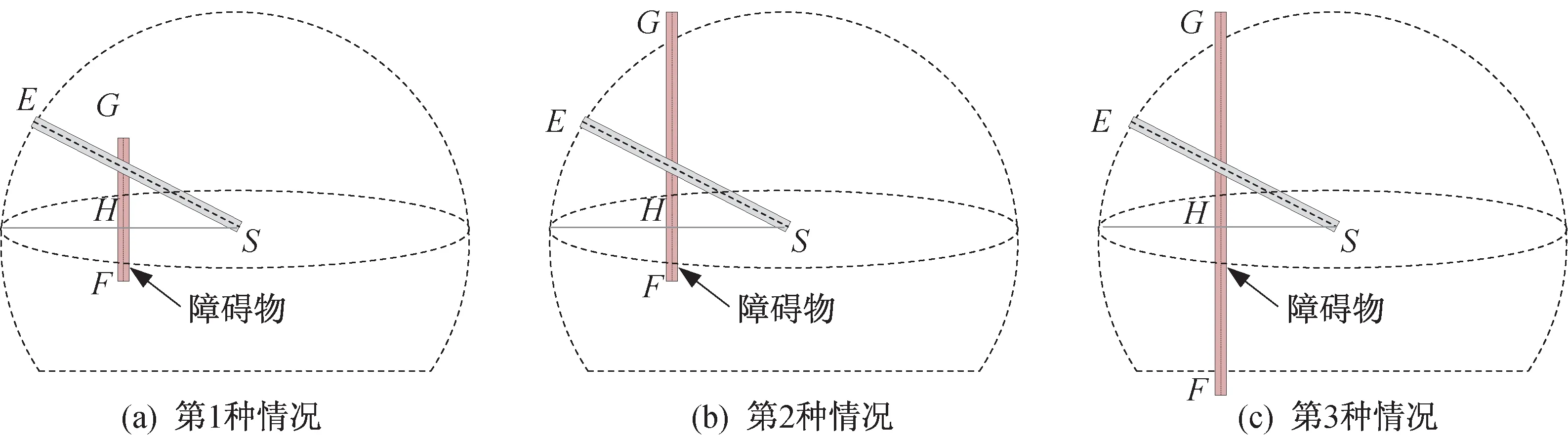
图6 杆件SE 与障碍物碰撞的3 种情况Fig.6 Three collision cases of the bar SE and the obstacle
由于臂杆SE碰撞只可能发生在可达区域球面内,上述3 种情况均可转化为图7。在图7(a)中,从球心S点向障碍物FG作射线,分别与球面相交于E′和E″点,障碍物在球面上的投影为弧段⁀所在的区域。因此,E点在球面的运动只要不经过弧段⁀,则臂杆SE便不会与障碍物发生碰撞,如图7(b)所示。则为等效的障碍物杆件。可认为杆件处于SE′和SE″均为临界碰撞状态(杆件和障碍物均已作安全距离处理),因此,只需要调整SE在SFG平面内的位置便能避开障碍物。将E′和E″点记作关键点,当∠ESE'≤∠ESE''时,避障调整的方向为朝向E′点运动避障(调整量小),反之则朝向E″点运动避障。

图7 杆件SE 碰撞情况的等效转化Fig.7 Equivalent transformation of the collision cases of the bar SE
由上得知避障调整的方向后,以过S点以FG为法线的SFG的垂平面(记为SHM)为界,仅对障碍物的其中一端作出分析(保留HG段,另一端分析方法相同)。
现在针对图8 对SE杆的避障规划作出说明。杆SE与障碍物发生碰撞的情况下才作出调整。在对障碍物和机器人杆件完成简化的基础上,障碍物的轴心线段与球心总能构成一个平面。发生碰撞时,杆件与障碍物的轴心线在此平面中相交于一点,即如图8(a)所示。由于在运动过程中,杆件SE必将会经过此平面,因此,避障需要保证杆件轴心线段SE与障碍物HG无交点。
如图8(b)所示,将实际障碍物通过相似变换为等效障碍物。不管何种情况下,总能找到等效障碍物与球面的交点,此处的交点可认为是临界无碰撞状态下的肘部的位置E′,这也是在运动过程中最有可能发生碰撞的位置,因此,将其设为关键危险点。
根据向量几何关系可得E′点的向量表达式为


图8 杆件SE 的避障规划示意图Fig.8 Schematic diagram of the obstacle avoidance planning for the bar SE
式中:norm为对向量取模操作;S为球心位置向量;G为障碍物端点位置向量;E为肘部关节点位置向量。
由于在规划过程中起始状态和终止状态均为已知,可以认为该肘部的临界无碰撞轨迹为经过球面3 点的球面曲线。在球面上进行规划,可以参考和借鉴在空间中进行多点规划,但又略有不同,其不同在于规划后的曲线上所有路径点需要满足均在球面上的约束,即肘部的杆长约束。
设定肘部的起始位置为Estart,设定肘部的终止位置为Egoal,如图9 所示。对肘部的规划转化为在球面上寻找一条经过Estart、Egoal和E'的光滑球面曲线。经过空间3 点的曲线求解有Bézier 曲线、B 样条曲线、Hermitte 插值曲线等方法。但由于肘部满足杆长约束条件,这些常用的方法不能直接使用。

图9 球面Bézier 曲线在轴平面中的投影Fig.9 Projection of the spherical Bézier curve onto the axis plane
Bézier 曲线因其具有良好的几何特性,广泛应用于计算机图形等方面。一条n次Bézier 曲线的定义为
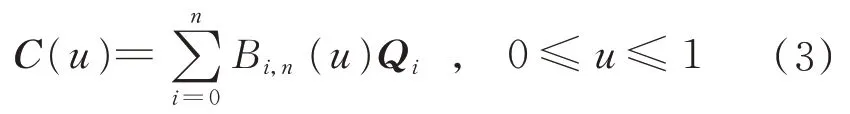
式中:Bi,n(u)为基函数,且采用n次Bernstein 多 项式[12],其定义为
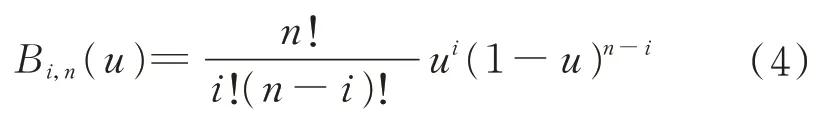
式(3)中的几何系数Qi称为控制点,用户根据需求定义,用来控制曲线的走向。式(3)和式(4)共同描述了经过空间相关点的连续曲线。本文采用3次Bézier 曲线,含有{Q0,Q1,Q2,Q3}4 个控制点。且其具有较好的性质,如其端点的切线方向平行于向量Q1−Q0和Q3−Q2,并且该曲线包含在这4 个控制点形成的凸包内。3 次Bézier 曲线的形式为
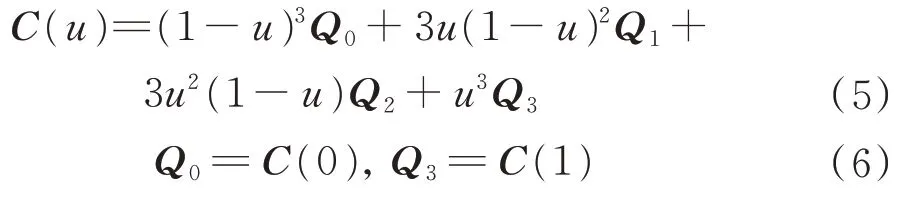
关于控制点的取法成了曲线的关键,现给出该曲线的求解方法。图9为球面Bézier 曲线在轴平面中的投影。图9中,Q0=Estart,Q3=E',Q6=Egoal。该曲线在过S点的与平面SFG和SHM的公垂平面中的投影仍然为Bézier 曲线。由于两端弧线具有一个共同点E′,此曲线共有7 个控制点。为保证曲线的光滑,需要保证在E′左右的切线方向一致,即

为保证求得的投影曲线始终在投影圆内,需要保证所有的控制点均在圆内。即

为保证曲线变化的均匀性,可以设定Q1Q2在线段EstartE′上的投影K1K2、Q4Q5,在线段EgoalE′上的投影K3K4均为1/k(k>2)处(注:图9中取在1/3 处),且Q2Q4与坐标轴平行(具体根据投影平面给出)。若在区域外,则取其与外圆的交点为相应控制点。现仅以投影面为XZ、曲线EstartE′为例说明,根据几何关系可以得到
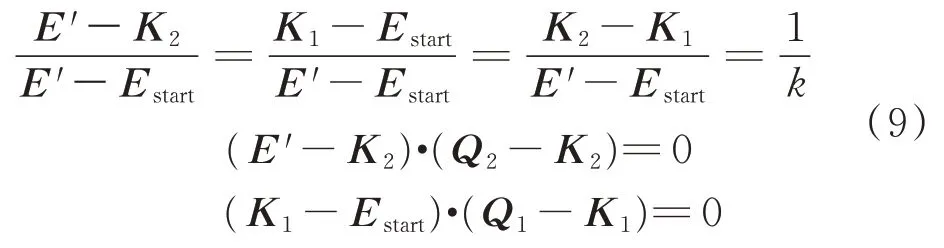
式(3)~式(9)即为肘部运动轨迹在投影面的计算公式,此时C(u)为二维坐标(C(u)x,C(u)z)。为得到球面上的三维曲线,还需作如下处理:

式中:sgn(Estart_Y)为运动轨迹点的Y轴坐标与起始点的Y轴坐标符号相同。
通过式(2)~式(10)便完成了对肘部笛卡尔位置的规划。
2.3 第2 根臂杆规划
对第2 根臂杆EW规划时,设定杆件EW发生碰撞且其他杆件不发生碰撞,此时杆SE在障碍物过球心的平面内。为使得其他杆件的运动轨迹尽量不变,可只通过调整关节角q4来避障。为使得杆件EW避开障碍物的调节最为迅速有效,此时E处的肘部(关节4)的轴线垂直于障碍物过球心的平面SHG可得到此效果。
根据图10 的避障规划示意图可知,在E处的肘部(关节4)的轴线垂直于障碍物过球心的平面时,调整杆件EW远离碰撞区域运动到临界无碰撞状态EW′,可以实现杆件EW的避障规划。杆件EW的调整方向沿着向量HG的方向。
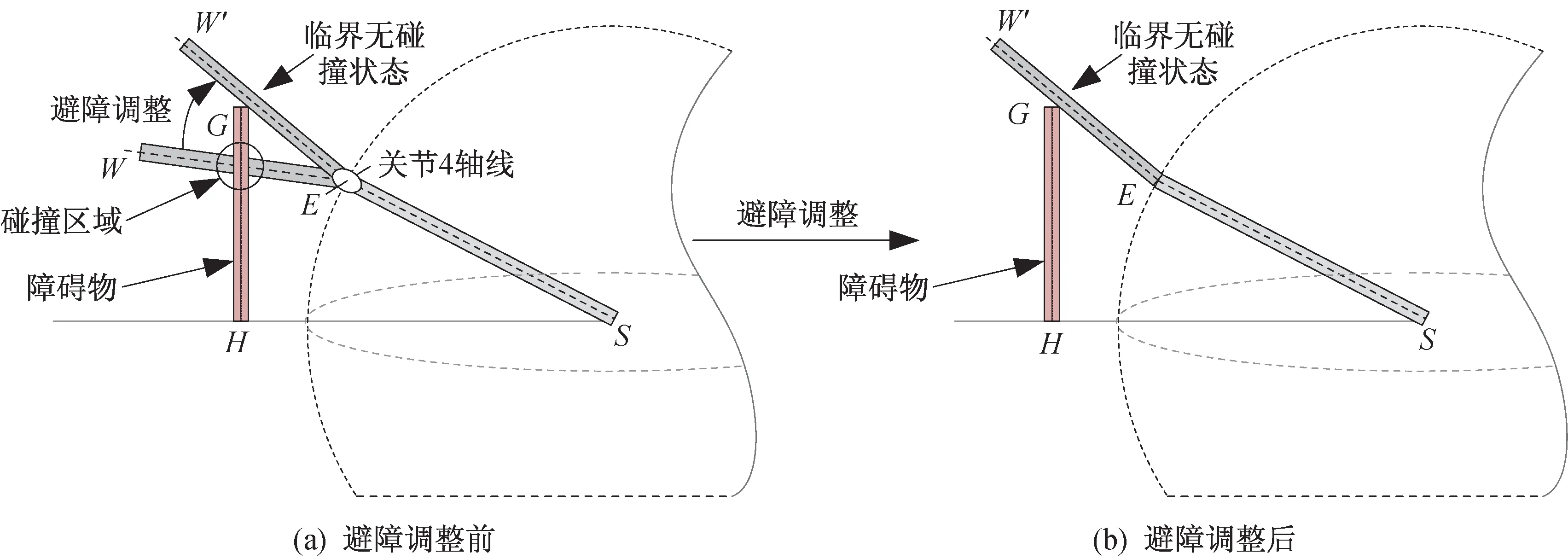
图10 杆件EW 避障规划示意图Fig.10 Schematic diagram of the obstacle avoidance panning for the bar EW
临界无碰撞状态关节4 的关节角,即为
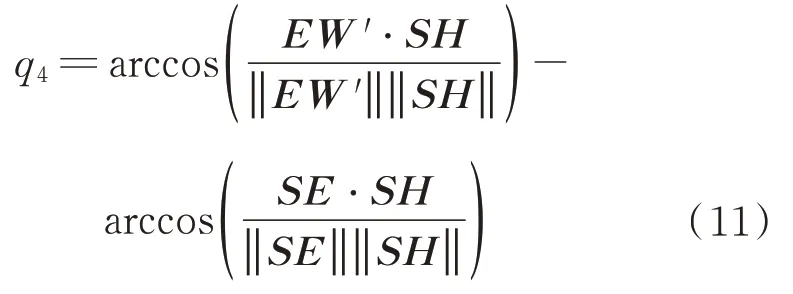
根据q4的角度值以及其轴线的方向,便能够得到机械臂在EW处于临界碰撞状态的构型。若SE杆不发生碰撞则肘部的笛卡尔轨迹无需调整,只需要调整E点姿态,使得肘部关节q4轴线为平面EHG的法线方向。
2.4 末端工具杆件规划
对杆件WT的调整规划,由于杆件WT同样等效在一个球形关节上,杆WT与SE的运动类似,均为在球面的运动,唯一不同的是WT对应的球关节在笛卡尔空间中的位置是浮动的。由于上述的避障方法是从基座开始向外扩展计算调整量的,因此,WT杆件对应的球关节在笛卡尔空间中的位置只取决于前面4 个关节的关节角。根据前面的内容可以知道,当杆件WT开始调整时,前面4 个关节角是已知的,因此,WT调整时W点的位置也是已知的,WT的调整也唯一确定。
2.5 避障规划算法总结
结合上述基于S-R-S 构型特点的避障规划3 部分,总结得到正交冗余机械臂的避障规划新方法如下(注:i表示杆件的顺序取值1、2、3)。
算法:基于S-R-S 构型特点的正交冗余机械臂避障规划方法
1)利用碰撞检测计算方法:式(1),计算危险杆件集合Φ0
2)求取i=arg min{Φ0}
3)Ifi=1
4)肘部位置规划:式(2)~式(10);从Φ0中剔除i=1→得Φ1
5)求取i=arg min{Φ1}
6)Ifi=2
7)关节4 独立规划:式(11);从Φ1中剔除i=2→得Φ2
8)求取i=arg min{Φ2}
9)Ifi=3
10)腕部位置规划:式(2)~式(10);
Endif
3 实验验证
结合Schunk-Lwa4D 机械臂,对上述提出的基于S-R-S 构型特点的避障规划新方法进行实验验证。实验时设定机械臂经过的障碍物为长方体立柱。该长方体立柱的尺寸为0.07 m×0.07 m×0.61 m。该障碍物与机械臂对应的安装位置为处于机械臂坐标系的X方位为0.45 m,Y和Z方位均为0。图11 给出了机械臂的相关尺寸以及基于S-R-S 构型特点的避障规划算法的避障过程。
图11中起始时雄克机械臂的关节角为(0.52,−1.57,0,0.09,0,0.75,0)(单位为弧度,下同),终止时的雄克机械臂的关节角为(−0.52,−1.57,0,0.09,0,0.75,0)。机械臂的肘部处会发生碰撞,此时第1 根和第2 根杆件均会会发生碰撞。
分别采用基于采样的避障规划算法RRT-con⁃nect 和基于本文提出的基于S-R-S 构型特点的避障规划算法进行试验,得到两种算法避障过程中7 个关节的关节角变化曲线。针对同一障碍物采用RRT-connect 算法进行2 次避障规划实验,得到的关节角度值变化曲线如图12 所示
采用基于S-R-S 构型特点的避障规划新方法进行避障实验,实验中雄克机械臂有效地避开了障碍物,绘制机械臂避障过程中关节角变化过程如图13所示。通过观察实验过程和记录的数据验证了基于S-R-S 构型的避障规划算法的有效性。

图12 基于RRT-connect 避障规划方法的关节角变化曲线Fig.12 Variation curves of the joint angles obtained by the obstacle avoidance planning method based on the RRTconnection

图13 基于S-R-S 构型特点的避障规划新方法的关节角变化曲线Fig.13 Variation curves of the joint angles obtained by the novel obstacle avoidance planning method based on the S-R-S configuration
由图12 可知:2 次采用RRT-connect 得到的关节运动结果不一致,且关节角变化无规律,说明了现有的基于采样的方法具有很强的随机性。
比较图12 和图13 可知:新的避障规划方法能够减少关节不必要的运动,如图13中关节3、5、7 均保持不变;采用该规划方法,机械臂有效避开了障碍物,运动唯一确定,不存在上述的随机性问题。同时图13 也验证了基于S-R-S 构型特点的避障规划新方法的有效性和可行性。
4 结束语
本文将正交7 自由度冗余机械臂构型等效为SR-S 构型,通过分析该构型的特点将机械臂的避障规划分为肘部笛卡尔位置规划、第2 根臂杆规划、末端工具规划3 个部分。利用Schunk-Lwa4D 机械臂进行了现有RRT-connect 方法和新提出的基于SR-S 特点的避障规划方法的避障实验,通过对比分析实验得到了机械臂关节角变化曲线,得到新的避障规划方法解决了基于采样规划方法的随机性问题,也验证了基于S-R-S 构型特点的避障规划新方法的有效性和可行性。后续将对扩展基于S-R-S 构型特点的避障规划新方法研究复杂环境障碍物的适用范围,并优化规划所得的轨迹。

