基于自适应IMM 算法的蛇形机动目标加速度估计研究

吴新宏，张紫琪，王 磊，高 帆，仇理宽

（1.中国人民解放军92942 部队，北京 100161；2.上海机电工程研究所，上海 201109）

0 引言

现代反舰导弹普遍采用多变弹道技术［1］结合超低空飞行进行突防，这大大提升了防空反导弹的拦截难度，对导弹制导律的快速响应性和鲁棒性提出了更高的要求。现已有诸多成熟的控制理论为制导律的设计提供了新的方向，例如，包含目标机动补偿的比例导引律、滑模变结构制导律、自抗扰控制导引律等。这些制导律在实际使用中需要获取目标的机动信息，但现有的导引头并不具备直接测量目标加速度的能力。若不对导弹加以补偿会造成较大脱靶量［4］，所以需对目标加速度进行估计。在多变弹道技术中，蛇形机动是一种典型的目标机动方式。蛇形机动是指导弹进行平面内的S 形运动，其运动轨迹形状似蛇。文献［5］探讨了蛇形机动提升导弹机动能力的有效性。文献［6］经过仿真验证了小周期高频率的蛇形机动目标更有利于提升反舰导弹的突防能力。在现役导弹中，俄罗斯的“白蛉”已具备蛇形机动的能力。

在卡尔曼滤波中，Singer 模型［7］和“当前”统计模型［8］常用来构建机动目标的运动模型，这两种模型的加速度方差受预设加速度极值的影响。目标加速度估计是由目标机动频率和加速度方差共同决定的。当目标的实际加速度大于预设加速度极值时，加速度估计精度将会下降［9］。另外，由于蛇形机动目标具有高机动性和复杂性，采用单运动模型难以描述目标的运动，因此，可用交互多模型（Inter⁃acting Multiple Model，IMM）［11］算法提升模型与真实目标的匹配性。IMM 采用多个目标运动模型，在线调整各模型匹配度，最终输出各模型滤波值的加权和为其结果。

针对以上为问题，本文改进了卡尔曼滤波算法中目标加速度方差的计算公式，建立了基于扩展卡尔曼滤波（EKF）算法的自适应交互多模型的目标加速度估计方法，实现对不同机动过载的水平蛇形机动目标的加速度估计。

1 数学模型的建立

1.1 弹-目相对运动方程

导弹和目标的相对运动方程，可用弹体执行坐标系Ox1ay1az1a和弹上视线坐标系Oxs1ys1zs1之间的转换关系来描述，弹目相对运动方程为

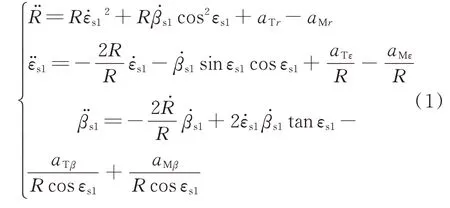
式中：R为弹目相对距离为弹目相对距离变化率；εs1为弹体视线高低角；βs1为弹体视线方位角为弹体视线高低角速率为弹体视线方位角速率；aTr、aTε、aTβ分 别为目标加 速度在坐标系Oxs1ys1zs13 个轴上的投影；aMr、aMε、aMβ分别为导弹加速度在坐标系Oxs1ys1zs13 个轴上的投影。

1.2 状态方程和量测方程

采用EKF，取状态向量为

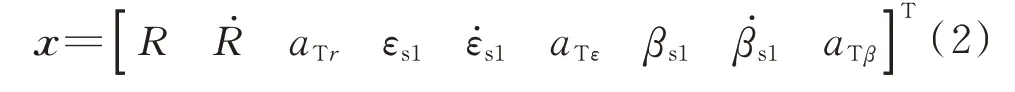
取控制向量为

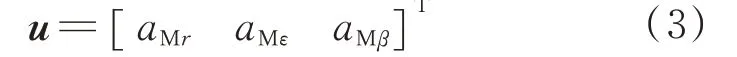
目标加加速度在弹上视线坐标系3 个轴上的投影可分别用函数far、faε、faβ表示，则状态方程可写为

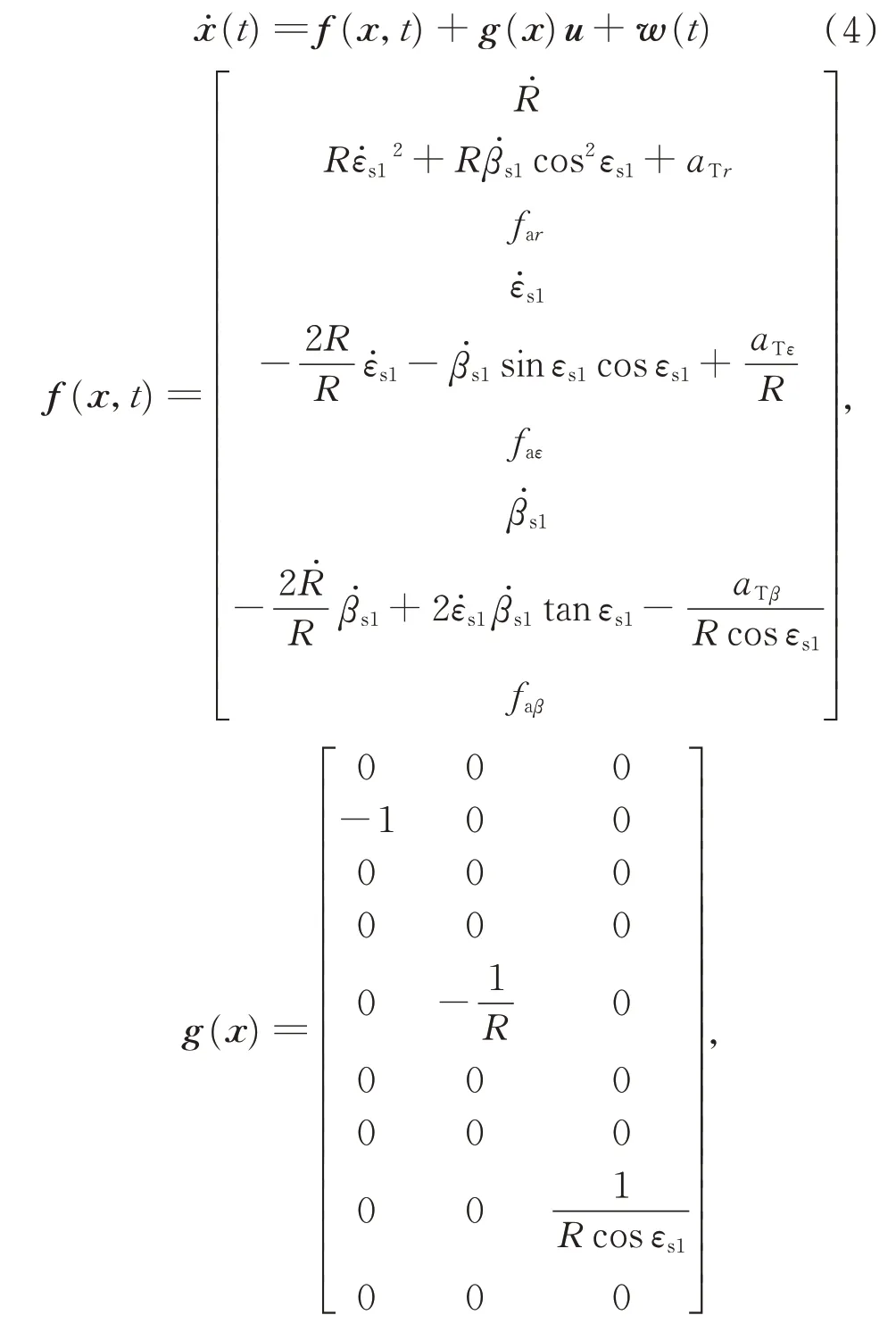
式中：w(t)为均值为零的白噪声向量。

对连续非线性状态方程进行离散、线性化。假设系统无输入，取采样时间为ΔT，将x(t+ΔT)在t进行泰勒展开，省略二阶以上的高阶项，可得

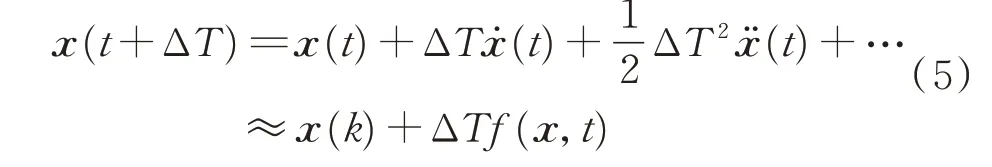
令t+ΔT≜k+1，t≜k，则有

对φ(k)线性化，可得

将Φ(k)记为状态转移矩阵，离散线性化状态方程为

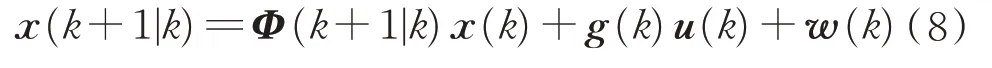
式中：w(k)为零均值的过程白噪声序列。

w(k)统计特性如下：

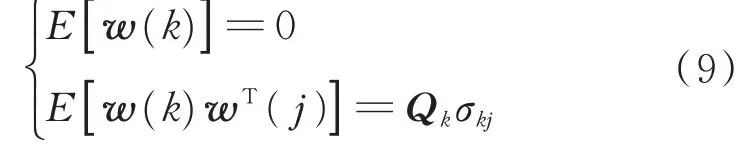
式中：Qk为系统噪声的误差方差阵；σkj为克罗尼克函数。σkj特性如下：

半主动式导引头可提供弹目相对距离变化率、视线角和视线角速率信息，因此，取观测向量为

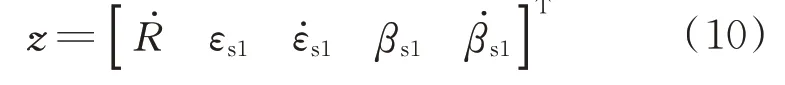
则离散形式的量测方程为

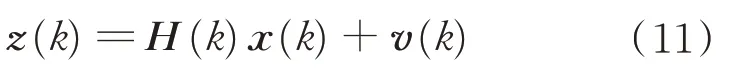
式中，

v(k)表示零均值的过程白噪声序列，其统计特性如下：

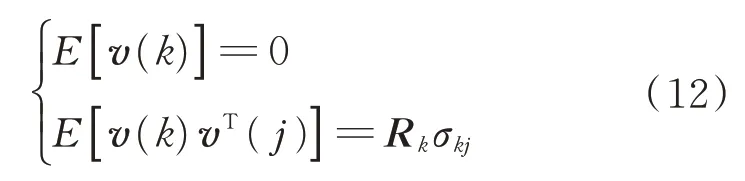
式中：Rk为噪声误差方差阵。

2 自适应加速度目标估计方法

2.1 交互多模型算法

蛇形机动目标具有机动性强、机动发生时刻不确定、机动持续时间不确定的特点。选用单一的目标运动形式不能准确描述蛇形目标的运动状态，因此，本文选用多个运动模型描述目标运动形式，基于IMM 算法实现目标加速度的估计。IMM 算法运用两个及以上的模型来描述目标运动形式，实时调整各目标运动模型的匹配概率，根据匹配概率对滤波结果进行加权融合，最终输出机动目标的状态估计。

本文选用Singer 模型和“当前”统计模型构建IMM 算法的模型集。Singer 模型认为目标的加速度可以用一阶时间相关过程描述，且加速度均值为零，可有效描述目标的加速度发生突变的情况。“当前”统计模型假设目标的加速度服从均值为“当前”时刻加速度的一阶时间相关过程，该模型认为下一时刻目标加速度取在“当前”时刻加速度的邻域内，可有效描述目标加速度连续变化的情况。该算法的流程如图1 所示。

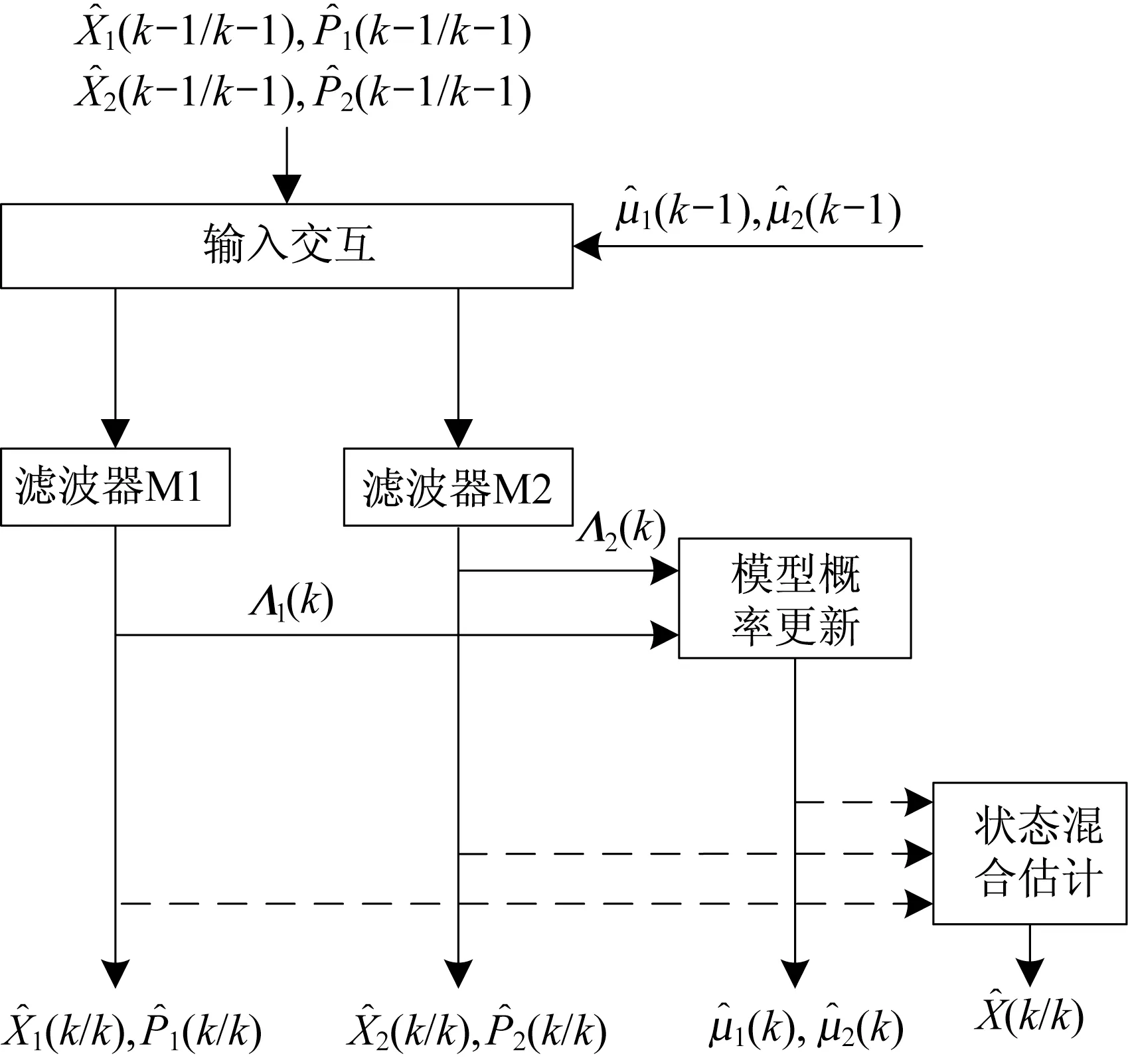
图1 交互多模型算法流程Fig.1 Flow chart of the IMM algorithm

在该算法中，采用Singer 模型的EKF 滤波器（M1）和采用“当前”统计模型的EKF 滤波器（M2）并行工作。交互多模型算法每次递推循环可分为4个步骤：1）将k−1 时刻得到的两个滤波器的模型概率μj(k−1)和状态估计值协方差阵作为输入进行计算，分别得到各模型的混合状态估计值和协方差 阵作为EKF 的初始条 件；2）根据k时刻得到的观测值进行EKF，得到k时刻各滤波器的状态估计值(k/k)、协方差阵(k/k)和观测残差Λj；3）根据Λj计算似然函数，更新滤波器的模型概率μj(k)；4）基于模型概率μj(k)，对个滤波器的状态估计值求和得到最终的估计结果(k/k)。IMM 算法每次循环递推的详细步骤见文献［12］。

2.2 加速度方差自适应算法

当目标运动模型为Singer 模型时，目标加加速度分量可描述为

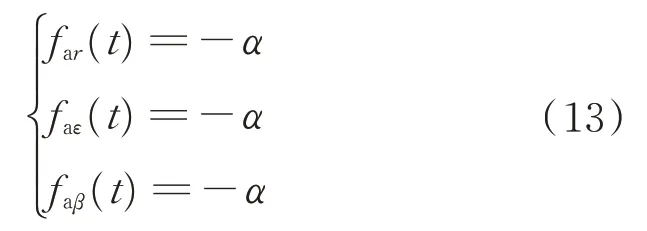
式中：α为目标的机动频率。

目标加速度方差为

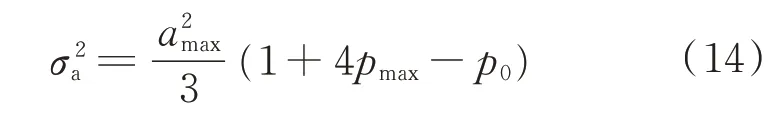
式中：amax为目标加速度最大值；pmax为目标机动加速度最大的概率值；p0为目标不机动的概率。

当目标运动模型为“当前”统计模型时，目标加加速度分量可描述为

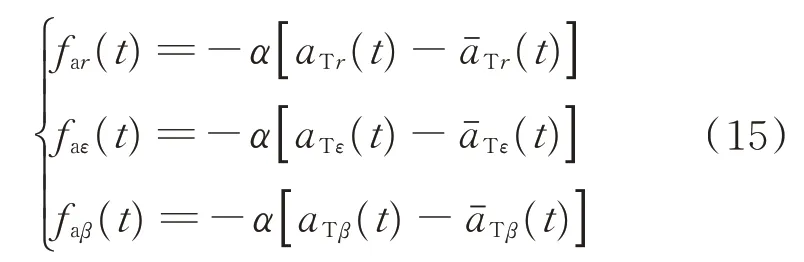
“当前”统计模型的加速度方差计算公式如下：

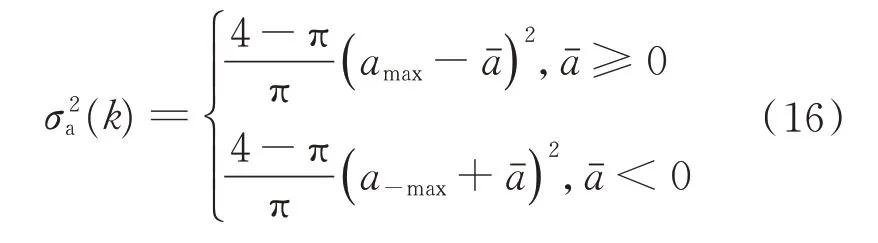
式中：a−max为目标的加速度最小值，通常为先验常值。

从式（15）和式（16）中可以看出：Singer 模型和“当前”统计模型的加速度方差的计算结果受预先设定的加速度最大值的影响。在实际应用中，目标的最大加速度通常是未知的。当目标实际加速度超出了预先设定的加速度最大值时，加速度估计精度就会下降。因此，本文基于预测残差对加速度方差的计算方法进行了改进。

在未获取量测值时，k时刻的目标最优速度预测值可由k−1 时刻的速度和加速度表示如下：

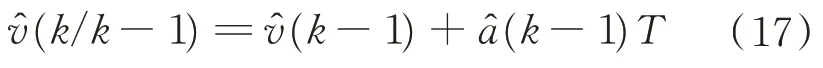
在得到量测值以后，经过残差修正的速度估计值为

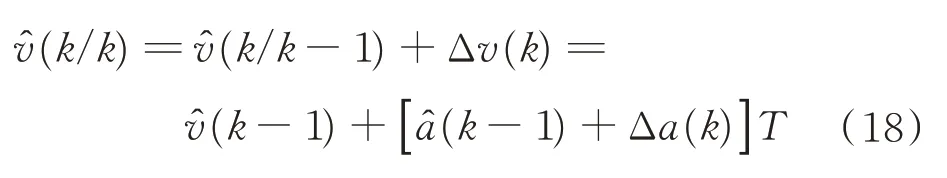
式中：Δa(k)表示k时刻的加速度变化量。通过修正，(k/k)相 较于(k/k−1)考虑了加 速度变 化量Δa(k)的影响，因此Δa(k)还可表示为

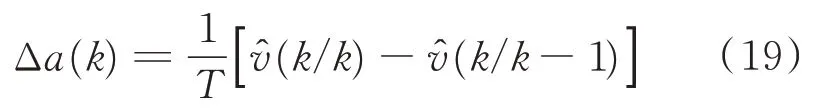
式（19）说明目标加速度变化量和速度预测值残差是线性相关，文献［13］研究表明目标加速度方差同加速度变化量的绝对值也是线性相关的，即

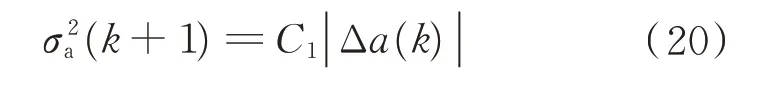
式中：C1为比例系数，取C1=1。

因此，可得k时刻目标加速度方差为

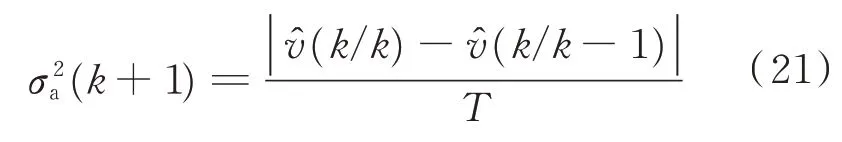
式中：C为比例系数。

本文的弹-目相对运动方程是建立在弹上视线坐标系下的，状态量不能直接描述目标加速度变化量。根据弹目相对速度vs与状态量之间关系，目标的加速度方差可表示为

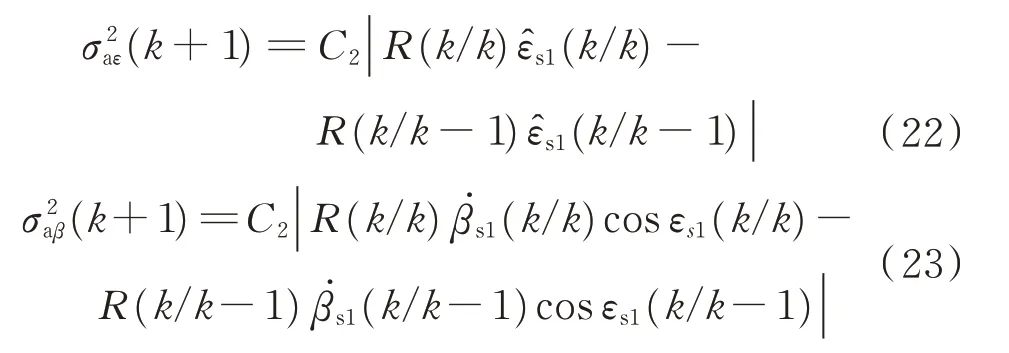
3 仿真分析

本文选用交互多模型算法和方差自适应的交互多模型算法，对水平蛇形机动目标的加速度进行估计。假设导弹保持静止状态，则滤波模型的控制向量为0，导弹的初始位置为XM0=[ 0 m 0 m 0 m]，初始速度为VM0=[ 0 m/s 0 m/s 0 m/s]。目标的初始位置为XT0=[ 40 000 m 10 m 2 000 m]，初始速度为VT0=[ 800 m/s 0 m/s 0 m/s]，运动周期为4 s，目标机动过载如下：

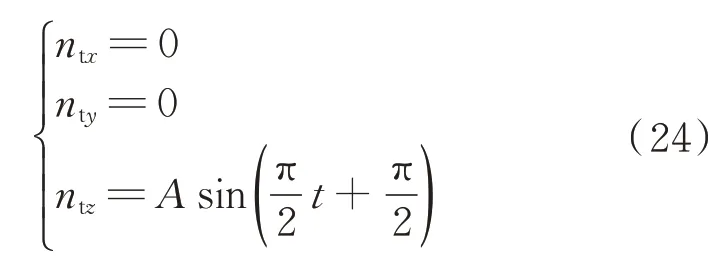
式中：ntx、nty、ntz分别为目标机动过载在地面坐标系3 个轴的分量；A为机动过载最大值。

本文将针对最大过载为10、15 和20 的蛇形机动目标进行仿真。对弹目视线角速率引入0.005 rad/s 的噪声，设定滤波模型中目标加速度最大值为150 m2/s。

图2～图4 分别为目标过载最大值为10、15 和20 的目标加速度估计曲线，图5～图7为经过50 次蒙特卡洛仿真得到的加速度均方根误差（RMSE）曲线。两种估计方法的加速度均方根误差均值见表1。

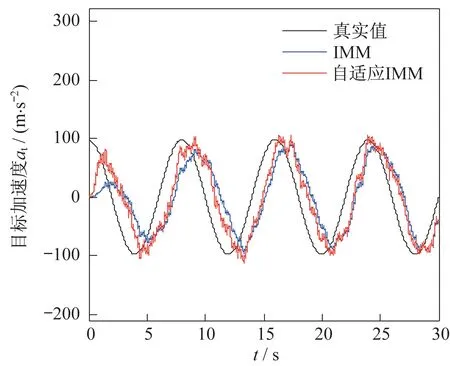
图2 过载最大值为10 时加速度估计曲线Fig.2 Estimated curves of the acceleration when the maximum overload is 10

图3 过载最大值为15 时加速度估计曲线Fig.3 Estimated curves of the acceleration when the maximum overload is 15

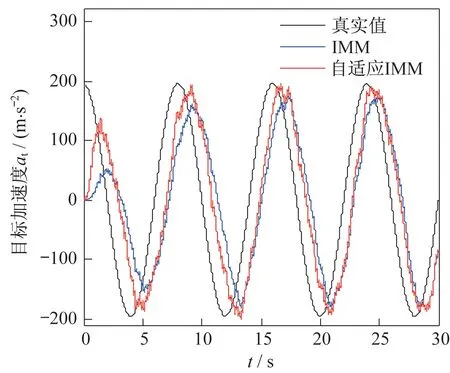
图4 过载最大值为20 时加速度估计曲线Fig.4 Estimated curves of the acceleration when the maximum overload is 20

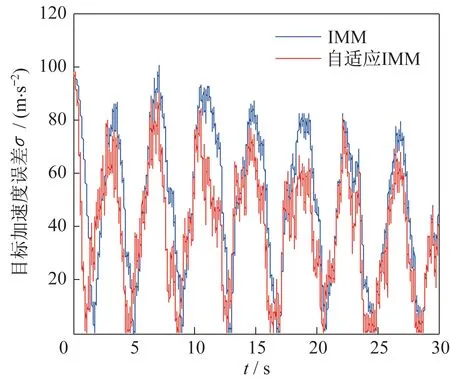
图5 过载最大值为10 时加速度均方误差Fig.5 RMSE curves of the acceleration when the maximum overload is 10

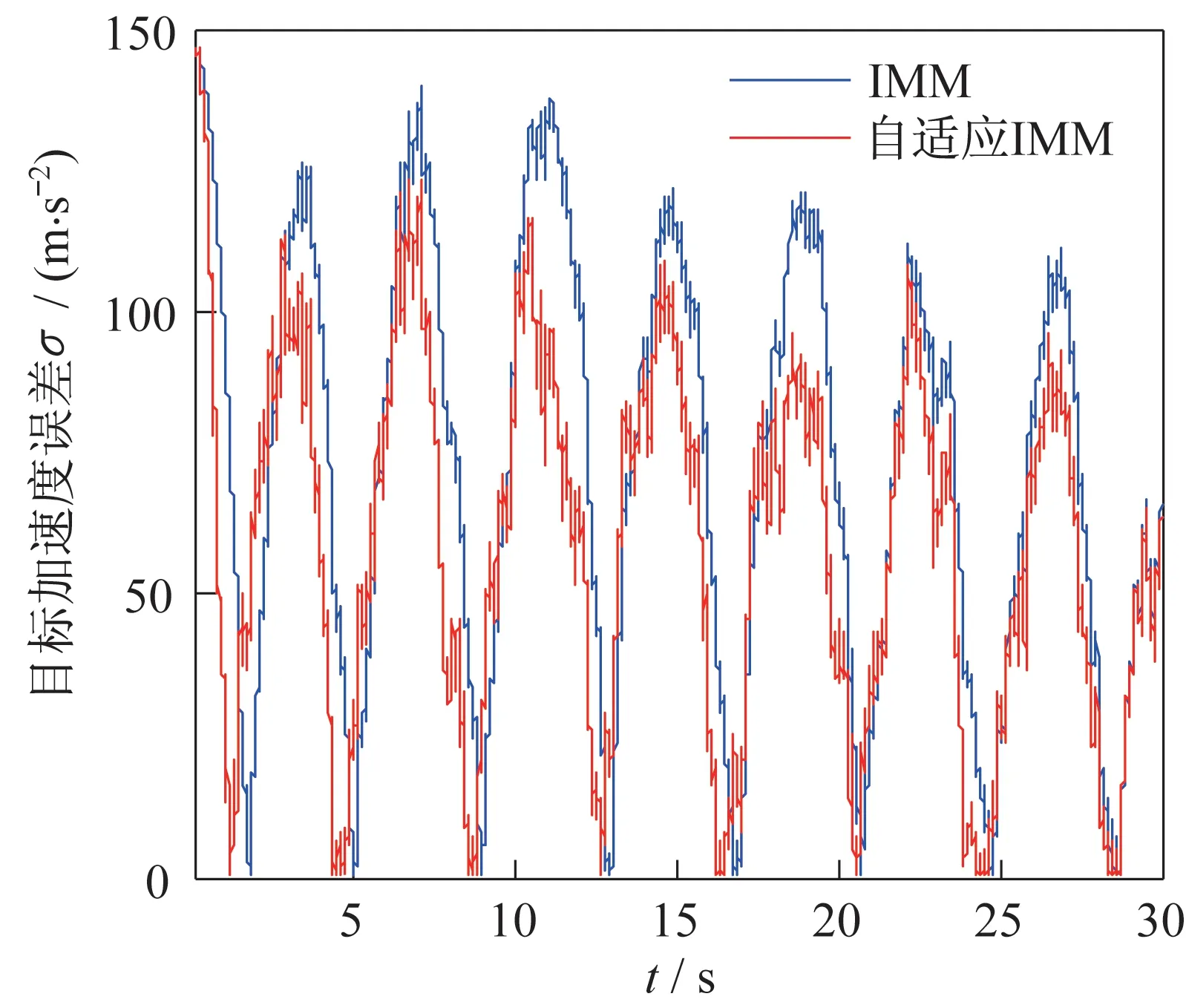
图6 过载最大值为15 时加速度均方根误差Fig.6 RMSE curves of the acceleration when the maximum overload is 15

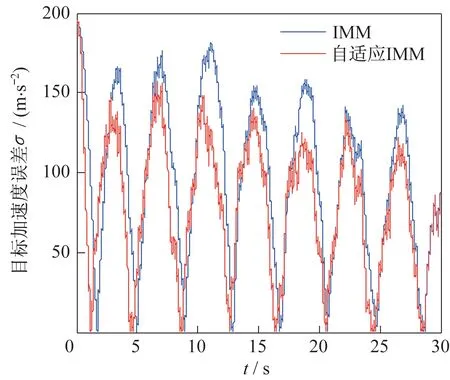
图7 过载最大值为20 时加速度均方根误差Fig.7 RMSE curves of the acceleration when the maximum overload is 20

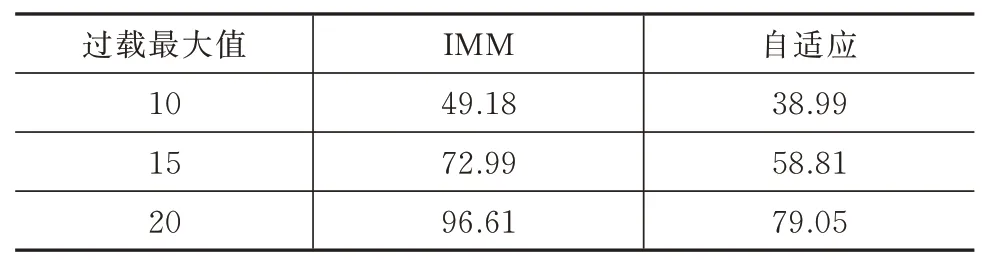
表1 两种算法的加速度均方根误差均值Tab.1 Average values of the acceleration RMSEs obtained from two algorithms m/s2

由图2～图4 可知：自适应IMM 算法的加速度估计方法的对三种不同过载的目标加速度估计结果更为良好，响应速度更为迅速。由图5～图7 可以看出，自适应IMM 算法的加速度估计结果均方根误差小于IMM 算法，随着目标机动过载的增加，IMM算法受限于预先设定的目标最大加速度值，估计误差大大增加。由图4 可知，当目标过载最大值达到20 的时候，IMM 算法估计加速度极大值约为16。表1 显示了自适应IMM 算法的加速度估计结果均方根误差均值小于IMM 算法。而本文通过改善目标加速度方差的计算方法，实现了对目标加速度方差的动态调整，提高了目标加速度的估计精度。

4 结束语

本文基于交互多模型算法建立了水平蛇形机动目标加速度的估计方法，针对Singer 模型和“当前”统计模型原有的加速度方差计算方法受限于预设加速度极值的缺陷，建立了新的加速度方差的计算方法，形成了蛇形机动目标加速度估计的自适应IMM 算法。通过仿真验证，该算法可有效提高目标的加速度估计精度，具有一定的工程应用价值，为遭遇点预测［14］和制导律的设计奠定了基础。