一种考虑摄动影响的星座构型稳定性设计方法

陈长春，林 滢，沈 鸣，戴光明，王茂才

（1.上海卫星工程研究所，上海 201109；2.中国长城工业集团有限公司，北京 100054；3.中国地质大学 计算机学院，湖北 武汉 430074）

0 引言

卫星星座在运行过程中，受到地球非球形摄动、太阳光压和大气阻力等摄动力的影响，会慢慢偏移其标称轨道，进而使星座整体构型被破坏，星座性能降低，影响到卫星星座稳定性［1］。

Walker 星座由于其独特的构型，在通讯、定位、海洋、军事等领域起到了至关重要的作用［2］。随着工程需求的提高，对Walker 星座的精确度要求不断提高，研究考虑各种摄动模型后的精确Walker 星座发射以及Walker 星座在长期工作运行中如何进行星座稳定性设计，从而保证星座构型稳定性，已成为研究热点［3］。

在对Walker 星座构型稳定性方案进行分析时，需对各种摄动模型进行精确建模，分析不同摄动力对卫星轨道的影响［4-5］。考虑摄动模型下，在一个典型的Walker 星座进行部署时，由于星座中各颗卫星发射时间的区别，其所受的摄动力的时间累积效应也有所差别［6］，因此，需要消除在该累积效应带来的影响量［7］。在建立标准Walker 星座后，结合Walker星座构型特性，分析其卫星轨道在摄动模型下产生的运动轨迹变化趋势［8-9］，研究设计星座构型保持策略，以实现保持星座构型稳定性的目的［10］。

1 设计思路

根据Walker构型整体对称的特性［11］，若对星座中所有卫星的纬度幅角和升交点赤经都改变ΔΩ与Δλ，星座的整体构型将不会受到影响，仍然会保持稳定。

编号为i的卫星在考虑各种摄动下的轨道命名为Si，在t时刻其升交点赤经和纬度幅角分别命名为Ωi(t)和λi(t)，其标称轨道命名为，在t时刻标称轨道升交点赤经和纬度幅角分别命名为(t)和(t)，则在t时刻，Si与的升交点赤经和纬度幅角之差为

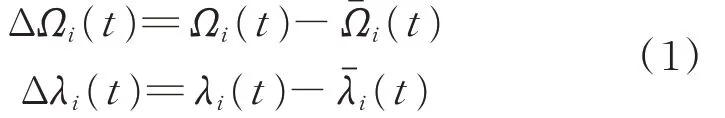
由式（1）计算得到的偏差称为实际轨道与标称轨道的绝对偏移量。

在t时刻整个星座的升交点赤经之差与纬度幅角之差被定义为星座中所有卫星升交点赤经差和纬度幅角差的平均值，即

式中：N为星座中卫星的总数目。

由式（2）得到的结果称为实际星座与标称星座的平均偏移量，记

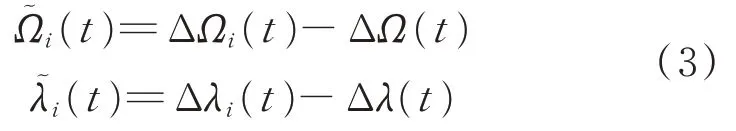
为每颗卫星的独立偏移量。

根据式（3），可以计算得到每个时刻的升交点赤经和平均纬度幅角的独立偏差为以及

根据每颗卫星的独立偏差分别对轨道参数进行调整，若调整后其短周期项波动范围在允许最大偏移量范围内，则卫星在轨期间不需要再进行调整即满足任务要求，否则需要在轨调整。

2 星座构型稳定性设计方法

2.1 半长轴影响分析

根据星座保持原理，进行轨道修正。为了与文献［12］中的数据进行对比分析与验证，所有参数选取与文献中的数据相同，具体参数见表1。缩水，摄动模型只考虑非球形模型，且先对第一颗卫星进行分析。

表1 MEO 卫星星座构型Tab.1 Configuration of the MEO satellite constellation

通过实验发现：采用CSTK 和STK 数值所计算的Ω1的线性项与理论公式中的Ω1的值整体斜率吻合，如图1 所示；但采用CSTK 和STK 数值所计算的λ1的线性项与理论公式中的λ1的值整体斜率无法重合，如图2 所示。图中，横坐标为MJD2K 时间历元，即从2000年1 月1 日00∶00∶00 起算的时间历元，时间增加1 d，MJD2K 的数字增大1，纵轴为角度偏移量。

图1 升交点赤经偏移量（1 个月）Fig.1 The offset of the right-ascension-of-ascending-node（one month）

图2 相位角偏移量（1 个月）Fig.2 The offset of the phase angle（one month）

实验中，CSTK 和STK 数值所计算的λ1的线性项与理论公式中的λ1的值整体斜率无法重合，而在使用影响矩阵A获得需要调整的轨道半长轴和轨道倾角时需要用到理论λ1的值，因而结果会出问题。经过实验与分析得知，产生这个问题的原因在于半长轴的短周期项的影响。实验中，STK 非球形摄动模型下半长轴偏移量随时间变化如图3 所示。

图3 非球形摄动下半长轴偏移量Fig.3 The offset of the semi-major axis under nonspherical perturbation

从图3中看到卫星的半长轴是随时间变化的，需要考虑半长轴长期项的影响为

式中：Re为地球半径，其数值取6 378.137；a、e、i、ω与f分别为卫星的半长轴、偏心率、轨道倾角、近地点俯角和真近点角；r为卫星到地心的距离；J2为地球的非球形效应的二阶带谐项系数。

根据实际问题，简化后为

因而第一颗卫星的半长轴长期项影响计算为1.590 010 114 820 334 1，将实验数据带入STK 重新进行计算分析，结果如图4 所示。考虑到半长轴长期项的影响后，STK 数值所计算的λ1的线性项与理论公式中的λ1的值整体斜率相互吻合。

2.2 卫星星座稳定性构型设计流程

图4 由实验数据获得的相位角偏移量（1 个月）Fig.4 The offset of the phase angle obtained with the experimental data（one month）

通过实验分析，在消除卫星轨道因轨道半长轴短周期项的影响后，考虑多种摄动因素下，采用卫星星座整体偏移和数据拟合思想来设计星座构型稳定性保持策略，具体步骤如下：

步骤1消除星座卫星轨道因轨道半长轴短周期项的影响；

步骤2计算同时带3 种摄动模型的星座中各颗卫星的升交点赤经绝对偏移量和相位角绝对偏移量；

步骤3根据卫星星座整体偏移原理，计算出每颗卫星的独立偏移量；

步骤4对卫星星座中各颗卫星的独立偏移量进行数据拟合，并根据参数偏置摄动补偿原理计算出各颗卫星需要调整的半长轴的主动偏置量Δa和轨道倾角主动偏置量Δi；

步骤5对偏置后的卫星星座进行仿真测试，判断是否已完全消除摄动对其产生的长期影响，以达到保持星座构型稳定性的目的，若还没有消除，则转步骤4，否则转步骤6；

步骤6结束。

3 仿真试验及结果分析

3.1 卫星参数

由于考虑到不同轨道高度摄动因素对卫星轨道的影响不同，特别是轨道高度的影响，为了验证调整方案同样适用于其他类型Walker 星座，实验选取了一组中轨道高度的卫星数据进行实验测试，具体参数见表2。

表2 卫星星座参数Tab.2 The parameters of the satellite constellation

3.2 测试结果及分析

首先获得星座40 颗卫星的所有偏移量，考虑到前面提到的轨道半长轴的长期项，计算出各颗卫星开始前轨道半长轴的长期项影响量，消除其半长轴长期项的影响；然后再计算出每一时刻星座的平均偏移量，对其进行拟合，由于每颗卫星偏移量较大，拟合只选取具有代表特征的前45 d 的数据进行拟合。

通过前45 d 的数据进行拟合修正后，得到的修正后的星座，相位角和升交点赤经偏移量随时间的变化曲线分别如图5 和图6 所示。

图5 40 颗卫星各自相位角独立偏移量Fig.5 The independent offsets of the phase angles of 40 satellites

图6 40 颗卫星各自升交点赤经独立偏移量Fig.6 The independent offsets of the right-ascension-ofascending-nodes of 40 satellites

由图5 可知：40 颗卫星的相位角仍然存在一个较大的随时间增加的一个线性项，在2年时间内，最大相位角偏移量约为63°。

如图6 所示，通过星座整体偏移，基本上已经消除了升交点赤经偏移量的线性项影响，但部分卫星仍然存在一个非常微小的线性项。

以上可知，摄动因素在2年内对卫星轨道的升交点赤经和相位角产生非常大的影响，使星座整体结构变形，若对其不进行星座控制保持策略，在短时间内即会超过星座的最大容许偏移量，使星座构型整体失效，不能达到预期的目的。

图5 和图6中的结果形成的原因，主要是升交点赤经偏移量和相位角偏移量由于摄动因素存在长期项外，还存在短周期项，在数据拟合过程中，可能无法通过一次数据拟合就十分准确表示其偏移量的变化量，因而需要进行第二次拟合调整。

将第二次修正调整后的轨道参数重新代入STK中进行计算检验，计算数据经过转换后实际偏差量如图7 和图8 所示。

图7 二次修正后40 颗卫星相位角偏移量Fig.7 The offsets of the phase angles of 40 satellites after the secondary correction

图8 二次修正后40 颗卫星升交点赤经偏移量Fig.8 The offsets of the right-ascension-of-ascendingnodes of 40 satellites after the secondary correction

由图7 和图8 可知：40 颗卫星的相位角和升交点赤经偏移量在2年时间内，最大偏差都非常小，相位角的偏差不超过0.25°，升交点赤经的偏差不超过0.20°，而且两者均不存在线性项效应。

通过计算可知，该星座对应的最大容许相位角偏移量为1°，最大容许升交点赤经偏移量也为1°，则该Walker 星座的偏差在最大容许偏差范围之内。因此，可以得到结论：在考虑各种形式的摄动力效应下，该Walker 星座在2年时间内构型是稳定的。该数值仿真实验也表明了数据拟合方法能有效地消除摄动对卫星轨道长期项影响，仅通过调整后的卫星轨道能在较长时间内保持其整体稳定性，达到了星座构型保持的目的。

4 结束语

本文对星座构型的最大容许偏移量进行分析计算，以此作为星座构型稳定性策略是否有效的衡量标准。在对卫星星座受到的摄动模型建模后，通过对摄动模型对卫星轨道的影响的深入分析实验，提出了采用曲线拟合中的最小二乘法来分析和调整卫星初始轨道，并提出了星座整体偏移方法，结合卫星参数初始轨道偏置补偿原理来获得保持星座构型稳定性的目的。在设计了对应的星座构型稳定性策略后，对于所需要进行的卫星轨道的调整量，根据调整所需要的能量，从节省能源的角度出发，采用脉冲调整的方案进行机动变轨。最后通过实验验证了整套设计方案的可行性和高效性。