含裂纹容器的有限元分析

韦权权 王政威 杨溪荣 罗惠敏

摘      要：利用有限元通用软件ANSYS Workbench，建立容器的有限弹性体三维有限元模型，进行地震工况下不同裂纹长度、不同裂纹方向、不同支腿数量和不同容器高度下的应力分析，得到断裂力学中表征裂纹尖端附近应力场，进而得出以下结论：裂纹长轴长度和角度的变化对应力场影响;等效应力值随着裂纹长轴长度的变大显著变大，等效应力最大点随着裂纹长轴长度的变大由长轴边缘移到短轴边缘;等效应力值随着裂纹长轴角度的变大而变化，在22.5°时达到最大;等效应力最大点随着裂纹长轴角度的变大，由长轴边缘移到短轴边缘。

关  键  词：裂纹;有限元;容器;分析

中图分类号：TQ 052       文献标识码： A       文章编号： 1671-0460（2019）08-1885-04

Abstract： Using ANSYS Workbench， a finite elastomer three-dimensional finite element model of the container was established. Stress analysis under different crack lengths， different crack directions， different number of legs and different height of the container was carried out under seismic conditions. The stress field near the crack tip was characterized in fracture mechanics， and the following conclusions were drawn： the change of the length and angle of the long axis of the crack affects the stress field; the equivalent stress value increases significantly with the increasing of the length of the long axis of the crack， and the maximum point of the equivalent stress moves from the edge of the long axis to the edge of the short axis with the increasing of the length of the long axis of the crack; the equivalent stress value changes with the increasing of the angle of the long axis of the crack， reaching its maximum at 22.5 degrees; the maximum point of equivalent stress moves from the edge of the long axis to the edge of the short axis with the increasing of the angle of the long axis of the crack.Key words： Crack; Finite element; Vessel; Analysis

在對炼油和化工装置的运行与定期检验中，常会发现部分容器存在裂纹缺陷。如果一旦发现容器的裂纹缺陷就立即停产检修或者报废处理，那么会存在不合理和不经济性。尤其是在储存大量危险介质的含裂纹储罐，其危险性大、波及面广;若其存在裂纹缺陷，我们如果能对缺陷的发展及可能造成的危险做出判断，那么我们就可以最大限度的发挥储罐的经济效益而不会发生危险。因此，工程界一直在努力寻找这种安全评定的准则。

在工程应用中，由于容器的实际结构通常都是有限弹性的，因此研究有限弹性的表面裂纹结构与实际相符更有研究意义。对于有限弹性体三维表面裂纹问题，目前国内外学者大都通过数值分析方法求出的。鉴于前人的经验本文采用有限弹性体计算应力强度因子。

1  有限元模型建立

考虑到本文主要考察裂纹，所以建模时忽略接管和部分小结构。由于考虑的裂纹位于储罐筒体中部，忽略其他结构不会影响裂纹的考察。壳体采用实体单元建模，支腿采用梁单元建模，梁单元与实体单元之间采用MPC绑定。

本储罐结构及载荷形式复杂，所以本文选取全模型进行计算模拟。本文采用大型通用有限元软件ANSYS WORKBENCH自带的建模工具DesignModeler建立三维实体模型，为了模拟裂纹应力场、应变场以及应力强度因子，在建模时裂纹前沿采用退化的二十节点等参元，其他部位采用二十节点等参元，这样既能求出裂纹前沿的应力奇异场又能满足很好的精度[1-5]。

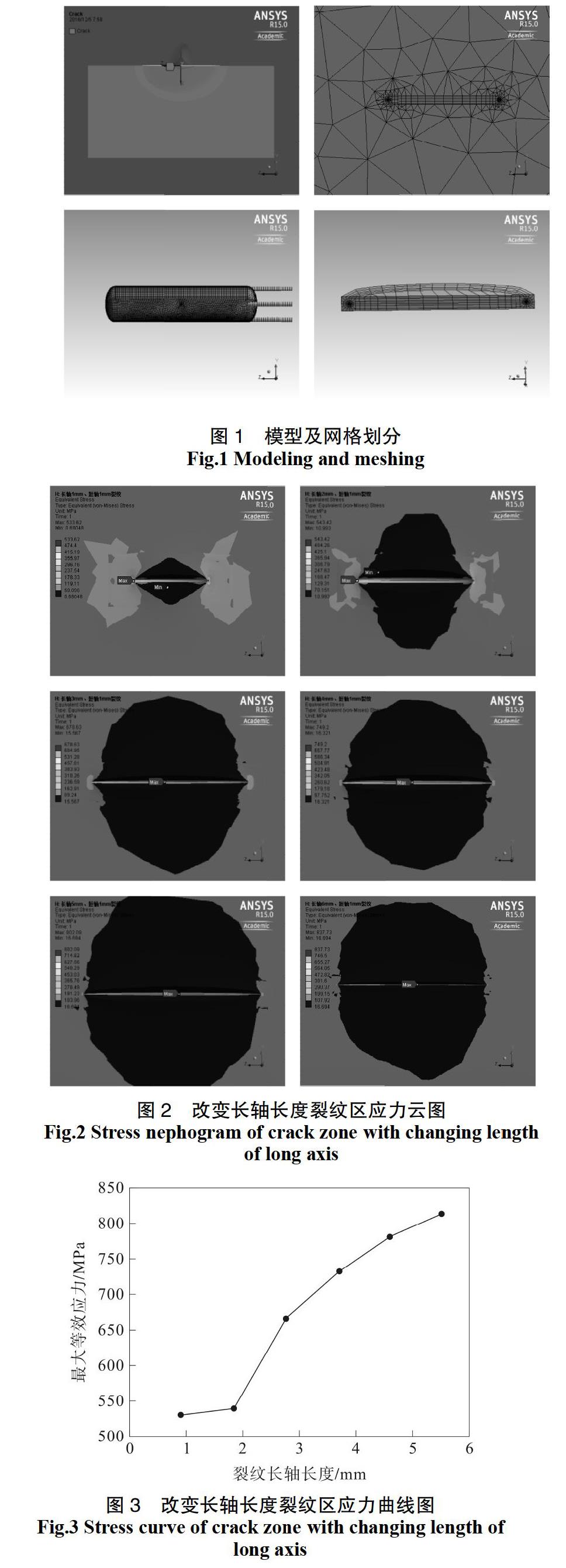
由于本文分析储罐结构的全模型，因此在其内壁处施加压力载荷，在整体上施加地震载荷，在支腿底部施加全约束。由于本文裂纹处载荷工况的复杂性，在其裂纹处将产生复合型裂纹形式。在裂纹的建模过程中，建立椭圆形表面裂纹，为控制裂纹处的网格密度，本文在网格裂纹处沿裂纹宽度方向划分8条轮廓网格，以便为后续考察8条轮廓路径上的应力强度因子做准备。模型及网格划分见图1。

2  含裂纹容器的应力分析

2.1  裂纹长轴尺寸对应力场的影响

为了进一步分析轴向裂纹长轴（裂纹长轴方向垂直于储罐筒体环向应力方向）方向尺寸变化（裂纹短轴尺寸不变）对有限弹性体中表面裂纹应力场的影响及其规律性，我们选取裂纹短轴直径为1 mm，长轴直径分别为1、2、3、4、5、6 mm的6种椭圆表面裂纹形式进行分析。

由图2可以看出随着裂纹长轴长度的变大，等效应力值也显著变大，等效应力最大点的位置随着裂纹长轴长度的变大，由长轴边缘移到短轴边缘。由此说明，当裂纹长轴长度较短时，其主要沿裂纹长轴方向扩展;当裂纹长轴长度较长时，其主要沿裂纹短轴方向扩展。

由图3可以看出裂纹长轴长度小于2 mm时，等效应力增长缓慢;裂纹长轴长度在2～4 mm时，等效应力值增长迅速;当裂纹长轴长度大于4 mm后，等效应力增长又变缓慢。

2.2  裂纹长轴角度对应力场的影响

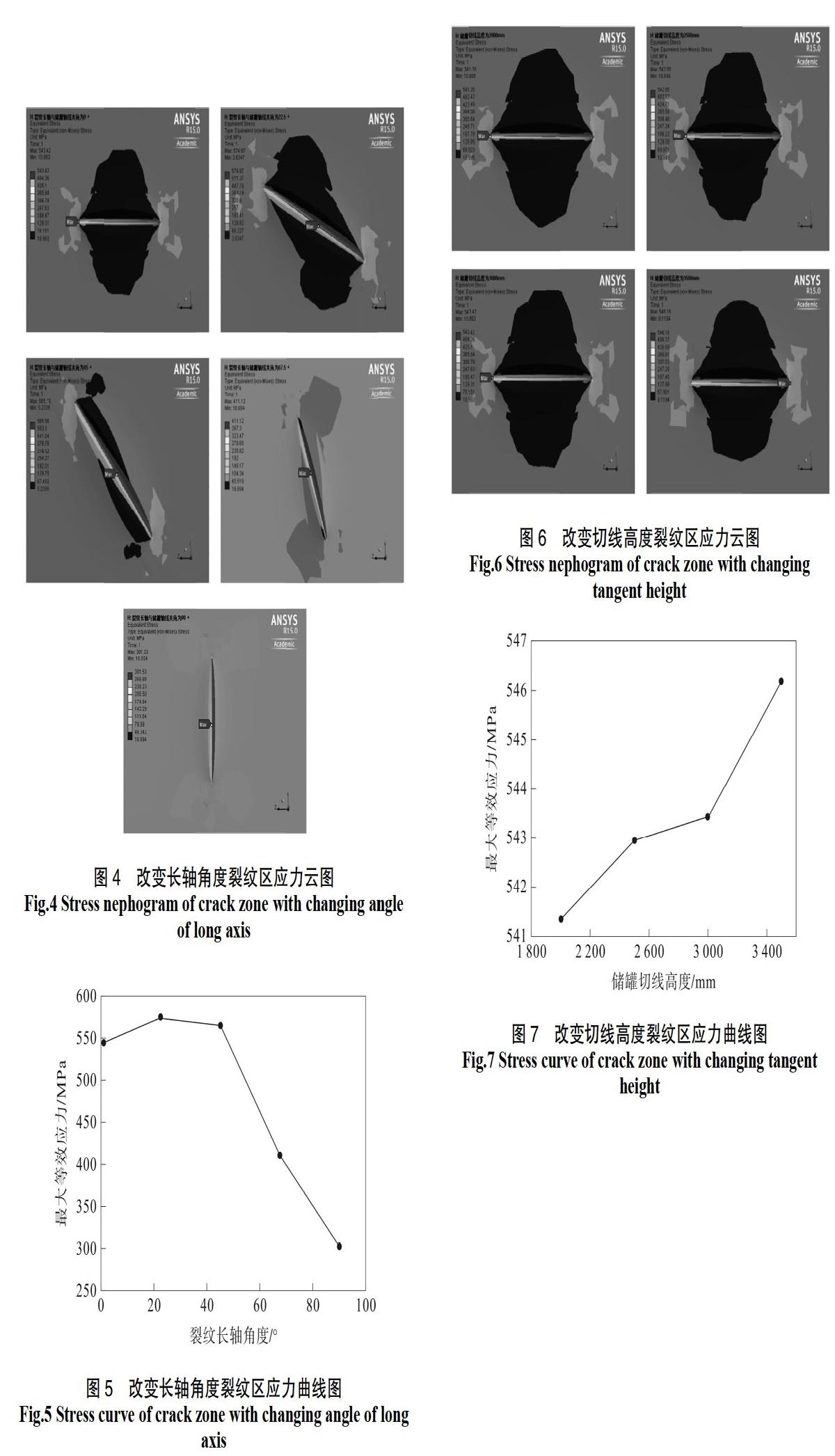
为了进一步分析轴向裂纹长轴（裂纹长轴方向垂直于储罐筒体环向应力方向）方向角度变化（裂纹长轴直径2 mm、短轴直径1 mm）对有限弹性体中表面裂纹应力场的影响及其规律性，我们选取裂纹长轴与储罐轴线夹角分别为0°、22.5°、45°、67.5°、90°的五种椭圆表面裂纹形式进行分析。

由图4可以看出随着裂纹长轴角度的变大，等效应力最大点随着裂纹长轴角度的变大，由长轴边缘位置移到裂纹短轴边缘位置。由此说明，当裂纹长轴角度较小时，其主要沿长轴方向扩展，当裂纹长轴角度较大时，其主要沿短轴方向扩展。

由图5可以，看出裂纹长轴角度小于22.5°时，等效应力缓慢增长;裂纹长轴角度大于22.5°时，等效应力值下降;在22.5°～45°之间，等效应力值缓慢下降;超过45°时，等效应值迅速下降。此种现象是因为裂纹张开方向受力由环向应力逐渐变为轴向应力，张开方向應力值逐渐变小导致的。

2.3  切线高度对裂纹应力场的影响

为了进一步分析储罐切线高度对有限弹性体中表面裂纹（裂纹长轴直径2 mm、短轴直径1 mm）应力场的影响及其规律性，我们选取储罐切线高度分别为2 000、2 500、3 000、3 500 mm四种储罐中心位置椭圆表面裂纹形式进行分析。

由图6、图7可以看出随着储罐切线高度的变大，等效应力最大值随着储罐切线高度的增加而缓慢增加，等效应力最大点的位置不变。由此说明，储罐切线高度的增大，其由于承受地震载荷产生的弯矩作用而使轴向应力增大，从而影响裂纹等效应力最大值。

2.4  支腿数量对裂纹应力场的影响

为了进一步分析储罐支腿数量对有限弹性体中表面裂纹（裂纹长轴直径2 mm、短轴直径1 mm）应力场的影响及其规律性，我们选取储罐支腿数量分别为3、4的两种储罐中心位置椭圆表面裂纹形式进行分析。

由图8可以看出随着储罐支腿数量的增多，等效应力最大值基本没有变化，等效应力最大点的位置不变。由此说明，储罐支腿数量的多少，对于其远离支腿部位的局部应力没有影响，根据应力衰减观点，在支腿数量变化的时候，只影响支腿部位局部的应力状况， 对于远离支腿部位的地方没有影响。

3  结 论

通过对裂纹在多种情况下应力场的分析，可以得出以下结论：

（1）裂纹长轴长度和角度的变化对应力场影响显著，其余因素对应力场影响不明显。

（2）随着裂纹长轴长度的变大，等效应力值也显著变大，等效应力最大点随着裂纹长轴长度的变大，由长轴边缘位置移到裂纹短轴边缘位置。

（3）随着裂纹长轴角度的变大，等效应力最大点随着裂纹长轴角度的变大，由长轴边缘位置移到裂纹短轴边缘位置，裂纹长轴角度小于22.5°时，等效应力缓慢增长;裂纹长轴角度大于22.5°时，等效应力值下降;在22.5°～45°之间，等效应力值缓慢下降;超过45°时，等效应值迅速下降。

参考文献：

[1]Kim Y， Kim J， Ahn J， et al. Effects of local wall thinning on plastic limit loads of elbows using geometrically linear FE limit analyses[J]. Engineering Fracture Mechanics， 2008， 75： 2225-2245.

[2]Raju， IS. Calculation of Strain Energy Release Rate with higher order and singular finite element[J]. Engineering Fracture Mechanics， 1987， 28：251-274.

[3]解德. 断裂力学中的数值计算方法及工程应用[M]. 北京：科学出版社，2009 ：9-20.

[4]郑耀辉，崔林琳.压力容器边缘应力的有限元分析[J].沈阳航空工业学院学报，2001，18（3）：12-16.

[5]祁建磊，路智敏.含裂纹压力容器的安全评定及强度因子求解[J].化工设备与管道，2016，53（3）：15-27+84.