基于无迹卡尔曼滤波的空间目标双星定位方法

张 宇，夏鲁瑞，蔡博宇

（1.中国人民解放军63757 部队，黑龙江 佳木斯 154002；2.航天工程大学 太空安全研究中心，北京 101416）

0 引言

在对空间目标进行探测定位的过程中，地基探测系统对其探测时间短、定位精度不高，而天基探测系统在太空中不受国界限制，探测范围大、定位精度高。但是，天基探测系统是基于几何法的双星定位，误差较大，本文研究了基于动力学滤波方法的双星定位方法，并比较了不同滤波方法对空间目标的定位精度。

自由段目标跟踪的经典方法是扩展卡尔曼滤波［1-5］，由于该方法的基本原理是将观测方程进行线性化，因此，在非线性较强、数据量少的情况下容易出现滤波发散。无迹卡尔曼滤波［6-11］和粒子滤波［12-13］等因基于采样的非线性估计算法而得到广泛关注。粒子滤波能够解决扩展卡尔曼滤波所存在的问题，但其运算效率和粒子退化问题尚未得到解决［13］。无迹卡尔曼滤波运算效率较高，通过计算求解sigma 点，避免了求解Jacobian 阵，同时也能避免粒子滤波的粒子退化，近年来在弹道估计领域受到很大程度的关注［10-11］。为了进一步提高非线性估计的精度，高阶无迹卡尔曼滤波［14］、迭代扩展卡尔曼滤波［15］等方法也涌现出来。叶飚等［16］利用双星交汇几何定位以及一种基于扩展卡尔曼滤波的目标自由段弹道估计的方法，对目标进行了定位跟踪，并给出了误差计算模型，主要解决了从多星中选择最优星对目标进行定位的问题。秦雷等［17］为了更好地满足机动式弹道滤波的需要，通过双站红外跟踪方法与卡尔曼滤波算法相结合，得到了斜距估计误差和斜距估计相对误差，实现对临近空间目标飞行器跟踪，并保证了定位跟踪精度在允许范围之内，对目标进行定位的双站是地面双站，并不是空间双星，模型建立上有所不同。

本文在空间目标的观测方程建立过程中，以双星对空间目标的单位观测矢量为观测量，且观测数据的获得考虑了高精度轨道外推模型和大气阻力摄动模型，并利用无偏量测转换方式，有效避免了系统的非线性换变换所带来的噪声协方差估计不准确的问题。通过比较两种滤波方法在相同条件下对目标的定位误差，可知无迹卡尔曼滤波方法在收敛速度和定位精度上均优于扩展卡尔曼滤波方法。

1 双星对目标探测定位模型

假设空间目标T绕地球自由飞行，当卫星1 和卫星2 同时对空间目标可见时，对其进行观测并测角，得到在卫星本体坐标系内对空间目标T的方位角α1、α2和高低角β1、β2。双星对空间目标观测模型如图1 所示。

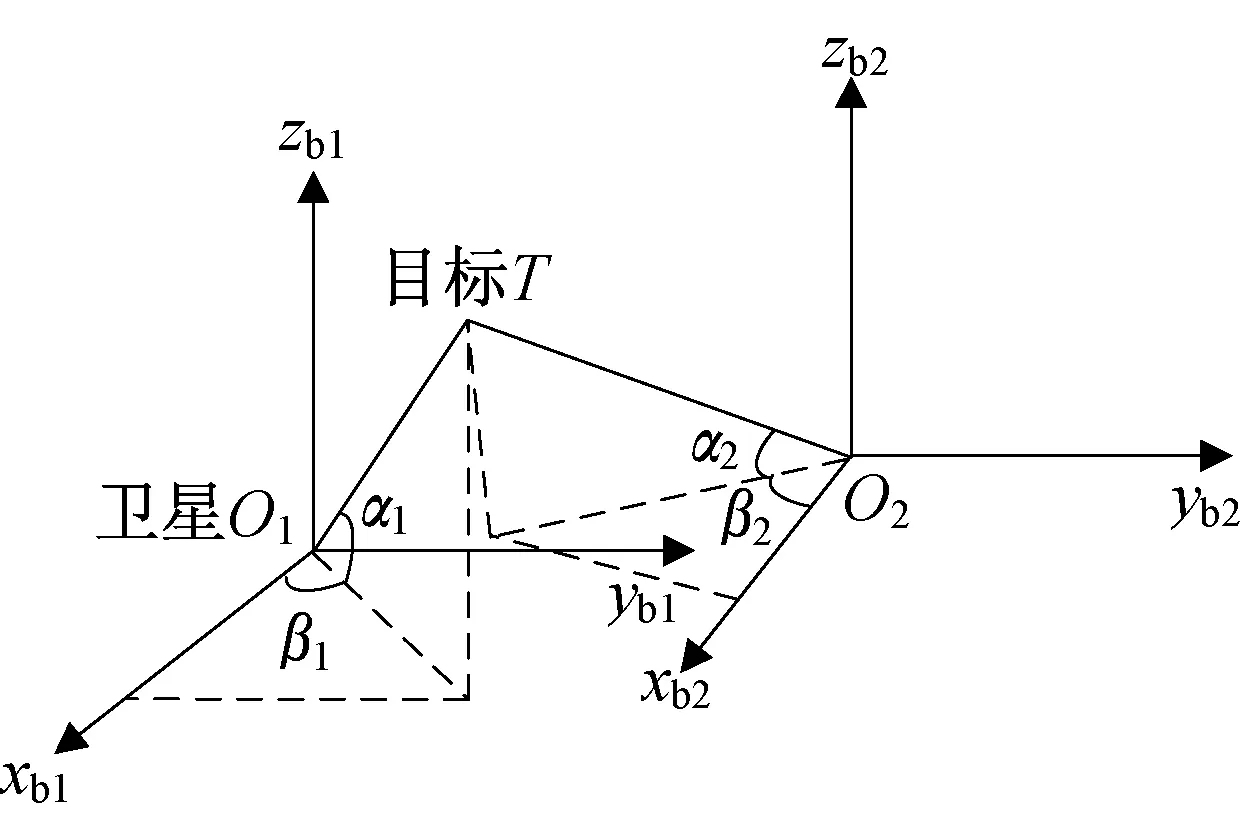
图1 双星对空间目标观测模型Fig.1 The observation model of two satellites on a spatial target

1.1 动力学模型

空间目标T的动力学状态变量X定义为在J2000.0 坐标系下的位置矢量r与速度矢量v，即

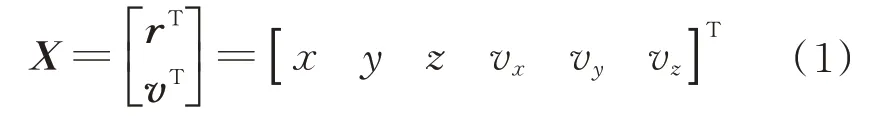
根据牛顿动力学方程，空间目标T的动力学模型可以表示为

式中：aC为地球引力加速度；aE为地球非球形摄动加速度；aS为太阳引力加速度；aM为月球引力摄动加速度；aSRP为太阳光压摄动加速度；aDRAG为大气阻力摄动加速度；aTHRUST为机动控制加速度。

为了简化计算，本文动力学模型中加速度项只考虑地球引力aC和地球非球形引力摄动J2 项摄动力aE，即

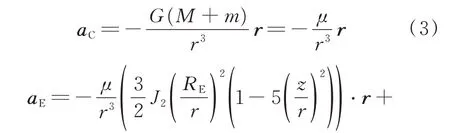
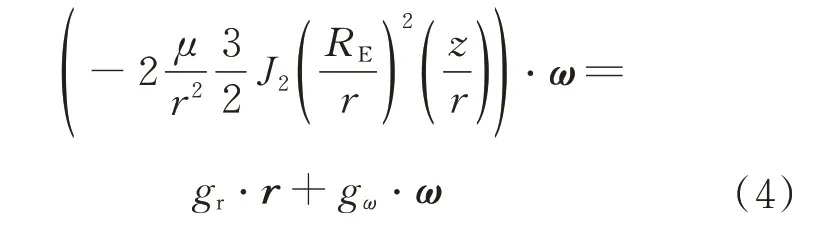
式中：μ为地球引力常数；RE为地球赤道半径；J2=1.082 63×10−3为二阶带谐项系数，且

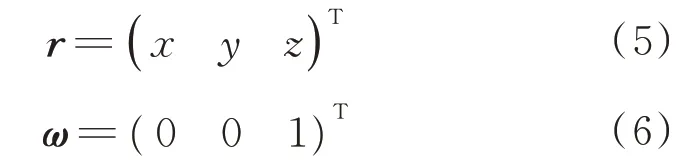
因此，空间目标T 的动力学模型方程为

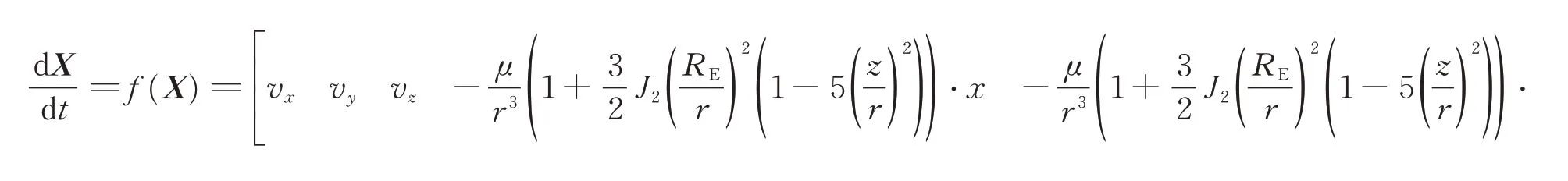
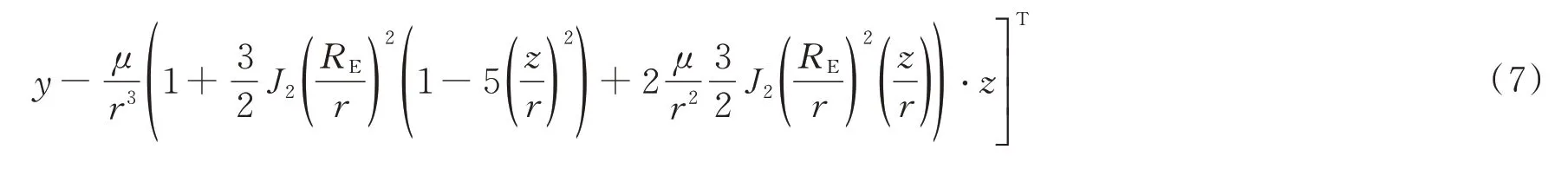
1.2 系统观测方程

双星的量测矢量由方位角α和高低角β组成。

通常情况下，测量值在卫星本体坐标系中的投影矢量表示为

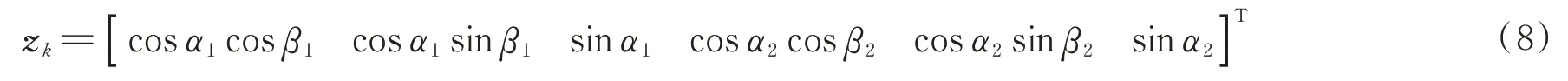
容易看出，测量值为双星到目标连线的单位矢量为

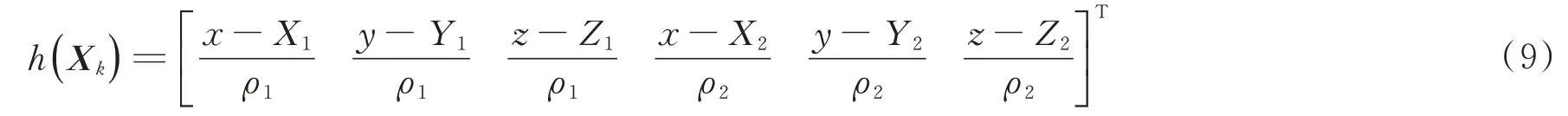
式中：

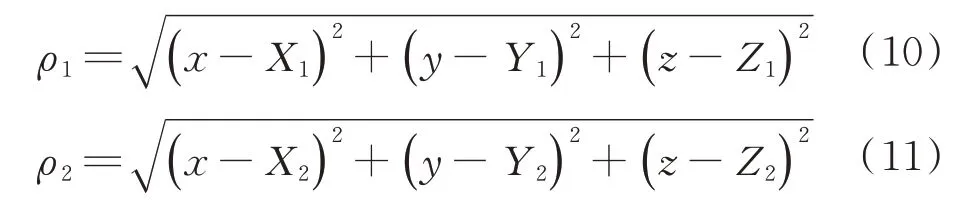
其中，［x，y，z］T为空间目标在J2000.0 坐标系下的位置矢量，［X1，Y1，Z1］T和［X2，Y2，Z2］T为双星的位置矢量。要使zk=h（Xk），必须将两者统一到同一坐标系系统中。

根据坐标转换，J2000.0 坐标系到卫星本体坐标系的转换矩阵M为

式中：GI为J2000.0 坐标系到轨道坐标系的转移矩阵；BG为卫星轨道坐标系到本体坐标系的转移矩阵。

测量矢量由角度测量值转换为投影矢量测量值之后，量测噪声v显然处于非线性、非高斯状态，进而导致无法根据测量误差的分布特性准确估计观测噪声的协方差矩阵，致使在该观测方程建立下的滤波方法无法对状态变量进行准确的估计。为此，可以通过引入乘性去偏因子进行模型修正，抑制非线性量测转换带来的模型偏差。

于是，根据以上分析，可以给出观测方程：

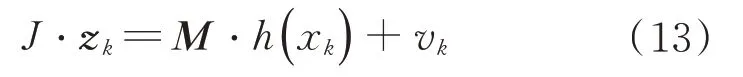
转换测量噪声的方差取为

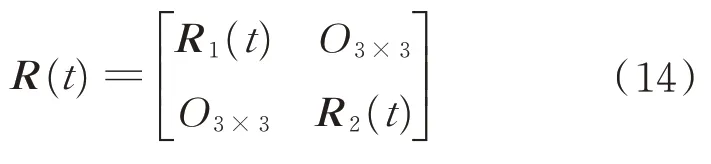
其中，

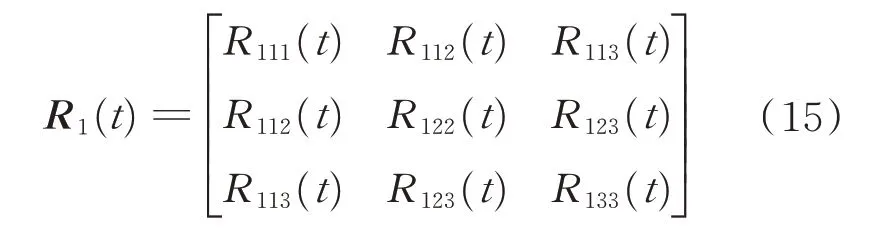
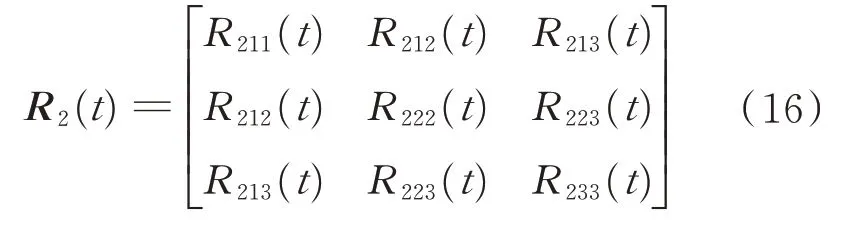
各分量具有如下形式

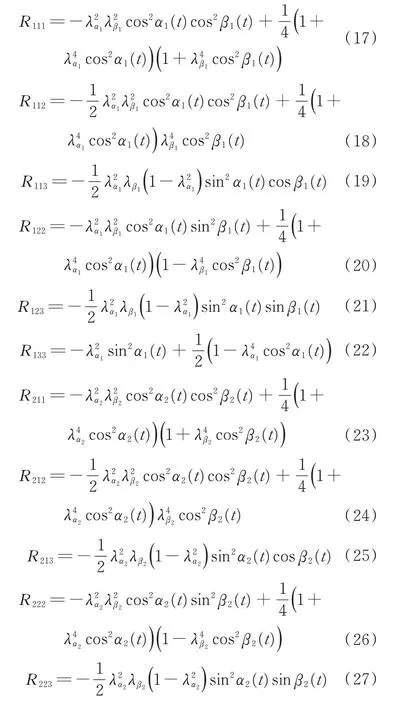
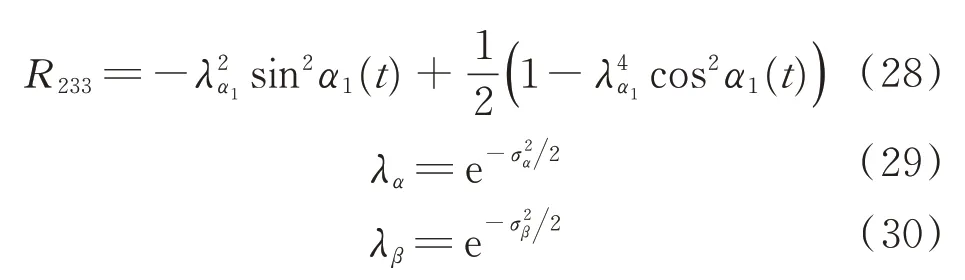
式中：σα、σβ分别为卫星对空间目标观测的方位角和高低角度标准差；J为乘性去偏因子，其表达式为

2 卡尔曼滤波模型

利用扩展卡尔曼滤波对空间目标进行实时状态变量估计，其是一种非常经典的算法，具体算法流程就不展开叙述了。下面根据第1 节建立的动力学方程和观测方程，利用无迹卡尔曼滤波（UKF）方法对空间目标进行实时状态变量估计，具体算法步骤如下：

步骤1

初始化滤波器。设置系统初始状态向量及初始协方差矩阵。

步骤2

最优状态变量估计的sigma 点计算。

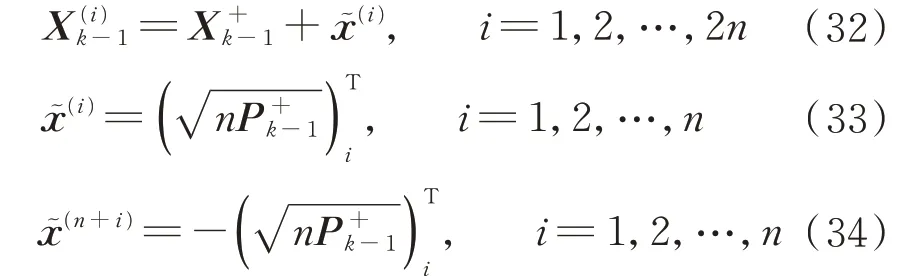
步骤3

状态变量X和协方差矩阵的预测。

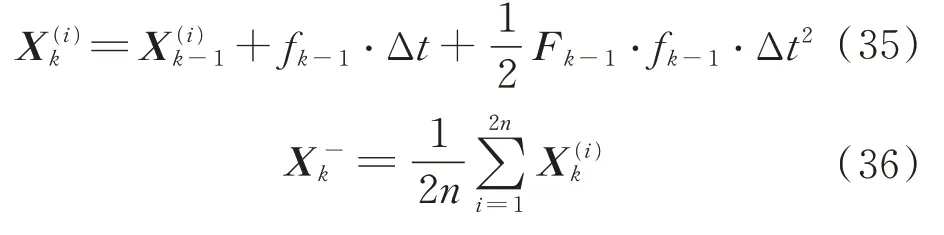
式中：f（X）为系统状态变量X对时间的导数；F（X）为f（X）对系统状态变量的偏导数；Q为系统噪声协方差矩阵。

步骤4

根据状态预测再次计算sigma 点。

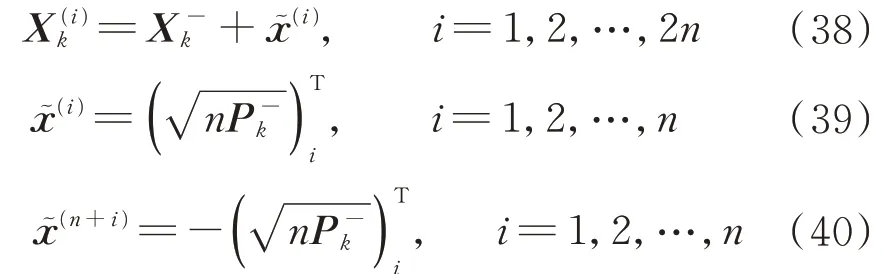
步骤5

观测量z及协方差矩阵的预测。

式中：R为观测噪声协方差矩阵。

步骤6

状态估值与协方差更新。

反复迭代计算，即可实时对目标进行状态变量估计。

3 卡尔曼滤波仿真

空间目标选取星下点轨迹在我国境内由东向西的低轨卫星，依此对双星轨道进行优化设计，使双星在我国上空可以对空间目标进行全程跟踪观测，并且定位误差平均值最小。经过优化计算得出双星及空间目标的轨道六根数见表1。

表1 双星及空间目标的轨道六根数Tab.1 Orbital elements of two satellites and the spatial target

双星与空间目标的轨道位置关系如图2 所示。

图2 双星与空间目标的轨道位置图Fig.2 Diagram of the orbital positions of two satellites and a spatial target

设置双星自身的位置测量误差为30 m（3σ），速度测量误差为0.1 m/s（3σ），姿态测量误差为0.02°（3σ），角度测量误差为0.002°（3σ）。双星的位置、速度、姿态测量误差是根据现有主要卫星的测量误差预估出来的，双星对目标的角度测量误差也是根据现有光学侦察卫星的测角误差预估得出的。

3.1 无迹卡尔曼滤波仿真

根据获取到的观测数据、误差设置及初始条件设置，基于UKF 的空间目标位置估计误差曲线如图3所示。

图3 基于UKF 的空间目标位置估计误差曲线Fig.3 Error curves of the spatial target position estimation based on the UKF

从图3 可以看出：滤波在100 s 后收敛到较为稳定的结果，且300 s 后，空间目标的平均位置估计误差为181.79 m。

3.2 UKF 和EKF 仿 真结果对 比

为了更直观地进行对比，将两种滤波算法对空间目标的位置估计误差曲线放在同一张图中作比较，并给出300 s 后的误差曲线比较，如图4 所示。

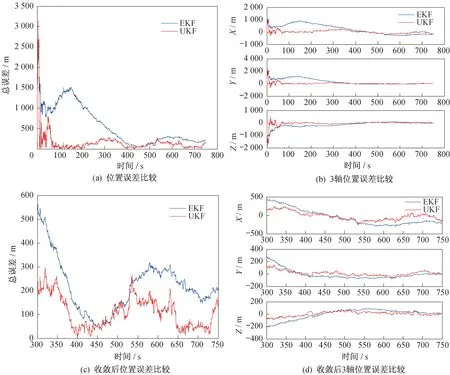
图4 EKF 和UKF 的空间目标位置估计误差曲线比较Fig.4 Comparisons of the error curves of the spatial target position estimations based on the EKF and the UKF

续图4 EKF 和UKF 的空间目标位置估计误差曲线比较Continued fig.4 Comparisons of the error curves of the spatial target position estimations based on the EKF and the UKF

4 结束语

根据上述对EKF 和UKF 动力学法双星定位的仿真结果，可以清楚看出，UKF 动力学法对空间目标位置估计无论在收敛速度上还是在定位精度上均优于EKF 动力学法，其主要原因是无迹卡尔曼滤波算法通过引入了无迹变换，有效地避免了对系统方程的线性化，在加大计算量的同时提高了对空间目标的定位精度。因此，在进行动力学法双星定位时，优先考虑基于无迹卡尔曼滤波的方法。对于空间目标双星定位方法，还需要进一步探索，如增加天基系统中卫星的数目，进一步对整个天基星座进行优化设计，使星座可以对空间中的任意目标进行观测与定位，提高整个天基系统的适用性。