充液挠性航天器姿态机动控制的多目标优化

朱 锐，郭 毓，王 璐，钟晨星

（1.南京理工大学 自动化学院，江苏 南京 210094；2.华为技术有限公司 南京研究所，江苏 南京 210012；3.中国电子科技集团公司第二十九研究所，四川成都 610036）

0 引言

随着空间技术的发展与航天需求的不断增长，现代航天器的飞行任务呈现出多样化趋势，要求航天器既具有长的在轨工作寿命，又能够完成复杂任务［1-2］。这使现代航天器的结构、尺寸日趋复杂与庞大，并且需要携带大量的液体燃料［3-4］，因为液体燃料不但能够满足能量性能要求，而且经济性好、实用性强、燃烧时间长，适用于航天器飞行。此外，为降低发射成本，现代航天器广泛采用轻质附件，如太阳能帆板、大型柔性天线等，这使航天器的挠性越来越大。因此，大型充液挠性航天器已成为未来航天器发展的重要方向之一。

现代航天任务对航天器姿态控制的要求越来越高。例如对地观测卫星，为达到在轨高分辨率跟踪监测的目的，既要求其姿态具有大角度快速机动、快速稳定的能力，又要求具有甚高稳态指向精度与稳定度［5-6］。然而，已有研究发现，充液挠性航天器因携带大量液体燃料和大型轻质挠性附件，其姿态控制系统具有刚-柔-液耦合的复杂非线性动力学特性，姿态机动极易诱发液体晃动和挠性附件振动，这对实现航天器姿态大角度快速机动、快速稳定控制提出了巨大挑战。已有研究发现，路径规划是提高航天器姿态机动性能的关键因素之一，受到了国内外学者的广泛关注。文献［7］在探测器执行空间任务时采用Bang-Coast-Bang（BCB）型路径进行快速机动，但是该路径仍存在因角加速度突变易引起挠性附件振动的问题。文献［8-9］分别提出了S 函数型角速度的机动路径和三段式抛物线型角加速度的机动路径，减少了姿态机动对挠性附件振动的激发。文献［10］提出了一种三段式正弦型角加速度的机动路径，使机动路径更为平滑，进一步提高了姿态机动的快速性和稳态指向精度。文献［11］提出了一种七段式正弦型角加加速度曲线的路径，同时结合模糊多目标粒子群优化算法，对机动路径参数进行优化，可以兼顾多项性能指标，实现挠性航天器快速机动、快速稳定。然而，现有文献大多研究的是刚体或挠性航天器的姿态机动控制问题，研究充液挠性航天器姿态机动路径的文献还很少。

本文针对充液挠性航天器姿态快速机动、快速稳定的控制要求，设计了一种基于正弦型加加速度的七段式姿态机动路径规划方案，结合云多目标粒子群优化算法，联合优化充液挠性航天器的控制器参数和机动路径参数，以减小液体晃动和挠性附件振动对航天器姿态机动控制的影响，提高充液挠性航天器姿态机动的快速性和机动完成后的稳定度。

1 充液挠性航天器动力学模型及姿态控制系统结构

1.1 充液挠性航天器动力学模型

在混合坐标系下，一类带有挠性太阳能帆板及液体燃料的三轴航天器的姿态动力学方程、挠性附件振动方程和液体燃料晃动方程可分别描述为［11］

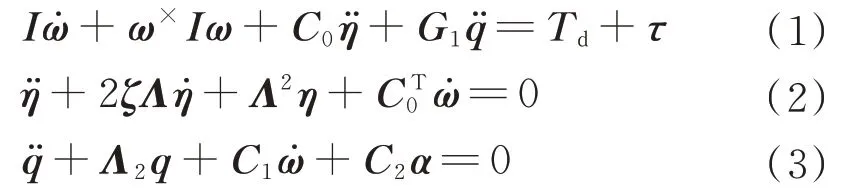
式中：I∈R3×3为航天器转动惯量；ω∈R3×1为航天器本体坐标系相对惯性坐标系的角速度；ω×∈R3×3表示ω的斜对称矩阵；C0∈R3×n为挠性振动与星体姿态运动的耦合系数矩阵；G1∈R3×m、C1∈Rm×3、C2∈Rm×3为液体晃动与星体姿态运动的耦合系数矩阵；τ∈R3×1为控制力矩矢量；Td∈R3×1为环境干扰力矩；ζ∈Rn×n为挠性体 振动模态阻尼比；Λ∈R3×1为挠性体振动模态频率矩阵；Λ2∈Rm×m为液体晃动模态频率平方矩阵；η∈Rn×1为挠性体振动模态矢量；q∈Rm×1为液体晃动模态矢量；α∈R3×1为航天器的姿态角矢量。

1.2 姿态机动路径规划

由于充液挠性航天器具有刚柔液动力学耦合的特点，在进行大角度姿态机动过程中，常常会导致液体的剧烈晃动和挠性帆板的强烈振动，降低了姿态机动的快速性和稳定性。为保证航天器姿态快速机动的同时减少姿态机动对挠性附件振动和液体晃动的激发，需对姿态机动路径进行规划。当前应用较为广泛的是BCB 型路径，采用该路径一定程度上可以改善姿态机动的性能，但由于残余振动较大，机动完成后的指向精度和稳定度难以提高。为提高充液挠性航天器姿态机动控制的性能，本文采用基于正弦型加加速度的七段式路径，对航天器三轴姿态机动路径进行规划。这里以滚动轴为例，说明其具体思路。航天器的角加加速度曲线由正弦函数组成，对其进行三次积分，即得角位置曲线［10］。图1为路径规划示意图。

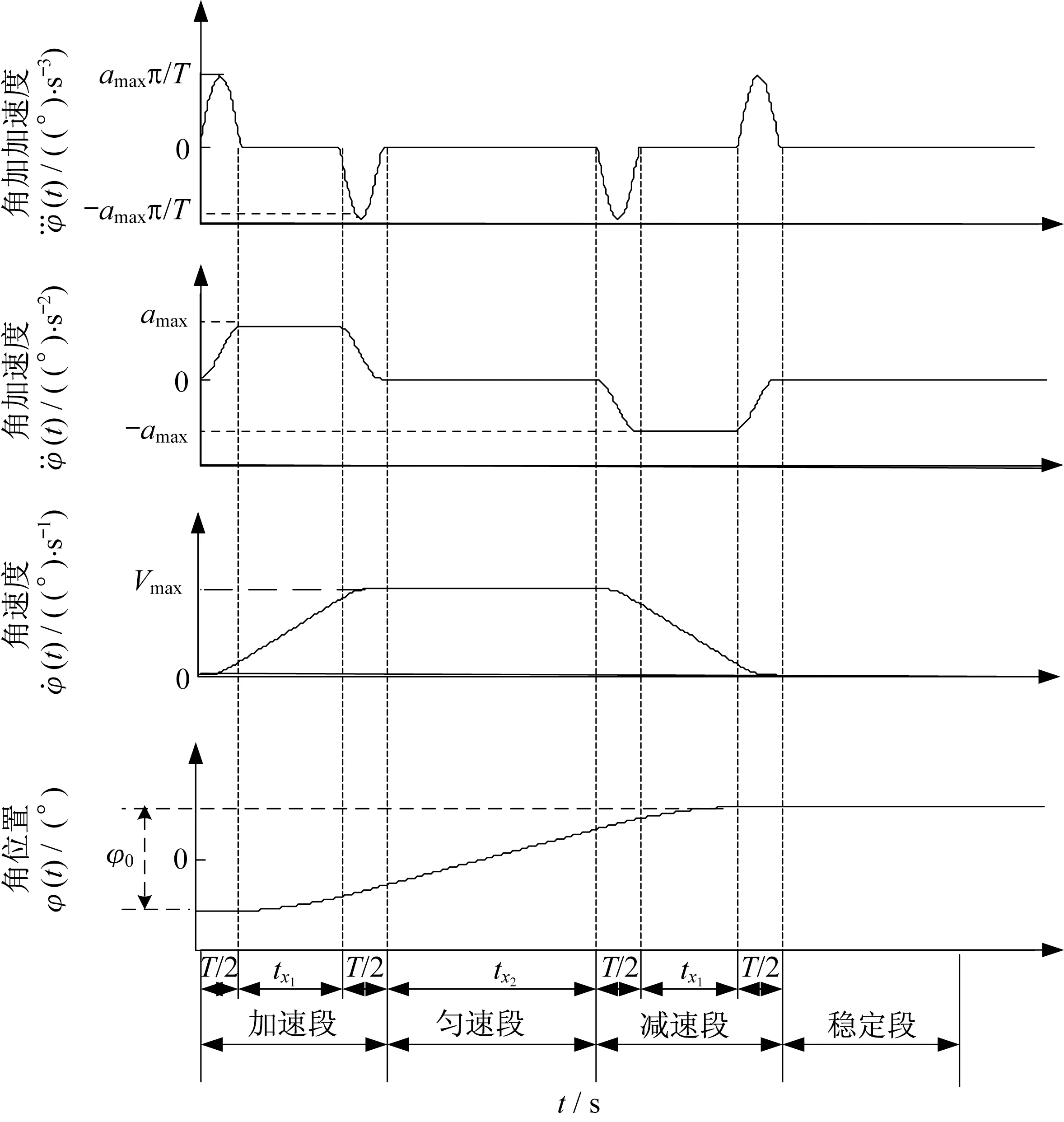
图1 基于正弦型加速度的七段式路径规划示意图Fig.1 The seven-segment path planning diagram based on the sinusoidal acceleration

要求充液挠性航天器的滚动轴从0 机动到φ0，图1中，Vmax和amax分别为航天器滚动轴可达到的最大角速度和角加速度（考虑实际航天器姿态三轴角速度测量元件的测量范围有限，设定Vmax和amax不超过实际系统允许的最大速度Vsystem_max和最大加速度asystem_max），T为正弦函数的周期，tx1为第2 段（匀加速段）和第6 段（匀减速段）的时间，tx2为匀速段的时间。

当航天器姿态机动角度和最大角速度确定后，通过调节角加速度和正弦函数的周期，按照tx1=确定机动路径的参数。七段式机动路径的表达式如下：

第1 段（t≤T/2）

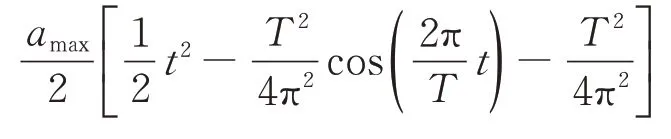
第2 段（T/2 ＜t≤T/2+tx1）

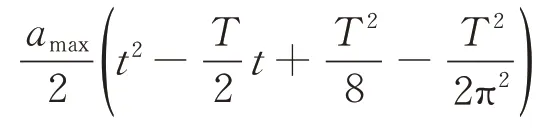
第3 段（T/2+tx1＜t≤T+tx1）

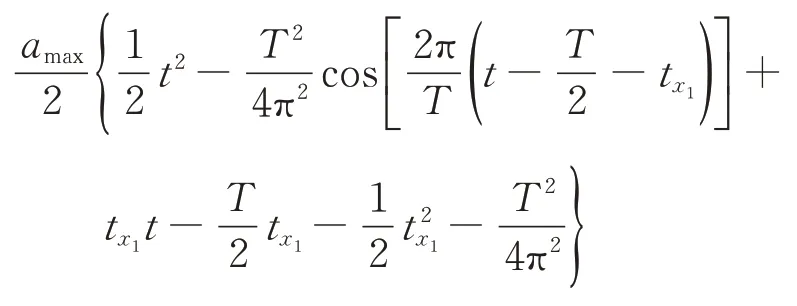
第4 段（T+tx1＜t≤T+tx1+tx2）

第5 段（T+tx1+tx2＜t≤3T/2+tx1+tx2）

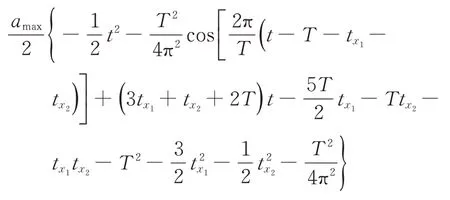
第6段（3T/2+tx1+tx2＜t≤3T/2+2tx1+tx2）

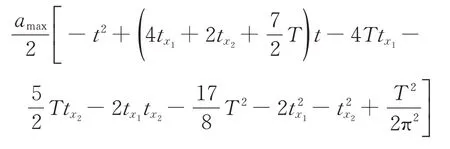
第7段（3T/2+2tx1+tx2＜t≤2T+2tx1+tx2）

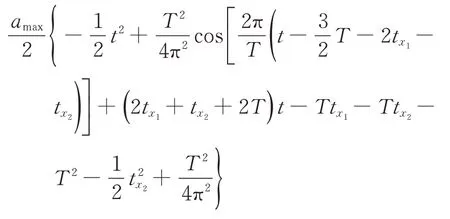
稳定段（t＞2T+2tx1+tx2）

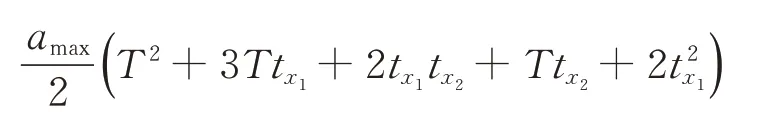
1.3 姿态控制器

为了减小航天器姿态机动对液体晃动和挠性附件振动的激发，实现快速机动、快速稳定的控制目标，采用反馈控制器与机动路径规划相结合的姿态控制方案，系统结构如图2 所示。

图2 充液挠性航天器姿态控制系统结构Fig.2 The structure of the attitude control system for a liquid-filled flexible spacecraft

图2中，αd、分别为期望 的角位置、角加速度向量，α为实际的姿态角向量，e=αd−α为姿态角误差向量。图2中姿态控制器采用微分先行的PD控制律，即

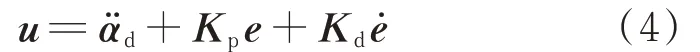
式中：Kp=diag(Kpx，Kpy，Kpz)为姿态控制器的比例控制系数矩阵；Kd=diag(Kdx，Kdy，Kdz)为微分控制系数矩阵；为角速度误差向量。经执行机构输出限幅后，作用到航天器上的控制力矩向量为

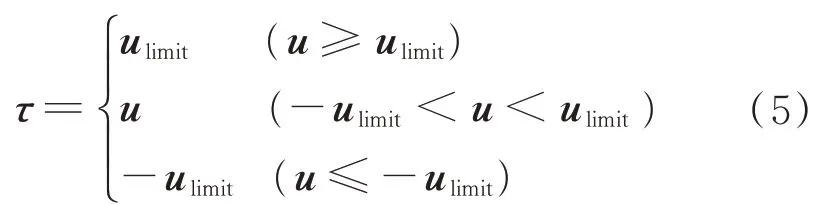
式中：ulimit为执行机构能够输出的最大控制力矩向量。

2 充液挠性航天器姿态机动路径参数及控制器参数联合优化

从航天器动力学模型式（1）～（3）可以看出：由于刚-柔-液耦合特性，航天器大角度姿态机动不仅会激发挠性附件的振动，而且还会激发液体燃料的晃动。同时，挠性附件振动和液体燃料晃动都会影响航天器的姿态控制性能。

航天器大角度姿态机动时，三轴姿态均需满足快速机动、快速稳定的控制目标，但是各项指标之间常常存在矛盾，这是一个复杂的多目标优化问题，需要进行综合优化，使各项指标尽可能好，而不仅仅是某个指标达到最优。此外，由于航天器三轴姿态运动的耦合作用，三轴姿态机动的路径参数及控制器参数均会影响姿态机动的控制性能，如果仅对机动路径参数进行优化，控制器的参数仍然难以选择和优化。针对此问题，本文提出对充液挠性航天器的姿态控制器参数和机动路径参数进行多目标联合优化，以进一步提高姿态机动控制的性能。

云多目标粒子群优化（Cloud Multi-Objective Particle Swarm Optimization，CMOPSO）算法是一种改进的粒子群优化算法，它利用外部粒子群引导群体外粒子的飞行，保存非劣解，利用自适应网格法来维护外部粒子群，从而平衡算法的全局搜索能力和局部搜索能力［12］。CMOPSO 算法具有搜索速度快、效率高、算法简单、能够实现多个目标同时优化等特点，可以较好地解决普通粒子群算法易陷入局部最优的问题，故本文采用CMOPSO 算法对航天器的姿态控制器和路径参数进行联合优化。

充液挠性航天器滚动、俯仰和偏航三轴需优化的姿态机动路径参数分别为三轴机动路径的角加速度的最大值amax_x、amax_y、amax_z和三轴正弦函数的周期Tx、Ty、Tz，需优化的三轴姿态控制器参数为比例系 数Kpx、Kpy、Kpz和微分系 数Kdx、Kdy、Kdz。假 设三轴姿态角达到指定的指向精度pt的时间为f1x、f1y和f1z，三轴稳定度记为f2x、f2y和f2z。姿态机动控制联合优化的目标是使f1x、f1y、f1z、f2x、f2y、f2z同时达到尽可能小的值。为此，建立充液挠性航天器姿态机动路径参数和控制器参数联合优化模型，求取ζ=[amax_y，amax_z，Tx，Ty，Tz，Kpx，Kpy，Kpz，Kdx，Kdy，Kdz]，使得

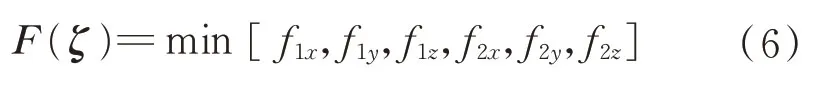
其中，ζ需满足以下约束条件：

1）Kp·∈[Kp·_min，Kp·_max]，其中，Kp·_min、Kp·_max（·=x，y，z，分别代表航天器的滚动轴、俯仰轴以及偏航轴）为设计的航天器三轴姿控器中比例系数的最小值和最大值；

2）Kd·∈[Kd·_min，Kd·_max]，其中，Kd·_min、Kd·_max（·=x，y，z）为设计的航天器三轴姿控器中微分系数的最小值和最大值；

3）amax_·∈(0，amax]（·=x，y，z），其中，amax为规划的姿态机动路径中的最大角加速度的绝对值；

4）设tmax为由姿态机动指标确定的最大机动时间，则 有2T(·)+2t(·)1+t(·)2∈(0，tmax]，(·=x，y，z)，其中，T(·)(·=x，y，z)为三轴机动路径中正弦函数的周期，t(·)1，t(·)2(·=x，y，z)分别为三轴姿态机动路径匀加（减）速段的时间和匀速段的时间；

5）规划的三轴姿态角在t(·)=2T(·)+t(·)1+t(·)2时达到φ(·)0，φ(·)0（·=x，y，z）为设计的航天器三轴的指定机动角度。

在以上限制条件下，联合优化控制器参数和路径参数，得到式（5）的多目标Pareto 解集。CMOP⁃SO 联合优化算法流程如图3 所示。

3 仿真试验及结果分析

3.1 本文算法仿真结果

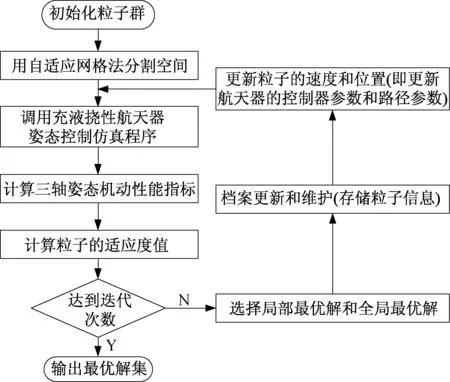
图3 基于CMOPSO 的参数联合优化算法流程图Fig.3 Flow chart of the parameter joint optimization algorithm based on the CMOPSO

仿真用充液挠性航天器的数学模型及参数取自文献［11］。充液挠性航天器初始姿态角为［−30，0.5，0.5］（°），期望达到的姿态角为［30，0，0］（°），三轴初始姿态角速度均为10−3（°）/s。姿态机动采用基于正弦型加加速度七段路径，并利用CMOP⁃SO 联合优化充液挠性航天器姿态机动路径参数和控制器参数。考虑实际航天器姿态三轴角速度测量元件的测量范围有限，设定机动路径的匀速段角速度限幅为Vsystem_max=2.5（°）/s，角加速度限幅为asystem_max=0.4（°）/s2，控制器力矩 限幅为ulimit=25 N·m，系统采样时间为0.05 s。

性能指标：当充液挠性航天器滚动轴机动60°时，考虑三轴运动耦合，为了平稳进行姿态机动，对俯仰轴和偏航轴亦按照所设计的七段路径进行规划，要求三轴姿态机动时间控制在tmax=70 s 之内，指向精度优于pt=0.005°；且在100～150 s（稳定时间）内，稳定度优于6×10−5（°）/s。

本文算法只需运行一次，即可得到多组充液挠性航天器姿控参数联合优化Pareto 解（即优化的路径参数和控制器参数），其中两组Pareto 解见表1。将这两组Pareto 解应用到充液挠性航天器的机动路径和控制器中，对应的姿态机动性能指标见表2。

选取Pareto 解2 用于充液挠性航天器的系统模型中，参数联合优化仿真结果如图4 所示。

由表2 可以看出：充液挠性航天器的控制器参数和机动路径参数经过CMOPSO 联合优化后，得到的这两组Pareto 解都可以使得航天器在49.25 s内完成滚动轴机动60°的机动任务。

表1 基于CMOPSO 算法的姿控参数联合优化Pareto 解Tab.1 The optimized Pareto solutions of joint attitude control parameters based on the CMOPSO

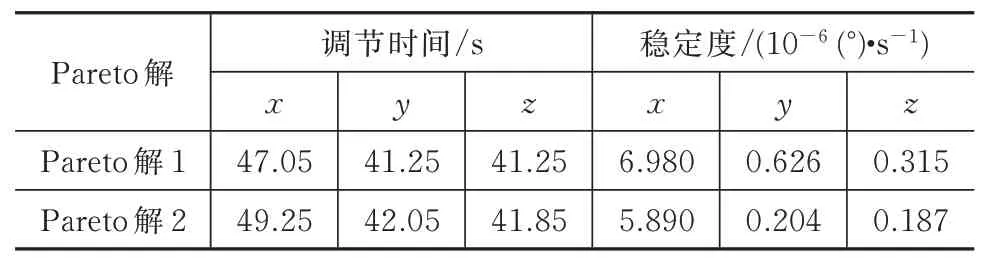
表2 参数优化所得Pareto 解对应的性能指标Tab.2 Performance indexes of the Pareto solutions obtained by the parameter optimization

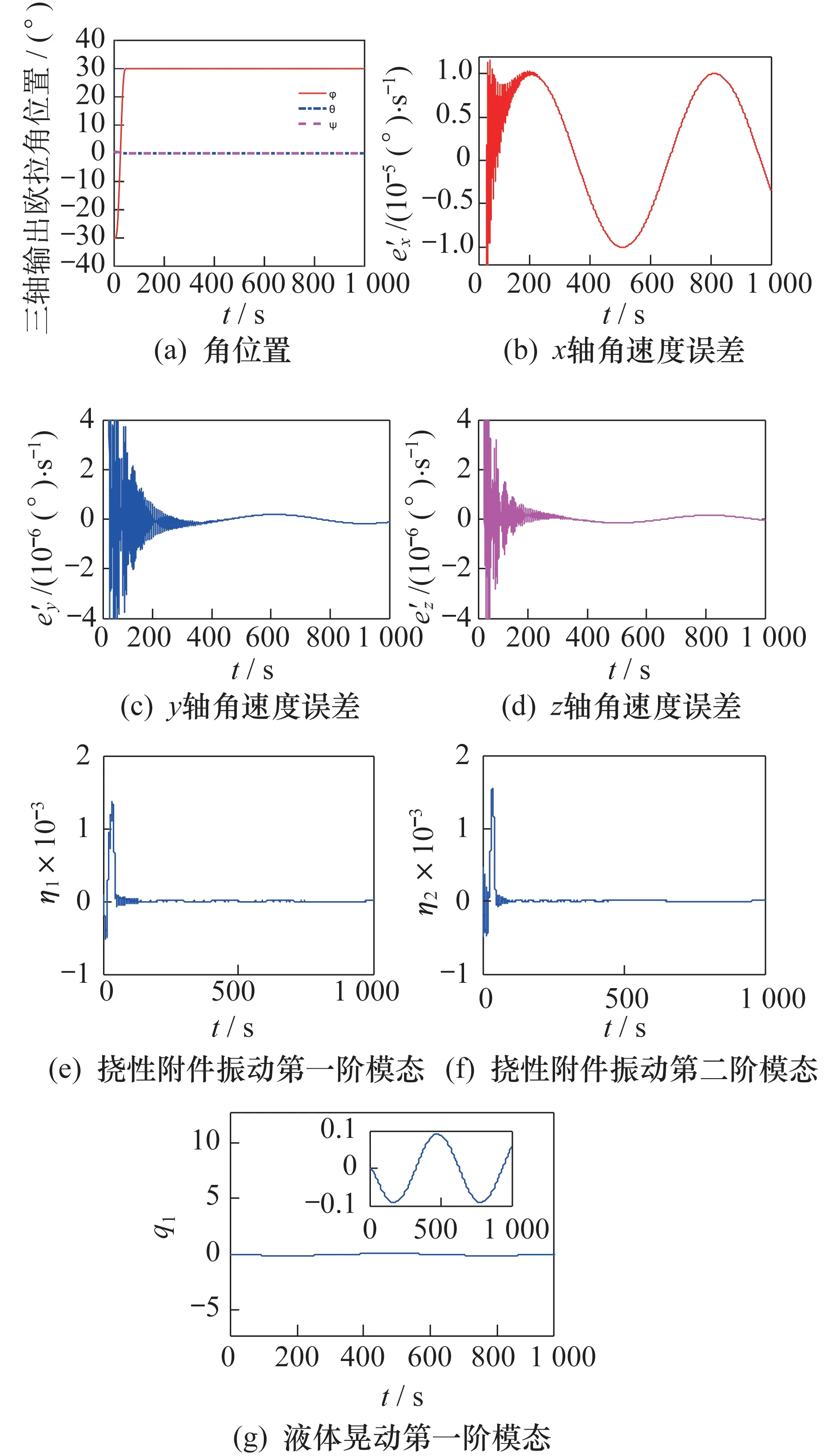
图4 充液挠性航天器参数联合优化仿真结果Fig.4 Simulation results of the joint optimization of parameters for the liquid-filled flexible spacecraft

结合表2 和图4 可以看出：达到稳定状态后，航天器三轴角位置均达到期望的指向精度和稳定度，并且三轴姿态稳定度均可达到10−6（°）/s 的数量级。对比表2中的两组Pareto 解可以看出：Pareto 解1 的调节时间比Pareto 解2 略短，但稳定度较Pareto 解2略低，两组解各有优点，互不支配。由图4（e）、图4（f）可以看出，挠性附件一、二阶振动模态幅值均约为0.001 5。由图4（g）可以看出，液体晃动模态（仅考虑第一阶模态）幅度约为0.1。由此可见，采用本文所提联合优化算法搜索得到的机动路径参数和控制器参数，能使充液挠性航天器完成快速机动、快速稳定的控制目标。

3.2 与其他方法比较

充液挠性航天器在完成大角度姿态机动的任务时，三轴姿态均需满足快速机动、快速稳定的控制目标，并且由于航天器三轴姿态运动的耦合作用，三轴姿态机动的路径参数及控制器参数对姿态机动的控制性能的影响均不容小觑。若只考虑控制器参数对航天器控制性能的影响，不采用本文给出的姿态机动路径规划方法，而直接令滚动轴从初始姿态−30°阶跃至30°，俯仰轴和偏航轴均从初始姿态角度0.5°阶跃至0°，控制器参数采用3.1 节中优化后的Pareto 解2中的控制器参数，获得的航天器姿态机动控制的性能指标如下：三轴调节时间为416.05、419.90、391.50 s，三轴稳定 度为1.450 6、1.519 7、1.380 8（°）/s。姿态阶跃响应仿真结果如图5 所示。

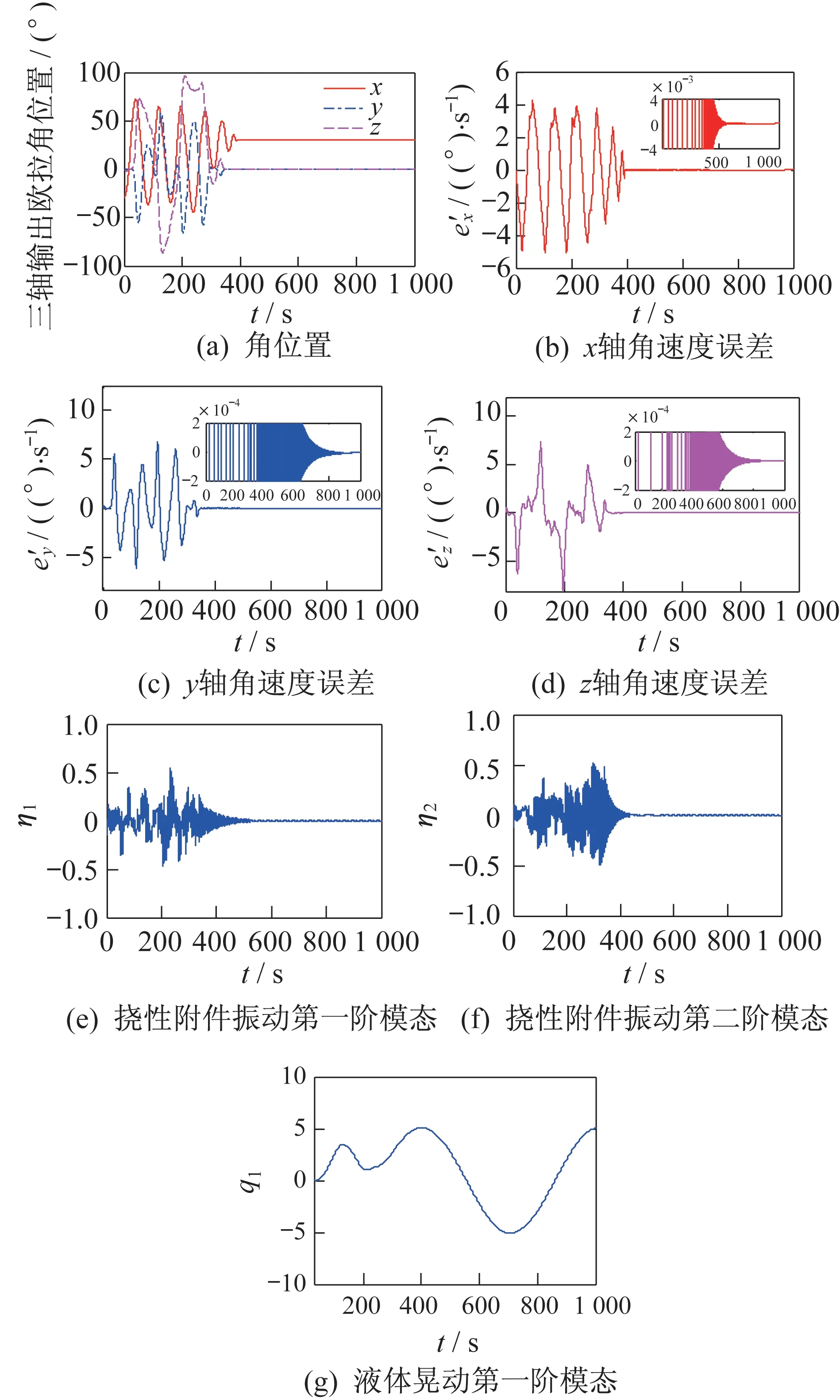
图5 充液挠性航天器姿态阶跃响应仿真结果Fig.5 Simulation results of the attitude step responses of the liquid-filled flexible spacecraft

结合图4 与图5 可看出：采用了联合优化算法获得的姿控参数后，航天器的三轴调节时间缩短了大约360 s，三轴稳定度提高了约10−5倍。总之，采用了联合优化算法获得的姿控参数后姿态机动控制的性能指标均大大优于姿态阶跃机动控制的性能指标。再考虑挠性附件振动强度和液体晃动幅度，对比图4 和图5 可以看出：采用联合优化算法后挠性附件振动第一、二阶模态幅值缩小到原来的1/330，液体晃动第一阶模态幅值缩小到原来的1/60，联合优化算法显著抑制了挠性附件振动和液体晃动。综上，采用了本文设计的联合优化算法搜索得到的机动路径参数和控制器参数后，航天器的姿态控制性能均有较大提高，并且挠性附件振动和液体晃动亦得到非常有效的抑制，从而验证了联合优化算法的有效性。

4 结束语

本文针对一类带液体燃料和挠性附件的航天器快速机动、快速稳定的控制要求，研究了一种姿态机动路径优化方法，将微分先行的PD 姿态控制器与基于正弦型加加速度的七段路径规划相结合，并采用CMOPSO 算法联合优化充液挠性航天器姿态控制器参数及机动路径参数。仿真结果表明：采用本文所提联合优化算法的姿控参数能够显著减小液体晃动和帆板振动对航天器的影响，使充液挠性航天器能够较好地完成大角度姿态快速机动、快速稳定的任务。目前本文在姿态机动角度已知的情况下，研究了航天器姿态机动路径及参数优化的问题，由于计算量较大，只能离线优化。未来将进一步研究更为有效的在线优化方法，从而实时规划航天器机动路径，以适应更为复杂的航天任务要求。