垂直轴风力机两种翼型气动性能比较研究

汪 泉，陈晓田，黄 攀，甘 笛，曾利磊，胡梦杰

（湖北工业大学 机械工程学院，湖北 武汉 430068）

0 前言

风能作为一种无污染、 无危害并且储量十分丰富的可再生能源，越来越受到各国学者的青睐。与水平轴风力机相比，H 型垂直轴风力机结构简单，不须要设置偏航装置，发电机安装在塔底，便于安装和维修，而且叶片的制造过程简单，不需要较高的成本[1]。

近年来研究人员对H 型垂直轴风力机的叶片进行了针对性研究。 Ning Ma[2]基于遗传算法对NACA0018 翼型进行优化，CFD 仿真结果显示：当叶尖速比（λ）为0.9 时，较优化前风力机功率系数（Cp）提高了 26.82%。Changping Liang[3]采用类函数和形状函数变参数优化方法对NACA0015 翼型几何形状进行扰动，最大升力系数、最大升阻比和最大切向力系数 （CT） 分别提高 7.5%，9%和8.87%。 梁昌平[4]利用CST 参数化方法对NACA0015翼型几何外形进行扰动，基于非支配排序的遗传算法进行几何优化，优化后的翼型最大升力系数提高 6.63%，最大 CT 提高 22.7%。 Carlos Simão Ferreira[5]推导垂直轴风力机翼型气动优化公式，并验证了优化公式的有效性。

上述研究主要以对称翼型为研究对象，而对非对称翼型的垂直轴风力机研究颇少[6]。 叶片作为风力机最重要的组成部分，是捕获风能的重要部件[7]。 在不同的风能资源情况下，翼型的选择对提高H 型垂直轴风力机的风能利用率有着重要的作用。 本文基于 NACA0018，NACA4418 翼型，以风力机的Cp和单个叶片的CT 作为判断依据，建立垂直轴风力机模型并进行CFD 仿真，对比分析在不同的λ 下两种风力机模型的气动特性。

1 CFD模型建立

1.1 几何模型与边界条件设置

NACA0018 和 NACA4418 翼型如图 1 所示。

图 1 NACA0018 和 NACA4418 翼型Fig.1 NACA0018 airfoil and NACA4418 airfoil

本文中两种翼型的弦长均为0.1 m。两种垂直轴风力机模型的主要参数如表1 所示。

表1 风力机模型参数Table 1 Model parameters of wind turbine

连杆作为风力机的一部分，同样受到空气阻力。当连杆的直径很小时，对风力机的功率转换影响微乎其微，故模型中省略连杆。

图2 所示的简化几何模型与实验模型相似[8]。矩形的DE 边为速度入口，入口边界条件设为速度入口，速度大小为4.1 m/s，方向从左到右。 出口边界为矩形的FG 边，出口边界条件设为压力出口，为标准大气压。矩形计算域的上下边界条件设为对称。 图2 中的 C 区域为静止区域，A 和 B 区域为旋转区域，不同区域之间的交界面设为interface。 旋转区域的滑移网格运动方式设为moving mesh。 翼型壁面设为无滑移壁面条件。

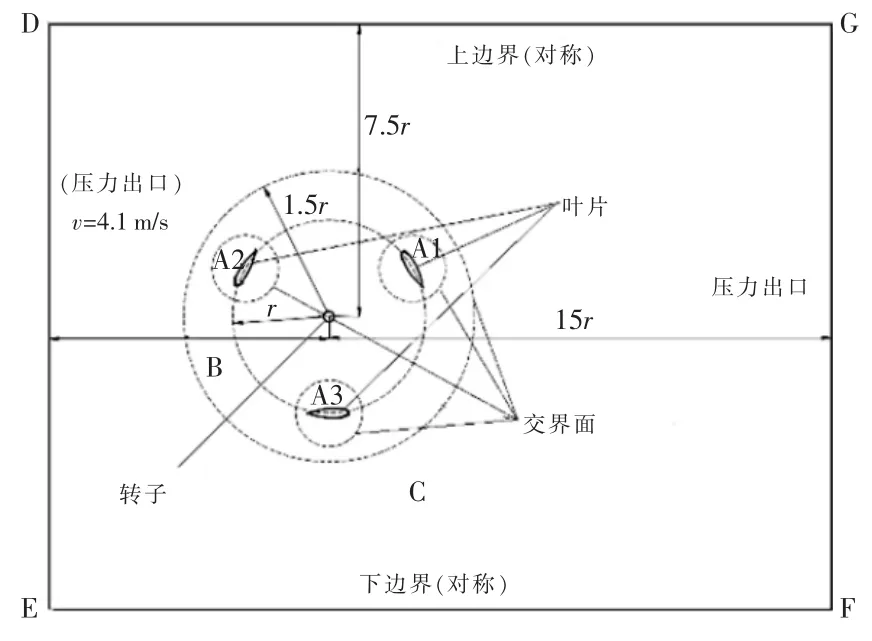
图2 CFD 计算模型Fig.2 Computational model of CFD

1.2 网格划分与计算模型时间步长设置

对于CFD 分析，一般网格划分占整个前处理周期的80%，网格的质量对计算结果和计算精度有很大的影响。 结构化网格的质量要高于非结构网格的质量，计算精度和计算效率都比非结构化网格好。为保证仿真结果的准确性，本文网格划分均采用结构化网格，采用CFD 前处理工具ICEM进行网格划分，网格划分如图3 所示。

图3 网格划分Fig.3 Mesh generation

以NACA0018 翼型建立的二维模型网格数量为470 258，节点数为 466 585。 以翼型 NACA4418建立的二维模型网格数量为563 138，节点数为559 465。 由于近翼型壁面处的流场复杂，考虑叶片近壁面处网格质量对计算结果有影响，临近翼型壁面处的网格均加密处理。

为了保证计算结果的精度和可信度，本文对H 型垂直轴风力机的研究采用Fluent 滑移网格技术。 时间步长的选择关系到计算的效率和结果的准确性。 在Fluent 软件中预先设置计算的时间步数和时间步长。 时间步长越小，计算精度就越高，反之计算精度就越低。 在设定好一个时间步长内风力机旋转的度数后，得到风力机在旋转一个周期内的步数（K）和旋转 n 度的时间步长（t）。

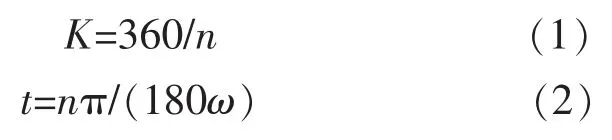
式中：ω 为风力机转速。

1.3 湍流模型

Fluent 提供的湍流模型很多，每一种湍流模型的适用情形都各不相同。 单方程Spalart-Allmaras 适用于不是特别复杂压力梯度作用下的边界层流动。两方程主要有k-epslion 和k-omega 两种湍流模型。标准的k-epslion 湍流模型具有较好的通用性，但遇到旋涡以及逆压梯度问题时，计算精度较低。 k-omega 湍流模型能较好地解决边界层、自由剪切的问题。特别是SST k-omega 模型适用于逆压梯度下复杂边界层流动及分离。 梅毅[9]分别用RNG k-epslion 模型、Realizable k-epslion模型和SST k-omega 模型进行垂直轴风力机的数值模拟，结果表明SST k-omega 模型计算得到的功率系数更接近实验值。综上所述，基于本文中建立的垂直轴风力机二维流场模型为瞬态，且风轮附近流场较复杂，故选择SST k-omega 湍流模型。

1.4 求解器设置

Fluent 软件中提供了压力基求解器和密度基求解器两种求解方式。 本文选择压力基求解器。SIMPLE 算法和SIMPLEC 算法都适用于大多数不可压缩流动的工程问题，但SIMPLEC 算法在四边形网格的计算中更准确，收敛速度更快，故采用SIMPLEC 算法。 压力、动量和其他变量分别采用二阶逆风、有界中心差分和三阶MUSCL 格式，各项残差为0.000 01。

2 计算结果处理方法

在Fluent 仿真模拟中，监测到的图像为风力机旋转过程中的力矩系数曲线，力矩系数输出值的处理很重要。 在仿真模拟的前几个周期由于风力机处于非稳定状态，监测到的力矩系数曲线杂乱无章[9]。 待风力机稳定后，力矩系数曲线呈周期性变化。为保证计算结果的准确性，待风力机处于稳定状态过后，取最后一个周期的力矩系数数据进行分析。 由Fluent 仿真模拟中输出的力矩系数求得扭矩（T）。

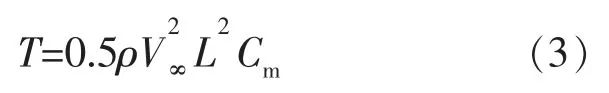
式中：ρ 为空气密度，g/m3；V∞为来流风速，m/s；L为叶片弦长，m；Cm为力矩系数。

由扭矩可以求得风能利用系数（Cp）。

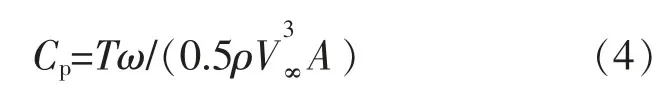
式中：A 为风力机扫风面积，m2。

3 结果与分析

3.1 仿真结果验证

以模型1 为例，与风洞实验中建立的模型相似。利用风洞实验结果与CFD 仿真模拟结果作对比，验证CFD 仿真结果的正确性。 图4 为风洞实验与CFD 仿真在不同λ 下垂直轴风力机的Cp。由图4 可知，CFD 仿真结果较好地显示了Cp的变化趋势。 在低λ 范围内，风洞实验与CFD 仿真结果基本一致。 在高λ 范围内，CFD 仿真模拟低估了H 型垂直轴风力机的Cp，但仿真结果在可接受的误差范围内。 从Cp整体的变化趋势来看，CFD仿真模拟与风洞实验结果有较好的吻合性。

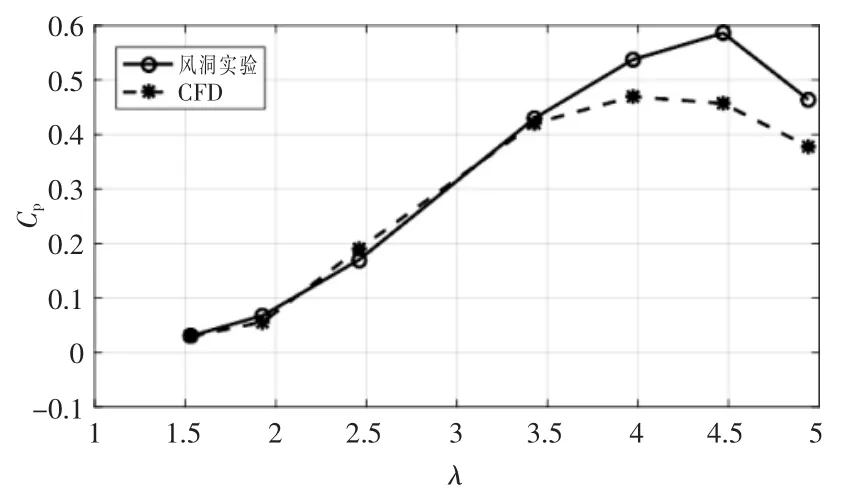
图4 风洞实验与CFD 仿真模拟在不同λ 下的功率系数Fig.4 Power coefficient of numerical simulation and wind tunnel test at different tip seed ratio

3.2 风能利用率

图5 不同λ 下的CpFig.5 Power coefficient at different tip seed ratio

取风力机仿真结果中最后一个周期的力矩系数的平均值，根据式（1），（2）求出风力机的 Cp。 图5 为两种模型在不同 λ 下的 Cp。由图5 可知，两种模型在不同λ 下的Cp曲线变化趋势大致相同。当风力机在低速状态（低λ）下运行时，风力机Cp较低。 因为风力机在低速状态下运行时，叶片多数处于失速状态，产生的气动力较小，因此，风力机气动特性较差。 当风力机在高速状态（高λ）下运行时，风力机Cp随转速增加而降低，因为高速状态时，风轮局部气流受到破坏，导致风力机气动特性差。 当风力机在最佳λ 状态运行时，风力机具有良好的气动性能，Cp达到最大值。 此外，在低 λ 时，NACA448 翼型的风力机 Cp较 NACA0018翼型的风力机高；相反，在高 λ 时，NACA0018 翼型的风力机Cp高。说明NACA4418 翼型风力机在低速状态下的气动特性好，适用于低风速地区。而NACA0018 翼型风力机在高速状态下的气动特性好，适用于高风速地区。

3.3 不同λ下翼型的CT分析

取风力机最后一个周期的单个叶片的切向力计算结果作为分析对象。 图6 为单个翼型在低λ下的 CT 变化曲线。 由图6 可知： 在低的 λ 范围内，由于整个风力机处于失速状态，叶片受到失速气流的干扰，导致CT 曲线波动杂乱无章；在整个方位角范围内，NACA0018 翼型CT 曲线波动范围比NACA4418 翼型大；在方位角180°附近，当λ为 1.53，1.93 和 2.46 时，NACA4418 翼型 CT 大得多；当 λ 为 1.53 和 1.93 时，在方位角 300 °附近，NACA0018 翼型的负CT 值同样比NACA0018 翼型大得多。 这也是在低λ 时NACA4418 翼型风力机风能利用率较NACA0018 翼型的高的原因。 由此可知，相比较 NACA0018 翼型，NACA4418 翼型在低风速下有更好的气动性能。

图6 单个叶片在低λ 下的CT 曲线Fig.6 Tangential force coefficient curves of single blade at low tip speed ratio

图7 为单个 NACA0018 与 NACA4418 翼型在高λ 下CT 变化曲线。

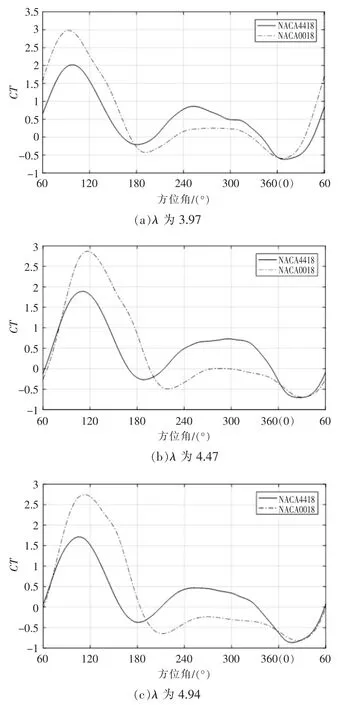
图7 高λ 下单个叶片的CT 曲线Fig.7 Tangential force coefficient curves of single blade at low tip speed ratio

由图7 可知，NACA0018 与 NACA4418 翼型CT 曲线变化趋势相同。随着λ 的增大，翼型CT曲线下移，风力机Cp随着转速的增加逐渐降低，说明翼型在高λ 下，叶片的气动力下降。 翼型方位角在 0～180 °时，NACA0018 与 NACA4418 翼型CT曲线的波峰值随着转速的增加差值增大，且NACA0018 翼型的CT 平均值高于 NACA4418 翼型，说明NACA0018 翼型在上风区气动性能较NACA4418 翼型好。 而翼型在方位角为180～360°时，翼型CT 随着λ 的增加向纵轴负方向移动，但NACA4418 翼型 CT 曲线大部分在 NACA0018 翼型的上方，且NACA4418 翼型的CT 平均值高于NACA0018 翼型，说明 NACA4418 翼型在下风区的气动性能较NACA0018 翼型好。

4 结论

本文通过对垂直轴风力机两种翼型气动特性的比较研究，得到以下结论。

①当垂直轴风力机翼型为NACA4418 翼型，在低λ 的情况下运行时，风力机的气动特性要优于 NACA0018 翼型的风力机。 相反，在高的 λ 时，NACA0018 翼型风力机的气动特性好。 因此，NACA4418 翼型适用于低风速区域，而NACA0018 翼型适用于高风速区域。

②风力机在高λ 时：NACA0018 翼型在上风区的CT 平均值高于NACA4418 翼型；在下风区，NACA4418 翼型的 CT 平均值高于 NACA0018 翼型。说明高λ 时，NACA0018 翼型在上风区的气动性能比NACA4418 翼型好，在下风区NACA4418翼型气动性能好。